Ubungen zur Physik 2 – Blatt 3

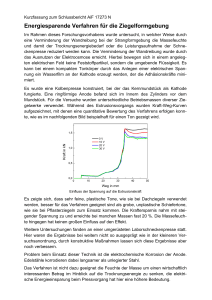
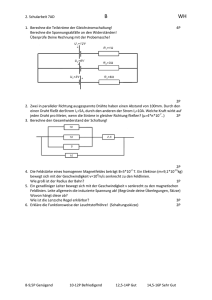
Prof. T. Esslinger
Dr. T. Donner
Dr. F. Brennecke
Übungen zur Physik 2 – Blatt 3
∗
(Abgabetermin: Montag, 18. März 2013, 8:30 Uhr, Briefkästen der Assistenten im Foyer HPF (D-Stock))
I.
VORDIPLOMÜBUNGSAUFGABE: KATHODENSTRAHLRÖHRE (3 PUNKTE)
Eine Kathodenstrahlröhre – wie sie zum Beispiel in alten Fernsehern, Computermonitoren oder Oszilloskopen
eingebaut ist – basiert auf der elektrostatischen Ablenkung eines Elektronenstrahls. Elektronen aus einer geheizten
Kathode werden in Richtung der Anode auf eine Geschwindigkeit von v = 1.3 × 107 m/s beschleunigt und durchﬂiegen
anschliessend ein gleichförmiges elektrisches Feld der Grösse E = 1500 V/m, welches durch zwei geladene, parallele
Platten erzeugt wird. Dabei werden die einzelnen Elektronen im elektrischen Feld abgelenkt und treﬀen nach einer
weiteren Flugstrecke auf den Schirm S.
S
UB
e-
x
Heizung
Kathode
Anode
l = 6cm
L = 12cm
1. Welche Beschleunigungsspannung UB zwischen Kathode und Anode durchlaufen die Elektronen?
2. Wie gross ist die Kraft auf ein Elektron, wenn es sich zwischen den Platten beﬁndet und in welche Richtung
zeigt sie?
3. Um welche Strecke ∆x1 ist das Elektron abgelenkt worden, wenn es das elektrische Feld verlässt?
4. In welchem Abstand ∆x2 von der ursprünglichen Flugbahn entfernt triﬀt es auf den Schirm?
II.
ELEKTRISCHES FELD (3 PUNKTE)
Berechne das elektrische Feld einer sphärisch symmetrischen Ladungsverteilung mit Gesamtladung Q, deren Ladungsdichte folgendermassen gegeben ist: ρ(r) = ρ0 (1 − r/R) für r ≤ R und ρ(r) = 0 für r > R. Wie gross ist ρ0 ? Wo
ist das elektrische Feld maximal? Skizziere den Verlauf der elektrischen Feldstärke E(r) als Funktion des Abstandes
r.
III.
WASSERMOLEKÜL: DIPOL IM INHOMOGENEN ELEKTRISCHEN FELD (4 PUNKTE)
1. Ein Wassermolekül hat ein vergleichsweise grosses permanentes elektrisches Dipolmoment von p = 6.17 ×
10−30 Cm. Wir nehmen an, dass dieses Dipolmoment durch zwei Punktteilchen mit Abstand d und Ladungen e und −e gebildet wird. Berechne den Abstand d.
∗ Aufgaben
und Lösungen sind auch erhältlich unter www.quantumoptics.ethz.ch → Lectures
2
2. Ein Wassermolekül beﬁnde sich in der Nähe eines unendlich langen Drahtes, der mit der Linienladungsdichte
1 2λ
λ positiv geladen ist. Das resultierende elektrische Feld des Drahtes hat dann den Betrag E = 4πϵ
, wobei
0 r
⃗
r der Abstand zum Draht ist (siehe Skizze). Bestimme den Vektor E(r, α) des elektrischen Feldes als Funktion
y
p
β
r
Draht
α
x
von r und α. Betrachte einen Dipol, der fest an einer beliebigen Position im elektrischen Feld des Drahtes sitzt.
Wie hängt seine potentielle Energie von den beiden Winkeln α und β ab? Für welche Winkel α, β wird die
potentielle Energie minimiert?
3. Sei das Wassermolekül nun in r = 1.5 cm Entfernung vom Draht auf der x-Achse positioniert und entlang der
x-Achse ausgerichtet. Berechne die Beschleunigung des Moleküls in x-Richtung für λ = 1 × 10−9 C/m. Benutze
dabei das Ergebnis von Aufgabenteil 1.
4. Was passiert wenn man einen positiv geladenen Draht in die Nähe eines Wasserstrahls hält? Der Strahl wird a)
angezogen, b) abgestossen oder c) fällt unbeirrt weiter. Begründe Deine Antwort mit Hilfe der obigen Ergebnisse.
Ändert sich das Ergebnis wenn der Draht negativ geladen ist?