Kurze Wege auf dem Geobrett führen zum Pascal

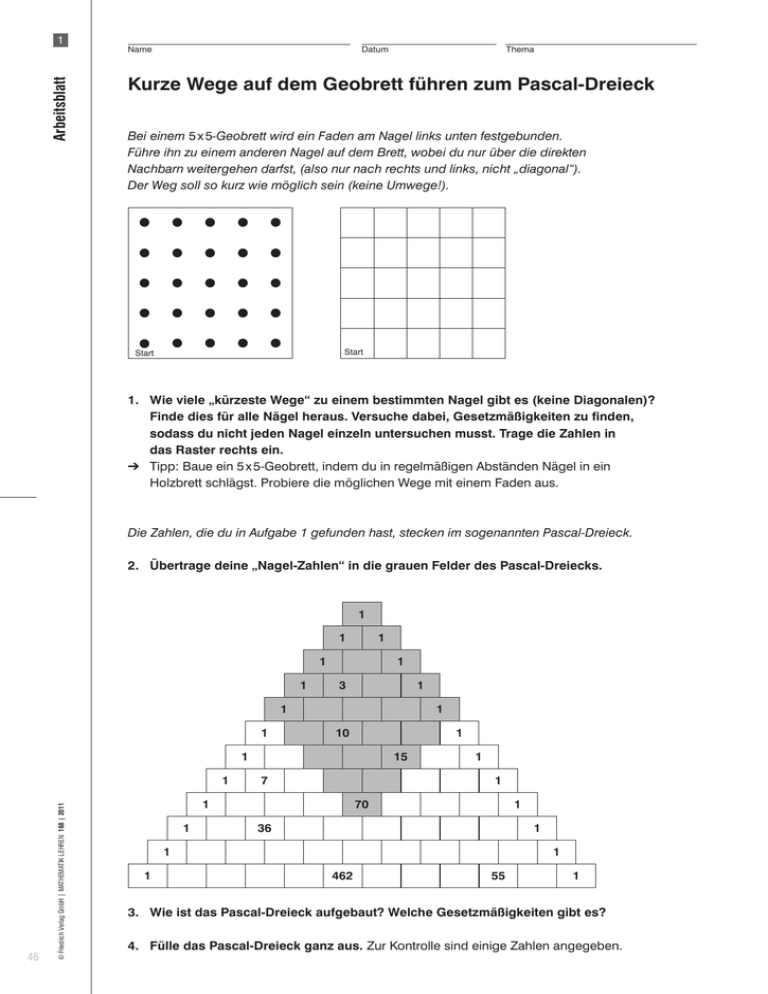
Arbeitsblatt
1
Name
Datum
Thema
Kurze Wege auf dem Geobrett führen zum Pascal-Dreieck
Bei einem 5 x 5-Geobrett wird ein Faden am Nagel links unten festgebunden.
Führe ihn zu einem anderen Nagel auf dem Brett, wobei du nur über die direkten
Nachbarn weitergehen darfst, (also nur nach rechts und links, nicht „diagonal“).
Der Weg soll so kurz wie möglich sein (keine Umwege!).
•
•
•
•
•
Start
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Start
1. Wie viele „kürzeste Wege“ zu einem bestimmten Nagel gibt es (keine Diagonalen)?
Finde dies für alle Nägel heraus. Versuche dabei, Gesetzmäßigkeiten zu finden,
sodass du nicht jeden Nagel einzeln untersuchen musst. Trage die Zahlen in
das Raster rechts ein.
➔ Tipp: Baue ein 5 x 5-Geobrett, indem du in regelmäßigen Abständen Nägel in ein
Holzbrett schlägst. Probiere die möglichen Wege mit einem Faden aus.
Die Zahlen, die du in Aufgabe 1 gefunden hast, stecken im sogenannten Pascal-Dreieck.
2. Übertrage deine „Nagel-Zahlen“ in die grauen Felder des Pascal-Dreiecks.
1
1
1
1
1
1
3
1
1
1
1
10
1
1
46
© Friedrich Verlag GmbH | Mathematik lehren 168 | 2011
1
15
7
1
1
1
1
70
1
36
1
1
1
1
462
55
1
3. Wie ist das Pascal-Dreieck aufgebaut? Welche Gesetzmäßigkeiten gibt es?
4. Fülle das Pascal-Dreieck ganz aus. Zur Kontrolle sind einige Zahlen angegeben.
Arbeitsblatt
5
Name
Datum
Thema
Vielfache und Brüche im Pascal-Dreieck
1. Suche benachbarte Zahlen im Pascal-Dreieck, die (ganzzahlige) Vielfache sind.
Arbeite von links nach rechts. Suche Zahlen, die ein Vielfaches der Zahl links neben
ihr sind. Findest du ein Muster?
➔ Tipp: Untersuche die schrägen Reihen.
2. Schreibe in die Kreise die Zahl, mit der du die linke Zahl malnehmen musst,
um die rechte Zahl zu erhalten. Oft ist dies eine Bruchzahl.
1
1
1
1
1
1
1
5
6
8
3
10
21
28
1
6
15
7
1
3
4
1
1
2
5
10
20
35
56
1
1
5
15
35
70
1
6
21
56
1
7
28
1
8
1
3. Untersuche die siebte Zeile im Pascal-Dreieck:
1
___
6
___
15
___
20
___
15
___
6
___
1
47
© Friedrich Verlag GmbH | Mathematik lehren 168 | 2011
a) Mit welcher Zahl muss jeweils multipliziert werden, um von einer Zahl zur nächsten Zahl zu kommen? Schreibe sie auf die Linien.
b) Welches Muster steckt in den Brüchen?
c) Gilt das Muster auch in den anderen Zeilen des Pascal-Dreiecks? Überprüfe dies
in der Zeile darüber und darunter. Dabei musst du manchmal geschickt erweitern.
d) Was musst du rechnen, um die 5. Zahl in der 7. Zeile zu finden?
e) Wie findest du die 3. Zahl in der 10. Zeile? Und wie die 6. Zahl in der 12. Zeile?
f) Schreibe eine Regel auf, mit der du die Zahlen im Pascal-Dreieck berechnen
kannst.
48
1
1
15
1
14
1
105
13
91
12
455
78
11
220
45
36
330
3003
84
21
56
15
462
126
70
20
6
462
126
35
10
3
330
84
21
5
1
495
36
7
1
220
45
8
1
3003
55
9
1
286
66
10
1
364
1365
1001
715
165
2002
5005
3003
28
6
1
120
1287
792
6435
3432
56
15
4
1
210
1716
924
252
6435
3003
5005
35
10
1716
792
210
1287
495
120
28
2002
715
165
1001
286
55
1365
364
66
10
9
8
7
6
5
4
3
2
1
455
78
11
1
91
12
1
105
13
1
14
1
15
1
1
1
Datum
1
1
1
1
1
1
1
1
1
1
Arbeitsblatt
Name
1
© Friedrich Verlag GmbH | Mathematik lehren 168 | 2011
1
Thema
49
1
9
8
36
7
28
6
84
21
5
56
15
4
126
35
10
3
70
20
6
2
126
35
10
3
1
56
15
4
1
84
21
5
1
28
6
1
36
7
1
8
1
9
1
1
1
Datum
1
1
1
1
1
1
1
Arbeitsblatt
Name
1
© Friedrich Verlag GmbH | Mathematik lehren 168 | 2011
1
Thema