Lösungen zur Abiturprüfung 2001 Physik

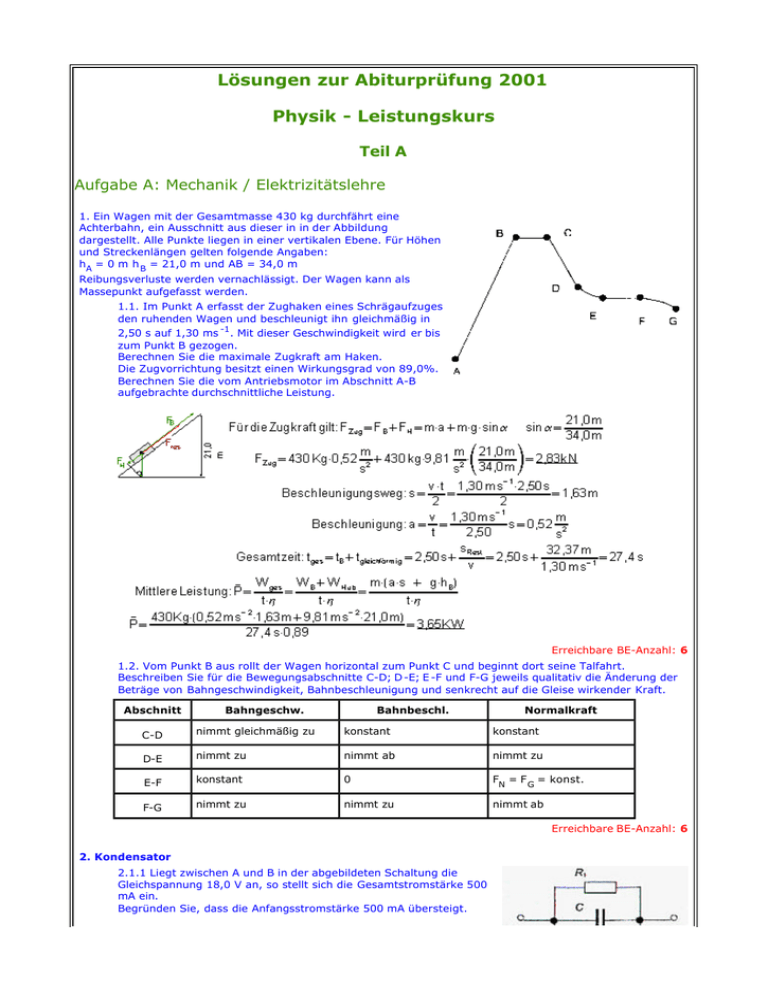
Lösungen zur Abiturprüfung 2001
Physik - Leistungskurs
Teil A
Aufgabe A: Mechanik / Elektrizitätslehre
1. Ein Wagen mit der Gesamtmasse 430 kg durchfährt eine
Achterbahn, ein Ausschnitt aus dieser in in der Abbildung
dargestellt. Alle Punkte liegen in einer vertikalen Ebene. Für Höhen
und Streckenlängen gelten folgende Angaben:
hA = 0 m h B = 21,0 m und AB = 34,0 m
Reibungsverluste werden vernachlässigt. Der Wagen kann als
Massepunkt aufgefasst werden.
1.1. Im Punkt A erfasst der Zughaken eines Schrägaufzuges
den ruhenden Wagen und beschleunigt ihn gleichmäßig in
2,50 s auf 1,30 ms -1. Mit dieser Geschwindigkeit wird er bis
zum Punkt B gezogen.
Berechnen Sie die maximale Zugkraft am Haken.
Die Zugvorrichtung besitzt einen Wirkungsgrad von 89,0%.
Berechnen Sie die vom Antriebsmotor im Abschnitt A-B
aufgebrachte durchschnittliche Leistung.
Erreichbare BE-Anzahl: 6
1.2. Vom Punkt B aus rollt der Wagen horizontal zum Punkt C und beginnt dort seine Talfahrt.
Beschreiben Sie für die Bewegungsabschnitte C-D; D -E; E -F und F-G jeweils qualitativ die Änderung der
Beträge von Bahngeschwindigkeit, Bahnbeschleunigung und senkrecht auf die Gleise wirkender Kraft.
Abschnitt
Bahngeschw.
Bahnbeschl.
Normalkraft
C-D
nimmt gleichmäßig zu
konstant
konstant
D-E
nimmt zu
nimmt ab
nimmt zu
E-F
konstant
0
FN = F G = konst.
F-G
nimmt zu
nimmt zu
nimmt ab
Erreichbare BE-Anzahl: 6
2. Kondensator
2.1.1 Liegt zwischen A und B in der abgebildeten Schaltung die
Gleichspannung 18,0 V an, so stellt sich die Gesamtstromstärke 500
mA ein.
Begründen Sie, dass die Anfangsstromstärke 500 mA übersteigt.
Berechnen Sie den Widerstand R 1 des ohmschen Bauelementes.
Beim Einschalten kommt es kurzzeitig zum Aufladen des Kondensators. Der Ladestrom wird nach
Gesetzen des verzweigten Stromkreises zum Strom von 500 mA addiert.
2.1.2. Ersetzt man die Gleichspannung durch die Wechselspannung 18,0 V (Frequenz 50,0 Hz), so
beträgt die Gesamtstromstärke 545 mA.
Berechnen Sie die Kapazität C des Kondensators. Zeichnen Sie ein maßstäbliches Zeigerdiagramm und
geben Sie den Betrag der im Stromkreis auftretenden Phasenverschiebung zwischen Uges und I gesan.
Parallelschaltung von Wechselstromwiderständen:
2.1.3. Das ohmsche Bauelement R1 wird nun durch eine Spule ersetzt, um die Phasenverschiebung
zwischen der anliegenden Spannung und der Gesamtstromstärke aufzuheben. Berechnen Sie die
Induktivität dieser Spule. Der ohmsche Widerstand der Spule darf vernachlässigt werden.
Für 2.1.1 bis 2.1.3 erreichbare BE-Anzahl: 9
2.2. Ein Kondensator wird aufgeladen. Durch Betätigen eines Umschalters zum Zeitpunkt t=0 wird der
Kondensator über ein ohmsches Bauelement mit R = 52,2 kW entladen und die Stromstärke zu
verschiedenen Zeitpunkten gemessen. Zum Zeitpunkt t=0 beträgt die Spannung am Kondensator 180 V.
Es ergibt sich folgende Messreihe:
t in s
2,0
4,0
6,0
8,0
10
12
14
16
18
20
I in mA
2,2
1,4
0,86
0,54
0,34
0,22
0,14
0,086
0,054
0,034
2.2.1. Geben Sie die Stromstärke zum Zeitpunkt t = 0 an.
1. Möglichkeit:
2. Möglichkeit: Bestimmen des Schnittpunktes mit der y-Achse mit dem GTR
2.2.2. Ermitteln Sie die Gesamtladung des Kondensators und geben Sie dessen Kapazität an.
Eingabe der Wertepaare in den GTR, Regression nach e x.
Kurve zeichnen, Integration im bestimmten Zeitintervall:
Für 2.2.1 und 2.2.2 erreichbare
BE-Anzahl: 4
Lösungen zur Abiturprüfung 2001
Physik - Leistungskurs
Teil B
Aufgabe B: Thermodynamik / Wellenoptik
Carnot'scher Kreisprozess
1.
Skizzieren Sie das p-V-Diagramm des Carnot'schen Kreisprozesses und ordnen Sie die jeweiligen
Zustandsänderungen zu.
I - II Isotherme Expansion
II - III Adiabatische Expansion
III - IV Isotherme Kompression
IV - I Adiabatische Kompression
Erreichbare BE Anzahl: 3
2.
Der in der Abbildung dargestellte Kreisprozess wird von
Argongas im Uhrzeigersinn durchlaufen. Dabei gilt für Zustand
1: p 1 = 100 kPa, V1 = 125 l, und T 1 = 300K. Die
Zustandsänderung vom Zustand 2 nach Zustand 3 verläuft
isotherm.
2.1. Berechnen Sie die Masse des eingeschlossenen Gases.
2.2. Geben Sie die Temperatur im Zustand 2 an.
Für 2.1 und 2.2 erreichbare BE Anzahl:3
2.3. Bestimmen Sie für die einzelnen Zustandsänderungen jeweils die übertragene Wärme, die
Volumenarbeit und die Änderung der inneren Energie.
Prozess 1 - 2:
Prozess 2 - 3:
Prozess 3 - 1:
Erreichbare BE Anzahl: 6
2.4. Ermitteln Sie den thermodynamischen Wirkungsgrad dieses Kreisprozesses.
Erreichbare BE-Anzahl: 2
3.
Eine schwach gekrümmte plankonvexe optische Linse liegt auf einer planparallelen Glasplatte.
Auf die Anordnung fällt paralleles, einfarbiges Licht. Im reflektierten Licht beobachtet man unter
gewissen Bedingungen helle und dunkle Ringe. Erklären Sie deren Entstehung.
Reflexion der Lichtwellen erfolgt zum Teil an der unteren
Linsenkrümmung und bei senkrechtem Einfall auch an der Oberseite
der Glasplatte.
Durch unterschiedliche opt. Weglängen und durch Phasensprung
um p/2 an der Glasplatte entsteht ein Gangunterschied zwischen den
Teilwellen des monochromatischen Lichtes.
Diese Interferenz führt zu kreisförmigen Gebieten mit
maximaler Verstärkung und solcher mit Auslöschung, die als
helle und dunkle Ringe (NEWTONsche Ringe) sichtbar werden.
Erreichbare BE Anzahl: 3
.
4.
Optische Aktivität von Stoffen
Beschreiben Sie ein Experiment, mit dem entschieden werden kann, ob eine Lösung optisch aktiv ist !
Benötigt werden:
(Monochromatische) Lichtquelle,
2 Polarisationsfilter (1 Polarisator
und 1 Analysator), Küvette für
die zu untersuchende Lösung.
Verfahrensweise: Zunächst
werden ohne eingesetzte Küvette
Polarisator und Analysator
senkrecht zueinander eingestellt,
so dass das polarisierte Licht bei
direkter Beobachtung möglichst
vollständig ausgelöscht wird.
Anschließend wird zwischen die
beiden Filter die zu
untersuchende Lösung gebracht. Erfolgt jetzt eine Aufhellung, so wurde die Schwingungsebene des
polarisierten Lichtes gedreht, die Lösung ist optisch aktiv. Je nachdem, in welche Richtung der Analysator
nachzudrehen ist, um wieder vollständige Dunkelheit zu erreichen, kann in rechts- oder linksdrehende,
optisch aktive Lösungen unterschieden werden.
Erreichbare BE Anzahl: 3
Lösungen zur Abiturprüfung 2001
Physik - Leistungskurs
Teil C
Aufgabe C:
Wählen Sie eine der nachstehenden Aufgaben aus und bearbeiten Sie diese.
Aufgabe C 1: Elektrizitätslehre
Führen Sie Messungen und Berechnungen an einer SI -Diode durch. Planen Sie das Experiment gemäß den
folgenden Aufgabenstellungen und fordern Sie beim Aufsicht führenden Lehrer die erforderlichen Geräte und
Hilfsmittel an.
1.
Untersuchen Sie experimentell die Abhängigkeit der Stromstärke in Durchlassrichtung von der über der
Diode anliegenden Spannung U D. Verwenden Sie dabei den Ihnen übergebenen Vorwiderstand
(Schutzwiderstand). Fertigen Sie eine zugehörige Schaltskizze an.
Schaltskizze:
Beachten:
Spannungsrichtige Schaltung (in der Aufgabenstellung: über die Diode),
Messung im kleinen Spannungsbereich, damit Schwellenwert der Spannung erkennbar wird.
Erreichbare BE Anzahl: 5
2.
Berechnen Sie jeweils den Widerstand R D der Diode und zeichnen Sie das zugehörige RD - UD Diagramm.
Erreichbare BE Anzahl: 3
3.
Führen Sie eine Fehlerbetrachtung durch (Beurteilen der Genauigkeit der Messwerte sowie der
Ergebnisse)
Erreichbare BE Anzahl: 1
4.
(Diese Teilaufgabe ist nicht experimentell zu bearbeiten.)
Ein ohmsches Bauelement mit dem Widerstand R = 1,0 kΩ wird parallel zur von Ihnen in Aufgabe 1
verwendeten Diode geschaltet. An zwei Stellen im Stromkreis wird die Stromstärke gemessen (siehe
Abb.). Beide Messgeräte zeigen annähernd gleiche Messwerte.
Entscheiden Sie:
ob die Diode in Durchlass - oder in Sperrrichtung geschaltet wurde,
ob die anliegende Spannung 0,2 V oder 0,8 V beträgt.
Begründen Sie jeweils.
Bei annähernd gleichen Messwerten der beiden Messgeräte muss R D << R sein, Diode ist damit in
Durchlassrichtung gepolt. Die Diode hat die Schwellenspannung überschritten, also beträgt die
anliegende Spannung mindestens 0,5 V, hier also 0,8 V
Erreichbare BE Anzahl: 4
5.
Erläutern Sie die Sperrwirkung einer Halbleiterdiode.
Kombination eines p- und eines n-dotierten Gebietes, zwischen beiden entsteht eine schmale,
ladungsträgerarme Grenzschicht, Sperrwirkung tritt ein, wenn am n -Gebiet „+“-Pol und am p-Gebiet „-“Pol anliegt, Elektronen aus dem n-Gebiet werden „abgesaugt“, Defektelektronen werden mit Elektronen
besetzt, Grenzschicht verbreitert sich damit und verhindert einen größeren Stromfluss als den der
Rekombination
Erreichbare BE Anzahl: 2