Mathematik hat Geschichte Teil 4 Griechen
Werbung

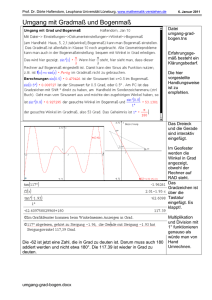
31.10.2011 Zahlen bei den Griechen 500-100vChr. Mathematik hat Geschichte Pythagoras y g Teil 4 Griechische Zahlschreibweise Euklid Griechen Archimedes Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 1 Zahlen bei den Griechen 500-100vChr. Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt3 Pythagoras - 580-500vChr. Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt2 Zahlen bei den Griechen 500-100vChr. Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt4 Pythagoras - 580-500vChr. Pythagoras von Samos, Philosoph, geb. um 580 v.Chr. Samos, gest. um 500 v.Chr. Metapontum (Unteritalien). Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt5 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt6 1 31.10.2011 Pythagoras - 580-500vChr. Euklid von Alexandria - 300vChr. Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt7 Euklid in Arabien Euklid in der alten Welt Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt9 Euklids Beweis des Kathetensatzes Interaktiv in GeoGebra Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt8 10 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. Web 11 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 12 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 2 31.10.2011 Euklid von Alexandria - 300vChr. Definitionen: 1. Was keine Teile hat, ist ein Punkt. 2. Eine Länge ohne Breite ist eine Linie. 3. Die Enden einer Linie sind Punkte. 4. Eine Linie ist gerade, wenn sie gegen die in befindlichen f Punkte auff einerlei Art gelegen g g 5. Was nur Länge und Breite hat, ist eine Fläche. Text aus Lexikon der Mathematik Spektrum 13 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. Postulate: 1. Es soll gefordert werden, daß sich von jedem Punkte nach jedem Punkte eine gerade Linie ziehen lasse. 2. Ferner, daß sich eine begrenzte gerade Linie stetig in g gerader Linie verlängern g lasse. 3. Ferner, daß sich mit jedem Mittelpunkt und Halbmesser ein Kreis beschreiben lasse. 4. Ferner, daß alle rechten Winkel einander gleich seien. Text aus Web Lexikon der Mathematik Spektrum 15 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. 5. (Parallelenpostulat) Endlich, wenn eine gerade Linie zwei gerade Linien trifft und mit ihnen auf derselben Seite innere Winkel bildet, die zusammen kleiner sind als zwei Rechte, so sollen die beiden geraden Linien, ins Unendliche verlängert, schließlich ß auff der Seite zusammentreffen, ff auf der die Winkel liegen, die zusammen kleiner sind als zwei Rechte. Text aus Lexikon der Mathematik Spektrum 17 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. Axiome: 1. Dinge, die demselben Dinge gleich sind, sind einander gleich. 2. Fügt man zu Gleichem Gleiches hinzu, so sind die Summen gleich. 3. Nimmt man von Gleichem Gleiches hinweg, g sind die Reste gleich. 4. Was zur Deckung miteinander gebracht werden kann, ist einander gleich. 5. Das Ganze ist größer als sein Teil. Text aus Lexikon der Mathematik Spektrum 14 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. 5. (Parallelenpostulat) Endlich, wenn eine gerade Linie zwei gerade Linien trifft und mit ihnen auf derselben Seite innere Winkel bildet, die zusammen kleiner sind als zwei Rechte, so sollen die beiden geraden Linien, ins Unendliche verlängert, schließlich ß auff der Seite zusammentreffen, ff auf der die Winkel liegen, die zusammen kleiner sind als zwei Rechte. Text aus Lexikon der Mathematik Spektrum 16 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Euklid von Alexandria - 300vChr. Diese Definitionen, Axiome und Postulate halten heutigen Anforderungen an logische Korrektheit nicht mehr stand. Zum einen erweist sich die Trennung nach Axiomen und Postulaten als nicht sinnvoll. Die Axiome erhalten nämlich nur dann eine Relevanz für die Geometrie, wenn konkrete geometrische Begriffe eingesetzt werden. Dann handelt es sich aber wiederum um geometrische Aussagen, Text aus also im Sinne Euklids um Postulate. In neueren Lexikon der Mathematik Arbeiten wird daher nicht mehr zwischen Axiomen Spektrum und Postulaten unterschieden, sondern nur von Axiomen gesprochen, worunter alle unbewiesenen Grundaussagen verstanden werden. 18 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 3 31.10.2011 Euklid von Alexandria - 300vChr. Hippokrates 470-410 v.Chr. Vor allem jedoch genügen die von Euklid gegebenen „Erklärungen“ nicht den logischen Ansprüchen an Definitionen. Vielmehr ist es unmöglich, alle auftretenden Objekte und Relationen zu definieren, da Definitionen nur auf Grundlage bereits bekannter Begriffe g möglich g sind. Einige g grundlegende g g Begriffe g (wie z. B. Punkt, Gerade usw.) müssen also als undefinierte Grundbegriffe an den Anfang gestellt werden. Ein logisch völlig korrekter axiomatischen Aufbau der Geometrie wurde von David Hilbert Text aus gegen Ende des 19. Jahrhunderts vorgestellt Lexikon der Mathematik (®Axiome der Geometrie). Spektrum 19 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Archimedes von Syrakus - 287-212 vChr. Hippokrates führte viele neue Arbeitsmethoden sein, so z. B. das Zurückführen von Web Problemen auf einfachere, bekannte. 20 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Archimedes von Syrakus 287-212 v.Chr. Die überragende wissenschaftliche Bedeutung des Archimedes ist durch die gesamte Wissenschaftsgeschichte seit der Antike niemals bestritten, oft sogar ins Phantastische überhöht worden und noch heute in Anekdoten lebendig. Bereits im 5./6. Jh. wurden die ersten Ausgaben der Werke des Archimedes editiert. Die heutigen Textkenntnisse gehen verweisend auf Werkausgaben des 9./10. Jh. und auf lateinische und arabische Übersetzungen des Mittelalters Text aus zurück. Einen Höhepunkt erlebte die Archimedes-Rezeption im 15./16. Jh. . Lexikon der Werke des Archimedes wurden jetzt ins Deutsche, Englische und Mathematik Spektrum Französische übersetzt. Sein Einfluss auf Kepler, Galilei und Torricelli ist unverkennbar. 21 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Archimedes Quadratur der Parabel Interaktiv in Euklid-Dynageo Web 22 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Archimedes Quadratur der Parabel Weiterer Beweis Hier macht Archimedes Den entscheidenden Schritt: Er beginnt die Reste bis zur Parabel mit weiteren solchen Dreiecken auszuschöpfen. Web GeoGebra archimedes-kasten.ggb Parabeln im Bärenkasten 23 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt GeoGebra archi4.ggb Web 26 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 4 31.10.2011 Archimedes Quadratur der Parabel Archimedes Quadratur der Parabel Zwei lila Dreiecke haben Fläche dieses Parallelogramm-Kastens. Darum nimmt nun nach Archimedes die Parabel zwei Drittel dieses Kastens ein. Bleiben zwei flächengleiche Reste. D gilt Das il für fü jede j d Parabelsehne und die zugehörige Tangente. Nun übernehmen die hellblauen Dreiecke die Rolle, die bisher das lila Dreieck gespielt hat. Zwei grüne Dreiecke haben also ¼ der Fläche von „ihrem“ hellblauen. Heute zeigt man das leicht mit Web Integralrechnung. GeoGebra archi4.ggb Web 27 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Die großen unlösbaren Probleme der Antike Scherungs-Beweise 28 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Die großen unlösbaren Probleme der Antike cos(3 ) cos( 2 ) cos( )cos(2 ) sin( )sin(2 ) • Das Delische Problem •Die Verdoppelung des Würfels cos( )(cos 2 ( ) sin 2 ( )) sin( )2sin( )cos( ) •Die Drittelung des Würfels k ( k 2 ((1 k 2 )) 2(1 ( k 2 )k •Die Di D Dreiteilung i il des d Winkels Wi k l Web k 3 k k 3 2k 2 k 3 4k 3 3 k •Die Quadratur des Kreises cos(3 ) a , cos( ) k 4k 3 3k a 0 Web 29 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Die Probleme führen auf Gleichungen 3. Grades, oder andere, Die nicht mit Zirkel und Lineal lösbar sind. 30 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Unlösbar mit Zirkel und Lineal Unlösbar mit Zirkel und Lineal die Winkeldrittelung die Winkeldrittelung Interaktiv in GeoGebra Web 31 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Interaktiv in GeoGebra Web Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 32 5 31.10.2011 Unlösbar mit Zirkel und Lineal Unlösbar mit Zirkel und Lineal: die Winkeldrittelung die Verdoppelung des Würfels Näherung mit Dies kann mit einem Blatt Papier falten. Konchoide Interaktiv in Euklid-Dynageo Auch DD‘ drittelt den Winkel Interaktiv in GeoGebra Web Web 33 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 34 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Unlösbar mit Zirkel und Lineal: Unlösbar mit Zirkel und Lineal: die Quadratur des Kreises die Quadratur des Kreises Web 35 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 36 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt Unlösbar mit Zirkel und Lineal: die Quadratur des Kreises 37 Prof. Dr. Dörte Haftendorn Universität Lüneburg www.uni-lueneburg.de/mathe-lehramt 6