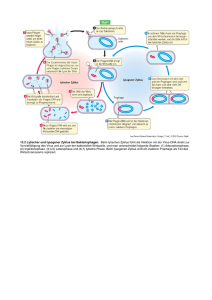
CNO-Zyklus - ITA Heidelberg

WS 2011/12
Institut für Theoretische Astrophysik, Heidelberg
H.-P. Gail
im Kosmos
Entstehung der chemischen Elemente
Seite: 5.1
Dieser Prozess wurde in seiner einfachsten Form, dem CN-Zyklus, zuerst
1938 von C.F. von Weizsäcker und 1939 von H. A. Bethe vorgeschlagen und Bethe gelang es auch, die Energieproduktionsrate zu berechnen. Der CN-Zyklus ist ein katalytischer Prozeß, der mit dem Einfang
eines Protons durch 12C beginnt und im Verlaufe dessen vier Protonen in einen 4He-Kern umgewandelt werden, wobei der 12C-Kern zum
Schluß wieder zurückgewonnen wird. Bei ausreichend hohen Temperaturen können trotz der hohen, abstoßenden Coulombpotentialschwelle –
allerdings nur mit einer geringen Wahrscheinlichkeit – die Protonen bei
Stößen mit Kernen der leichten Elemente die Potentialschwelle durchtunneln und unter Emission eines γ-Quants eingefangen werden. Der
hierauf beruhende Brennprozeß erfordert deswegen wesentlich höhere
Temperaturen als das Wasserstoffbrennen in der p-p-Kette, ist aber für
viele Sterne der dominierende Brennprozeß.
5. Wasserstoffbrennen im CNO-Zyklus
Seite: 5.2
endotherm. Sie könnte nur bei extrem hohen Temperaturen auftreten. Solche Reaktionen brauchen also nicht beachtet zu werden.
• Eine Austauschstreuung (p, n) ist nicht möglich, weil stets stark
möglich. Er wird aber mit zunehmender Ladung der Kerne immer schwieriger, weil die zu durchtunnelnde Coulombbarriere immer
höher wird. Die meisten der bei diesem Prozeß entstehenden Kerne
sind β + instabil mit kurzer Lebensdauer; das Zerfallsprodukt ist in
allen Fällen ein stabiler Kern.
• Der Einfang von Protonen ist stets exotherm, also energetisch
In Tabelle 5.1 sind für die stabilen Kerne von 12C bis 36Ar die Reaktionsenergien einiger Reaktionen angegeben, die durch Stöße mit Protonen
und α-Teilchen, also den häufigsten Kernen in der kosmischen Elementmischung, ausgelöst werden. Es ist folgendes festzustellen:
Ermöglicht werden dieser und weitere zyklische Prozesse durch die Tatsache, daß in einigen Fällen auf den Einfang eines Protons der hoch
angeregte Zwischenkern ein α-Teilchen emittiert.
5.1 Zyklische Brennprozesse
13
C
C
14
N
15
N
16
O
17
O
18
O
19
F
20
Ne
21
Ne
22
Ne
23
Na
24
Mg
25
Mg
26
Mg
26
Al
27
Al
28
Si
29
Si
30
Si
31
P
32
S
33
S
34
S
35
Cl
36
S
36
Ar
12
Ziel
τ1/2
1.943
597.9
7.549
7.291
122.2
12.125
0.598
64.5
5.597
6588
7.992
12.844
2.454
22.48
6.743 8.22×107
8.790
11.693
2.287
7.17
6.301 2.29×1013
8.272
7.471
4.14
11.581
2.735
4.14
5.585
150
7.286
8.863
2.285
2.51
5.218
1.528
6.367
8.506
8.402
1.890
1.23
(p,γ)
-7.557
-4.064
-2.922
4.964
-5.218
1.193
3.980
8.114
-4.132
-1.750
-1.675
2.379
-6.859
-3.142
-1.826
-1.871
1.594
-7.700
-4.832
-2.378
1.917
-4.211
-1.526
-0.631
1.865
0.544
-4.355
(p,α)
-18.390
-3.004
-5.931
-3.543
—
-3.544
-2.450
-4.031
-16.100
-4.305
-3.624
-4.842
-14.800
-5.044
-4.797
—
-5.598
-14.580
-5.743
-5.030
-6.218
-13.780
-6.358
-6.203
-6.763
-1.920
—
(p,n)
7.161
6.357
4.404
4.012
4.730
7.347
9.667
10.465
9.314
9.885
10.616
10.098
9.986
11.133
10.650
10.417
9.664
6.946
7.111
7.917
6.998
6.641
6.792
7.213
7.213
6.809
7.044
(α, γ)
-8.507
2.214
-4.737
-6.430
-12.145
0.588
-0.700
-1.949
-7.221
2.555
-0.482
-2.971
-7.193
2.655
0.036
-0.910
-2.652
-8.135
-1.532
-3.504
-5.572
-8.628
-2.002
-4.629
-5.866
-3.066
-8.685
(α,n)
Zyklische Brennprozesse
Seite: 5.3
Tabelle 5.1:
Energien (in
MeV) der Reaktionen leichter
Kerne mit p und α-Teilchen.
Bei der (p,γ) Reaktion sind
die β + Zerfallszeiten (in sec)
der Produktkerne angegeben,
sofern diese instabil sind.
Seite: 5.4
möglich, weil stark endotherm. Es es gibt aber einige exotherme
(α, n) Reaktionen, die Neutronen freisetzen, die ihrerseits wieder mit
anderen Kernen reagieren können. Dieser Prozeß ist außerordentlich
wichtig für den Aufbau schwerer Kerne, erfordert wegen der hohen
zu überwindenden Coulombbarriere aber sehr hohe Temperaturen.
• Eine Austauschstreuung (α, n) ist in den meisten Fällen nicht
möglich. Die hohe Coulombbarriere, die dabei überwunden werden
muß, macht diesen Prozeß im Vergleich zum Protoneneinfang sehr
unwahrscheinlich.
• Der Einfang von 4He Kernen ist stets exotherm, also energetisch
können deswegen selbst bei sehr hohen Temperaturen nicht auftreten. Es gibt aber einige exotherme (p, α) Reaktionen, bei denen nach
einer Serie von Protoneneinfängen eine (p, α) Reaktion zum Ausgang zurück führen kann. Darauf beruhen die nachfolgend behandelten Brennprozesse, die auch für die Nukleosynthese im Kosmos sehr
wichtig sind.
• Die meisten (p, α) Reaktionen sind ebenfalls stark endotherm und
Zyklische Brennprozesse
Seite: 5.5
3. Ein Zyklus, der beim 20Ne beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 23Na endet, wenn eine (p, α) Reaktion zum
20
Ne zurückführt. Alternativ kann an dieser Stelle statt der (p, α)
Reaktion auch eine (p, γ) Reaktion weiter zum 24Mg führen.
2. Ein Zyklus, der beim 16O beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 19F endet, wenn eine (p, α) Reaktion zum
16
O zurückführt. Alternativ kann an dieser Stelle statt der (p, α) Reaktion auch eine (p, γ) Reaktion weiter zum 20Ne führen. Innerhalb
dieses Zyklus können (p, α) Reaktionen beim 17O und 18O auch in
den ersten Zyklus zurückspringen.
1. Ein Zyklus, der beim 12C beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 15N endet, wenn eine (p, α) Reaktion zum
12
C zurückführt. Alternativ kann an dieser Stelle natürlich statt der
(p, α) Reaktion auch eine (p, γ) Reaktion weiter zum 16O führen.
Hier werden die Prozesse betrachtet, die bei den niedrigsten Temperaturen ablaufen können. Das sind die Reaktionen von Protonen mit
den leichtesten Kernen, da für solche Reaktionen die zu überwindenden
Coulombbarrieren am niedrigsten sind. Eine Inspektion der Tabelle 5.1
zeigt, daß im Prinzip folgende zyklische Prozesse möglich sind:
Zyklische Brennprozesse
Seite: 5.6
Wegen der zunehmend höheren Kernladungszahl der beteiligten Kerne
für die jeweiligen Zyklen werden die zu überwindenden Coulombbarrieren bei den verschiedenen Zyklen immer höher, sodaß höhere Zyklen
jeweils auch erst bei höheren Temperaturen auftreten. Nur die ersten
vier scheinen tatsächlich unter bestimmten Bedingungen im Inneren von
Sternen abzulaufen.
6. Ein Zyklus, der beim 32S beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 35Cl endet, wenn eine (p, α) Reaktion zum 32S
zurückführt. Alternativ kann an dieser Stelle statt der (p, α) Reaktion auch eine (p, γ) Reaktion weiter zum 36Ar führen.
5. Ein Zyklus, der beim 28Si beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 31P endet, wenn eine (p, α) Reaktion zum 28Si
zurückführt. Alternativ kann an dieser Stelle statt der (p, α) Reaktion auch eine (p, γ) Reaktion weiter zum 32S führen.
4. Ein Zyklus, der beim 24Mg beginnt, drei Protoneneinfänge nacheinander umfaßt, und beim 27Al endet, wenn eine (p, α) Reaktion zum
24
Mg zurückführt. Alternativ kann an dieser Stelle statt der (p, α)
Reaktion auch eine (p, γ) Reaktion weiter zum 28Si führen.
Zyklische Brennprozesse
Abbildung 5.1: Die zyklischen Prozesse niedrigster Ordnung
Zyklische Brennprozesse
Seite: 5.7
Abbildung 5.2: Die zyklischen Prozesse höherer Ordnung
Zyklische Brennprozesse
Seite: 5.8
+
+
+
+
+
γ
e+ + ν
γ
γ
e+ + ν
Zeit
≈ 6 103 a
9.7 m
≈ 2 103 a
≈ 8 105 a
122.2 s
Q
1.934
1.190
7.549
7.291
1.732
Seite: 5.9
Die Protoneneinfangzeiten gelten für eine Temperatur von 2 × 107 K.
Die freigesetzten Energien sind in MeV angegeben. Bei den β + Zerfällen
sind dies die Maximalenergien der Teilchen.
C+p
13
N
13
C+p
14
N+p
15
O
12
Reaktion
−→ 13N
−→ 13C
−→ 14N
−→ 15O
−→ 15N
Die ersten Reaktionen im CN-Zyklus sind (siehe Abb. 5.1)
Im ersten der oben aufgeführten Zyklen sind die Ladungen der beteiligten Kerne am niedrigsten. Er läuft deswegen von allen diesen Zyklen bei
der niedrigsten Temperatur ab. Dieser Zyklus wird als der CN-Zyklus
bezeichnet.
5.2 Der CN-Zyklus
N+p
−→
12
C + 4He
≈ 3 101 a
Zeit
4.964
Q
Seite: 5.10
Im einzelnen besteht dieser Zyklus aus vier aufeinanderfolgenden pEinfängen, die wegen der Coulombabstoßung der Kerne nur in sehr
großen Zeitabständen aufeinanderfolgen.
15
Reaktion
Wenn der 15N-Kern mit einem Proton stößt und dieses die Coulombbarriere durchtunnelt, dann kann der hoch angeregte 16O-Compoundkern
sich entweder durch die Emission eines γ-Quants stabilisieren, oder er
kann exotherm in einen 4He und in einen 12C–Kern zerfallen. Dieser
Zerfall in 4He und 12C erfolgt bei niedrigen Temperaturen mit einer
wesentlich höheren Rate als der γ-Übergang. Die letzte Reaktion im
CN-Zyklus ist deswegen
CN-Zyklus
Seite: 5.11
Im folgenden wird der Normalfall behandelt, daß die Zerfallszeiten sehr
kurz gegenüber den Einfangzeiten sind.
Wegen der mit steigender Temperatur stark zunehmenden Wahrscheinlichkeit der Durchtunnelung der Coulombbarrieren können aber bei sehr
hohen Temperaturen die Protoneneinfangzeiten kürzer als die β + Zerfallszeiten werden. Bei normalen Brennprozessen in Sternen werden die
Temperaturen nie so hoch, daß dieser Fall auftritt, nur bei thermonuklearen Explosionen, speziell in Novae, muß dies beachtet werden.
Diesen Fall bezeichnet man als heißen CNO-Zyklus
Durch den Einfang eines Protons entstehen in zwei Fällen β +–instabile
Kerne, deren Zerfallszeiten kurz gegenüber der Einfangszeit für das
nächste Proton sind. Die instabilen Kerne sind deswegen bereits in einen
stabilen Kern zerfallen, ehe das nächste Proton eingefangen wird. In diesem Fall spricht man vom kalten CN-Zyklus (oder einfach CN-Zyklus).
CN-Zyklus
4
He + 2e+ + 2ν
(156)
Seite: 5.12
Die Reaktion 15N+p →12C+4He wird durch die Kernkräfte bestimmt,
während die Reaktionen 12C(p, γ)13N, 13C(p, γ)14N und 14N(p, γ)15O
durch elektromagnetische Kräfte bestimmt werden. Die Reaktion
15
N+p →12C+4He sollte deswegen schneller als die (p, γ)–Reaktionen
ablaufen, was auch tatsächlich der Fall ist. Die Reaktion 14N(p, γ)15O
hat die höchste Coulombbarriere unter den (p, γ)–Reaktionen und ist
die langsamste Reaktion im CN–Zyklus. Diese ist der ratenbestimmende
Reaktionsschritt des gesamten Prozesses.
mit einer Energiefreigabe von Q = 26.70 MeV. Diese Energie ist die
Summe der angegebenen Reaktionsenergien der (p, γ) und (p, α) Reaktionen, der Energien der β + Zerfälle und der Energie der Annihilation
der beiden Positronen mit Elektronen. Ein Teil dieser Energie ist in den
beiden Neutrinos enthalten, die den Stern ohne weitere Wechselwirkung verlassen. Die mittlere Energie der Neutrinos aus dem 13N Zerfall
ist 0.710 Mev und aus dem 15O Zerfall 1.00 MeV. Die effektive Energie, die pro vollständigem Umlauf im Zyklus freigesetzt wird, ist dann
Q = 24.99 MeV.
4p −→
Das Nettoergebnis des Kreisprozesses ist die Umwandlung
CN-Zyklus
Seite: 5.13
Obwohl die Häufigkeit von C klein ist, ist die Effektivität dieses Prozesses wegen der vielfachen Verwendung der C-Kerne sehr effektiv. Der
CN–Zyklus läuft bei hinreichend hoher Temperatur in jeder beliebigen
Elementmischung ab, die eine nicht verschwindende Menge der Kerne
12
C, 13C, 14N und 15N in der Ausgangsmischung enthält. Die Reaktionskette im CN-Zyklus erzeugt, wenn sich ein stationäres Gleichgewicht
innerhalb der Kette ausgebildet hat, eine bestimmte Mischung der genannten Kerne, die unabhängig von der Anfangszusammensetzung ist.
Der CN-Zyklus verändert allerdings nur die relative Häufigkeiten der
Kerne 12C, 13C, 14N und 15N relativ zueinander, aber nicht deren Gesamtmenge.
CN-Zyklus
Seite: 5.14
Sterne der ersten Sterngeneration enthalten nur die primordiale Elementmischung, die im Urknall synthetisiert wurde, also H, He und Spuren von Li, aber keine schwereren Kerne. Die schwereren Kerne werden
erst in fortgeschrittenen Entwicklungsstadien beim He–Brennen und
höheren Brennprozessen synthetisiert. Die gegenwärtigen Sterne sind
alle Sterne späterer Sterngenerationen, die die Produkte der Elementsynthese früherer Sterngenerationen enthalten. In diesen kann der CNZyklus bei genügend hoher Temperatur ablaufen. In den Sternen der
ersten Sterngeneration kann der CN-Zyklus dagegen noch nicht ablaufen. Sie brennen den Wasserstoff ausschließlich in den p-p-Ketten.
CN-Zyklus
Seite: 5.15
Abbildung 5.3: Energieniveaus der Kerne im CN-Zyklus bis 10 MeV über dem Grundzustand, bei 16O bis 15 MeV über dem Grundzustand
CN-Zyklus
Seite: 5.16
Die Reaktionsquerschnitte aller Reaktionen im CN–Zyklus sind im Labor gemessen worden, um genaue Reaktionsraten bestimmen zu können.
Alle drei (p, γ)–Prozesse werden in ihrer Rate durch direkten Einfang
in den Grundzustand bestimmt. In Abb. 5.3 sind die relative Energie
der Grundzustände der Kerne bei den Reaktionen dargestellt und deren
tiefste Energieniveaus innerhalb etwa 10 MeV über dem Grundzustand.
In allen Fällen gibt es im Bereich oder in der Nähe der Reaktionsenergie
angeregte Niveaus im Produktkern, sodaß den Reaktionen in gewissem
Umfang resonanter Einfang in angeregte Niveaus überlagert sind.
5.3 Raten der Prozesse im CN-Zyklus
Abbildung 5.4: Termschema des
14
N(p,γ)15O auftritt.
15
Seite: 5.17
O Kerns, der als Zwischenzustand bei der Reaktion
Raten der Prozesse im CN-Zyklus
Abbildung 5.5: S-Faktor für die Reaktion
Grundzustand.
14
Seite: 5.18
N(p,γ)15O mit Rekombination in den
Raten der Prozesse im CN-Zyklus
Abbildung 5.6: S-Faktor für die Reaktion
6.79 MeV Zustand.
14
Seite: 5.19
N(p,γ)15O mit Rekombination in den
Raten der Prozesse im CN-Zyklus
Seite: 5.20
Bei niedrigen Brenntemperaturen (T ≤ 108 K) sind die β +-Zerfallszeiten
der instabilen Kerne kurz gegenüber den Zeitskalen für Protoneneinfang. Reaktionen der instabilen Kerne mit Protonen können unter diesen Umständen vernachlässigt werden (kalter CN-Zyklus). Für die am
CN–Zyklus beteiligten Kerne gelten dann folgende Reaktionsgleichungen:
Der langsamste der drei (p, γ)–Prozesse im CN–Zyklus ist die
14
N(p, γ)15O Reaktion. Das bedeutet, daß sich die prozessierten Kerne bei 14N stauen“, weil es von da aus nur sehr langsam weitergeht.
”
Nach einer gewissen Zeit sammelt sich dann fast alles ursprünglich vorhandene C-N-Material im 14N Kern an und die Häufigkeit der anderen
Kerne im CN–Zyklus wird durch das Reaktionsgleichgewicht mit 14N
bestimmt.
5.4 Isotopengleichgewicht innerhalb des CN–Zyklus
dt
d n15N
dt
d n15O
dt
d n14N
dt
d n13C
dt
d n13N
dt
d n12C
= +
= +
= +
= +
= +
= −
τ5
1
τ4
1
τ3
1
τ2
1
τ1
1
τ1
1
τ3
n15O −
n14N −
τ6
1
τ5
1
np n13C −
n13N −
1
np n12C −
np n12C +
n13N
np n15N
np n14N
np n15N
np n15O
τ4
1
np n13C
τ2
1
τ6
1
np n18O
np n17O
τ8
1
τ7
im CNO–Zyklus: +
im CNO-Zyklus: +
1
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.21
τ1
τ6
τ1
n12C .
n12C
Seite: 5.22
Diese Isotopenverhältnisse sind abhängig von der Brenntemperatur, da
τ1, τ3 und τ6 stark von der Temperatur abhängen.
Es stellt sich also im stationären Gleichgewicht im CN–Zyklus ein ganz
bestimmtes Verhältnis für die Isotopenhäufigkeiten ein:
n12C
τ1
n14C
τ1
=
,
=
.
(157)
n13C
τ3
n15N
τ6
n15N =
n14N =
τ4
Im Gleichgewicht sind die linken Seiten dieser Gleichungen gleich null
und es folgt für die einzelnen Teilchendichten
τ3
n13C =
n12C
τ1
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.23
Abbildung 5.7: Häufigkeit der einzelnen Isotope von C, N, und O relativ zur Gesamtzahl dieser Nuklide in Abhängigkeit von der Brenntemperatur im stationären
Gleichgewicht im CN–Zyklus und im CNO–Zyklus.
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.24
Tabelle 5.2: Isotopenhäufigkeitsverhältnisse von Kohlenstoff und Stickstoff
n12C/n13C
n14N/n15N
Planetensystem
89
272
CN–Zyklus
3. . . 4
≈ 20 000 . . . 40 000
Abbildung 5.7 zeigt die Häufigkeiten der Isotope von C und N im stationären Gleichgewicht im CN–Zyklus in Abhängigkeit von der Brenntemperatur. Die Häufigkeit von C ist im Gleichgewicht sehr viel kleiner
als die Häufigkeit von N. Die kosmische Häufigkeit von C ist dagegen
sehr viel größer als die von N. Wenn beim Wasserstoffbrennen nach dem
CN-Zyklus das Gleichgewicht erreicht wird, dann wird praktisch der
ganze urspünglich vorhandene Kohlenstoff in 14N umgewandelt. Dieser
Prozeß ist die wichtigste Quelle für N im Kosmos.
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.25
Abbildung 5.8: Verhältnisse der Isotopenhäufigkeiten im stationären Gleichgewicht
im CNO–Zyklus.
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.26
Das Isotopenverhältnis für die Kohlenstoffisotope im Planetensystem
weicht stark vom Gleichgewichtsverhältnis im CN–Zyklus ab. Der größte
Teil des Kohlenstoffs im Kosmos wird in einem anderen Prozeß erzeugt,
in dem das 12C dominiert (im He-Brennen).
Die Häufigkeitsverhältnisse n12C/n13C und n14N/n15N sind in Abb. 5.8
dargestellt. Sie hängen beide etwas, aber nicht sehr stark von der Brenntemperatur ab. Tabelle 5.2 gibt den Wertebereich der n12C/n13C und
n14N/n15N Isotopenverhältnisse im CN–Zyklus und zum Vergleich die
entsprechenden Werte im Sonnensystem an. Das Isotopenverhältnis für
Stickstoff im Sonnensystem ist deutlich kleiner als der Bereich der Werte, die sich im CN–Zyklus einstellen, ist aber sehr hoch. Das deutet
darauf hin, daß der Stickstoff im Kosmos weitgehend durch Einstellung
des Isotopengleichgewichts im CN-Zyklus erzeugt wird, daß aber noch
ein anderer Prozeß existiert, in dem 15N in erheblich größerem Anteil
erzeugt wird als im CN-Zyklus.
Isotopengleichgewicht innerhalb des CN–Zyklus
Seite: 5.27
Dieser Prozeß füttert den Sauerstoff in den CN–Zyklus hinein. Allerdings sind die hierfür erforderlichen Temperaturen sehr hoch und deswegen sind die Zeitskalen bei den Temperaturen des Wasserstoffbrennens auf der Hauptreihe hierfür so groß, daß der Sauerstoff während der
Lebensdauer auf der Hauptreihe durch diesen Prozeß nicht vollständig
verbraucht wird.
Der in den Sternen vorhandene Sauerstoff kann ebenfalls eine Kette von
Kernreaktionen durchlaufen
16
O + p −→ 17F + γ
1010 a
17
F −→ 17O + e+ + ν
64.5 s
17
O + p −→ 14N + 4He
≈ 108 a
5.5 Der CNO-Bizyklus
Seite: 5.28
Abbildung 5.9: Verlauf des S(E) Faktors mit der Energie für die Reaktion 15N(p, γ)16O
im CNO–Bizyklus. Blaue Kreise: Hebbard (1960). Grüne Dreiecke: Rolfs & Rodney
(1974). Rote Quadrate: Bemmerer (2009). Gestrichelte Linie: Theoretischer Fit, Mukhamedzhanov et al. (2008).
Der CNO-Bizyklus
N (p, γ) 16O (p, γ) 17F (e+ν) 17O (p, α) 14N
Seite: 5.29
hineingefüttert. Im Endeffekt wird der ursprünglich vorhandene Sauerstoff beim Brennen im CNO–Zyklus allmählich zerstört, wenn sich ein
Gleichgewichtszustand einstellen kann.
15
Da diese Reaktion durch die elektromagnetische Wechselwirkung bestimmt wird, während die konkurrierende Reaktion 15N(p, α)12C durch
die Kernkräfte bestimmt wird, ist das Verzweigungsverhältnis der beiden Ausgangskanäle 12C+α bzw. 16O+γ von der Größenordnung 103 : 1.
Nur ein verschwindend kleiner Teil des Materials aus dem CN–Zyklus
wird in die Nebenkette
Es gibt im CN–Zyklus ferner eine Nebenreaktion, durch die 16O gebildet
wird
15
N + p −→ 16O + γ .
(158)
Der CNO-Bizyklus
Seite: 5.30
Abbildung 5.10: Zeitliche Entwicklung der Isotopenhäufigkeiten der Elemente C, N
und O im im CNO–Bizyklus, dargestellt als Funktion der Zahl der Protonen, die pro
ursprünglich vorhandenem C, N und O Kern eingefangen wurden.
Der CNO-Bizyklus
Seite: 5.31
Die Nebenkette ist für die Energieproduktion im Stern nicht besonders wichtig, sie bestimmt aber die Synthese von 18O und die Synthese
schwererer Elemente, da von 17O aus weitere Nebenketten abzweigen:
17
O + p −→ 18F + γ
18
F −→ 18O + e+ + ν
18
O + p −→ 15N + α
−→ 19F + γ
19
F + p −→ 16O + α
−→ 20Ne+ γ
Ausgehend von 20 Ne werden dann weitere schwere Elemente gebildet.
Das vollständige Reaktionsschema im CNO–Bizyklus zeigt Abb. 5.1.
Die zeitliche Entwicklung der Isotopenhäufigkeiten von C, N und O
im CNO–Bizyklus und den Übergang zum Gleichgewicht zeigt die
Abb. 5.10. Das Gleichgewicht wird erst nach relativ langer Zeit erreicht, da die Nebenkette im CNO–Bizyklus nur sehr langsam durchlaufen wird.
Der CNO-Bizyklus
Seite: 5.32
Abbildung 5.11: Energieerzeugungsraten beim Wasserstoffbrennen nach der p-p–
Kette und im CNO–Zyklus.
Der CNO-Bizyklus
Seite: 5.33
Wegen der, verglichen mit den Reaktionen in den p-p–Ketten, deutlich
höheren Coulombbarrieren der beteiligten Kerne, erfordert der CN–
Zyklus deutlich höhere Temperaturen, um effektiv ablaufen zu können.
Abbildung 5.11 zeigt die Energieerzeugungsrate beim Wasserstoffbrennen im CNO–Zyklus und nach der p-p–Kette. Bei niedrigen Temperaturen ist die Energieerzeugungsrate durch den CNO–Zyklus sehr niedrig; dort dominiert die Energieerzeugung in den p-p–Ketten. Bei hohen
Temperaturen ist aber die Energieerzeugung im CNO–Zyklus weitaus
effektiver. Bei Sternen mit bis zu etwas über einer Sonnenmasse sind
die Zentraltemperaturen relativ niedrig, sodaß dort die p-p–Kette dominiert. Bei Sternen mit höherer Masse sind die Zentrumstemperaturen
viel höher, und der CNO–Zyklus dominiert in diesen Sternen die Energieproduktion.
Der CNO-Bizyklus