Quadratische Funktionen

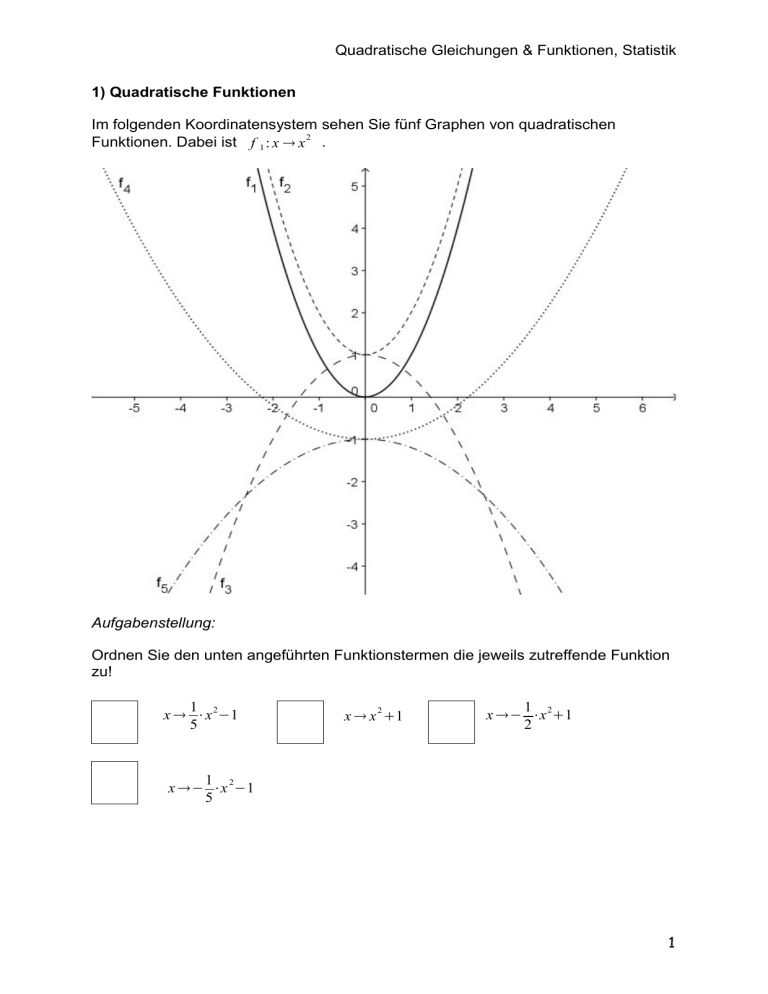
Quadratische Gleichungen & Funktionen, Statistik
1) Quadratische Funktionen
Im folgenden Koordinatensystem sehen Sie fünf Graphen von quadratischen
Funktionen. Dabei ist f 1 : x → x 2 .
Aufgabenstellung:
Ordnen Sie den unten angeführten Funktionstermen die jeweils zutreffende Funktion
zu!
1
x → ⋅x 2−1
5
2
x → x +1
1
x →− ⋅x 2+1
2
1
x →− ⋅x 2−1
5
1
Quadratische Gleichungen & Funktionen, Statistik
2) Nullstellen einer quadratischen Funktion
Gegeben sei eine quadratische Funktion mit f (x )=a⋅x 2+b , mit a≠0 ; a , b∈ℝ .
Aufgabenstellung:
Kreuzen Sie an, welche der folgenden Aussagen über die Nullstellen einer
quadratischen Funktion zutreffend bzw. nicht zutreffend sind:
zutreffend
nicht zutreffend
Gilt a > 0 und b < 0, dann hat die Funktion
genau zwei verschiedene reelle Nullstellen.
Gilt a < 0 und b < 0, dann hat die Funktion
genau zwei verschiedene reelle Nullstellen.
Gilt a > 0 und b > 0, dann hat die Funktion
genau zwei verschiedene reelle Nullstellen.
Gilt a < 0 und b > 0, dann hat die Funktion
genau zwei verschiedene reelle Nullstellen.
Gilt b = 0, dann hat die Funktion genau eine
reelle Nullstelle.
3) Lineare und quadratische Funktion
In der nachfolgenden Grafik ist der Graph der Funktion f mit f(x) = x 2 und der Graph
einer linearen Funktion g dargestellt.
Aufgabenstellungen:
a) Ermitteln Sie eine Gleichung der linearen Funktion g!
b) Der Graph der Funktion f und der Graph der Funktion g schneiden einander.
Berechnen Sie die Koordinaten der Schnittpunkte!
2
Quadratische Gleichungen & Funktionen, Statistik
4) Aussagen zur quadratischen Gleichung
Gegeben sind quadratische Gleichungen der Form
a≠0 ; a , b , c ∈ℝ .
a⋅x 2 +b⋅x+c=0 , mit
Kreuzen Sie an, welche der folgenden Aussagen über die Lösungen von
quadratischen Gleichungen der oben angegebenen Form zutreffend bzw. nicht
zutreffend sind!
zutreffend
nicht zutreffend
Jede dieser quadratischen Gleichungen hat genau
zwei reelle Lösungen.
Jede dieser quadratischen Gleichungen hat maximal
zwei reelle Lösungen.
Jede dieser quadratischen Gleichungen hat
mindestens eine reelle Lösung.
Es gibt quadratische Gleichungen dieser Form, die
keine reelle Lösung besitzen.
5) Quadratische Gleichung
Gegeben sei die Gleichung x² - 4 · x + k = 0.
Für welche Werte von k hat die Gleichung zwei, eine bzw. keine reelle Lösung?
6) Quadratische Gleichung
Gegeben ist die quadratische Gleichung a · x² + b · x + c = 0 mit a , b , c ∈ℝ .
Beschreiben Sie die möglichen reellen Lösungsfälle in Abhängigkeit von den
Parametern a, b, c!
7) Quadratische Gleichung
Gegeben ist die quadratische Gleichung x² + k · x + 5 = 0 über
G=ℝ , k ∈ℝ .
Welchen Wert muss k annehmen, damit die quadratische Gleichung genau eine
Lösung hat?
8) Quadratische Gleichung
Für welche Werte von a ∈ℝ hat die Gleichung x² = a keine reelle Lösung,
genau eine reelle Lösung bzw. zwei reelle Lösungen?
3
Quadratische Gleichungen & Funktionen, Statistik
9) Lösungen einer quadratischen Gleichung
Gegeben sei die quadratische Gleichung u·x² + v·x + w = 0, mit u≠0 ;
u , v , w∈ℝ .
Kreuzen Sie an, welche der folgenden Aussagen über die Lösung(en) dieser
quadratischen Gleichung zutreffend bzw. nicht zutreffend sind:
zutreffend
nicht zutreffend
Eine quadratische Gleichung ux² + v·x + w = 0 hat
genau zwei reelle Lösungen, wenn gilt: v² – 4u·w > 0.
Eine quadratische Gleichung ux² + v·x + w = 0 hat
genau zwei reelle Lösungen, wenn gilt: v² – 4u·w < 0.
Eine quadratische Gleichung ux² + v·x + w = 0 hat
genau eine reelle Lösung, wenn gilt: v² – 4u·w = 0.
10) Lösungen einer quadratischen Gleichung
Gegeben sei die quadratische Gleichung 3x² + 4x + c = 0, mit
c ∈ℝ .
zutreffend
nicht zutreffend
Die gegebene quadratische Gleichung hat genau zwei
Lösungen in der Menge der reellen Zahlen, wenn gilt:
c > 4/3 .
Die gegebene quadratische Gleichung hat genau zwei
Lösungen in der Menge der reellen Zahlen, wenn gilt:
c < 4/3 .
Die gegebene quadratische Gleichung hat genau eine
reelle Lösung, wenn gilt: c = 4/3
4
Quadratische Gleichungen & Funktionen, Statistik
11) Grundwehrdienst
Beim Stellungstermin wurden unter anderem die Körpergrößen von 120 Rekruten
festgehalten. Diese sind hier zusammengefasst in Form eines Diagramms
dargestellt:
Setzen Sie in den folgenden Aussagen die richtigen Zahlen ein:
Aus dem Diagramm kann man entnehmen, dass
ca. 50% der Rekruten kleiner als ……… cm sind.
jeder Rekrut mindestens ……… cm groß ist.
von den 120 Rekruten ca. ……… Rekruten mindestens 181 cm groß sind.
von den 120 Rekruten ca. ……… Rekruten größer als 168 cm sind.
ca. ……… Rekruten zwischen 168 cm und 181 cm groß sind.
12) Jahreseinkommen von Arbeiterinnen und Arbeitern
Im Jahre 2007 betrug das arithmetische Mittel der Netto-Jahreseinkommen der
529.157 österreichischen Arbeiterinnen € 8.837.-, jenes der 987.442
österreichischen Arbeiter € 15.638,-.
Ermitteln Sie das arithmetische Mittel der Netto-Jahreseinkommen aller 1,516.599
österreichischen Arbeiter(innen)!
13) Test
Sieben Schüler absolvieren einen Test. Das arithmetische Mittel, über alle von den
Schülern erreichten Punktwerte, ist 11. Ein achter Schüler, welcher während der
ersten Testung krank war, schreibt den Test nach. Nimmt man den von ihm
erreichten Punktwert dazu, erhöht sich das arithmetische Mittel über alle acht
Punktwerte auf 12.
Geben Sie an, wie viele Punkte der neue Schüler im Test erreicht hat!
5