Übungen zur Physik I fuer Chemiker und Lehramt mit

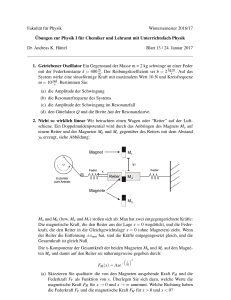
Fakultät für Physik
Wintersemester 2016/17
Übungen zur Physik I für Chemiker und Lehramt mit Unterrichtsfach Physik
Dr. Andreas K. Hüttel
Blatt 13 / 9. Februar 2017
1. Getriebener Oszillator Ein Gegenstand der Masse m = 2 kg schwinge an einer Feder
N
. Der Reibungskoeffizient sei b = 2 kgs m . Auf das
mit der Federkonstante k = 400 m
System wirke eine sinusförmige Kraft mit maximalem Wert 10 N und Kreisfrequenz
ω = 10 rad
s . Bestimmen Sie:
(a) die Amplitude der Schwingung
F0
A= q
= 0, 050 m
m2 (ω02 − ω 2 )2 + (bω)2
(b) die Resonanzfrequenz des Systems
r
ω0 =
rad
k
= 14, 14
→ ωres =
m
s
s
b
ω02 − √
2m
= 14, 14
rad
s
(c) die Amplitude der Schwingung im Resonanzfall
A=
F0
= 0, 354 m
bω0
(d) den Gütefaktor Q und die Breite ∆ω der Resonanzkurve.
√
km
Q=
= 14, 1
b
ω0
1
=1
∆ω =
Q
s
2. Nicht so wirklich linear Wir betrachten einen Wagen oder “Reiter” auf der Luftschiene. Ein Doppelmuldenpotential wird durch das Anbringen des Magnets Ma auf
einem Reiter und der Magneten Mb und Mc gegenüber des Reiters mit dem Abstand
y0 erzeugt, siehe Abbildung:
Ma und Mb (bzw. Ma und Mc ) stoßen sich ab. Man hat zwei entgegengerichtete Kräfte:
Die magnetische Kraft, die den Reiter aus der Lage x = 0 wegdrückt, und die Federkraft, die den Reiter in die Gleichgewichtslage x = 0 (ohne Magneten) zieht. Wenn
der Reiter die Entfernung ±xmin hat, sind die Kräfte entgegengesetzt gleich, und die
Gesamtkraft ist gleich Null.
Die x-Komponente der Gesamtkraft der beiden Magneten Mb und Mc auf den Magneten Ma und damit auf den Reiter sei näherungsweise gegeben durch:
2
− xx
FM (x) = Axe
0
(a) Skizzieren Sie qualitativ die von den Magneten ausgehende Kraft FM und die
Federkraft FF als Funktion von x. Überlegen Sie sich dazu, welche Werte die
magnetische Kraft FM für x → 0 und x → ∞ annimmt. Welche Richtung haben
die Federkraft FF und die magnetische Kraft FM für x > 0 und x < 0?
lim KM (x) = 0,
x→0
für
x>0:
lim KM (x) = 0
x→∞
FF (x) < 0, FM (x) > 0;
für
x<0:
FF (x) > 0, FM (x) < 0
(b) Berechnen Sie aus den Kräften FF (x) und FM (x) auf den Reiter die Beiträge
UF (x) und UM (x) der Feder und der Magnete zur potentiellen Energie und die
gesamte potentielle Energie U(x) als Funktion der Auslenkung x des Reiters.
Verwenden Sie die Anfangsbedingung U(0) = 0.
U(0) = 0
UM (x) = −
UF (x) = −
Zx
0
Zx
0
0
0
FM (x )dx = −
FF (x0 )dx0 = −
Zx
0
Zx
Ax e
1
−
dx = Ax02 e
2
0
x
x0
2
1
− Ax02
2
1
kx0 dx0 = kx2
2
0
2
x
1 2 − x
Ax0 e 0 −
1
U(x) = kx2 +
2
2
0 2
x
0 − x0
1 2
Ax
2 0
(c) Skizzieren Sie die potentiellen Energien UF (x), UM (x) und U(x) als Funktion
von x.
(d) Wo ist die Gleichgewichtslage des Reiters?
Nicht eindeutig definiert, in der linken oder der rechten Potentialmulde
gibt es ein stabiles Gleichgewicht und bei x = 0 ein instabiles Gleichgewicht.
3. Duffing Wir betrachten nun, wie der Reiter aus der vorherigen Aufgabe schwingt...
(a) Geben Sie die mit Hilfe des 2. Newtonschen Gesetzes die Differentialgleichung
für das in Aufgabe 2 skizzierte nichtlineare Pendel an, das durch einen geeigneten
Mechanismus von außen mit einer periodischen (sin) Kraft mit Amplitude F0 und
Kreisfrequenz ω getrieben wird.
2
− xx
mẍ + γ ẋ + kx − Axe
0
= F0 sin(ωt)
mit k = Federkonstante, F0 = Amplitude (Antrieb), γ = Reibungskoeffizient, ω = Kreisfrequenz des Antriebs
(b) Für kleine Auslenkungen x können Sie die Kraft FM bei x = 0 in eine TaylorReihe bis zur dritten Potenz in x entwickeln. Benutzen Sie diese Reihenentwicklung und finden Sie so eine Näherungsformel für FM .
2
− xx
FM (x) = Axe
0
→ Taylor:
d FM
x2 d2 FM
x3 d3 FM
x2
FM3 (x) = FM (0) + x
(0) +
(0) +
(0) = Ax 1 − 2
dx
2 d x2
6 d x3
x0
(c) Zeigen Sie mit dieser Näherungsformel, daß obige Differentialgleichung für geeignet kleine Auslenkung x in die Differentialgleichung eines Duffing-Oszillators
übergeht. Vergleichen Sie die Koeffizienten mit denen des Duffing-Oszillators
aus dem Vorlesungsskript (Gleichung 16.53) und bestimmen Sie so ω0 und β
aus Gleichung 16.53.
A 3
x = F0 sin(ωt)
x02
r
k−a
→ ω0 =
m
mẍ + bẋ + kx − Ax +
mω02 = k − A
β=
A
x02
4. Wiederrollung Über einer Rolle hängt ein masseloses, dünnes Seil, an dessen zwei
Enden Gewichte mit Massen m1 = 10 kg und m2 = 15 kg befestigt sind. Anfangs liegt
das leichtere Gewicht auf dem Boden, das schwerere Gewicht hängt in h = 3 m Höhe.
Das Seil kann auf der Rolle nicht rutschen, sondern hat ideale Haftreibung; die Rolle
beschreiben wir als homogene Kreisscheibe mit Radius 20 cm und Masse mr = 6 kg.
Zum Zeitpunkt t = 0 beginnt die schwerere Masse zu fallen und die leichtere Masse
anzusteigen. Berechnen Sie
(a) die Geschwindigkeit, mit der das 15kg-Gewicht auf dem Boden auftrifft
(b) die Winkelgeschwindigkeit der Rolle in diesem Moment
(c) die kinetische Energie beider Teilsysteme
Gratulation, dies war das letzte Übungsblatt (und es wird 31. Januar bis 3. Februar besprochen). In der letzten Vorlesungswoche (6. bis 10. Februar) finden die Übungsstunden statt,
aber als “Fragestunde” — also überlegen Sie sich schon mal, was Sie noch gerne wissen
möchten oder was nochmals erklärt werden sollte!