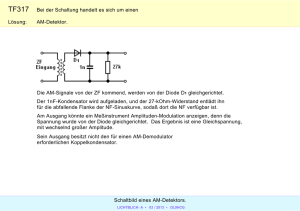
Hochkompaktes Umrichterleistungsteil mit sinusförmiger

Kompakter 690V-Umrichter mit SiCSchottkydioden für sinusförmige
Ausgangsspannung
Der Technischen Fakultät der
Universität Erlangen-Nürnberg
zur Erlangung des Grades
DOKTOR-INGENIEUR
vorgelegt von
Benno Weis
Erlangen, 2008
Als Dissertation genehmigt von
der Technischen Fakultät der
Universität Erlangen-Nürnberg
Tag der Einreichung:
10.10.2007
Tag der Promotion:
09.05.2008
Dekan:
Prof. Dr.-Ing. habil. J. Huber
Berichterstatter:
Prof. Dr-Ing. B. Piepenbreier
Prof. Dr. rer.nat. M. Stoisiek
2
Vorwort
Die vorliegende Arbeit entstand während meiner Tätigkeit als Entwicklungsingenieur im
Kompetenzzentrum Leistungselektronik des Bereiches Automation and Drives der Siemens
AG in Erlangen.
Bei Hrn. Prof. Dr.-Ing. B. Piepenbreier möchte ich mich für die freundliche Betreuung dieser
Arbeit, die konstruktiven Anregungen und die Übernahme des ersten Gutachtens bedanken.
Hrn. Prof. Dr. phil. nat. M. Stoisiek danke ich für die Übernahme des Koreferats, des zweiten
Gutachtens sowie die anregenden Diskussionen, die mein Verständnis für
Leistungshalbleiter erweitert haben.
Für die Anregung zu dieser Arbeit möchte ich mich ganz herzlich bei Hrn. Dr. rer.nat. H.
Mitlehner und Hrn. Prof. Dr.-Ing. M. Bruckmann bedanken. Des Weiteren bedanke ich mich
bei meinen Vorgesetzten, Hrn. G. Bock und Hrn. Dr.-Ing. E. Baudelot, für die wohlwollende
Unterstützung und das kreative, innovative Arbeitsumfeld. Bei meinen Kollegen, Hrn. Dr.-Ing.
H. Schierling, Hrn. Dr.-Ing. R. Polley, Hrn. Dr-Ing. F. Bauer, Hrn. Dipl.-Ing. R. Gospos und
Hrn. Dipl.-Ing. R. Freydman möchte ich mich für die anregenden Diskussionen sowie die
angenehme Arbeitsatmosphäre bedanken. Bei den Firmen infineon AG und SiCED GmbH,
insbesondere bei Hrn. Dr. M. Ruff und Hrn. Dr.-Ing. D. Peters, möchte ich mich für die
konstruktive Zusammenarbeit auf dem Gebiet der SiC-Schottkydioden bedanken.
Bei meinen Eltern möchte ich mich für die permanente Unterstützung bedanken, die sie mir
während meiner Schulzeit und meines Studiums zukommen ließen.
Der hohe private zeitliche Aufwand, der im Besonderen bei Dissertationen neben einer
Industrietätigkeit anfällt, hat für meine Familie eine besondere Belastung dargestellt. Deshalb
bedanke ich mich ganz besonders bei meiner Frau und meinen Kindern, die mir einen
großartigen Rückhalt geboten und während dieser Zeit viel Geduld entgegengebracht haben.
3
4
Inhaltsverzeichnis:
1
2
Einleitung ..........................................................................................................................7
Halbleiterbauelemente des motorseitigen Wechselrichters ............................................10
2.1
Der IGBT ................................................................................................................10
2.1.1 Trench-IGBT .......................................................................................................10
2.1.2 Planarer IGBT.....................................................................................................11
2.1.3 Ansteuerbedingungen beim Abschalten des IGBT.............................................13
2.1.3.1
Maximale Überspannung ............................................................................14
2.1.3.2
Abschaltfestigkeit im Kurzschlussfall ..........................................................14
2.1.3.3
Belastung der Komponenten der Potenzialtrennung ..................................17
2.1.3.4
Verlustersparnis durch schnelles Schalten .................................................20
2.1.4 Dynamische Sättigungsspannung ......................................................................21
2.2
Die Freilaufdiode ....................................................................................................24
2.2.1 Die Si-pn-Diode ..................................................................................................24
2.2.2 Die SiC-Schottkydiode........................................................................................29
2.2.2.1
Der Schottky-Kontakt ..................................................................................30
2.2.2.2
Die Driftzone ...............................................................................................34
2.2.2.3
Parallelschaltbarkeit von SiC-Schottkydioden ............................................35
2.2.2.4
Bestimmung der Chipgröße der SiC-Dioden ..............................................41
2.2.2.5
Dynamisches Abschaltverhalten der SiC-Schottkydiode ............................45
2.2.2.6
Einschaltverhalten der SiC-Schottkydiode..................................................49
2.3
Auslegung des Umrichters für verschiedene Dioden..............................................50
2.3.1 Berechnung der Verlustleistung im Umrichterbetrieb .........................................50
2.3.1.1
Berechnung der Durchlassverluste.............................................................50
2.3.1.2
Berechnung der Schaltverluste...................................................................53
2.3.1.3
Verluste bei Ausgangsfrequenz 0Hz...........................................................54
2.3.1.4
Verlustoptimierung für kleine Ausgangsfrequenzen ...................................57
2.3.2 Thermisches Modell............................................................................................60
2.3.3 Berechnung des erforderlichen Halbleiteraufwands ...........................................68
2.4
Unipolarer Hochvoltschalter ...................................................................................73
2.4.1 Struktur des SiC-JFET........................................................................................74
2.4.2 Durchlassverhalten .............................................................................................75
2.4.3 Nachbildung des Schaltverhaltens .....................................................................76
2.4.4 Berechnung des Halbleiterbedarfs im Umrichterbetrieb .....................................80
2.5
Moduldesign ...........................................................................................................85
3 Auslegung des Sinus-Ausgangsfilter ..............................................................................92
3.1
Bestimmung der auslegungsrelevanten Ausgangsspannung.................................92
3.2
Auslegung der Filterdrossel ....................................................................................97
3.2.1 Magnetische Dimensionierung der Filterdrossel.................................................98
3.2.1.1
Grundlagen .................................................................................................98
3.2.1.2
Bestimmung des Ripplestroms .................................................................100
3.2.2 Thermische Dimensionierung der Filterdrossel ................................................102
3.2.2.1
Kupferverluste...........................................................................................102
3.2.2.2
Hystereseverluste .....................................................................................102
3.2.2.3
Wirbelstromverluste ..................................................................................104
3.2.2.4
Integrations- und Kühlkonzept für den Sinusfilter .....................................105
3.2.3 Rückwirkung des Ripplestroms auf die Halbleiterdimensionierung ..................108
3.2.3.1
Simulation der zusätzlichen Halbleiterverluste .........................................108
3.2.3.2
Ermittlung des kostenoptimalen Ripplestromes........................................112
3.2.4 Auswahl der Schaltfrequenz .............................................................................114
3.3
Auslegung Kondensator .......................................................................................117
5
4
5
6
7
3.3.1 Dimensionierung der Filtereckfrequenz ............................................................117
3.3.2 Dämpfung des Filters........................................................................................120
3.3.2.1
Bestimmung der existierenden Dämpfung................................................120
3.3.2.2
Bestimmung der frequenzabhängigen Drosselverluste ............................121
3.3.2.3
Auswirkungen der Dämpfung und des Motors auf die
Übertragungscharakteristik........................................................................................122
3.3.3 Selbsterregung .................................................................................................124
3.4
Asymmetrischer Filter ...........................................................................................128
3.4.1 Spannungsbelastung des Motors .....................................................................129
3.4.2 Resonanz des asymmetrischen Filters.............................................................135
3.4.3 Lagerströme......................................................................................................137
3.5
EMV-Verhalten .....................................................................................................143
3.5.1 Grundlagen und Messaufbau ...........................................................................143
3.5.2 Leitungsgebundene Störaussendung ...............................................................145
3.5.3 Strahlungsgebundene Störaussendung ...........................................................149
Zusammenfassung........................................................................................................152
Abstract .........................................................................................................................154
Abkürzungen und Formelzeichen .................................................................................155
Literaturverzeichnis .......................................................................................................160
6
1 Einleitung
Stromrichter zur Regelung drehzahlveränderlicher Antriebe gewinnen in der Anwendung
immer mehr an Bedeutung. In zunehmendem Maße ersetzt diese Konfiguration die
klassische Lösung, bei der ein Motor direkt am Netz betrieben wird. Zum einen Teil ist dies
durch die vorteilhafte Performance der drehzahlveränderlichen Antriebe begründet, zum
anderen bieten drehzahlveränderbare Antriebe Möglichkeiten zur Energieeinsparung ([12],
[27]).
Netz
Gleichrichter
Wechselrichter
Zwischenkreis
Motorleitungen
und Motor
M
Abbildung 1: Standardmäßige Ausführung eines drehzahlveränderlichen Antriebes
Dem Motor wird hierbei durch den Frequenzumrichter ein in Frequenz und Amplitude
variables Spannungssystem geliefert, das durch Schalthandlungen des Wechselrichters aus
der konstanten Zwischenkreisspannung erzeugt wird. Diese Schalthandlungen werden durch
Pulsweitenmodulation derart gesteuert, dass an den Motorklemmen eine Spannung anliegt,
die in ihrem Frequenzspektrum die gewünschte Amplitude bei der gewünschten
Grundfrequenz enthält.
Neben vielen Vorteilen besitzt die standardmäßige Ausführung eines drehzahlveränderlichen
Antriebes den Nachteil, dass das Frequenzspektrum der Motorspannung neben der
gewünschten Grundfrequenz auch Oberschwingungen enthält, die beträchtliche Amplituden
bei hohen Frequenzen besitzen. Diese hochfrequenten Spannungsanteile führen zu
hochfrequenten Strömen im Motor. Zur Wandlung der elektrischen Energie an den
Motorklemmen in mechanische Energie an der Welle trägt jedoch nur der grundfrequente
Stromanteil bei ([19], [80]). Die hochfrequenten Anteile im Motorstrom hingegen erzeugen
lediglich Verluste im Motor, die dessen Ausnutzung reduzieren.
Ein weiterer Nachteil der gepulsten Umrichterausgangsspannung besteht darin, dass die
hohe Spannungssteilheit die Isolation des Motors in erhöhter Weise beansprucht ([10], [29]).
Dies ist insbesondere dann von Nachteil, wenn ein Antrieb vom Betrieb am starren Netz auf
einen drehzahlveränderlichen Antrieb umgerüstet werden soll, ohne den Motor zu ersetzen.
Die für den Netzbetrieb konzipierten Motoren sind häufig nicht in der Lage, die hohe
Spannungssteilheit des Umrichters zu verkraften, so dass ein Motoraustausch erforderlich
wird.
Ein dritter Nachteil der gepulsten Umrichterspannung betrifft die Verkabelung zwischen
Umrichter und Motor. Mitunter werden an dieser Stelle sehr lange Leitungen erforderlich.
Dies ist beispielsweise in der chemischen Industrie anzutreffen. Dort sind häufig sehr
großflächige, weitläufige Anlagen anzutreffen, bei denen die Frequenzumrichter in
klimatisierten Räumen zentral angeordnet sind, während sich die Motoren weit entfernt in der
Anlage befinden. In diesem Fall fließen durch die unvermeidbaren Kapazitäten der
7
Motorleitungen zu einem Kabelschirm oder Bezugserde nicht zu vernachlässigende Ströme,
die den Wechselrichter des Umrichters thermisch belasten. In der Praxis ist daher für die
Frequenzumrichter eine maximal zulässige Länge der anschließbaren Motorleitungen
definiert [116]. Darüber hinaus ist für die gepulsten Spannungen der Einsatz geschirmter
Motorleitungen erforderlich, um unzulässige Beeinflussungen anderer Geräte zu verhindern.
Diese geschirmten Motorleitungen sind deutlich teurer als die ungeschirmte Variante. Zudem
trifft auch hier der Sachverhalt zu, dass bei der Umrüstung eines Antriebes am starren Netz
auf einen drehzahlveränderlichen Antrieb die vorhandenen Motorkabel gegen geschirmte
Motorleitungen ersetzt werden müssen, wobei der Installationsaufwand erheblich sein kann.
All diese Argumente haben in der Vergangenheit dazu geführt, dass in einigen
Anwendungen, z.B. in der chemischen Industrie, sogenannte Sinusfilter am Ausgang des
Frequenzumrichters eingesetzt werden. Diese Sinusfilter filtern die hochfrequenten
Spannungsanteile aus der Motorspannung aus, so dass eine sinusförmige Spannung an den
Motorklemmen vorliegt. Zu diesem Zweck muss die Eckfrequenz des Sinusfilters zwischen
der gewünschten Grundfrequenz des Antriebes und der Schaltfrequenz des Wechselrichters
liegen. Die oben genannten Schwierigkeiten können dann reduziert oder ganz behoben
werden.
Der Nachteil dieser Lösung besteht darin, dass bei heute üblichen standardmäßigen
Schaltfrequenzen von 1 - 4 kHz der Sinusfilter aufgrund seiner niedrigen Eckfrequenz eine
großvolumige und teuere Komponente darstellt. Die mögliche Schaltfrequenz des
Wechselrichters wird durch die Schaltverluste begrenzt und sinkt mit steigender Spannung
des Antriebssystems, weil Halbleiterbauelemente mit hoher Sperrspannung besonders hohe
Schaltverluste verursachen.
Das Ziel dieser Arbeit besteht darin, Lösungsmöglichkeiten für ein Umrichterleistungsteil zu
erarbeiten, das im Vergleich zu heute mit erhöhter Schaltfrequenz arbeitet, so dass die
Eckfrequenz und damit der Aufwand für den Sinusfilter reduziert werden kann. Zu diesem
Zweck werden in dem ersten Teil der Arbeit unterschiedliche Halbleiterlösungen bzgl. einer
Dimensionierung des Motorwechselrichters miteinander verglichen, wobei ein besonderes
Augenmerk auf der Verwendung von Bauelementen aus dem Halbleitermaterial
Siliziumkarbid liegt. Im zweiten Teil der Arbeit werden die Realisierung des Sinusfilters und
dessen Rückwirkungen auf den Umrichter diskutiert.
Die erarbeiteten Ergebnisse werden an einem Demonstratorumrichter verifiziert. Die
gewählte Schaltungstopologie des Demonstratorumrichters ist in Abbildung 2 dargestellt:
690VNetz
EMV
Filter
Netz
filter
Netzstromrichter
ZK
Motorstromrichter
SinusAusgangsfilter
Motorleitungen
und Motor
M
Abbildung 2: Topologie des Demonstratorumrichters
Weil die Schwierigkeiten der hohen Schaltfrequenz des Wechselrichters insbesondere bei
hoher Anschlussspannung des Versorgungsnetzes auftreten, soll der Demonstrator für eine
Anschlussspannung von 690V konzipiert werden. Als Nennleistung des Demonstrators wird
18,5kW gewählt, was im mittleren Leistungsbereich heutiger Umrichterreihen liegt, so dass
die Ergebnisse möglichst gut auf niedrigere und höhere Leistungen übertragen werden
8
können. Die Ausführung der netzseitigen Umrichtertopologie ist für die Dimensionierung des
motorseitigen Wechselrichters und des Sinus-Ausgangsfilters von untergeordneter
Bedeutung, so dass sie im weiteren Verlauf der Arbeit nicht weiter betrachtet, sondern nur an
dieser Stelle kurz erläutert wird:
Als netzseitige Schaltungstopologie wird eine rückspeisefähige, unter dem Begriff
„Fundamental Frequency Front End“ (F3E) [95] bekannte Schaltungsanordung verwendet,
die den Ansatz der Arbeit nach einer kompakten Gesamtlösung unterstützt. Diese
Schaltungsanordnung verwendet auf der Netzseite einen aktiven Gleichrichter aus IGBTs
und Dioden, wobei die IGBTs nur mit der Frequenz des Netzes (z.B. 50Hz) getaktet werden
und somit kaum Schaltverluste anfallen. Wegen dieser geringen Schaltfrequenz sind die
Halbleiter des netzseitigen Gleichrichters auf optimales Durchlassverhalten ausgelegt; der
Einsatz von Schottkydioden als Freilaufdioden wäre im netzseitigen Gleichrichter deshalb
nicht sinnvoll. Als passive Komponenten benötigt diese netzseitige Umrichtertopologie
Wechselspannungskondensatoren auf der Netzseite, die in Verbindung mit der Induktivität
des Netzes einen Netzfilter bilden. Im Gegensatz zu der klassischen Topologie des
Spannungszwischenkreisumrichters
entfällt
eine
netzseitige
Drossel.
Der
Gleichspannungszwischenkreis
wird
mit
minimaler
Kapazität,
im
Fall
des
Demonstratorumrichters mit 10µF, ausgeführt. Diese Kapazität dient nicht wie im klassischen
Spannungszwischenkreisumrichter der Energiespeicherung, sondern lediglich der
Begrenzung von Schaltüberspannungen des Wechselrichters. Der Verlauf der
Zwischenkreisspannung zeigt nicht einen konstanten Wert, sondern weist charakteristisch
einen Wechselspannungsanteil mit der sechsfachen Frequenz des speisenden Netzes auf.
Der Netzstrom besteht in erster Näherung aus 120° Stromblöcken, in denen bei konstanter
Leistungsentnahme der Motorseite ebenfalls Frequenzanteile mit der sechsfachen
Netzfrequenz enthalten sind. Für tiefer gehende Ausführungen zum Betriebsverhalten der
netzseitigen Fundamental Frequency Front End Umrichtertopologie wird auf die Literatur
([43], [95]) verwiesen.
9
2 Halbleiterbauelemente des motorseitigen
Wechselrichters
In diesem Kapitel soll die Dimensionierung und Optimierung der Halbleiterbauelemente für
den motorseitigen Wechselrichter vorgenommen werden. Wesentliche Komponenten des
Motorwechselrichters sind die IGBT-Chips, die Freilaufdiodenchips und der Modulaufbau.
2.1 Der IGBT
Im ersten Schritt soll ein geeigneter aktiver Halbleiterschalter für den Motorwechselrichter
ausgewählt werden. In der praktischen Anwendung hat sich für Netzanschlussspannungen
zwischen 230V und 690V der IGBT als alleinige Halbleiterstruktur durchgesetzt ([80], [124]).
Entscheidend für die Bewertung eines IGBT ist der Kompromiss zwischen
Durchlassverlusten und Abschaltverlusten.
Dieser Kompromiss wird mit steigender
Sperrspannung eines Bauelements immer schwieriger, da bei angenommener gleich
bleibender Durchlassspannung die erforderliche gespeicherte Ladung in der schwach
dotierten Mittelschicht quadratisch ansteigen muss [15]. Da im vorliegenden Fall ein
Umrichter mit einer Ausgangsspannung von 690Vac entwickelt werden soll, sind IGBTs mit
einer zulässigen Sperrspannung von 1700V erforderlich, bei denen dieser Kompromiss eine
noch stärkere Rolle spielt als bei 1200V-Bauelementen. Dies ist der Grund dafür, dass 690VUmrichter heute in der Regel mit geringerer Schaltfrequenz betrieben werden als 400VUmrichter.
Die heute verfügbaren wesentlichen IGBT-Technologien für 1700V Sperrspannung sind
Trench-IGBTs und planare IGBTs ([24], [65], [66], [124]).
2.1.1 Trench-IGBT
Der schematische Aufbau der Halbzelle eines Trench-IGBTs sowie die zugehörige
Ladungsträgerverteilung im Durchlasszustand sind schematisch in Abbildung 3 gezeigt.
Der Trench-IGBT zeichnet sich vor allem durch seine guten Eigenschaften im
Durchlassverhalten
aus.
Dieses
wird
durch
die
verhältnismäßig
hohe
Ladungsträgerüberschwemmung erreicht. Die Injektion der Minoritätsladungsträger erfolgt
beim IGBT ausschließlich aus dem p+-Gebiet der Collectorseite (das emitterseitige p-Gebiet
ist durch den Inversionskanal von dem emitterseitigen n+-Gebiet zu dem schwach dotierten
n--Mittelgebiet überbrückt), deshalb nimmt die Konzentration der freien Ladungsträger in der
n--Mittelzone von der Collectorseite zum emitterseitigen pn-Übergang ab. Allerdings stauen
sich beim Trench-IGBT im Bereich unter dem Trench-Gate die freien Ladungsträger, weil die
Löcher durch die schmale Ausführung des Emitterbereiches nicht ungehindert abfließen
können. Abhängig von der konkreten geometrischen Ausführung des Bereiches zwischen
den Trench-Gates kann dadurch im Bereich unter dem Trench-Gate die Konzentration der
freien Ladungsträger verhältnismäßig hoch gehalten oder im Vergleich zum tiefer liegenden
n- Gebiet sogar wieder angehoben werden, wodurch die gute Durchlasseigenschaft des
Trench-IGBTs erreicht wird. Der Nachteil der hohen gespeicherten Ladung liegt in erhöhten
Abschaltverlusten, weil die gespeicherte Ladung beim Abschalten ausgeräumt werden muss.
10
A
B
G
x
E
x
Inversionskanal
n+
n,p
n+
n,p
p
p
Elektronen
n˜ p
n˜ p
n+
n+
n+
p+
p+
p+
n-
Löcherinjektion
C
A’
A - A’
B - B’
B’
Abbildung 3: Trench-IGBT Struktur und Ladungsträgerverteilung im Durchlasszustand entlang
den Linien A-A’ und B-B’
Die Trench-Technologie für IGBTs ist verhältnismäßig neu. Sie wird heute von den meisten
Herstellern für Standard-IGBTs der aktuellen Chipgeneration eingesetzt. Diese StandardIGBTs sind für eine Schaltfrequenz von ca. 4kHz bei 1200V-IGBTs und für eine
Schaltfrequenz von ca. 1,5kHz für 1700V-IGBTs optimiert.
2.1.2 Planarer IGBT
Alternativ zum Trench-IGBT sind planare IGBTs verfügbar. Die Planarstruktur war vor
Einführung
der
Trench-Struktur
bei
IGBTs
dominant.
Die
Struktur
und
Ladungsträgerverteilung eines solchen IGBTs sind schematisch in Abbildung 4 gezeigt.
11
x
A
E
G
n+
p
p
n,p
n+
Elektronen
Inversionskanal
n≈p
n-
n+
Löcherinjektion
p+
n+
p+
C
A - A’
A’
Abbildung 4: Planarer IGBT Struktur und Ladungsträgerverteilung im Durchlasszustand
entlang der Linie A-A’
Der planare IGBT zeichnet sich durch sehr gutes Abschaltverhalten aus, kann aber die
Durchlasswerte des Trench-IGBT nicht erreichen, da insbesondere im Bereich des
emitterseitigen pn-Überganges weniger freie Ladungsträger vorhanden sind und die
Zelldichte weniger hoch realisiert werden kann.
Bei beiden Strukturen besteht nun die Möglichkeit, durch die Dotierung des p+Collectorgebietes und des n+-Bufferlayers die Ladungsträgerverteilung genau einzustellen.
Zwei typische IGBTs der jeweiligen Technologie für 1700V/50A (Infineon) besitzen die
folgende Kennwerte ([54], [56]):
Bezeichnung
Durchlassspannung bei Abschaltverluste
Nennstrom
Technologie
FS50R17KE3
FS50R17KS4F
2,4V
4,9V
trench
planar
15,5mWs
7mWs
Tabelle 1: Durchlassspannung und Abschaltverluste verschiedener IGBTs
Diese Datenblattwerte, insbesondere die Abschaltverluste, sind als Richtwerte zum Vergleich
der Technologien zu verstehen. Bei der Anwendung im Umrichter sind diese Verluste stark
von der Ansteuerung und dem Aufbau des Leistungsteils abhängig, so dass sie an einem
Demonstrator messtechnisch erfasst werden müssen.
12
uce_planar
ic_trench
kV
kV
A
ic_planar
uce_trench
A
kV
kV
A
A
1.2
30
1.2
30
1.0
25
1.0
25
0.8
20
0.8
20
0.6
15
0.6
15
0.4
10
0.4
10
0.2
5
0.2
5
0.0
0
0.0
0
-0.2
-5
-0.2
-5
29
30
31
32
33
34
µs
Abbildung 5: Abschaltverhalten des schnellen planaren IGBT und des Trench-IGBTs
In Abbildung 5 sind das Abschaltverhalten des schnellen planaren IGBTs und des TrenchIGBTs vergleichend dargestellt. Die Farben magenta und rot zeigen die Collector-EmitterSpannung und der Collectorstrom des Trench-IGBT, schwarz und blau die äquivalenten
Messkurven des planaren IGBT. Die in Tabelle 1 zu erkennende Tendenz wird durch die
Messung bestätigt. Ursache für die erhöhten Abschaltverluste des Trench-IGBTs ist die
höhere Anzahl gespeicherter Ladungsträger, die beim Abschalten als Tailstrom zu erkennen
sind.
Aus dieser Messung kann die Schlussfolgerung gezogen werden, dass IGBTs in TrenchTechnologie für niedrige Schaltfrequenz zu bevorzugen ist, während der planare IGBT für
hohe Schaltfrequenz das bessere Verhalten erwarten lässt. Da in der vorliegenden Arbeit mit
erhöhter Schaltfrequenz gearbeitet wird, stellen planare IGBTs die bevorzugte Variante dar.
Im weiteren Verlauf der Arbeit wird deshalb mit planaren IGBTs gearbeitet.
2.1.3 Ansteuerbedingungen beim Abschalten des IGBT
Für die Schaltgeschwindigkeit beim Abschalten des IGBT sind mehrere Kriterien zu
berücksichtigen, die im Folgenden kurz erläutert werden sollen:
13
2.1.3.1 Maximale Überspannung
Aus der im Kommutierungskreis unvermeidlichen Streuinduktivität und der Forderung, dass
die beim Abschalten auftretende Überspannung am IGBT dessen maximale Sperrspannung
Usmax nicht überschreiten darf, ergibt sich:
U CE max = U zk + Ls
di
≤ U s max
dt
(1)
Bei dem vorliegenden Demonstratorumrichter befinden sich IGBT und Diode in einem
Halbleitermodul. Die durch den inneren Aufbau bedingte Streuinduktivität ist im Datenblatt
angegeben, sie beträgt 30nH [56]. Zu dieser Streuinduktivität addieren sich noch die
Streuinduktivität des Zwischenkreiskondensators und der Leistungsverschienung. Der
Zwischenkreiskondensator ist bei der verwendeten F3E-Topologie als Folienkondensator
realisiert.
Dieser
besitzt
eine
Eigeninduktivität
von
30nH
[30].
Die
Zwischenkreisverschienung wird bei dem Demonstratorumrichter als mehrlagige Leiterplatte
ausgeführt, wobei die stromführenden Kupferflächen zum positiven und negativen
Zwischenkreisanschluss mit so geringem Abstand wie möglich ausgeführt werden. In
Summe wird im Demonstrator eine Streuinduktivität von 100nH für den Kommutierungskreis
erreicht. Bei einer maximalen Zwischenkreisspannung von 1200V und einer maximalen
Halbleitersperrspannung von 1700V ergibt sich eine zulässige Überspannung von 500V. Für
die zulässige Stromsteilheit ergibt sich somit nach Gl. (1):
U
− U zk
di
500V
=≤ smax
=
dt
Ls
100nH
(2)
Die maximal zulässige Stromsteilheit beträgt somit 5kA/µs. Bei einem maximalen Strom von
100A bedeutet dies eine Stromfallzeit von 20ns. Derart schnelle Stromflanken können auch
bei sehr schneller Ansteuerung der vorgestellten IGBTs nicht erreicht werden. Deshalb stellt
das Kriterium der maximal zulässigen Überspannung im vorliegenden Fall keine Begrenzung
der Schaltgeschwindigkeit dar.
2.1.3.2 Abschaltfestigkeit im Kurzschlussfall
Ein weiteres Kriterium für eine Begrenzung der Schaltgeschwindigkeit ist die
Abschaltfestigkeit im Kurzschlussfall [80]. Dieses Kriterium beinhaltet zwei unterschiedliche
technische Hintergründe:
Zum einen darf wiederum die maximal zulässige Überspannung nicht überschritten werden.
Gegenüber Kapitel 2.1.3.1 verschärft sich die Anforderung, weil der abzuschaltende Strom
nun nicht mehr von den Betriebspunkten des Umrichters abhängt, sondern von dem
Entsättigungsstrom der IGBTs, welcher typischerweise den fünf- bis achtfachen Wert des
IGBT-Nennstromes beträgt.
Zum anderen bildet der dynamische Avalanche eine Grenze für die Abschaltfestigkeit.
Ausgehend von der in Abbildung 4 erläuterten Ladungsträgerverteilung im statischen
Durchlasszustand vor dem Abschalten wird diese Problematik in Abbildung 6 anhand der
Ladungsträgerverteilung und dem elektrischen Feldverlauf während des Abschaltvorgangs
veranschaulicht:
14
x
x
x
n+
n+
p
p
n+
Emax
Emax
p
n,p,E
n,p,E
n,p
w1
n˜ p
n-
n-+p*
w
n˜ p
n-
n˜ p
n+
n+
n+
p+
p+
p+
statischer
Durchlasszustand
Abschaltvorgang
statischer
Sperrzustand
Abbildung 6: Ladungsträgerverteilung und elektrisches Feld im IGBT in unterschiedlichen
Betriebspunkten
Im statischen Sperrzustand ist in der schwach dotierten Mittelschicht die Dichte der sehr
geringe freien Ladungsträger sehr gering (n, p << ND), der Feldgradient wird nach Gl. (9) (s.
Kap. 2.2.1) von der Grunddotierung der Mittelschicht bestimmt. Die in diesem
Betriebszustand von dem IGBT aufgenommene Sperrspannung kann nach Gl. (10)
berechnet werden und entspricht der Fläche unter der Kurve des elektrischen Feldes.
Während des Abschaltvorganges muss nun vom IGBT Sperrspannung aufgenommen
werden, während noch Strom durch den IGBT fließt. Im mittleren Bild von Abbildung 6 sind
die Verteilung der Ladungsträger und des elektrischen Feldes zu einem Zeitpunkt während
des Abschaltvorganges dargestellt. Der Gradient des elektrischen Feldes wird wiederum
durch die effektive Dotierung im Bereich des Feldes bestimmt. Allerdings addiert sich nun zu
der Grunddotierung in diesem Gebiet die Ladung der Löcher, durch die der über das
elektrische Feld fließende Strom getragen wird. Deshalb ergibt sich in dem Gebiet des
elektrischen Feldes ein steilerer Feldgradient. Da aber zu einem Zeitpunkt, in dem noch
Strom durch dem IGBT fließt, bereits die volle Zwischenkreisspannung aufgenommen
werden muss, steigt gegenüber dem statischen Sperrzustand die maximale elektrische
Feldstärke am pn-Übergang an. Gleichzeitig reduziert sich die effektive Basisweite des IGBT
von der gesamten Dicke w des schwach dotierten Mittelgebietes auf den Wert w1. Je
schneller die Spannung am IGBT ansteigt, desto stärker wirkt dieser Effekt.
Der dynamische Avalanche spielt grundsätzlich bei jedem Abschaltvorgang eine Rolle, er
wird jedoch umso kritischer, je höher der abzuschaltende Strom ist. Da im Kurzschlussfall
der Strom weit größer ist als in regulären Betriebspunkten des Umrichters, ist auch der
dynamische Avalanche im Kurzschlussfall am kritischsten.
Im Fall eines Umrichters mit integriertem Sinusfilter ist ein harter Kurzschluss für die IGBTs
am Umrichterausgang ausgeschlossen, da im Kurzschlusspfad immer mindestens eine
Filterdrossel liegt, die den Stromanstieg drastisch reduziert. Dadurch kann jeder externe
Kurzschluss vom Umrichter mit Hilfe der Ausgangsstrommessung erkannt werden. Eine
Abschaltung erfolgt somit bereits an der betriebsmäßigen Überstromschwelle und nicht erst
an dem Entsättigungsstrom der IGBTs.
15
Kurzschlussstelle
U
Uzk
V
W
UCU
UCV
Abbildung 7: Kurzschluss zwischen zwei Phasen am Umrichterausgang
Der Ausgangsstrom des Wechselrichters wird in der Filterdrossel gemessen. Im Fall eines
Kurzschlusses am Umrichterausgang nach Abbildung 7 treibt die Zwischenkreisspannung
einen Kurzschlussstrom in der Fehlerstelle, falls die Halbleiter dementsprechend
eingeschaltet sind. Im gezeigten Beispiel fließt ein Kurzschlussstrom, wenn in Phase U der
obere und in Phase V der untere IGBT eingeschaltet sind. Stromwandler nach dem Stand
der Technik sind in der Lage, innerhalb von Δt= 10µs einen Strommesswert zu liefern und
somit auch einen Kurzschlussstrom zu erkennen. Falls sichergestellt werden kann, dass ein
Betrag des Stromes deutlich über dem Nennstrom innerhalb dieser 10µs nicht auftreten
kann, kann ein hoher Kurzschlussstrom und somit eine hohe Belastung der Abschaltfähigkeit
der IGBTs ausgeschlossen werden.
Die Anstiegsgeschwindigkeit des Kurzschlussstromes hängt von dem Induktivitätswert der
Filterdrossel ab. Bei Umrichtern ohne Ausgangsfilter ist dieser Wert nahezu null, wodurch
der Kurzschlussstrom innerhalb von einer Mikrosekunde bis auf den Entsättigungsstrom der
IGBTs, etwa dem fünf- bis achtfachen Nennstrom der IGBTs, ansteigen kann. Dass bei
Umrichtern mit Sinusfilter der Stromanstieg wesentlich langsamer sein muss, zeigt folgende
Plausibilitätskontrolle:
Im bestimmungsgemäßen Betrieb wird der Umrichter mit seiner Schaltfrequenz getaktet.
Abhängig von dem Sollspannungswert während einer Modulationsperiode kann ein
Spannungszeiger nahezu die gesamte Zeitdauer der Modulationsperiode betragen. Für die
Plausibilitätskontrolle wird der Extremfall angenommen, dass ein Spannungszeiger für die
gesamte Dauer der Modulationsperiode konstant ist. Ist dies ein Spannungszeiger, der in
Phase U den oberen IGBT einschaltet und in Phase V den unteren IGBT, so ist die
Ausgangsspannung des Wechselrichters in diesem Fall identisch wie bei der beschriebenen
Kurzschlussbedingung. Sind zum Zeitpunkt dieser Modulationsperiode die Spannungen UCU
und UCV identisch (Nulldurchgang der verketten Motorspannung), so herrscht während der
gesamten Modulationsperiode der gleiche Zustand wie während des Kurzschlusses.
Die Induktivität des Sinusfilters ist mindestens so zu bemessen, dass der Ripplestrom in
diesem Betriebszustand nicht unzulässig groß wird. Auf genauere Dimensionierung der
Drossel wird in Kap. 3.2 eingegangen. Bei Schaltfrequenzen unter 100kHz ist die
Modulationsperiode länger als 10µs, so dass ein Kurzschlussstrom innerhalb von 10µs
maximal auf den Wert des Ripplestroms ansteigen kann. Der Ripplestrom muss von dem
IGBT bestimmungsgemäß beherrscht werden. Deshalb stellt ein Kurzschlussstrom innerhalb
von 10µs keine erhöhte Belastung gegenüber dem bestimmungsgemäßen Betrieb dar. Erst
bei Schaltfrequenzen über 100kHz könnte ein Kurzschlussstrom eine erhöhte Belastung
darstellen. Da zwischen betriebsmäßigem Strom und Entsättigungsstrom des IGBT in der
Praxis aufgrund der Halbleiterspezifikation ein großer Sicherheitsbereich von mindestens
einem Faktor 2 liegen muss, sind kritische Ströme erst bei noch höheren Schaltfrequenzen
plausibel.
16
Diese Erkenntnis hat weit reichende Konsequenzen für die Dimensionierung des IGBT. Sie
bedeutet, dass der IGBT in seiner Abschaltrobustheit nicht für kurzschlussfestes Verhalten
ausgelegt sein muss, da der im Kurzschlussfall zusätzlich fließende Strom unter dem
Nennstrom des Umrichters liegt. Dies ermöglicht Freiheiten in der Optimierung bezüglich
Schalt- und Durchlassverlusten gegenüber Umrichteranwendungen ohne integrierten
Sinusfilter.
Ein harter Kurzschluss an den Ausgangsphasen des Wechselrichters kann somit nur durch
einen internen Fehler im Umrichter erzeugt werden und nicht durch einen externen Fehler
seitens des Anwenders. In der Schutzphilosophie der heutigen Umrichter im Bereich
<100kW hat sich durchgesetzt, den Wechselrichter gegen interne Gerätefehler nicht zu
schützen, da diese bei geeignetem Umrichterdesign extrem selten auftreten. Diese
Schutzphilosophie soll als Stand der Technik auch in dem zu realisierende Demonstrator
verwendet werden, so dass auch von dieser Seite kein kurzschlussfestes IGBT-Design
erforderlich ist.
Damit ist auch das Abschaltverhalten im Kurzschlussfall kein Kriterium, das die
Schaltgeschwindigkeit begrenzt, lediglich die Abschaltfestigkeit im bestimmungsgemäßen
Betrieb ist zu gewährleisten.
2.1.3.3 Belastung der Komponenten der Potenzialtrennung
Ein weiterer Gesichtspunkt, der bei der Auswahl der Spannungssteilheit zu berücksichtigen
ist, ist die Belastung von Komponenten zur Potenzialtrennung. Diese Komponenten sind
erforderlich, um Steuersignale und Hilfsspannungsversorgungen auf dem jeweils
erforderlichen Potenzial zur Verfügung zu stellen. Eine typische Applikation ist in Abbildung 8
gezeigt:
Potenzialtrennung
DCP
Optokoppler
C1
µC
U, f
Steuer- UStA
satz
T1
Ansteuerschaltung
für T1
C2
U
SNTPrimär
seite
Transformator
T2
UU
DCN
Abbildung 8: Potenzialtrennung in einem Umrichter
Um den IGBT T1 ansteuern zu können, ist es erforderlich, an dessen Gate-Emitter-Strecke
eine definierte Spannungskurvenform zur Verfügung zu stellen. Von einem Referenzniveau
(z.B. dem negativen Anschluss DCN des Zwischenkreises, s. Abbildung 8) muss eine
bestimmte Energie zum Treiben der kapazitiven Last am Eingang des IGBT sowie eine
17
digitale Information, wann der IGBT ein- bzw. ausschalten soll, für jeden IGBT übertragen
werden. In Abbildung 8 wird für das Referenzniveau der negative Zwischenkreisanschluss
verwendet, die absolute Lage des Referenzniveaus ist für die dynamische Belastung der
potenzialtrennenden Bauteile jedoch beliebig, da die dynamische Belastung nur von der
Änderung von Potenzialen bestimmt wird.
Die Energie wird in den meisten Fällen durch ein Schaltnetzteil mit einem Transformator
übertragen. Die digitale Information kann durch verschiedene Komponenten wie
Optokoppler, Impulsübertrager, magneto-resistive Übertrager oder Lichtwellenleiter
übertragen werden. Als Stand der Technik hat sich im Bereich von Umrichtern der
Optokoppler als potenzialtrennendes Bauelement etabliert, da er kostengünstig ist, keinerlei
Einschränkungen bzgl. des zu übertragenden Aussteuergrades erfordert und seit vielen
Jahren im Feldeinsatz bewährt ist.
Alle potenzialtrennenden Bauteile besitzen aufgrund endlicher Ausdehnung und
vorgegebener Materialeigenschaften eine parasitäre Kapazität über die Potenzialtrennstelle
von ihrer Primär- zur Sekundärseite. In Abbildung 8 sind hierfür die Kapazitäten C1 und C2
eingetragen. Wechselt nun das Potenzial der Ausgangsphase U von DCN auf DCP bzw.
umgekehrt, so tritt diese Spannungsänderung nahezu unverändert auch an den
Kondensatoren C1 und C2 auf, da alle weiteren Kondensatoren, die C1 und C2 mit den
Potenzialen DCN bzw. U verbinden, Stützkondensatoren mit wesentlich höheren
Kapazitätswerten sind.
Durch diese Spannungsänderung muss in den Kapazitäten C1 und C2 ein Strom fließen, der
proportional zum Kapazitätswert und zur Spannungsänderung
von 10pF und einer Spannungssteilheit von 10
dUU
ist. Bei einer Kapazität
dt
kV
ergibt sich ein Strom von 100mA.
µs
Dieser kapazitive Störstrom kann zum einen die Funktionsweise des potenzialtrennenden
Bauelementes selbst beeinflussen. Im Fall eines Optokopplers kann es dazu führen, dass
dieser Strom in der Sendediode des Optokopplers fließt und zu einem unbeabsichtigten
Einschaltvorgang führt. Aus diesem Grund sollte die Sendediode eines Optokopplers im
ausgeschalteten Zustand immer direkt mit einem parallel geschalteten, nahe an den
Bauteilpins angeordneten Transistor kurzgeschlossen werden, der diesen Störstrom ohne
nennenswerten Spannungsabfall führen kann.
Zum anderen können die Störströme zu Fehlfunktionen in der IGBT-Ansteuerung oder der
primärseitigen Pulserzeugung führen. In einer Schaltung nach Abbildung 8 kann dies
anschaulich dargestellt werden:
18
Potenzialtrennung
DCP
Optokoppler
µC
U, f
P15
T1
D1
Steuer- UStA
satz
C1
UC1
R1
UR1
U
N15
IU
UU
T2
D2
DCN
Abbildung 9: Störung der Ansteuerung
In Abbildung 9 ist eine typische Halbbrückenschaltung dargestellt. Der Laststrom IU sei
negativ und T2 sei ausgeschaltet, der Laststrom fließe durch D1. T1 sei zunächst
eingeschaltet und wird nun abgeschaltet, um den Wechsel des Potenzials U vorzunehmen.
Das Abschalten von T1 bewirkt an UU keine Veränderung, da D1 weiterhin den Strom führt.
Lediglich der Optokoppler der Ansteuerung von T1 wird ausgeschaltet.
Nach Ablauf der Verriegelungszeit schaltet nun T2 ein. Der Laststrom kommutiert von D1 auf
T2, D1 nimmt Spannung auf. Der Spannungsanstieg an D1 bildet sich in gleicher Weise an
C1 ab. Die Spannung UC1 hat vor der Kommutierung das Potenzial der
Zwischenkreisspannung betragen, diese Spannung wird nun während der Kommutierung bis
auf 0 abgebaut. Dadurch fließt ein Strom von C1 in die Ansteuerschaltung von T1 hinein.
Der Optokoppler dieser Ansteuerschaltung ist ausgeschaltet, der Störstrom muss über R1
abfließen. Damit verursacht er über R1 einen Spannungsabfall UR1, der möglicherweise zu
einem fehlerhaften Einschalten von T1 führen und die Brückenschaltung zerstören kann.
Deshalb ist bei der Ausführung der Potenzialtrennung darauf zu achten, dass der
Spannungsabfall
an
R1
möglichst
klein
zu
halten
ist.
Da
die
Spannungsänderungsgeschwindigkeit hoch gewählt werden soll, um die Schaltverluste
gering zu halten, können folgende Maßnahmen getroffen werden:
a) Verwendung eines Optokopplers (oder eines anderen potenzialtrennenden
Bauelementes) mit geringer Koppelkapazität bzw. Schirmung: mit dieser Maßnahme
wird der Störstrom reduziert. In einer konkreten Anwendung sind geeignete
Optokoppler einzusetzen, allerdings sind geringe Koppelkapazitäten auch bei sehr
störfesten Optokopplern unvermeidbar [1].
b) Verwendung eines Optokopplers mit niederohmigem Ausgang: besitzt der Ausgang
des Optokopplers eine Gegentaktstufe, so wird der Widerstand R1 überflüssig, weil
der Optokoppler im ausgeschalteten Zustand aktiv gegen das negative
19
Versorgungspotenzial der Ansteuerschaltung von T1 schaltet und somit einen
niederohmigen Pfad für den Störstrom zur Verfügung stellt. Diese Maßnahme
reduziert nicht den Störstrom, sondern dessen Auswirkungen. Für die externe
Schaltung ist das Problem damit gelöst, allerdings muss im Optokoppler eine
geeignete Ansteuerung dieser Gegentaktstufe existieren; für die Anwendung besteht
jedoch der Vorteil, dass die dU/dt-Festigkeit eines solchen Optokopplers im
Datenblatt spezifiziert ist.
c) Stützung des Ausgangssignals des Optokopplers durch einen zusätzlichen
Kondensator: Wird R1 ein Kondensator parallel geschaltet, so kann dieser den
kurzzeitigen Störstrom führen, ohne dass an R1 ein unzulässig hoher
Spannungsabfall auftritt. Auch diese Maßnahme reduziert nicht den Störstrom selbst,
sondern dessen Auswirkung. Die in diesem zusätzlichen Kondensator gespeicherte
Energie wird bei jedem Schaltvorgang in Verlustwärme umgesetzt; der Widerstand R1
ist entsprechend auszulegen.
Neben möglichen Fehlfunktionen der Ansteuerung können hohe Störströme zu erhöhten
Abstrahlungswerten in der EMV-Messung führen.
Für sehr schnelle Optokoppler, die in Frequenzumrichtern standardmäßig verwendet
werden, ist ein sicherer Betrieb bis 15
kV
kV
spezifiziert. Deshalb soll der Wert von 15
für
µs
µs
den Demonstratorumrichter eingehalten werden. Auswirkungen der Schaltgeschwindigkeit
auf die Schaltverluste, die eine Motivation für höhere Schaltgeschwindigkeit darstellen
könnten, werden im folgenden Kapitel behandelt.
2.1.3.4 Verlustersparnis durch schnelles Schalten
Letztendlich entscheidet über die Attraktivität sehr schnellen Schaltens die mögliche
Verlusteinsparung, die dadurch erzielt werden kann.
In Abbildung 10 ist ein typischer Abschaltvorgang bei einem Strom von 23A und einer
Zwischenkreisspannung von 1000V dargestellt. Die Spannungsanstiegsgeschwindigkeit
beträgt 12
kV
. Es ist zu erkennen, dass auch bei dem in Abbildung 10 verwendeten IGBT
µs
mit niedrigem Tailstrom noch ca. 50% der Schaltverlustenergie im Tailbereich anfällt. Diese
Verlustenergie ist durch die Technologie des IGBT bestimmt und kann durch die Wahl der
Schaltgeschwindigkeit nicht reduziert werden [97], so dass durch schnelleres Schalten nur
50% der Abschaltverlustenergie für mögliche Reduzierungen zur Verfügung stehen.
Angesichts dieser Tatsache wurde für den Demonstratorumrichter entschieden, eine
maximale Spannungsanstiegsgeschwindigkeit von 15
kV
zu verwenden. Dieser Wert ist die
µs
Obergrenze, bei der noch standardmäßige Bauteile für die Potenzialtrennung eingesetzt
werden können. Darüber steigt mit höheren Schaltsteilheiten auch die Problematik bzgl.
elektromagnetischer Verträglichkeit (EMV), so dass 15
die Spannungssteilheit gewählt wurden.
20
kV
als geeigneter Kompromiss für
µs
uge
V
Uce
Ic
Es
kV
mWs
A
20
1.05
28
2.8
15
0.90
24
2.4
10
0.75
20
2.0
5
0.60
16
1.6
0
0.45
12
1.2
-5
0.30
8
0.8
-10
0.15
4
0.4
-15
0.00
0
0.0
-20
-0.15
-4
-0.4
29.5
30.0
30.5
31.0
µs
Abbildung 10: Schaltverlustenergie während eines Abschaltvorganges eines planaren IGBT
1700V/50A
2.1.4 Dynamische Sättigungsspannung
An dieser Stelle soll noch das Phänomen der dynamischen Sättigungsspannung erläutert
werden. Damit ist gemeint, dass ein IGBT beim Einschalten nicht unmittelbar nach der
Schaltflanke des Stromes als Durchlassspannung seinen stationären Wert erreicht, weil zu
diesem Zeitpunkt erst wenige gespeicherte Ladungsträger in der schwach dotierten
Mittelschicht vorhanden sind. Der Aufbau der stationären, in Abbildung 3 und Abbildung 4
gezeigten Ladungsträgerverteilung erfordert eine gewisse Zeit [15]. Während dieses Aufbaus
der Ladungsträgerüberschwemmung zeigt der IGBT erhöhte Durchlassverluste. Dieses
Phänomen ist bei niedriger Schaltfrequenz wenig relevant, da der Zustand, dass der IGBT
einschaltet, verhältnismäßig selten vorkommt. Bei hoher Schaltfrequenz ist das Phänomen
jedoch zu berücksichtigen, da es entsprechend häufiger vorkommt und der Zeitraum des
Einschaltens gegenüber der gesamten Leitdauer ein größeres Gewicht bekommt.
In Abbildung 11 ist der Einschaltvorgang eines schnellen planaren IGBT 1700V/50A gezeigt.
Der Test zeigt einen Betrieb bei kleiner Zwischenkreisspannung und großem Laststrom.
Durch die kleine Wahl der Zwischenkreisspannung kann die Spannung am IGBT im unteren
Bereich sehr gut aufgelöst werden.
21
uce
ic
V
A
40
100
38
95
36
90
34
85
32
80
30
75
28
70
26
65
24
60
22
55
20
50
18
45
16
40
14
35
12
30
10
25
8
20
6
15
4
10
2
5
0
0
-2
-5
-4
-10
80
90
100
110
µs
Abbildung 11: Dynamische Sättigung des planaren IGBT 1700V/50A beim Einschalten
Es ist zu erkennen, dass nach der schnellen Einschaltflanke bei ca. 82 µs der IGBT noch ca.
5µs benötigt, um seine stationäre Durchlassspannung zu erreichen. Dass der stationäre
Wert in Abbildung 11 bei ca. 87µs erreicht wird, ist daran zu erkennen, dass die
Durchlassspannung am IGBT nach diesem Zeitpunkt wieder ansteigt, was auf den
steigenden Laststrom zurückzuführen ist.
Die Wirkungsweise der dynamischen Sättigungsspannung ist direkt in einem MessAuswertungsprogramm für Halbleiterverluste im Umrichterbetrieb schwer zu berücksichtigen,
da bei einer Zwischenkreisspannung von ca. 1000V der Bereich der letzten 20V nur schwer
zu erkennen ist. Deshalb soll sie durch eine geeignete, einfache Modellbildung nachgebildet
werden. Diese Modellvorstellung basiert auf einem schematisch gezeichneten Verlauf der
IGBT-Collectorspannung nach Abbildung 12:
22
UCE
UCE1
UCEsat
t
t0
t1
tx
t2
Abbildung 12: Schematischer Einschaltvorgang eines IGBT
Während des gesamten Einschaltvorganges wird der Laststrom des kommutierenden
Umrichterzweiges als konstant angenommen; er ist deshalb in Abbildung 12 nicht
eingezeichnet.
Der Abbau der Collectorspannung während des Einschaltvorganges findet im Intervall [t0;
t1]statt. Zum Zeitpunkt t1 erreicht die Collectorspannung des IGBT jedoch noch nicht den
Wert UCEsat, sondern nur den Wert UCE1. Man beachte hierbei die gestreckte Darstellung der
Ordinate.
Der Zeitpunkt tx bezeichnet das Ende des Intervalls, innerhalb dem die Schaltverluste
ermittelt werden. Die Wahl dieses Zeitpunktes ist sehr wichtig, um zuverlässige Aussagen
über Schaltverluste machen zu können. Wird tx zu früh gewählt, beispielsweise tx < t1, so
werden die Schaltverluste als zu gering bewertet. Wird tx zu spät gewählt, so werden bei den
Schaltverlustenergien zusätzlich Durchlassverlustenergien mit bewertet. Diese können mit
E add 1 = U CEsat I Last (t x − t 0 )
(3)
berechnet werden und können für große Werte von tx beträchtlich werden.
Üblicherweise wird tx = t1 gewählt. In diesem Fall wird jedoch der Verlustenergieanteil der
dynamischen Sättigungsspannung nicht berücksichtigt. Dieser beträgt
t2
E dyn = ∫ ((U CE (t ) − U CEsat ) I Last ) dt
(4)
t1
Um dies auszugleichen, kann der Zeitpunkt tx verschoben werden. Im einfachsten Fall kann
für tx = t2 gewählt werden. Allerdings hat diese Lösung wieder den Nachteil, dass eine
zusätzliche Durchlassverlustenergie
E add 2 = U CEsat I Last (t 2 − t 0 )
(5)
mit berechnet wird und die Messergebnisse verfälscht.
23
Idealerweise wird der Zeitpunkt tx so gewählt, dass die Gleichung
t2
∫ (U
CE
(t ) − U CEsat ) dt = U CEsat (t x − t 0 )
(6)
tx
erfüllt ist. In diesem Fall wird der nach Beendigung des Integrationsintervalls anfallende
Verlustenergieanteil der dynamischen Sättigungsspannung den zuvor bei der
Schaltverlustenergie zuviel gewerteten Anteil an Durchlassenergie kompensieren.
2.2 Die Freilaufdiode
2.2.1 Die Si-pn-Diode
In heute üblichen Frequenzumrichtern werden als Freilaufdioden im Motorwechselrichter bei
Anschlussspannungen ab 230Vac nahezu ausschließlich pin-Leistungsdioden eingesetzt.
x
A
p+
p+
n,p
n˜ p
n-
n+
n+
K
Abbildung 13: pin-Leistungsdiode, Struktur und Ladungsträgerverteilung
Abbildung 13 sind schematisch die Struktur und die Ladungsträgerverteilung im Leitzustand
für eine pn-Leistungsdiode dargestellt ([96], [109]). Wie auch beim IGBT muss bei der
Dimensionierung eines realen Bauelements ein Kompromiss zwischen Durchlassspannung
und Abschaltverlusten gefunden und für den Anwendungsfall optimiert werden.
24
Die Durchlassspannung einer pn-Leistungsdiode setzt sich im Wesentlichen aus zwei
Anteilen zusammen:
Den ersten Anteil bezeichnet man als Schwellenspannung. Dieser Anteil ist in erster
Näherung unabhängig von dem in der Diode fließenden Strom. Er ergibt sich durch
Diffusionsspannungen an dem p+n und am nn+-Übergang der Diode und hängt von den
Dotierungen der einzelnen Gebiete ab. Nach [109] kann die Schwellenspannung einer pnDiode berechnet werden durch
U th =
k T ⎛⎜ p l nr
ln
q ⎜⎝ ni 2
⎞
⎟,
⎟
⎠
(7)
wobei pl und nr die Anzahl der injizierten Ladungsträger aus dem p+ bzw. n+- Gebiet in die
schwach dotierte Mittelschicht darstellen. Die Schwellenspannung realer Si-Leistungsdioden
liegt etwa bei 0,8V.
Der zweite Anteil der Durchlassspannung einer pn-Diode wird als Driftzonenspannung
bezeichnet. Er repräsentiert den Spannungsabfall über der schwach dotierten Mittelschicht
der Diode.
U Drift
w2
=
(µ p + µn ) Q I
(8)
In dieser Gleichung kann der Zusammenhang der Speicherladung Q mit der Driftspannung
UD sehr anschaulich dargestellt werden. µp und µr bezeichnen die Beweglichkeit der Löcher
bzw. Elektronen und sind Materialkonstanten des Halbleitermaterials. Soll der
Driftspannungsabfall für einen gegebenen Strom I konstant bleiben, so muss die
Speicherladung Q quadratisch mit der Dicke der Mittelschicht w ansteigen. Die Dicke der
Mittelschicht hängt bei sperrgepoltem pn-Übergang wiederum unmittelbar mit der
Sperrfähigkeit der Diode zusammen:
A
p+
E
n-
w
n+
x
K
Abbildung 14: Feldverlauf in der pn-Leistungsdiode im Sperrzustand
25
Bei sperrgepoltem pn-Übergang ergibt sich der in Abbildung 14 gezeichnete Feldverlauf mit
der Beziehung
dE q N ( x )
=
dx
ε
für N(x)=const.
(9)
Hierbei ist angenommen, dass die Dichte der freien Ladungsträger in der Raumladungszone
so gering ist, dass diese bei der Berechnung des elektrischen Feldes vernachlässigt werden
können.
Die maximale Sperrspannung, die von der Diode aufgenommen werden kann, kann unter
der Annahme, dass das Maximum der E(x)-Verteilung gerade den Wert der
Durchbruchfeldstärke Ekrit erreicht, durch Integration des elektrischen Feldes über die
Bauelementdicke errechnet werden. Da der Feldgradient in den hoch dotierten Gebieten p+
und n+ wesentlich höher ist als in der schwach dotierten Mittelschicht, errechnet sich die
Sperrspannung zu
w
U s max = ∫ E ( x )dx
(10)
0
Anschaulich kann die Sperrspannung der Diode als Fläche unter der Kurve des elektrischen
Feldes gesehen werden. Soll nun die Durchbruchspannung eines Bauelementes erhöht
werden, so erfordert dies eine Vergrößerung der Dicke w des schwach dotierten
Mittelgebietes, weil einer Erhöhung der Feldstärke E physikalische Grenzen gesetzt sind, da
die maximale Durchbruchfeldstärke Ekrit des spezifischen Halbleitermaterials nicht
überschritten werden darf.
Um die Durchlassspannung einer Diode trotz steigender Sperrfähigkeit konstant zu halten,
bedeutet dies gemäß Gl. (8), dass mit steigender Durchbruchspannung Usmax einer Diode
wegen der näherungsweise linearen Zunahme der Dicke w ihrer Mittelschicht die in der
Diode gespeicherte Ladung Q quadratisch zunehmen muss. Vernachlässigt man die
Ladungsträgerrekombination während des Abschaltvorgangs, so kann die Speicherladung
bei jedem Abschaltvorgang der Diode messtechnisch erfasst werden:
I
t0
t1
t2
t
Q
Abbildung 15: Schematischer Strom beim Abschalten einer pin-Diode
26
Beim Abschaltvorgang muss die in der Diode gespeicherte Ladung Q ausgeräumt werden,
damit die Diode Spannung aufnehmen kann. Dieser Vorgang ist als Diodenrückstrom
sichtbar, wobei das Integral des Rückstromes die Speicherladung Q darstellt. Da die Diode
ab dem Zeitpunkt t1 Spannung aufnimmt, führt dieser Diodenrückstrom zu Abschaltverlusten
in der Diode. Zusätzlich addiert sich der Diodenrückstrom zu dem Laststrom für den
einschaltenden IGBT, so dass er in dem IGBT zu einer Erhöhung der Einschaltverluste führt.
Im vorliegenden Fall ist eine Diode für eine maximale Sperrspannung von 1700V
erforderlich. Eine solche Diode ist standardmäßig als 50A-Chip verfügbar. Zusätzlich zu
dieser Diode wurde noch ein zweiter Si-pn-Diodenchip getestet, der zunächst nur als
Labormuster verfügbar ist, jedoch für höhere Schaltfrequenz optimiert wurde und daher
möglicherweise eine interessante Alternative darstellt.
Die Durchlassspannung der Standarddiode wurde gemessen:
Kennlinie Diode Si
40
35
30
I [A]
25
25 °C
125 °C
20
15
10
5
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
U [V]
Abbildung 16: Durchlasskennlinie der Si-Standarddiode
Für die schnelle Si-Diode wurde folgende Durchlasskennlinie gemessen:
Kennlinie Diode SiFast
40
35
30
I [A]
25
25 °C
125 °C
20
15
10
5
0
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
U [V]
Abbildung 17: Durchlasskennlinie der schnellen SiFast-Diode
27
1.8
2
Bei beiden Dioden ist der für pn-Dioden typische negative Temperaturkoeffizient der
Durchlassspannung zu erkennen. Die Kennlinien bei 125°C zeigen keinen allzu großen
Unterschied. Die Durchlassspannung der schnellen Diode ist nur geringfügig höher als die
der Standarddiode. Ein größerer Unterschied ist bei 25°C sichtbar. Dies legt die Vermutung
nahe, dass vor allem bei Raumtemperatur die Speicherladung der schnellen Diode deutlich
geringer ist.
Für einen Vergleich der beiden Dioden ist neben den statischen Eigenschaften auch das
dynamische Verhalten ausschlaggebend. Um dieses zu charakterisieren, ist eine
vergleichende Messung der beiden Dioden in Abbildung 18 dargestellt:
Spannung_Si
Spannung_SiFast
kV
Strom_Si
Strom_SiFast
kV
A
A
1.25
80
1.25
80
1.00
60
1.00
60
0.75
40
0.75
40
0.50
20
0.50
20
0.25
0
0.25
0
0.00
-20
0.00
-20
-0.25
-40
-0.25
-40
189.5
190.0
190.5
191.0
191.5
192.0
192.5
193.0
µs
Abbildung 18: Abschaltverhalten der Standard-Si-Diode und der schnellen Si-Diode, 125°C
Bei diesem Versuch wurden beide Dioden mit dem gleichen IGBT abkommutiert. Die
Zwischenkreisspannung beträgt ca. 1100V, dies ist ein Wert in der Nähe der oberen
zulässigen Zwischenkreisspannungsgrenze eines 690V-Umrichters. Die Dioden wurden auf
eine Temperatur von 125°C vorgeheizt, um einen realistischen Belastungszustand
nachzubilden. Der Vorstrom durch die Dioden vor dem Abschaltvorgang betrug ca. 35A.
In Abbildung 18 ist zu erkennen, dass die Speicherladung der schnellen Diode geringer ist
als die der Standarddiode. Dabei reduziert sich jedoch nicht die Rückstromspitze, sondern
vielmehr der Rückstrom im hinteren Bereich der Speicherzeit. Damit zeigt die schnelle Diode
nach der Rückstromspitze einen deutlich schnelleren Rückgang des Stromes als die
Standarddiode. Da diese Stromsteilheit nach der Rückstromspitze in Verbindung mit der
Streuinduktivität des Kommutierungskreises die Überspannung an der Diode bestimmt, ist
28
die schnelle Diode deutlich stärker belastet als die Standarddiode. Der Rückstrom selbst
beträgt bei beiden Dioden etwa das Doppelte des Vorstromes der Diode. Dies ist ein
verhältnismäßig hoher Wert, wenn man bedenkt, dass der Vorstrom in Abbildung 18 ca. 70%
des
Diodennennstromes
beträgt.
Dies
ist
zu
erklären
durch
die
hohe
Sperrspannungsfestigkeit der Diode von 1700V und durch die hohe Schaltgeschwindigkeit,
die erforderlich ist, um geringe Gesamtschaltverluste zu erreichen.
Die Speicherladung ist ein Maß für die Verlustenergie, die in der Diode bei dem
Schaltvorgang umgesetzt wird. Für diese Verlustenergie gilt:
E offd = ∫ U d (t ) I d (t ) dt
(11)
Da der Verlauf der beiden Diodenspannungen Ud(t) nahezu identisch ist, sind die
Unterschiede in der Speicherladung ein anschauliches Maß für die unterschiedlichen
Schaltverluste. Die Unterschiede in der Speicherladung finden sich zudem zu einem
Zeitpunkt, in dem die Spannung an der Diode bereits verhältnismäßig hoch ist. Dadurch
gehen die unterschiedlichen Speicherladungen stark in einen Unterschied in den
Schaltverlusten ein.
Für die Einschaltverluste des IGBT gilt dies in ähnlicher Weise. Den Strom des IGBT beim
Einschalten erhält man, wenn man den gemessenen Diodenstrom aus Abbildung 18 um den
Laststrom nach oben verschiebt, so dass die Kurve bei 0A beginnt. Für die Spannung am
IGBT gilt
U CE (t ) + U d (t ) = U zk = const ,
(12)
sofern man induktive Spannungsabfälle vernachlässigt. Dies ist zulässig, da bei dem
gezeigten, relativ kleinen Strom induktive Spannungsabfälle nur eine untergeordnete Rolle
spielen.
Die Verluste des IGBT beim Einschalten können aus den gemessenen Kurven somit
berechnet werden zu
E onIGBT = ∫ (U zk − U d (t ) ) (I Last + I d (t ) ) dt
(13)
An dieser Gleichung ist zu erkennen, dass die unterschiedliche Speicherladung bei den
Einschaltverlusten des IGBT eine geringere Rolle spielt als bei den Ausschaltverlusten der
Diode. Zum einen bildet der Diodenrückstrom nur einen Teil des IGBT-Stromes, da im IGBT
noch der Laststrom fließt. Zum anderen wirkt nun der umgekehrte Effekt wie bei der
Auswirkung auf die Schaltverluste der Freilaufdiode: die Unterschiede in der Speicherladung
treten in einem Zeitbereich auf, in dem der IGBT seine Spannung bereits weitgehend
abgegeben hat. Aus diesem Umstand lässt sich die generelle Aussage ableiten, dass mit
zunehmender Schaltgeschwindigkeit die Verlustanteile während des Einschaltvorganges
eines IGBT zunehmend von der Diode übernommen werden.
2.2.2 Die SiC-Schottkydiode
Wie bereits beschrieben, führt die Speicherladung in bipolaren Bauelementen zu
Schaltverlusten. Deshalb muss für Anwendungen mit hoher Schaltfrequenz die
Speicherladung der verwendeten Halbleiterbauelemente reduziert werden. In der Praxis
haben sich für Anwendungen mit sehr hoher Schaltfrequenz, wie z.B. Schaltnetzteile,
29
deshalb unipolare Bauelemente wie MOSFETS oder Schottkydioden durchgesetzt [110], die
überhaupt keine Speicherladung besitzen.
Abbildung 19 zeigt die Struktur einer Schottkydiode:
A
Metall
n-
n+
K
Abbildung 19: Struktur der Schottkydiode
Auf der Anodenseite wird das p-Gebiet der pn-Diode durch eine Metallschicht ersetzt. Die
Sperrspannung des Leistungshalbleiters wird wiederum in einem schwach dotierten n-Gebiet aufgenommen, dessen Dicke von der erforderlichen Sperrspannung abhängt. Die
Grenzfläche zwischen dem Metall und der schwach dotierten Schicht des Halbleiters wird als
Metall-Halbleiter-Übergang oder Schottky-Kontakt bezeichnet. Die Durchlassspannung der
Schottkydiode ergibt sich aus der Summe des Spannungsabfalls am Metall-HalbleiterÜbergang und dem ohmschen Spannungsabfall über dem schwach dotierten Mittelgebiet,
sofern man ohmsche Kontaktwiderstände an Kathode und Anode vernachlässigt.
2.2.2.1 Der Schottky-Kontakt
Der Schottky-Kontakt bildet sich an der Grenzfläche zwischen einem Metall und einem
Halbleiter [100]. Zu seiner Beschreibung sei zunächst angenommen, Metall und
Halbleitermaterial seien separiert.
In Abbildung 20 sind die Energieniveaus von einem Metall und einem Halbleiter dargestellt.
Aufgrund der Materialstruktur können nur bestimmte definierte Energieniveaus von den
Elektronen eingenommen werden. Die Vielzahl nahe beieinander liegender möglicher
Energieniveaus wird als Energieband bezeichnet. Das Energieband, das von gebundenen
Elektronen der äußeren Schale, den Valenzelektronen, besetzt wird, wird als Valenzband
bezeichnet und ist in Abbildung 20 als graue Fläche dargestellt. Sobald ein Elektron zur
elektrischen Leitfähigkeit beitragen soll, muss es zusätzlich Energie aufnehmen und somit
ein höheres Energieniveau besetzen. Die Energieniveaus der Elektronen, die zusätzliche
Energie besitzen und die nahe beieinander liegen, werden als Leitungsband bezeichnet. Das
Leitungsband ist in Abbildung 20 farbig dargestellt.
30
Abbildung 20: Darstellung der Energieniveaus in Metall und Halbleiter
Im Metall existieren sehr viele frei bewegliche Elektronen, weil oberhalb des Fermi-Niveaus
beliebig viele freie Zustände anzutreffen sind, wodurch das Material leitfähig wird. Im
Halbleiter existiert dagegen zwischen dem obersten Niveau des Valenzbandes und dem
untersten Niveau des Leitungsbandes ein Bereich von Energie, in dem keine freien Zustände
existieren. Dieser Bereich wird als Bandlücke bezeichnet und ist eine wichtige Kenngröße
eines Halbleitermaterials.
Die Wahrscheinlichkeit, dass ein bestimmtes Energieniveau von einem Elektron besetzt wird,
wird durch die Fermiverteilung beschrieben [44]:
f (E) =
1
1+ e
(14)
E − EF
kT
Der Parameter EF bezeichnet das Energieniveau, bei dem die Wahrscheinlichkeit 0,5 beträgt
und wird als Fermi-Niveau bezeichnet. Bei hohen Energieniveaus nähert sich die
Fermiverteilung dem Wert null (die Aufenthaltswahrscheinlichkeit ist sehr gering), bei
niedriger Energie dem Wert eins. Der Abstand des Fermi-Niveaus vom Vakuumlevel wird als
Austrittsarbeit Φ bezeichnet.
Bei einem undotierten Halbleiter liegt das Fermi-Niveau in der Mitte der Bandlücke. Wird der
Halbleiter mit einem Element der 5. Gruppe dotiert (z.B. Phosphor), so werden zusätzliche
Elektronen eingebracht (n-Dotierung), die lokale Zustände nahe des Leitungsbandes haben.
Die Wahrscheinlichkeit, dass ein Elektron in das Leitungsband gelangen kann, nimmt zu, das
Fermi-Niveau nähert sich abhängig von der eingebrachten Dotierkonzentration dem
Leitungsband.
31
Energie
Vakuumlevel
EC
EFH
EV
Halbleiter
1
0,5
f(E)
Abbildung 21: Definition des Fermi-Niveaus, Beispiel n-dotierter Halbleiter
Bei der Betrachtung des Schottkykontaktes wird analog zu Abbildung 20 von einem ndotierten Halbleiter ausgegangen, dessen Fermi-Niveau über dem Fermi-Niveau des Metalls
liegt. Werden die beiden Festkörper kontaktiert, so fließen im Bereich der Grenzfläche
Elektronen von dem Halbleiter in das Metall, die Fermi-Niveaus von Metall und Halbleiter
gleichen sich einander an. Diese Elektronen hinterlassen in dem Halbleiter positiv geladene
Ionen, die somit eine Raumladungszone bilden. Die Menge der erforderlichen Raumladung
hängt hierbei von dem Unterschied zwischen den Austrittsarbeiten ΦM des Metalls und ΦH
des Halbleiters ab. Dieser Unterschied wird als Schottkybarriere Φb bezeichnet und ist
proportional zu der Differenz zwischen dem Fermi-Niveau des Metalls und der unteren
Leitungsbandkante des Halbleiters:
Φb =
EC − E FM
q
(15)
Das Potenzial im Festkörper wird durch die Poisson-Gleichung beschrieben. Diese lautet im
eindimensionalen Fall:
ρ
d 2Φ
=−
,
2
εr ε0
dx
(16)
wobei ρ die gesamte im betrachteten Gebiet eingeschlossene Ladung beschreibt. Die
eingeschlossene Ladung besteht aus der Ladung der ionisierten Donatoren und der freien
Elektronen und Löcher. In der Raumladungszonekönnen können die freien Ladungsträger
vernachlässigt werden, so dass unter der Annahme vollständiger Ionisation gilt:
32
ρ = q ND
(17)
x
A
x
p
Metall
x
O
E
+ +
+ +
+ +
n-
a) Struktur
b) Ladung
c) Feld
d) Potenzial
Abbildung 22: Feldverlauf und Potenzial an der Schottkybarriere
Der Verlauf des elektrischen Feldes kann mit
E = − gradΦ = ∫
q ND
ε ε0
(18)
dx
berechnet werden.
Im Metall ist eine sehr große Anzahl an Ladungsträgern vorhanden, die nach Gl. (18) zu
einem extrem hohen Feldgradienten führt. Im Metall ist aufgrund des hohen Gradienten
keine ausgedehnte Raumladungszone vorhanden, in erster Näherung kann das elektrische
Feld an dieser Stelle als Sprung auf null nachgebildet werden.
Wird an die Anschlüsse der Schottkydiode eine externe Spannung angelegt, bei der die
Anode ein negatives Potenzial gegenüber der Kathode annimmt, so wird der Abfluss der
Elektronen aus dem Halbleitermaterial in das Metall verstärkt. Die Raumladungszone weitet
sich auf, und die Diode nimmt Sperrspannung auf.
Wird durch eine externe Spannungsquelle das Potenzial der Anode gegenüber der Kathode
erhöht, so wird die Raumladungszone aus Abbildung 22 reduziert und das interne Potenzial
abgebaut. Übersteigt der Betrag der positiven externen Spannung an der Anode das interne
Potenzial des Schottkykontaktes, so können Elektronen von der Kathode über den MetallHalbleiter-Übergang zur Anode fließen; die Diode befindet sich im Durchlasszustand. Die
Überwindung des internen Potenzials ist an den externen Kontakten der Diode als
Schwellenspannung messbar. Die Höhe dieser Schwellenspannung hängt von dem internen
Potenzialverlauf und somit von Φb ab.
33
2.2.2.2 Die Driftzone
Die schwach dotierte Schicht des Halbleitermaterials wird als Driftzone bezeichnet. Sie ist
erforderlich, um die Sperrspannung der Schottkydiode aufzunehmen. Mit zunehmender
Sperrspannung wird das elektrische Feld am Metall-Halbleiter-Übergang zunehmen. Nach
Gl.(18) ist der Feldgradient durch die Dotierung bestimmt, die aufgenommene
Sperrspannung kann über das Integral über das elektrische Feld bestimmt werden.
Die maximale Sperrspannung, die eine Schottkydiode aufnehmen kann, wird durch die
maximale Feldstärke begrenzt, die im Halbleiter auftreten darf und durch die Höhe der
Schottky-Barriere, die den Sperrstrom bestimmt. Oberhalb dieser maximalen Feldstärke
können in den Atomen der Raumladungszone freie Elektronen und Löcher durch Aufbrechen
der Atombindungen erzeugt werden. Der Sperrstrom steigt in diesem Fall lawinenartig an
und durch die gleichzeitig anliegende hohe Spannung wird in der Diode sehr hohe
Verlustleistung umgesetzt, die zu einer Beschädigung der Diode führt. Aus diesem Grund
darf de maximal zulässige elektrische Feldstärke in der Diode nicht überschritten werden.
E
Ekrit2
Ekrit1
x
w2
w1
Abbildung 23: Verlauf des elektrischen Feldes bei Materialien mit unterschiedlicher kritischer
Feldstärke
Die Höhe der maximal zulässigen kritischen Feldstärke ist für die Auslegung einer Diode von
großer Bedeutung. In Abbildung 23 ist der Verlauf des elektrischen Feldes für zwei
Bauelemente dargestellt, deren kritische Feldstärke sich um den Faktor 2 unterscheidet. An
beiden Bauelementen liegt die gleiche Sperrspannung an, die durch die Fläche unter der
Kurve des elektrischen Feldes festgelegt ist. Die Diode mit der höheren kritischen Feldstärke
benötigt eine proportional geringere Dicke w. Darüber hinaus sind der Feldstärkegradient
und damit die Dotierung der schwach dotierten Mittelschicht proportional höher. Unter der
Annahme vollständiger Ionisation berechnet sich der Driftwiderstand der Diode zu [109]:
R Drift =
mit:
w
q µn N D A
w:
q:
µn:
ND:
A:
(19)
Dicke der Diode
Elementarladung
Beweglichkeit der Elektronen
Dotierungskonzentration in der schwach dotierten Mittelschicht
Fläche der Diode
34
Die zulässige Dotierungskonzentration wird als kritische Ladung bezeichnet und ergibt sich
aus der Poisson-Gleichung zu
q ND = ε
E krit
w
(20)
Die maximale Sperrspannung, die die Diode aufnehmen kann, beträgt
U s max =
1
w E krit
2
(21)
Durch Einsetzen von Gl. (20) und Gl. (21) in Gl. (19) ergibt sich der Driftzonenwiderstand in
Abhängigkeit der kritischen Feldstärke zu:
RD =
4 U s max
2
(22)
µn ε E krit A
3
Der Driftzonenwiderstand reduziert sich somit mit der dritten Potenz des kritischen
elektrischen Feldes des Halbleitermaterials. Für den Vergleich zwischen Silizium und
Siliziumkarbid überwiegt dieser Einfluss deutlich gegenüber den Unterschieden in µn und ε.
Das kritische elektrische Feld in Silizium beträgt 24V/µm. Für Siliziumkarbid liegt diese
kritische elektrische Feldstärke etwa bei 200 - 300V/µm ([5],[117]). Deshalb können
Schottkydioden in Siliziumkarbid bei einer gegebenen Sperrspannung mit wesentlich
geringerem spezifischem Durchlasswiderstand realisiert werden. Für eine erforderliche
Sperrspannung von 1700V kann eine Diode mit einem spezifischen Driftwiderstand von
2mΩcm2 bei einer Temperatur von 25°C erreicht werden. In Silizium wäre dieser Wert
rechnerisch um den Faktor 1000 höher. In der Praxis sind Silizium-Schottkydioden wegen
des hohen Driftzonenwidestandes nur bis zu einer Sperrspannung von ca. 200V verfügbar,
für höhere Sperrspannung müssen pn-Dioden eingesetzt werden, deren schwach dotiertes
Mittelgebiet im Durchlasszustand von Ladungsträgern überschwemmt wird. Für hohe
Schaltfrequenz bietet eine Schottkydiode jedoch einen immensen Vorteil durch die fehlende
Speicherladung und dadurch bedingt die wesentlich geringeren Schaltverluste.
2.2.2.3 Parallelschaltbarkeit von SiC-Schottkydioden
Da bei Bauelementen aus SiC die Dichte von Defekten auf dem Wafer im Vergleich zu
Silizium sehr hoch ist, können mit wirtschaftlicher Ausbeute nur verhältnismäßig kleine Chips
hergestellt werden. Um dennoch Stromrichter mit der geforderten Ausgangsleistung bis
55kW herstellen zu können, müssen diese Chips parallel geschaltet werden.
35
A
ILast
Uth1
Uth2
Rdrift1
Rdrift2
Rsub1
Rsub2
K
Abbildung 24: Parallelschaltung zweier Schottkydiodenchips
In Abbildung 24 ist ein Modell für die Parallelschaltung von zwei Chips dargestellt, es ist auf
beliebig viele Chips erweiterbar. In der Parallelschaltung wird die Summe der
Schleusenspannung und des Spannungsabfalls am Driftwiderstand und des
Substratwiderstandes für alle Chips identisch sein. Die Aufteilung des Laststromes auf die
einzelnen Chips wird von den einzelnen Impedanzen bzw. von den Toleranzen der
Impedanzen zwischen den einzelnen Chips abhängen. Hierbei ist zwischen zwei Effekten zu
unterscheiden:
a) Aufgrund von Fertigungstoleranzen können einzelne Parameter unterschiedliche
Werte aufweisen.
b) Aufgrund dieser Toleranzen können die Chips unterschiedliche Temperaturen
annehmen. Diese unterschiedlichen Temperaturen können wiederum zu weiteren
Parameterunterschieden führen. Diese temperaturbedingten Parameterunterschiede
können auch bei Parametern auftreten, die keine fertigungsbedingten Abweichungen
besitzen.
Die Schleusenpannung eines SiC-Schottkydiodenchips wird im Wesentlichen durch die
Eigenschaften des Schottkykontaktes bestimmt. Bei gegebener Temperatur sind
Unterschiede in der Schleusenspannung zwischen einzelnen Chips vernachlässigbar.
Allerdings ändert sich die Schleusenspannung mit der Temperatur. Für die Höhe der
Schwellenspannung gilt [9]:
U S = Φb +
⎞
k T ⎛⎜ I Last
ln ** 2 ⎟
q ⎜⎝ A T A ⎟⎠
(23)
A** bezeichnet hierbei die effektive Richardson-Konstante. Im praxisrelevanten
Arbeitsbereich mit einer Stromdichte bis 300A/cm2 und einem Temperaturbereich zwischen
270K und 500K ist der Logarithmusterm immer negativ. Mit steigender Temperatur nehmen
sowohl der Logarithmusterm als auch sein Vorfaktor betragsmäßig zu, so dass die Höhe der
36
Schwellenspannung mit der Temperatur abnimmt. Bei der Betrachtung eines
Temperaturbereiches zwischen 273K und 423K ergibt sich jedoch nur eine Änderung dieser
Schwellenspannung unter 0.1V, so dass dieser Effekt nur einen sehr geringen Einfluss
besitzt.
Die Berechnungsformel für den Driftwiderstand ist in Gl. (19) gegeben. Fertigungsbedingte
Toleranzen des Driftwiderstandes treten in erster Linie bei der Dicke w der Driftzone und
deren Dotierung ND auf. Diese Unterschiede können durch die Messung der statischen
Durchlasseigenschaften der Diodenchips eines Wafers ermittelt werden.
Abbildung 25: Kumulative Häufigkeit des Gesamtwiderstandes (Summe aus Driftzonenwiderstand und Substratwiderstand) für Dioden aus 3 SiC-Wafern bei T=300K (Quelle: Fa. SiCED)
In Abbildung 25 ist zu erkennen, dass innerhalb eines Wafers der Durchlasswiderstand der
Schottkydioden um maximal 25mΩ voneinander abweicht. Bezieht man alle Wafer in die
Betrachtung mit ein, so beträgt die maximale Abweichung 43mΩ.
Die temperaturabhängige Größe in Gl. (19) ist die Beweglichkeit der Elektronen µn. Die
Temperaturabhängigkeit der Beweglichkeit ist aus Messungen bekannt [61]:
⎛ T ⎞
μ n (T ) = μ n (300 K ) ⎜
⎟
⎝ 300 ⎠
βn
(24)
Der Exponentialterm βn ist von der Dotierung der Epitaxieschicht abhängig, auch diese
Abhängigkeit ist messtechnisch bekannt. Bei der betrachteten Dotierungskonzentration von
4*1015/cm3 beträgt der Exponentialterm βn = -2,6.
Der zweite Widerstand Rsub aus Abbildung 24 bezeichnet alle weiteren ohmschen
Widerstände in der Schottkydiode. Dies sind vornehmlich der Substratwiderstand des SiCGrundmaterials und ohmsche Kontaktwiderstände. Da diese Widerstände bei 1700VBauteilen deutlich kleiner als der Driftwiderstand sind, ist es in erster Näherung zulässig,
deren Parameterstreuungen und Temperaturabhängigkeiten zu vernachlässigen.
37
Mit diesen Werten kann unter Verwendung der thermischen Ersatzwiderstände der SiCDiodenchips eine Berechnung der Stromverteilung auf die einzelnen Chips durchgeführt
werden. Neben der statischen Abweichung aufgrund der Parameterstreuungen ist vor allem
die temperaturbedingte Abweichung aufgrund der temperaturabhängigen Beweglichkeit µn(T)
von Interesse. Trägt man die Durchlasskennlinie eines Chips bei verschiedenen
Temperaturen
auf,
so
ist
zu
erkennen,
dass
für
alle
praxisrelevanten
Umrichterausgangsströme die Durchlassspannung der Diode einen positiven
Temperaturkoeffizienten besitzt. Dies ist auch aus dem Datenblatt eines Moduls mit SiCSchottkydioden ersichtlich.
Abbildung 26: Durchlasskennlinie der 42A SiC-Diode [56]
Ein Diodenchip einer Parallelschaltung, der aufgrund von Parametertoleranzen einen
geringeren Driftwiderstand besitzt und somit einen erhöhten Laststrom führt, wird stärker
erwärmt als die benachbarten Diodenchips der Parallelschaltung, weil die Spannung in der
Parallelschaltung für alle Dioden identisch ist. Der positive Temperaturkoeffizient führt dazu,
dass der Driftwiderstand des einen Diodenchips zunehmen wird und somit dem erhöhten
Laststrom entgegenwirkt. Deshalb ist eine überproportionale Konzentration des Laststroms
auf eine einzige Diode nicht zu befürchten.
Die Kennlinie der Diode für eine Sperrschichttemperatur von 120°C zeigt einen
charakteristischen Knick bei einer Durchlassspannung von ca. 3,3V. Dieser ist dadurch zu
erklären, dass der Randabschluss der Diode mit einem implantierten pp+-Ring ausgeführt ist.
Diese Technologie ist in der Literatur als junction termination edge (JTE) bekannt. Bei sehr
hoher Stromdichte kann dieser p+-Ring Ladungsträger in die Diode injizieren, da er als der
Schottkydiode parallel geschaltete pn-Diode wirkt, deren Schleusenspannung in SiC etwa
2,8V beträgt. Dieses Verhalten verbessert die Robustheit der Schottkydiode bei Belastung
mit hohem Stoßstrom, ist sonst jedoch für das elektrische Verhalten irrelevant, da derart
hohe Stromdichten in der Praxis nicht erreicht werden.
Der beschriebene positive Temperaturkoeffizient der Schottkydiode stellt zwar sicher, dass
keine Stromkonzentration auf eine Diode in der Parallelschaltung auftritt, dennoch ist für die
Dimensionierung eines Umrichters eine quantitative Aussage erforderlich, mit wie viel
Fehlverteilung des Laststrom bei einer bestimmten Anzahl parallel geschalteter Dioden zu
38
rechnen ist. Dies kann mit Hilfe einer iterativen thermoelektrischen Berechnung ermittelt
werden.
Für die thermische Nachbildung der Parallelschaltung wird eine einfache Ersatzanordnung
verwendet. Bei dieser befinden sich alle Diodenchips auf einer thermisch unendlich gut
leitfähigen Oberfläche, die eine vorgegebene Temperatur besitzt und somit die Oberfläche
einer Modulbodenplatte nachbildet. Die Temperatur dieser Oberfläche ist konstant und somit
unabhängig von den Verlusten der Diodenchips. Die Temperatur der Diodenchips ergibt sich
durch den thermischen Widerstand der Chips zu dieser Bodenplatte und die in der Diode
anfallenden Verluste, die von der Stromaufteilung in der Parallelschaltung abhängen.
Als Startbedingung für die Iteration wird eine worst case Bedingung gewählt, die sich aus
den Bauelementdaten aus Abbildung 25 ergibt. Es wird dabei angenommen, dass bei einer
Parallelschaltung von n Chips ein Chip einen minimalen Widerstand und die anderen n-1
Chips den maximalen Widerstand aufweisen. Die Schleusenspannungen der Chips werden
als gleich angenommen
Mit diesen Startbedingungen werden die Stromaufteilung, die Verlustleistung und die daraus
resultierende neue Chiptemperatur berechnet. Anschließend wird für die nächste
Iterationsschleife aus dieser Chiptemperatur der neue Widerstand mit Hilfe von Gl. (19) und
Gl. (24) sowie die neue Schleusenspannung mit Gl. (23) berechnet. Für weitere
Iterationsschleifen ist die Vorgehensweise identisch. Die Iteration wird abgebrochen, sobald
die Temperaturänderung der Chips im Vergleich zum letzten Iterationsschritt einen
vorgegebenen Wert unterschreitet.
Um eine Abschätzung zu erhalten, inwiefern der Temperaturkoeffizient auf die
Stromverteilung überhaupt einen Einfluss hat, wurde die Stromverteilung in Abhängigkeit der
Parallelschaltzahl berechnet:
Stromkonzentration im heißesten Chips
Strom im heißesten Chip/ Strom bei
identischen Chips
1.11
Vernachlässigung des positiven Temperaturkoeffizienten
1.1
1.09
Berücksichtigung des positiven
Temperaturkoeffizienten
1.08
1.07
1.06
1.05
1.04
2
3
4
5
6
7
8
9
10
Anzahl parallelgeschalteter Diodenchips
Abbildung 27: Einfluss des positiven Temperaturkoeffizienten
Vernachlässigt man die Temperaturabhängigkeit der Schottkydiode, so wird die
Stromaufteilung unmittelbar von der Differenz der Durchlasswiderstände aufgrund von
39
Parameterstreuungen bestimmt. Mit den Bauelementdaten aus Abbildung 25 ergibt sich
damit die schwarze Kurve in Abbildung 27. Diese kann analytisch berechnet werden:
I Last
I1
I mittel
=
R2
n −1
R
n
R2
R1 + 2
n −1
n −1 =
R
I last
R1 + 2
n −1
n
(25)
mit:
I1:
Imittel:
ILast:
R1:
R2:
n:
Strom durch den Chip mit geringerem Widerstand
Strom durch einen Chip bei identischen Widerständen
Gesamtstrom, der durch die Parallelschaltung fließt
Widerstandswert des einen Chips mit minimalem Ron
Widerstandswert eines Chips mit maximalem Ron
Anzahl der parallel geschalteten Chips
Für eine sehr hohe Anzahl parallel geschalteter Chips nähert sich der Grenzwert von Gl. (25)
für n→∞ dem Wert R2/R1 an. Rechnet man dies mit den Werten aus Abbildung 25 für einen
Wafer umgerechnet auf 80°C, so ergibt sich ein Grenzwert von ca. 1,12.
In der magentafarbenen Kurve aus Abbildung 27 kann der Einfluss des positiven
Temperaturkoeffizienten abgelesen werden. Die Stromfehlverteilung wird bei den für den
Demonstratorumrichter verwendeten Chipdaten um ca. 10% reduziert. Für die praktische
Anwendung bedeutet dies, dass trotz des verhältnismäßig starken positiven
Temperaturkoeffizienten aus Gl. (24) noch 90% der parameterbedingten Fehlverteilung
bestehen bleiben. Diese darf somit bei der Auslegung der Parallelschaltung nicht mit dem
Argument eines positiven Temperaturkoeffizienten vernachlässigt werden.
Die aufgrund der parameterbedingten Streuungen auftretende Temperaturüberhöhung am
heißesten Chip ist unter Berücksichtigung der temperaturabhängigen Bauelementgrößen in
Abbildung 28 dargestellt:
Temperaturüberhöhung des heißesten Chips
Temperatur heißester Chip/ Temperatur bei
identischen Chips
1.2
Chips aus verschiedenen Wafern
1.18
1.16
1.14
1.12
1.1
1.08
Chips aus einem Wafer
1.06
1.04
1.02
1
2
3
4
5
6
7
8
Anzahl parallelgeschalteter Diodenchips
Abbildung 28: Temperaturüberhöhung des heißesten Chips
40
9
10
Auch bei dieser Berechnung wurden die Daten aus Abbildung 25 verwendet. Durch die
Verwendung von Chips aus nur einem Wafer kann die Temperaturüberhöhung halbiert
werden, weil auch die Ränder der Verteilung um den Faktor 2 reduziert werden. Diese
Temperaturüberhöhung ist die relevante Größe bei der Auslegung der Parallelschaltung.
Soll die Temperaturüberhöhung weiter abgesenkt werden, so ist dies über eine geschickte
Selektion der Chips eines Wafers für eine Parallelschaltung möglich. Hierbei kann die
Tatsache ausgenutzt werden, dass die Schwankung des Driftwiderstandes bei Chips auf
einem Wafer technologisch bedingt und somit systematisch ist. Die wesentliche Ursache für
die Schwankung sind Unterschiede in der Dotierung des Driftgebietes, die während der
Epitaxie entstehen. Diese Dotierung ist in der Wafermitte maximal und sinkt zum Rand in
erster Näherung rotationssymmetrisch ab. Werden die Chips beim Einbau in ein
Halbleitermodul gemäß einer Spirale von außen nach innen oder umgekehrt entnommen, so
kann die Temperaturüberhöhung innerhalb einer Parallelschaltung minimiert werden. Für
dieses optimierte Verfahren wurde ein Patent angemeldet [57].
Ron
Start
Linker
Waferrand
Wafermitte
Rechter
Waferrand
Entnahmereihenfolge der Chips
Abbildung 29: Vorteilhafte Chipentnahme zur Reduzierung der Stromfehlverteilung in der
Parallelschaltung
2.2.2.4 Bestimmung der Chipgröße der SiC-Dioden
Mit den Halbleiterbauelementen sollen Umrichter im mittleren Leistungsbereich realisiert
werden. Hierfür wird ein Bereich von 15kW bis 55kW ausgewählt, was einem
Umrichterausgangsstrom von 19A bis 62A entspricht. Bei Standardumrichtern mit
Siliziumbauelementen können derartige Ausgangsströme ohne Parallelschaltung von Chips
realisiert werden, die genannten Einschränkungen, die durch Parallelschaltung entstehen,
sind somit nicht relevant.
Neben den positiven Eigenschaften des Halbleitermaterials Siliziumkarbid besteht ein
wichtiger Nachteil darin, dass die Anzahl der Defektstellen auf einem Wafer deutlich größer
ist als bei einem Siliziumwafer ([103], [133]). Da eine Defektstelle den betroffenen Chip
unbrauchbar macht, führen diese Defektstellen zu einer Reduzierung der Ausbeute und
somit zu einer Steigerung der Kosten. Aufgrund der Anzahl der Defektstellen wird die
Ausbeute durch die Größe der Halbleiterchips bestimmt, da bei großen Chips durch eine
Defektstelle eine größere Halbleiterfläche verworfen werden muss. Bei zufällig verteilten
Defektstellen mit der Defektdichte D auf dem Wafer gilt für die Ausbeute für Chips mit der
Fläche AChip:
41
Ausbeute = e
(26)
− D AChip
Bei gegebener Defektdichte nimmt die Ausbeute mit größer werdender Chipfläche ab. Dies
würde nahe legen, dass die Chipfläche möglichst klein gewählt werden muss, um die
Ausbeute zu maximieren. Allerdings ist das entscheidende Kriterium für die bestmögliche
Ausnutzung des Wafers nicht allein die Chipausbeute, sondern die Fläche des Wafers, die
zur aktiven Stromführung genutzt werden kann. Der Chiprand mit der Breite bRand ist für die
aktive Stromführung nicht nutzbar. Er besteht aus einem ersten Bereich, der für den Abbau
des elektrischen Feldes von der Anode auf der Chipoberfläche bis zur Sägekante, die auf
Kathodenpotenzial liegt, genutzt wird. Der zweite Bereich des Chiprandes ist für den
mechanischen Sägevorgang erforderlich, der den Wafer in einzelne Chips zerteilt. Für eine
gegebene Chipfläche und eine gegebene erforderliche Randbreite wird die
Flächenausnutzung des Chips maximal, wenn der Chip als Quadrat ausgeführt wird. In
diesem Fall gilt:
Ausnutzung Chip =
Aaktiv ,Chip
AChip
(
=
AChip − 2 b Rand
)
2
(27)
AChip
Bei gegebener Randbreite wird die aktive Fläche für möglichst große Chips maximal. Die
gesamte aktive Waferfläche ergibt sich durch Multiplikation von Gl. (26) und Gl. (27) bei
Vernachlässigung der Unstetigkeiten am Waferrand:
Ausnutzung Wafer =
Aaktiv ,Wafer
AWafer
= Ausnutzung Chip ⋅ Ausbeute
(28)
Zur Veranschaulichung sind die einzelnen Größen schematisch dargestellt:
AChip
bRand
Aaktiv,Chip
Aaktiv,Wafer
Defektstelle
Abbildung 30: Definition von Randbreite, Chipfläche, aktiver Chipfläche und aktiver
Waferfläche
42
Für eine Defektdichte von 5 Defekten/cm² und einer Randbreite von 100µm sind die
Flächenausnutzung eines guten Chips, die Ausbeute und die Flächenausnutzung des
Wafers als Funktion der Chipgröße dargestellt:
100
AusnutzungChip
90
80
70
[%]
60
AusnutzungWafer
50
Ausbeute
40
30
20
10
0
0
2
4
6
8
10
12
14
16
18
20
2
Chipfläche/[mm ]
Abbildung 31: Ausnutzung der Waferfläche, berechnet aus Ausbeute und Ausnutzung der
Chipfläche
Die aktiv nutzbare Waferfläche als Funktion der Chipgröße zeigt ein charakteristisches
Maximum, im vorliegenden Fall liegt dies bei einer Chipgröße von ca. 3mm2. Da dieses
Maximum für die tatsächliche Gestaltung des Chips von großer Bedeutung ist, wird es für
verschiedene Randbreiten und Defektdichten dargestellt:
Optimale Diodenfläche
20
18
16
14
18-20
12
10
8
6
450
250
50
0
1
2
3
4
5
6
7
8
9
10
16-18
14-16
12-14
10-12
8-10
4
6-8
2
4-6
0
Randbreite
brand/
[µm]
Optimale
Chipfläche/[mm2]
2-4
0-2
Defektdichte D/[cm-2]
Abbildung 32: Optimale Chipfläche in Abhängigkeit von Randbreite und Defektdichte
43
Mit einer sinkenden Anzahl von Defektstellen kann die Chipfläche vergrößert werden. Mit
zunehmender Randbreite nimmt die optimale Chipgröße ebenfalls zu, wobei in diesem Fall
die aktiv nutzbare Waferfläche sinkt:
Maximal mögliche Waferausnutzung
1
0.9
0.8
0.7
0.9-1
0.6
0.5 AusnutzungWafer
0.4
Randbreite
brand/[µm]
250
450
10
9
8
7
6
5
4
3
2
0.6-0.7
0.5-0.6
0.4-0.5
0.2
0.3-0.4
0
50
0.7-0.8
0.3
0.1
1
0.8-0.9
0.2-0.3
0.1-0.2
0-0.1
0
Defektdichte D/[cm-2]
Abbildung 33: Maximal mögliche Waferausnutzung in Abhängigkeit von Randbreite und
Defektdichte
Für eine optimale Ausnutzung des Wafers wird angestrebt, sowohl die Defektdichte als auch
die Randbreite möglichst gering zu halten.
Die Maximierung der aktiv nutzbaren Waferfläche stellt das wichtigste Optimierungsziel für
ein kostenoptimiertes Halbleitermodul dar. Allerdings spielen bei dieser Optimierung für eine
geeignete Ausführung des Halbleitermoduls noch andere Punkte eine Rolle, die an dieser
Stelle erwähnt werden sollen:
¾ Die Verwendung von vielen kleinen Chips verbessert den Freiheitsgrad, in einem
Halbleitermodul, die Chips auf eine größere Fläche zu verteilen. Dies spart zwar
keine Verlustleistung, die für die Auslegung des Kühlsystems des Umrichters
maßgebend ist, aber die Halbleiterfläche kann besser ausgenutzt werden, weil
der Temperaturhub reduziert wird. Dieser Vorteil kann nur am Einzelfall eines
Halbleitermoduls quantitativ bewertet werden, da er von dem Füllgrad des Moduls
mit Chips und dem Layout der DCB abhängt.
¾ Eine hohe Parallelschaltzahl führt zu einem Derating aufgrund nicht idealer
Stromverteilung (s. Kap. 2.2.2.3)
¾ Eine minimale Chipfläche ist erforderlich, um den Chip mittels eines Bonddrahtes
zu kontaktieren.
¾ Kleine Chips erhöhen einzelne Fertigungsschritte, z.B. Sägen des Wafers, Testen
und Bonden der Chips. Diese Themen sind im Einzelfall von der
Fertigungstechnologie abhängig und können nur für konkrete Beispiele
quantifiziert werden.
44
2.2.2.5 Dynamisches Abschaltverhalten der SiC-Schottkydiode
Der wesentliche Vorteil der Schottkydiode zeigt sich in ihrem dynamischen Abschaltverhalten
[16]. Da in der Schottkydiode keine Speicherladung existiert, müssen beim Abschaltvorgang
auch keine Minoritätsladungsträger ausgeräumt werden.
IGBT-Einschalten der Testmodule, 35A, 125°C
2400
200
Si
2100
150
1800
100
1500
50
SiC
1200
0
900
-50
600
-100
300
-150
0
0.00
Ic/[A]
Uce/[V
SiFast
-200
200.00
400.00
600.00
800.00
1000.00
t/[ns]
Abbildung 34: Kommutierungsvorgang von Si-Dioden und der SiC-Schottkydiode
In Abbildung 34 sind die Zeitverläufe von Strom (oben) und Spannung (unten) an einem
IGBT während des Kommutierungsvorgangs beim Einsatz unterschiedlicher Freilaufdioden
dargestellt. Die roten und blauen Kurven zeigen den Kommutierungsvorgang der 1700VStandarddiode aus dem Halbleitermodul FS50R17KE3 [54] (Si) und einem für schnelles
Schalten optimierten 1700V-Diodenmuster (SiFast), deren Strom- und Spannungsverläufe
an der Diode bereits in Abbildung 18 dargestellt wurden.
Der Kommutierungsvorgang der SiC-Schottkydiode (grüne Kurven) zeigt das erwartete
Verhalten der fehlenden Speicherladung. Für den einschaltenden IGBT ergeben sich
dadurch folgende Vorteile, die zu reduzierten Schaltverlusten führen:
1) Durch die fehlende Speicherladung wird der Strom im einschaltenden IGBT reduziert,
der durch den Halbleiter fließt, solange noch hohe Spannung am IGBT anliegt.
2) Der Zeitbereich vom Nulldurchgang bis zur Rückstromspitze verschwindet bei der
Schottkydiode vollständig. In diesem Zeitbereich ist eine pn-Diode nur zu einem sehr
geringen Maß in der Lage, Spannung aufzunehmen, so dass beim
Kommutierungsvorgang mit einer pn-Diode in diesem Zeitbereich hohe Verluste im
einschaltenden IGBT anfallen.
3) Die zulässige Schaltgeschwindigkeit des Kommutierungsvorgangs wird – vor allem
bei pn-Dioden mit hoher Sperrfähigkeit – zum großen Teil von dem Abrissverhalten
der pn-Diode bestimmt. Der Abriss äußert sich in einer hohen Stromsteilheit des
Diodenstromes in dem Zeitbereich nach der Rückstromspitze, die in Verbindung mit
unvermeidlichen Streuinduktivitäten des Kommutierungskreises zu einer hohen
kurzzeitigen Spannungsbelastung der Diode führt. Die Schaltgeschwindigkeit muss
so begrenzt werden, dass im ungünstigsten Betriebspunkt – den üblicherweise eine
hohe Zwischenkreisspannung, ein niedriger Laststrom und eine niedrige Temperatur
darstellen – weder die maximale Sperrfähigkeit der Diode überschritten wird noch die
Diode durch dynamischen Avalanche zerstört wird. Da bei der Schottkydiode keine
Speicherladung ausgeräumt werden muss, entfallen diese Dimensionierungskriterien.
Die Schaltgeschwindigkeit wird deshalb nicht mehr durch die Eigenschaften der
45
Leistungshalbleiter
begrenzt,
sondern
durch
Systemanforderungen
wie
beispielsweise die maximal zulässige Spannungssteilheit an potenzialtrennenden
Bauelementen wie Optokopplern.
An der Schottkydiode selbst sind in den Kurvenverläufen nach Abbildung 34 überhaupt keine
Abschaltverluste erkennbar. Allerdings ist anhand der Kurvenverläufe schwer abschätzbar,
ob tatsächlich überhaupt keine Schaltverluste auftreten. Da die Fläche der SiC-Diode aus
Kostengründen möglichst klein sein soll, könnten bei hoher Schaltfrequenz auch geringe
Schaltverluste zu nennenswerter Temperaturerhöhung führen.
Deshalb sollen die Verluste der Schottkydiode kaloriemetrisch erfasst werden. Hierzu wurde
ein Zwei-Quadrantensteller (2QS) mit Spannungsumkehr verwendet. Dieser wurde mit zwei
Halbleitermodulen aufgebaut, wobei in Halbleitermodul 1 nur eine SiC-Schottkydiode
verwendet wird und in Halbleitermodul 2 die übrigen erforderlichen Bauteile. Beide
Halbleitermodule wurden auf unterschiedliche Kühlkörper montiert.
Modul und
Kühlkörper 1
Modul und
Kühlkörper 2
T1
D2
T2
D1
DUT
ILast
LLast
RLast
CZK
UZK
ULast
Abbildung 35: 2QS zur Ermittlung der Schaltverluste der SiC-Schottkydiode
Mit dem 2QS wird in der Last ein Gleichstrom aufgebaut. Hierbei existieren folgende
Schaltzustände:
I. T1 und T2 sind eingeschaltet: In diesem Fall fließt ein Strom durch T1, die Last, T2
und den Zwischenkreiskondensator. Die Spannung an der Last ist gleich der
Zwischenkreisspannung, der Strom in der Last steigt an.
II. T1 ist eingeschaltet, T2 ist abgeschaltet: Der Strom fließt über T1, die Last und D2.
Die Spannung an der Last ist sehr klein und gleich der Durchlassspannung von T1
und D2. Der Strom in der Last wird durch den Spannungsabfall an den Halbleitern
und dem ohmschen Anteil der Last geringfügig abgebaut.
III. T1 und T2 sind abgeschaltet: An der Last liegt die negative Zwischenkreisspannung
an. Der Strom fließt über die beiden Dioden. Er wird in der Last abgebaut.
IV. T2 ist eingeschaltet, T1 ist ausgeschaltet: Der Strom fließt über T2 und D1, das
Verhalten in der Last ist identisch zu Schaltzustand II.
46
ULast
ILast
UZK
Imittel
0
t
-UZK
Schaltzustand
IV
I
II
III
IV
Abbildung 36: Verlauf von Strom und Spannung in der Last
Die Spannungs-Zeit-Fläche an dem ideal induktiven Teil der Last muss im
eingeschwungenen Zustand null sein. Im Schaltzustand I muss deshalb positive SpannungsZeit-Fläche aufgebaut werden, die in den Schaltzuständen II, III und IV kompensiert wird.
Der Mittelwert des Stromes stellt sich dementsprechend ein. Je kürzer die Schaltzustände I
und III im Vergleich zu II und IV gewählt werden, desto geringer ist der Stromripple.
Werden die Schaltzustände im gleichen Maßstab verkürzt oder verlängert, so bleibt der
Mittelwert des Laststromes erhalten, während sich die Schaltfrequenz der Leistungshalbleiter
ändert. In der betrachteten Schottkydiode bleiben somit die Durchlassverluste identisch,
während eventuell vorhandene Schaltverluste mit der Schaltfrequenz ansteigen.
Um die Fehler in der Messung zu minimieren, ist es zweckmäßig, nicht direkt über
proportionale Veränderungen der Schaltzustände die Schaltfrequenz zu verändern. In
diesem Fall würde der Ripplestrom mit kleinerer Schaltfrequenz steigen, weil die Leitdauern
der Zustände I und III ansteigen. Die betrachtete Diode D1 führt jedoch nur in den
Schaltzuständen III und IV Strom, beim Übergang von IV nach I wird sie abkommutiert. Die
wesentlichen Durchlassverluste entstehen somit im Intervall IV. Deshalb werden die
Ansteuerpulse der Transistoren so eingestellt, dass der effektive Strom in D1 und somit der
effektive Strom im Intervall IV möglichst identisch bleiben. Insbesondere soll der Strom beim
Übergang von IV nach I immer identisch sein, damit das Schalten der Diode bei definierten
Bedingungen stattfindet. Durch Messen des Stromes in D1 können die Ansteuerpulse
dementsprechend adaptiert werden. Wichtige Randbedingung ist, dass die bezogene
Leitdauer von D1 immer konstant bleibt.
Mit diesen Randbedingungen wurde die Temperatur des Kühlkörpers unter dem Modul von
D1 nach der Anordnung in Abbildung 49 bei unterschiedlichen Schaltfrequenzen erfasst:
47
Temperaturerhöhung SiC-Schottkydiode
8
Temperaturerhöhung/[°C]
7
6
5
4
3
2
1
0
0
5
10
15
20
25
30
35
40
45
50
Schaltfrequenz/[kHz]
Abbildung 37: Temperaturerhöhung der Schottkydiode bei unterschiedlicher Schaltfrequenz
Die Messung wurde bei einem Diodenstrom von 5A durchgeführt. Im Vergleich zum
Diodennennstrom von 42A ist dies ein relativ kleiner Wert. Er wurde gering gewählt, um die
Temperaturerhöhung aufgrund der anfallenden Schaltverluste möglichst wenig mit
Durchlassverlusten zu überlagern.
Die gemessenen Temperaturerhöhungen sind durchweg sehr gering. Bei dem Kühlkörper
wurde darauf geachtet, den thermischen Widerstand groß zu halten, d.h. nur natürliche
Konvektion und ein Kühlkörper ohne Kühlrippen wurden verwendet. Als Messungenauigkeit
wirkt insbesondere eine Veränderung der Luftströmungsverhältnisse, z.B. durch Öffnen von
Fenstern etc. Deshalb wurde die Messeinrichtung abgedeckt. Alle diese Maßnahmen
besitzen jedoch den Nachteil, dass die Messzeit bis zum Erreichen eines stabilen Zustandes
verlängert wird. Bei der vorliegenden Messung war eine Messzeit von 3 Stunden für einen
Messpunkt erforderlich.
In Abbildung 37 ist deutlich zu erkennen, dass die Temperatur der Diode mit steigender
Schaltfrequenz zunimmt. Im Rahmen der Messgenauigkeit bildet die Kurve der
Temperaturerhöhung eine Gerade, wobei die Steigung die der Schaltfrequenz proportionalen
Verluste widerspiegelt, während der Offset die Durchlassverluste repräsentiert. Bei einer
Schaltfrequenz von 16kHz tritt auf dem gegebenen Kühlkörper eine Temperaturerhöhung
aufgrund der Schaltfrequenz von ca. 1,5°C auf, was der Hälfte der Durchlassverluste bei 5A
entspricht. Diese Temperaturerhöhung ist nicht besonders groß, soll jedoch bei der
Auslegung mit berücksichtigt werden.
Die Ursache für diese dynamischen Verluste liegt in der Tatsache, dass auch bei einer
Schottkydiode beim Abschalten eine Ladung ausgeräumt werden muss. Hierbei handelt es
sich um die freien Elektronen der Dotierungsatome in der schwach dotierten Zone, in der die
Raumladungszone aufgebaut wird. Dieses Phänomen ist in der Literatur ([110], [111])
beschrieben. Für Dioden mit vergleichbarer Performance in Durchlassrichtung ist diese
Ladung bei SiC-Bauelementen im Vergleich zu Si-Bauelementen aufgrund der stark
reduzierten Dicke deutlich reduziert.
48
2.2.2.6 Einschaltverhalten der SiC-Schottkydiode
Neben den Abschaltverlusten stellen auch die Einschaltverluste eine mögliche
Verlustleistungsquelle für die Erwärmung der Bauelemente dar. Die Einschaltverluste von
Dioden werden im Allgemeinen vernachlässigt, weil sie deutlich geringer als die
Ausschaltverluste sind. Da die SiC-Diode jedoch extrem kleine Ausschaltverluste besitzt,
sollen die Einschaltverluste an dieser Stelle ebenfalls betrachtet werden.
12
150
9
125
6
100
3
75
0
50
Si
-3
Ud[V]
Id/[A]
Mit Hilfe einer Chopperschaltung wurden der Verlauf von Strom und Spannung beim
Einschalten einer SiC-Schottkydiode und einer Si-Freilaufdiode gemessen. Für eine
optimierte Auflösung der Spannungsmessung wurde dieser Versuch bei kleiner
Zwischenkreisspannung von ca. 45V durchgeführt, um eine Übersteuerung der
Eingangsverstärker des Oszilloskops zu vermeiden.
25
-6
0
SiC
-9
-25
-12
-50
0
100
200
300
400
500
600
700
800
900
t/[ns]
Abbildung 38: Einschaltverhalten der Si-Diode (rot) und der SiC-Schottkydiode (grün)
Das Einschaltverhalten der Dioden ist aus Abbildung 38 ersichtlich, wobei die oberen beiden
Kurven jeweils den Strom, die unteren beiden Kurven jeweils die Diodenspannung
darstellen. Zunächst leitet der IGBT des Halbbrückenzweiges, die Zwischenkreisspannung
von ca. 45V liegt an der Diode an. Mit dem Beginn des Abschaltvorganges nimmt der IGBT
Spannung auf, analog sinkt die Spannung an der Diode. In der Kurvenform der Spannung an
der Diode ist der charakteristische Verlauf der IGBT-Spannung erkennbar, die zunächst
langsam und dann beschleunigt ansteigt.
Mit dem Nulldurchgang der Spannung an der Diode kann die Stromkommutierung beginnen,
die sich über einen Zeitraum von etwa 100ns erstreckt. Die Si-Diode zeigt einen
ausgeprägten Spannungsabfall in Vorwärtsrichtung, um den Strom zu führen. In diesem
Zeitabschnitt ist die Ladungsträgerinjektion in der Si-Diode noch nicht vollständig erfolgt. Mit
zunehmender Zeitdauer wird die Si-Diode mehr und mehr mit Ladungsträgern
überschwemmt, so dass ihre Spannung in Vorwärtsrichtung abnimmt und schließlich ihren
statischen Endwert erreicht. Die maximale Spannungsspitze an der Si-Diode beträgt knapp
49
50V. Im Bereich der erhöhten Vorwärtsspannung treten in dieser Diode Einschaltverluste
auf, die jedoch gegenüber den Ausschaltverlusten der Si-pn-Diode unter 1% betragen und
damit so gering sind, dass sie bei der thermischen Auslegung vernachlässigt werden
können.
Bei der SiC-Schottkydiode findet keine Modulation der Leitfähigkeit statt. Der statische
Endwert wird nahezu ideal sofort beim Einschalten erreicht, ohne dass eine
Spannungsspitze erkennbar ist. Einschaltverluste sind in diesem Fall nicht messbar, die
gesamten Verluste werden über die Durchlassverluste erkannt.
2.3 Auslegung des Umrichters für verschiedene Dioden
2.3.1 Berechnung der Verlustleistung im Umrichterbetrieb
Bei der Berechnung der Verlustleistung wird auf ein Modell gemäß [17] bzw. [62]
zurückgegriffen.
2.3.1.1 Berechnung der Durchlassverluste
Bei der Berechnung der Durchlassverluste werden die gemessenen Durchlasskennlinien zu
Grunde gelegt. Der nichtlineare Verlauf der Durchlassspannung als Funktion des
Laststromes, der bei dem IGBT und der pn-Diode im Wesentlichen durch die injizierenden
p+n bzw. nn+ Übergänge und bei der Schottkydiode durch die Schottky-Barriere bestimmt
wird, soll hierbei durch eine lineare Näherung nachgebildet werden:
U CE = U CE 0 +
U CEN − U CE 0
IC
I CN
(29)
bzw. für die Diode
U D = U D0 +
U DN − U D 0
ID
I DN
(30)
Diese Näherung ist in Abbildung 39 grafisch dargestellt:
30
30
25
25
ID/[A]
40
IDN 35
IC/[A]
40
ICN 35
20
20
15
15
10
10
5
5
0
0
0
1
UCE0
2
3
UCE/[V]
4
UCEN
5
0
0.4
0.8
1.2
1.6
UD0 U/[V]
Abbildung 39: Linearisierung der Durchlasskennlinien von IGBT und Diode
50
2
UDN
Mit diesen Diagrammen kann zu jedem Zeitpunkt der augenblickliche Wert der
Durchlassverluste in Abhängigkeit vom Strom berechnet werden.
Der Stromverlauf in einem Halbleiterschalter ergibt sich aufgrund der Modulation. Die
wesentlichen Zeitverläufe bei Anwendung der Sinus-Dreieck-Modulation sind in Abbildung 40
dargestellt:
δ
φ
1.1
tp
1
M
spannung
0.5
i
strom
i
0
pulsed
T1
i
i
0.5
1
1.1
0
0.2
0.4
0.6
0.8
0
1
winkel
1.2
1.4
1.6
1.8
2
2
i
π
Abbildung 40: Zeitlicher Verlauf von Grundschwingungsspannung (rot), gepulster Spannung
(magenta), Ausgangsstrom (cyan) und IGBT-Strom (blau) über einer Periode des
Grundschwingungsstromes
In Abbildung 40 ist eine Grundschwingungsperiode des Ausgangsstromes einer
Wechselrichterphase dargestellt. Mit einem Phasenwinkel φ folgt dieser Ausgangsstrom der
Grundschwingung der Spannung nach. Die Spannung wird durch Pulsweitenmodulation des
Wechselrichters bereitgestellt, wobei in den Zeiträumen, in denen die gepulste
Ausgangsspannung in Abbildung 40 den Wert „1“ annimmt, die entsprechende
Wechselrichterausgangsphase durch Einschalten des oberen IGBTs T1 mit dem positiven
Zwischenkreisspannungspotenzial
verbunden
wird;
analog
wird
die
Wechselrichterausgangsphase mit dem negativen Zwischenkreisspannungspotenzial
verbunden, wenn die gepulste Spannung den Wert „-1“ annimmt.
Durchlassverluste in T1 treten auf, solange T1 eingeschaltet ist und Strom führt. In
Abhängigkeit des Modulationsgrades M und des Phasenwinkels φ berechnet sich die relative
Einschaltdauer δ innerhalb einer Modulationsperiode tp als Funktion des Winkels α des
Laststromes zu:
51
δ =
1
(1 + Μ sin (α + φ ))
2
(31)
Hierbei ist bereits berücksichtigt, dass die Spannungssollwertkurvenform eine Sinusfunktion
mit relativem Scheitelwert M darstellt; grundsätzlich ist Gl. (31) auch auf andere
Sollwertkurvenformen übertragbar.
In den Zeiten der positiven Stromhalbschwingung, in denen T1 nicht leitet, fließt der
Laststrom durch die gegenüberliegende Diode D2. Während der negativen Stromhalbwelle
führen T2 und D1 den Strom, so dass während dieser Halbwelle im betrachteten IGBT T1
keine Durchlassverluste anfallen.
Innerhalb einer Modulationsperiode tp der positiven Stromhalbwelle führt T1 während seiner
relativen Einschaltdauer δ den Laststrom, für die verbleibende Zeit der Modulationsperiode
ist T1 ausgeschaltet und somit stromlos. Während der Einschaltdauer δ wird angenommen,
dass sowohl die Stromamplitude ICT1 als auch der Wert der Durchlassspannung UdT1
konstant sind. Für die Verlustenergie in T1 während einer Modulationsperiode gilt somit:
⎞
⎛
U
− U CE 0
1
I C ⎟⎟ I C (1 + M sin (α + φ )) t p
E dT 1 = U dT 1 I CT 1 δ t p = ⎜⎜ U CE 0 + CEN
I CN
2
⎠
⎝
(32)
Der Stromverlauf im Motor wird als sinusförmig angenommen
I C (α ) = I C max sin α
(33)
Dadurch ergibt sich die Durchlassverlustenergie in einer Modulationsperiode zu
⎞
⎛
U
− U CE 0
1
E dT 1 (α ) = ⎜⎜ U CE 0 + CEN
I C max sin α ⎟⎟ I C max sin α (1 + M sin (α + φ )) t p
I CN
2
⎠
⎝
(34)
Für die Berechnung der Durchlassverluste kann die Modulationsperiode tp beliebig klein
angenommen werden, ohne dass sich die Gesamtverlustenergie innerhalb der
Stromhalbwelle ändert, da sich die Anzahl der Modulationsperioden innerhalb der
Stromhalbwelle gleichermaßen erhöht. Dadurch geht die Modulationsperiode tp in eine
differentielle Modulationsperiode dtp über. Diese kann als Funktion des Winkels α des
Laststromes ausgedrückt werden:
dt p =
dα
T
2π
(35)
Die Verlustleistung während einer Stromgrundschwingung ergibt sich dann als Integral über
die Verlustenergien aller differentiellen Modulationsperioden, bezogen auf die
Grundschwingungsdauer T:
PdT 1
⎛ T
π⎜
I
1
= • ∫ ⎜ 2 ⋅ 2 ⋅ π C max
T 0⎜
⎝ ⋅ (1 + M sin (α
2
⎞⎞
⎛ U CEN − U CE 0
⎜⎜
I C max sin α + U CE 0 sin α ⎟⎟ ⎟
I CN
⎠ ⎟dα
⎝
⎟
+ φ ))
⎠
Durch Integration von Gl. (36) ergibt sich:
52
(36)
⎛⎛ 1
PdT 1 = I C max U CE 0 * ⎜⎜ ⎜⎜
⎝⎝ 2π
2
⎞ M cos φ ⎞ U CEN − U CE 0
⎟+
⎟⎟ +
I
C
max
⎟
8
I CN
⎠
⎠
⎛
⎜
•⎜
⎜
⎜
⎝
1 M cos φ ⎞⎟⎟
+
8
3 π ⎟⎟⎠
(37)
Die Berechnung der Durchlassverluste der Diode erfolgt analog. Der Unterschied besteht
darin, dass die Diode während der Modulationsperiode tp genau zu dem Zeitpunkt leitet, in
dem der IGBT ausgeschaltet ist. Statt Gl. (31) ergibt sich für die Leitdauer der Diode
δ =
1
(1 − Μ sin (α + φ ))
2
(38)
und folgerichtig für die Durchlassverluste der Diode:
⎛⎛ 1
PdD 2 = I C max U D 0 ⎜⎜ ⎜⎜
⎝⎝ 2π
2
⎞ M cos φ ⎞ U DN − U D 0
⎟+
⎟⎟ −
I
C
max
⎟
8
I CN
⎠
⎠
⎛
⎜
•⎜
⎜
⎜
⎝
1 M cos φ ⎞⎟⎟
−
8
3 π ⎟⎟⎠
(39)
2.3.1.2 Berechnung der Schaltverluste
Neben den Durchlassverlusten bilden die Schaltverluste der Leistungshalbleiter eine zweite
Art von Verlusten, die insbesondere für hohe Schaltfrequenzen wichtig und mitunter
dominant gegenüber den Durchlassverlusten werden. Für die Berechnung der Schaltverluste
wird wiederum die Stromkurvenform aus Abbildung 40 herangezogen [112].
Innerhalb einer Modulationsperiode wechselt das Potenzial der betrachteten Ausgangsphase
zweimal seine Polarität.
UA
T1
D1
UZK
CZK
UZK
T2
D2
0
UA
tp
t
Abbildung 41: Schaltvorgänge innerhalb einer Modulationsperiode
Ist der Ausgangsstrom der Wechselrichterphase positiv, so treten innerhalb der betrachteten
Modulationsperiode tp am Leistungshalbleiter T1 je einmal Ein- und Ausschaltverluste auf.
Dies gilt auch für die Diode D2. Analog treten die Schaltverluste in der negativen
Stromhalbwelle in T2 und D1 auf.
53
Zur Berechnung der Schaltverluste über eine Grundschwingung des Ausgangsstromes
werden zunächst die Ein- und Ausschaltverlustenergien von Transistor und Diode bei einer
festen Zwischenkreisspannung in Abhängigkeit vom Ausgangsstrom bei verschiedenen
Lastströmen gemessen. Aus den gemessen Stützstellen wird anschließend nach der
Methode der kleinsten Abstandsquadrate eine Ausgleichskurve durch die Messstellen gelegt.
Als Kurvenform für die Ausgleichskurve hat sich in der Praxis ein Polynom zweiter Ordnung
bewährt. Die Schaltverlustenergie in Abhängigkeit des Stromes ergeben sich somit zu:
(40)
E s ( I ) = K 0 + K1 ⋅ I + K 2 ⋅ I 2
Analog zu den Durchlassverlusten treten auch die Schaltverluste in einem
Leistungshalbleiter nur während einer Halbwelle des Grundschwingungsstromes auf. Bei
einem sinusförmigen Verlauf des Ausgangsstromes ergeben sich die Schaltverluste in einem
Leistungshalbleiter somit zu
Ps =
1
2π
π
∫f
= fs (
( Κ 0 + Κ1 ⋅ Ι C max sin α + K 2 ⋅ I C max sin 2 α ) dα
2
s
0
(41)
K 0 K1
K2
2
+
I C max +
I C max )
π
2
4
Mit dieser Formel können die Schaltverluste für den Umrichter berechnet werden. Es ist
leicht zu erkennen, dass sie unabhängig vom Leistungsfaktor sind, da die Schaltverluste in
den Bauteilen immer auftreten, unabhängig davon, ob das anschließende Leitintervall für
den IGBT oder die Diode länger ist.
Eine Randbedingung für eine Berechnung der Schaltverlustleistung nach Gl. (41) besteht
darin, dass davon ausgegangen wird, dass während der gesamten Grundschwingung
Schalthandlungen stattfinden und die Schaltfrequenz zeitinvariant ist.
Dies wird zum Beispiel dann verletzt, wenn der Umrichter nahe an seinem maximalen
Aussteuergrad arbeitet und im Bereich des Maximums der Grundschwingung der
Ausgangsspannung einzelne Schalthandlungen aufgrund der Verletzung von Mindestzeiten
nicht ausgeführt werden. Soll dieser Effekt mit berücksichtigt werden, müssen die
Schaltverluste für jede einzelne tatsächliche Schalthandlung ermittelt werden. Vorzugsweise
ist dies mit Hilfe eines Simulationsprogrammes durchzuführen.
Ein weiterer Anwendungsfall, in dem die oben geforderte Randbedingung verletzt wird, ist
dann gegeben, wenn die Schaltfrequenz nicht wesentlich höher als die
Umrichterausgangsfrequenz gewählt wird. Ein solcher Betrieb ist von Umrichtern mit sehr
hoher Ausgangsleistung bekannt. Bei diesen Anwendungen kann es vorkommen, dass
systematisch in bestimmten Bereichen der Grundschwingung des Ausgangsstromes keine
Schalthandlungen vorgenommen werden. Im vorliegenden Fall, in dem der Umrichter für die
Verwendung eines Sinus-Ausgangsfilters optimiert wird, ist für ein optimiertes Filterdesign
die Schaltfrequenz deutlich höher als die Umrichterausgangsfrequenz, wie in Kap. 3 erläutert
wird.
2.3.1.3 Verluste bei Ausgangsfrequenz 0Hz
Mit Gl. (41) und Gl. (37) bzw. Gl. (39) können für jeden Leistungshalbleiter die Verluste über
einer Grundschwingungsperiode berechnet werden. Diese Berechnung ist zutreffend,
solange die Ausgangsfrequenz des Umrichterausgangsstromes so hoch ist, dass sich
54
innerhalb einer Grundschwingungsperiode die Temperatur eines Halbleiterchips nicht
wesentlich ändert. Denn durch die Integration in den genannten Gleichungen wird ein
Mittelwert über die in der betrachteten Periode anfallenden Verluste errechnet. Für die
stationäre Betrachtung des Umrichters bei hoher Ausgangsfrequenz, die für die meisten
Anwendungen im Vordergrund steht, ist diese Vorgehensweise geeignet, da thermische
Zeitkonstanten in der Aufbautechnik der Halbleitermodule und Umrichter diese
Mittelwertbildung vornehmen.
Die Betrachtungsweise wird unzureichend, wenn der Umrichter bei so kleiner
Ausgangsfrequenz betrieben wird, dass die Leistungshalbleiter und deren Umgebung
innerhalb einer Grundschwingungsperiode ihre Temperatur wesentlich ändern, d.h. die
Periodendauer der Grundschwingung in den Bereich der thermischen Zeitkonstanten des
Halbleiters kommt. Dieser Betriebszustand wird anhand eines in der Stromrichtertechnik
üblichen Raumzeigermodells erläutert.
V
I
U
W
Abbildung 42: Raumzeiger des Scheitelwertes des Ausgangsstromes in einem
ständerbezogenen Koordinatensystem
In Abbildung 42 ist der Raumzeiger des Scheitelwertes des Ausgangsstromes dargestellt.
Die Raumzeigerdarstellung von Größen basiert auf der Theorie elektrischer Maschinen,
wobei als anschauliche Erklärung das Diagramm als Schnitt durch den Stator einer
elektrischen Maschine mit Blick in Richtung der Maschinenachse betrachtet werden kann.
In Abbildung 42 ist ein stehendes, statorbezogenes Koordinatensystem gezeigt. In diesem
Koordinatensystem rotiert der Stromzeiger I mit der Kreisfrequenz des Ausgangsstromes
gegen den Uhrzeigersinn. Der augenblickliche Betrag der Ströme in den einzelnen Phasen
U, V und W ergibt sich durch die Projektion des Stromzeigers I auf die jeweilige Achse. Bei
konstantem Betrag und konstanter Kreisfrequenz des Stromzeigers ergeben sich somit die
bekannten dreiphasigen sinusförmigen Ausgangsströme des Umrichters.
Ist die Kreisfrequenz des Stromzeigers I sehr klein, so verweilt der Stromzeiger sehr lange in
Richtung einer Achse. In diesem Fall ist die Temperatur an einem Halbleiterchip über eine
Grundschwingungsperiode nicht mehr konstant. Die Berechnung der Chiptemperatur ist in
diesem Fall nicht mehr über einfache statische Gleichungen möglich, sondern es ist eine
transiente Simulation mit einem thermischen Modell erforderlich.
Je geringer die Ausgangsfrequenz wird, desto länger verweilt der Stromzeiger an einer Stelle
und
desto
größer
wird
die
Temperaturdifferenz,
die
innerhalb
einer
55
Grundschwingungsperiode am Halbleiterchip auftritt. Im Extremfall ist die Ausgangsfrequenz
gleich null, so dass der Stromzeiger steht. Für den Umrichter bedeutet dies, dass an seinem
Ausgang ein Gleichstrom fließt. Abhängig von den Anforderungen der Regelung kann der
Stromzeiger nun genau in der Richtung einer Motorphase, z.B. der Phase U stehen. In
diesem Fall fließt in der Phase U dauerhaft der Scheitelwert des Ausgangsstromes als
Gleichstrom. Durch die Projektion des Stromzeigers auf die Phasen V und W ergibt sich,
dass in diesen jeweils die Hälfte des Scheitelwertes des Ausgangsstromes in negativer
Richtung fließt.
Î
U
V
W
M
Î/2
Î/2
Abbildung 43 Maximale Umrichterausgangsströme bei einer Ausgangsfrequenz von 0Hz
Dieser Betriebspunkt ist wieder stationär und kann somit auch einfach berechnet werden.
Zur Ermittlung des worst case kann somit auf die transiente Simulation verzichtet werden.
Der Betrag des Stromzeigers wird durch das Drehmoment bestimmt, das an der Motorwelle
abgenommen wird, und entspricht im worst case dem Scheitelwert des Stromes. Mit der
Auslegung des Umrichters auf diesen Betriebspunkt sind alle anderen Betriebspunkte kleiner
Schaltfrequenz mit abgedeckt.
Bei dem Betrieb mit Ausgangsfrequenz 0Hz werden am Ausgang des Frequenzumrichters
näherungsweise nur Nullzeiger ausgegeben, da die Ausgangsspannung ebenfalls null ist.
Unter Nullzeigern werden die Schaltzustände verstanden, bei denen alle drei
Umrichterausgangsphasen gleichzeitig entweder mit dem positiven (positiver Nullzeiger)
oder dem negativen (negativer Nullzeiger) Zwischenkreispotenzial verbunden werden, so
dass sich zwischen den Phasen die Spannung null ergibt. Alle anderen Schaltzustände
werden als aktive Zeiger bezeichnet; diese erzeugen eine treibende Spannung zwischen den
Phasen des Motors. Im Betriebspunkt der Umrichterausgangsfrequenz null werden diese
aktiven Zeiger nur zur Deckung der ohmschen Verluste im Stator der Maschine, den
Motorleitungen und den Durchlassverlusten im Wechselrichter benötigt. Bei Sinus-DreieckModulation und Raumzeigermodulation werden der positive und der negative Nullzeiger
abwechselnd mit einer Leitdauer von je 50% innerhalb der Modulationsperiode angelegt.
Die Berechnung der Durchlassverluste ergibt sich somit in der Phase U, in der der maximale
Strom steht, zu:
PdTU 0 = δ (U CE 0 +
U CEN − U CE 0
I C max ) I C max
I CN
= 0.5 ⋅ U CE 0 I C max
(42)
− U CE 0
U
2
+ 0.5 ⋅ CEN
I C max
I CN
Analog können die Durchlassverluste in den Transistoren der Phasen V und W berechnet
werden, in denen jeweils die Hälfte des maximalen Stromes fließt:
56
PdTV 0 = PdTW 0 = 0.5 ⋅ U CE 0
I C max U CEN − U CE 0 I C max
+
⋅
I CN
2
4
2
(43)
Für die Durchlassverluste in den Dioden ergibt sich analog:
PdDU 0 = (1 − δ ) (U D 0 +
U DN − U D 0
I D max ) I D max
I DN
= 0.5 ⋅ U D 0 I D max + 0.5 ⋅
PdDV 0 = PdDW 0 = 0.5 ⋅ U D 0
(44)
U DN − U D 0
2
I D max
I DN
I D max U DN − U D 0 I D max
+
I DN
2
4
2
(45)
Die Schaltverluste im Betrieb bei einer Ausgangsfrequenz von 0Hz können auf Basis von Gl.
(40) für die Phase U berechnet werden:
(46)
2
PsU 0 = f s ( K 0 + K 1 ⋅ I C max + K 2 ⋅ I C max )
Für die Werte K0, K1 und K2 sind jeweils die Koeffizienten der Ausgleichsparabeln der
gemessenen Schaltverluste aus Kap. 2.3.1.2 für IGBT bzw. Diode zu verwenden.
Analog lassen sich die Schaltverluste der stromführenden Bauelemente aus den Phasen V
und W berechnen:
2
PsV 0 = PsW 0
I
I
= f s ( K 0 + K 1 ⋅ C max + K 2 ⋅ C max )
2
4
(47)
2.3.1.4 Verlustoptimierung für kleine Ausgangsfrequenzen
Der Betriebspunkt bei Ausgangsfrequenz 0 stellt für die Bauelemente, die in der Phase mit
dem höchsten Strombetrag den Strom führen, eine sehr hohe Belastung dar, die für die
Dimensionierung des Frequenzumrichters sehr wichtig ist. Bezüglich der Durchlassverluste
ist aus Gl. (42) und Gl.(44) ersichtlich, dass die relative Leitdauer des oberen und unteren
Nullzeigers eine Möglichkeit darstellt, die Verluste in einem einzelnen Bauelement gezielt zu
reduzieren oder zu erhöhen.
Für einen Wechselrichter aus Si-IGBTs und SiC-Freilaufdioden liegt nun die Situation vor,
dass die Fläche der Freilaufdioden sehr viel teuerer ist als die Fläche der IGBTs. In diesem
Fall ist es wünschenswert, die am stärksten belastete Diode so weit wie möglich zu
entlasten, wobei eine Mehrbelastung des IGBT bzgl. der Kosten weniger relevant ist. In
anderen Anwendungen, die beispielsweise IGBTs mit einer Trench-Technologie einsetzen,
die wesentlich teuerer als eine einfache Dioden-Technologie ist, kann dies umgekehrt sein,
die allgemeine Motivation zur gezielten Entlastung eines einzelnen Bauelementes ist jedoch
identisch.
Eine Entlastung der Diode, die den höchsten Phasenstrom zu führen hat, kann dadurch
erfolgen, dass die Einschaltdauer dieser Diode reduziert wird. Eine minimale Einschaltdauer
57
ergibt sich durch die Tatsache, dass durch diese Maßnahme die Verluste in den Dioden der
anderen beiden Phasen ansteigen. Eine ideale Einschaltdauer ergibt sich, wenn die Verluste
der Dioden mit den beiden höchsten Phasenströmen gleich werden.
1
0.866
0.5
Iu
γ
Iv
γ
0
Iw
γ
0.5
1
1
0
5
0
10
15
20
γ
25
30
30
Abbildung 44: Phasenströme bei unterschiedlichen Stromwinkeln
Für eine vollständige Betrachtung der möglichen Phasenströme am Umrichterausgang
genügt ein Ausschnitt von 30° für mögliche Stromwinkel, da sich dieser Ausschnitt innerhalb
der 360° für eine Umdrehung lediglich für alle Leistungshalbleiter wiederholt.
In Abbildung 44 ist der Strom in Phase V betragsmäßig maximal. Zählt man aus dem
Umrichter herausfließende Ströme positiv, so wird in diesem Umrichter bei konventionellen
Modulationsverfahren die obere Diode der Phase V am stärksten belastet. Der relevante
Auslegungspunkt für die Leistungshalbleiter des Umrichters liegt bei 30°, da bei dieser
Rotorlage der maximale Strom in dieser Diode fließt.
Aus Abbildung 44 ist auch sofort die Grenze eines Verfahrens zur Optimierung der Verluste
durch geschickte Wahl des Nullzeigers zu sehen. Bei 0° sind die Ströme in den Phasen V
und W betragsmäßig gleich. In diesem Punkt beträgt der ideale Aussteuergrad 50% wie bei
konventionellen Verfahren, da eine Entlastung der Diode in Phase V sofort eine
Überbeanspruchung der Diode in Phase W verursacht.
Die ideale relative Leitdauer der Diode in Phase V in Abhängigkeit des Stromwinkels γ
berechnet sich aus dem Verlustverhältnis:
δ V (γ ) =
PDW (γ )
PDV (γ ) + PDW (γ )
(48)
Bezogen auf die Verlustleistung bei konventioneller Modulation ergibt sich die verbleibende
Verlustleistung in der Diode zu dem doppelten der idealen Leitdauer. Der Faktor 2 ergibt sich
aus der Tatsache, dass bei konventioneller Modulation das Tastverhältnis 0.5 beträgt.
58
Betrachtet man diese Verluste für Schottkydioden, so treten nur Durchlassverluste auf, da
die Schottkydiode keine Schaltverluste verursacht. Mit der Linearisierung der
Durchlassverluste nach Gl. (30) bestehen die Durchlassverluste P(I) der Diode bei
konstantem Strom aus einem linearen Term, der durch die Schwellenspannung bestimmt
wird, und einem quadratischen Term, der durch den differentiellen Widerstand bestimmt
wird.
Wie hoch die mögliche Einsparung ist, hängt demnach von der Durchlasskennlinie der
verwendeten Bauelemente ab. Die Grenzwerte können jedoch allgemein berechnet werden.
Ein Grenzwert ergibt sich, indem man ein Bauelement annimmt, das nur eine
Schwellenspannung und einen differentiellen Widerstand von 0 besitzt. Ein solches Bauteil
ist nicht realistisch. Näherungsweise wird dieses Verhalten erreicht, wenn man eine Diode
mit sehr geringer Stromdichte betreibt. Bei diesem Bauelement steigen die Durchlassverluste
linear mit dem Strom.
Den zweiten Grenzwert bildet ein Bauelement mit rein ohmschem Verhalten. Diese Kennlinie
wird von einem unipolaren Halbleiterschalter, z.B. einem MOSFET oder einem JFET
erreicht. Bei einem solchen Bauelement steigen die Verluste quadratisch mit dem Strom.
In Abhängigkeit des Stromwinkels sind die verbleibenden Verlustleistungen für die beiden
Grenzbauelemente dargestellt:
1
0.9
0.8
Pquad
Plin
γ
γ 0.7
0.6
0.5
0.4
0.4 0.3
0
0
5
10
15
20
γ
25
30
30
Abbildung 45: Verbleibende Verlustleistung bezogen auf den Auslegungswert bei
konventioneller Modulation
Für die Auslegung eines Umrichters ist aus Abbildung 45 der ungünstigste Fall auszuwählen.
Bei konventioneller Modulation ist dieser Auslegungspunkt bei einem Stromwinkel von 30°,
weil dort ein Phasenstrom maximal wird.
Es ist zu erkennen, dass bei dem verbesserten Modulationsverfahren die maximalen
Verluste bei einem Stromwinkel von 30° stark reduziert werden können, so dass dieser
Stromwinkel nicht mehr die Auslegung bestimmt. Der auslegungsrelevante Stromwinkel liegt
mit dem verbesserten Verfahren bei 0°. In diesem Betriebspunkt sind die Ströme in den
59
Phasen V und W identisch, so dass das neuartige Modulationsverfahren an diesem Punkt
keinen weiteren mehr Vorteil bringt.
Abhängig von der Kennlinie kann die auslegungsrelevante Verlustleistung der verwendeten
Diode
im
Vergleich
zu
konventioneller
Sinus-Dreieck-Modulation
oder
Raumzeigermodulation auf Werte zwischen 75% und 86% abgesenkt werden.
Aus Abbildung 45 ist weiterhin zu erkennen, dass bei dem Bauelement mit hohem
ohmschem Anteil in der Kennlinie die verbleibende Verlustleistung stärker abgesenkt werden
kann. Dies ist dadurch zu erklären, dass sich die Reduzierung des Stromwertes in diesem
Fall stärker bemerkbar macht.
Bei Umrichtern ohne Sinus-Ausgangsfilter kann die starke thermische Belastung einzelner
Bauelemente bei Ausgangsfrequenz null durch eine Absenkung der Schaltfrequenz reduziert
werden. Bei dem Demonstratorumrichter ist dies aus folgenden Gründen nicht möglich:
a) Bei Umrichtern mit Sinusfilter besteht die Gefahr, dass die abgesenkte
Schaltfrequenz in den Bereich der Resonanzfrequenz des Sinusfilters trifft und
dieses anregt.
b) Für SiC-Schottkydioden ist die Reduzierung der Schaltfrequenz wenig hilfreich, weil
die Schottkydioden nahezu keine Schaltverluste verursachen und ihre hohe
thermische Belastung allein aus Durchlassverlusten resultiert. Lediglich eine
indirekte Entlastung der SiC-Diode durch Absenkung des Temperaturniveaus des
Kühlkörpers wäre möglich, weil die IGBTs bei der geringeren Schaltfrequenz weniger
Verluste erzeugen.
Aus diesen Gründen ist die Auswahl der Nullzeiger nach dem Kriterium der thermischen
Belastung der Halbleiter für den Demonstratorumrichter besonders attraktiv.
2.3.2 Thermisches Modell
Für die rechnerische Auslegung eines Umrichters ist ein thermisches Modell erforderlich, das
von den berechneten Halbleiterverlusten auf deren Erwärmung schließen lässt ([64], [127]).
Obwohl der primäre Fokus im vorliegenden Fall auf den relativen Unterschieden zwischen
einzelnen Halbleiterlösungen liegt, sollen dennoch möglichst anwendungsnahe
Randbedingungen gewählt werden.
Das stationäre thermische Modell basiert auf einem Ersatzschaltbild nach Abbildung 46. In
diesem werden Temperaturen als Spannungspotenziale, Verlustleistungen als Stromquellen
und thermische Widerstände von Komponenten als Widerstand dargestellt:
Tjt
PD
RthjhT
Tjd
RthjhD
Th
PT
Th
5*PT
5*PT
Rthha
Ta
Abbildung 46: Thermisches Ersatzschaltbild des Umrichters beim Betrieb mit hoher
Ausgangsfrequenz
60
Durch den Transistor werden in das thermische Modell die Verlustleistung PT, durch die
Diode die Verlustleistung PD eingespeist. Sowohl für den IGBT als auch für die Diode wird
die Verlustleistung PT bzw. PD durch die Addition der Schalt- und Durchlassverluste nach
obigen Gleichungen berechnet.
Die Halbleiter selbst werden durch einen thermischen Widerstand RthjhT und RthjhD
modelliert. Über diesem thermischen Widerstand fällt in dem thermischen Ersatzschaltbild
nach Abbildung 46 ein Temperaturhub ab. Dieser repräsentiert den Temperaturhub der
Sperrschicht des Halbleiterchips gegenüber der Oberfläche des Kühlkörpers. Es wird dabei
angenommen, dass innerhalb des Halbleitermoduls keine thermische Kopplung zwischen
den einzelnen Chips besteht, sondern der Wärmeaustausch allein über die Bodenplatte
stattfindet. Diese Vereinfachung ist in der Praxis nicht ganz erfüllt, weil über die Keramik und
die Bodenplatte des Halbleitermoduls ein gewisser Wärmeaustausch stattfinden kann.
Die Oberfläche des Kühlkörpers wird mit der einheitlichen Temperatur Th angenommen.
Auch dies stellt eine Vereinfachung dar, weil die Oberfläche des Kühlkörpers somit unendlich
gut leitend modelliert wird, in der Realität ist ein geringer Temperaturgradient auf der
Oberfläche des Kühlkörpers vorhanden. Die beiden beschriebenen Vereinfachungen wirken
gegenläufig und kompensieren sich somit teilweise.
Die Halbleiterverluste, die z.B. für den Transistor durch Gl. (37) und Gl. (41) berechnet
werden, beziehen sich nur auf einen Transistor des Wechselrichters. Für die Erwärmung der
Bodenplatte gegenüber Kühlkörper und Umgebungstemperatur müssen jedoch alle Chips
berücksichtigt werden. Dies erfolgt durch eine Superposition mit zwei
weiteren
Verlustleistungsquellen, die jeweils die Verlustleistung der anderen fünf Chips der
Wechselrichterbrücke einbringen. Bei hoher Ausgangsfrequenz ist diese Vorgehensweise
korrekt, da alle Halbleiterchips identische Verluste verursachen.
Die gesamten Verluste aller Halbleiterchips bewirken einen Temperaturhub der Oberfläche
des Kühlkörpers gegenüber der Umgebungstemperatur. Dieser Übergangswiderstand zur
umgebenden Kühlluft wird durch Rthha modelliert.
Wie in Kapitel 2.3.1.3 gezeigt, sind die Halbleiterverluste bei kleiner Ausgangsfrequenz für
die Chips unterschiedlicher Phasen nicht mehr identisch. Wird der Umrichter bei einer
Ausgangsfrequenz von 0Hz betrachtet, so sind nur noch 6 statt 12 Halbleiter mit Verlusten
beaufschlagt, da die Stromrichtung sich nicht mehr ändert. Für den worst case, in dem der
Stromzeiger nach Abbildung 42 genau auf einer Phase steht, ist der Betrag des Stromes in
den beiden anderen Phasen identisch. Das modifizierte Ersatzschaltbild für diesen
Betriebspunkt ergibt sich zu:
TjTU
PDU
RthjhT
TjDU TjTV
TjDV
RthjhT
RthjhD
RthjhD
Th
PTU
PDV
PTV
PTV
PDV
Rthha
Ta
Abbildung 47: Thermisches Ersatzschaltbild bei Ausgangsfrequenz 0Hz
61
Die Parameter des thermischen Modells können durch eine standardmäßige Rth-Messung
bestimmt werden. Für die für diese Messung erforderliche Bestimmung der
Halbleitertemperatur wird der Effekt ausgenutzt, dass sich die Schwellenspannung am pnÜbergang eines Leistungshalbleiters mit der Temperatur verändert.
Nach [109] gilt für die Schleusenspannung an einem pn-Übergang:
p+ N D
kT
• ln
U=
2
q
ni
p+:
ND:
n i:
k:
q:
T:
mit
(49)
Dotierungskonzentration im p-Gebiet
Dotierungskonzentration in der schwach dotierten Mittelschicht
intrinsische Ladungsträgerkonzentration
Boltzmann-Konstante
Elementarladung
absolute Temperatur in Kelvin
Mit steigender Temperatur nimmt die Anzahl der intrinsischen Ladungsträger stark zu. Es
gilt:
2
ni = N c N v e
mit:
−
Eg
(50)
kT
Nc, Nv:
Eg:
Anzahl der möglichen Zustände im Leitungs- und Valenzband
Bandabstand
Setzt man Gl. (50) in Gl. (49) ein, so ergibt sich für die Schwellenspannung:
U=
Eg
q
−
N N
kT
• ln +c v
q
p ND
(51)
Die effektiv vorliegenden Dotierungskonzentrationen sind immer geringer als die Anzahl der
möglichen Zustände im Leitungs- bzw. Valenzband, wodurch der Logarithmusterm in Gl. (51)
immer einen positiven Wert liefert. Somit ist mit steigender Temperatur eine Abnahme der
Schwellenspannung messbar.
Für die Bestimmung des thermischen Widerstandes wird die Schwellenspannung in
Abhängigkeit von der Temperatur zunächst in einer Eichkurve aufgezeichnet. Der
Messaufbau ist in Abbildung 48 skizziert:
10mA
DUT
Heizplatte
Spannungsmessung
Temperaturmesspunkt
Abbildung 48: Messaufbau für die Eichung Chiptemperaturerfassung
62
Bei der Eichmessung wird das auch als DUT (device under test) bezeichnete zu messende
Halbleiterbauelement (in Abbildung 48 ist exemplarisch eine Diode dargestellt) auf einer
Heizplatte montiert. Mit dieser Heizplatte wird eine definierte Temperatur eingestellt. Das
DUT wird mit einem definierten Messstrom bestromt und gleichzeitig wird die Spannung am
DUT erfasst. Dies wird für den gesamten zu betrachtenden Temperaturbereich durchgeführt,
so dass als Ergebnis eine Messkurve der Durchlassspannung als Funktion der Temperatur
vorliegt.
Der Messstrom ist so zu wählen, dass er eine möglichst geringe zusätzliche Erwärmung des
DUT erzeugt, da diese als Fehler in das Messergebnis eingeht. Im vorliegenden Fall einer
40A bzw. 100A-Diode wurde ein Messstrom von 10mA gewählt. Die Erwärmung durch
diesen Messstrom ist < 0,01K.
Nach der Eichung erfolgt die eigentliche Messung des thermischen Widerstandes. Bei dieser
Messung wird gleichzeitig der thermische Widerstand des Kühlkörpers und des
Halbleitermoduls erfasst.
200A
10mA
Schalter
DUT
Spannungsmessung (Tj)
Kühlkörper
Temperaturmesspunkt
Kühlkörper
(Th)
Temperaturmesspunkt
Umgebungstemperatur
(Ta)
Abbildung 49: Aufbau zur Messung des thermischen Widerstands
Bei der Messung wird der Halbleiter auf den später verwendeten Kühlkörper montiert. In
Abbildung 49 ist exemplarisch eine Diode eingezeichnet, für einen IGBT erfolgt die Messung
identisch. Über eine Hochstromquelle wird eine definierte, konstante Verlustleistung PV in
den Halbleiter eingebracht, die diesen erwärmt. Der Betrag der eingebrachten
Verlustleistung ist theoretisch beliebig, zur Reduzierung von Fehlern soll diese
Verlustleistung jedoch in der gleichen Größenordnung liegen wie später beim
Umrichterbetrieb.
Wie in Abbildung 46 gezeigt, wird in dem Halbleitermodul eine ideale thermische Kopplung
der einzelnen Verlustleistungsquellen auf der Oberfläche des Kühlkörpers angenommen. Um
dies in der Messung möglichst realistisch nachzubilden, wird die Verlustleistung nicht nur in
den DUT-Halbleiterchip eingebracht, an dem die Durchlassspannung gemessen wird,
sondern in alle IGBT- bzw. Diodenchips. Mit dieser Maßnahme wird eine gleichmäßige
63
Erwärmung des Halbleitermoduls während der Messung erreicht, die auch im späteren
standardmäßigen Betrieb vorliegt.
Nachdem ein stabiler thermischer Zustand erreicht ist, wird die Hochstromquelle
abgeschaltet und unmittelbar danach die Messstromquelle zugeschaltet. Nach der
Umschaltung erfolgt in möglichst kurzer Zeit die Messung der Durchlassspannung am DUT.
Der Zeitbereich der Umschaltung muss so kurz sein, dass in dieser Zeit keine nennenswerte
Abkühlung des DUT erfolgt. Über die Eichkurve kann die Chiptemperatur des DUT bestimmt
werden. Für die IGBTs und die Freilaufdioden sind getrennte Messungen durchzuführen.
100
TjD
90
80
Th
70
T/[°C]
60
50
40
30
TjD - Th
20
10
0
1.00E-05 1.00E-04 1.00E-03 1.00E-02 1.00E-01 1.00E+00 1.00E+01 1.00E+02 1.00E+03 1.00E+04
t/[s]
Abbildung 50: Messung der Akühlkurve für Kühlkörper (blau) und Diode (rot) sowie die
Differenz der beiden Messwerte (magenta)
In Abbildung 50 sind die Messwerte der Abkühlkurve für einen Aufbau nach Abbildung 49
dargestellt. Die Umgebungstemperatur Ta ist während der gesamten Versuchsdauer
konstant und betrug in der Messung 20°. Dieser Wert stellt sich an beiden Messpunkten als
Endwert nach langer Versuchsdauer ein. Die Darstellung der Zeitskala erfolgt im
logarithmischen Maßstab, um den Bereich kurzer Zeiten besser sichtbar zu machen.
Abbildung 50 zeigt die Messung an einer Diode, analog wurde auch die Messung an einem
IGBT durchgeführt.
Die stationären thermischen Widerstände lassen sich aus der Differenz der Messwerte
unmittelbar nach der Abschaltung der Verlustleistungsquelle (t < 10-4 s) berechnen:
Rth jhT =
Rth jhD =
T jT − Th
PV
T jD − Th
PV
⋅6
(52)
⋅6
(53)
64
Rthha =
Th − Ta
PV
(54)
Mit der beschriebenen Messmethode zur Bestimmung des thermischen Widerstandes lässt
sich grundsätzlich auch das zeitveränderliche thermische Verhalten des Umrichters bei
Lastspielen exakt berechnen. In diesem Fall werden aus der Messung thermische
Zeitkonstanten ermittelt wird. Im thermischen Ersatzschaltbild werden diese durch
thermische Kapazitäten berücksichtigt. Für den Fall einer einzelnen Diode, die auf einen
Kühlkörper montiert ist und deren thermisches Verhalten durch zwei Zeitkonstanten
nachgebildet werden soll, ergibt sich damit folgendes Ersatzschaltbild [108]:
Tjd
Cthd
Rthjcd
Th
Rthha
Cthh
Pd
Ta
Abbildung 51: Physikalisches thermisches Ersatzschaltbild einer auf einen Kühlkörper
montierten Diode
Der Temperaturhub an der Diode ist die Differenz der Temperaturen von Sperrschicht und
Kühlkörper (magenta, s. Abbildung 50). Diese Differenz klingt nach einer Zeit von ca. 350ms
auf
1
ihres Anfangswertes ab. Dieser Wert stellt die Zeitkonstante
e
τ Diode = Rth jcd ⋅ Cthd
(55)
der Diode dar.
Für den Temperaturhub der Oberfläche des Kühlkörpers zur Umgebung kann die Ermittlung
der Zeitkonstante analog erfolgen. In der Messung in Abbildung 50 ist der Temperaturhub
der Kühlkörperoberfläche nach einer Zeitkonstante von
τ Kühlkörper = 150s auf 1
e
abgesunken.
Das thermische Ersatzschaltbild nach Abbildung 51 besitzt den Nachteil, dass im
allgemeinen Fall aufwändige thermische Simulationen zu seiner Berechnung erforderlich
sind. Im vorliegenden Fall der Messung aus Abbildung 50 kann jedoch die Tatsache
ausgenutzt werden, dass die beiden Zeitkonstanten τ Diode und τ Kühlkörper um etwa zwei
Größenordnungen voneinander entfernt liegen. Für schnelle Änderungen der Verlustleistung
Pd im Bereich von τ Diode kann somit Cthh als Kurzschluss betrachtet werden. Analog kann für
langsame Vorgänge im Bereich von τ Kühlkörper Cthd als hochohmig betrachtet werden.
Anschaulich bedeutet dies, dass bei einer Beaufschlagung des Halbleiterchips mit einer
sprungförmigen Verlustleistung der Temperaturhub des Halbleiterchips gegenüber der
Oberfläche des Kühlkörpers bereits seinen stationären Endwert erreicht hat, bevor die
Oberfläche des Kühlkörpers ihrerseits einen nennenswerte Temperaturhub gegenüber der
Umgebungstemperatur erfährt. Deshalb kann in diesem speziellen Fall der gesamte
transiente Wärmewiderstand als Addition der einzelnen Wärmewiderstände nach einem
65
Partialbruchnetzwerk gerechnet werden, in dem alle thermischen Kapazitäten den
thermischen Widerständen parallel liegen:
ZthgesD = Rth jhD
t
−
⎛
τ
Diode
⋅ ⎜1 − e
⎜
⎝
⎞
⎟ + Rth
ha
⎟
⎠
t
−
⎛
τ Kühlkörper
⎜
⋅ 1− e
⎜
⎝
⎞
⎟
⎟
⎠
(56)
Mit dieser Methode einer zeitabhängigen thermischen Berechnung kann der zeitliche
Temperaturverlauf in einem Lastspiel berechnet werden. Innerhalb eines Lastspiels treten
üblicherweise für eine kurze Zeit stark erhöhte Lastströme auf, gefolgt von längeren Zeiten
reduzierter Belastung. Allerdings erfordert eine zeitabhängige Berechnung nach Gl.(56)
einen erhöhten Simulationsaufwand gegenüber der einfachen stationären Berechnung, da
die einzelnen thermischen Widerstände mit der zeitveränderlichen exakten Verlustleistung
multipliziert werden.
Liegen die geforderten Zeiten eines Lastspiels weit entfernt von den ermittelten thermischen
Zeitkonstanten des Aufbaus (beispielsweise um eine Größenordnung), so kann auf die
genaue Berechnung des transienten thermischen Verhaltens verzichtet werden und es
können nur stationäre Zustände betrachtet bzw. Lastspiele mit quasistationärem Verhalten
nachgebildet werden.
Bei einem für viele Applikationen relevanten Lastspiel muss für 3s ein erhöhter Strom Imax
geführt werden, gefolgt von 297s Nennstrom Inenn. Die Zeitdauer des erhöhten Stromes liegt
um eine bzw. zwei Größenordnungen von den thermischen Zeitkonstanten des Aufbaus
entfernt. Generell kann jeder zeitabhängige Term aus Gl. (56) in diesem Fall durch zwei
mögliche Extremfälle nachgebildet werden:
a) t<< τ : In diesem Fall wird der Term zu null. Die Dauer des Lastspiels ist so kurz, dass
an dem betrachteten Element keine Temperaturerhöhung feststellbar ist.
b) t>> τ : In diesem Fall beträgt der Wert des Terms den Wert des stationären
thermischen Widerstandes, da die Exponentialfunktion zu null wird. Die Dauer des
Lastspiels ist so lange, dass das betrachtete Element vollständig durchwärmt wird
Die 3s Dauer des erhöhten Stromes bewirkt im Kühlkörper nur einen geringen,
zeitinvarianten Temperaturhub, da dessen Zeitkonstante wesentlich größer ist. Im
Halbleiterchip und im Halbleitermodul bewirkt diese Dauer jedoch eine vollständige
Durchwärmung auf Basis der Verlustwerte für den erhöhten Strom. Die maximale
Temperatur am Halbleiterchip kann somit einfach berechnet werden. Für das Beispiel der
Diode gilt:
⎛ 297 Pnenn + 3 Pmax ⎞
T jD = Ta + ⎜
⎟ Rthha + Pmax Rth jhD
300
⎠
⎝
(57)
Die Verwendung zeitabhängiger Formeln ist somit nicht erforderlich.
Für die einzelnen thermischen Widerstände der Halbleiterchips wurden folgende Werte
gemessen:
66
K
W
K
= 0.63
W
RthjhIGBT = 0.13
RthjhDiodeSi
RthjhDiodeSiC = 0.515
K
W
Bemerkenswert ist hierbei die Tatsache, dass die Si-Diode mit einer Fläche von 33,64mm2
einen höheren thermischen Widerstand besitzt als die SiC-Diode mit einer Gesamtfläche von
18,42mm2. Dies liegt in der Tatsache begründet, dass die Si-Diode aus einem einzelnen
Chip besteht, während die SiC-Diode aus einer Parallelschaltung von 6 Chips besteht, die so
weit voneinander entfernt angeordnet sind, dass sie eine wesentlich bessere
Wärmespreizung besitzen. Dies ist ein wichtiger Vorteil bei der Parallelschaltung von vielen
kleinen Chips gegenüber einem großen Chip.
Für die thermische Auslegung des Umrichters wird neben den thermischen Widerständen
der Halbleiterchips noch der thermische Widerstand des Kühlkörpers benötigt, der im Fall
des Demonstratorumrichters durch forcierte Luftkühlung mit einem Volumenstrom von 0,022
m3/s entwärmt wird. An dieser Stelle ergibt sich ein Problem, die Parallelschaltung von
Halbleitermodulen zu berücksichtigen:
Werden auf einem Kühlkörper mehrere Halbleitermodule montiert, um einen gegeben Strom
zu führen, so ist die thermische Beschreibung der Halbleitermodule einfach, da der Strom
auf die Halbleitermodule aufgeteilt werden kann. Somit können bei einer Verdopplung der
Halbleitermodule doppelt so viele Verluste eingespeist werden, um einen identischen
Temperaturhub an den Halbleitermodulen zu erzeugen. Dies ist dann möglich, wenn die
Temperaturerhöhung in einem Halbleitermodul nur vernachlässigbare Rückwirkungen auf die
Temperaturerhöhung in einem benachbarten Halbleitermodul besitzt. Im Fall des
Demonstrators ist dies erfüllt.
Bei der Betrachtung des Kühlkörpers ist diese einfache Vorgehensweise nicht mehr möglich.
Sie wäre nur dann richtig, wenn für jedes zusätzliche Halbleitermodul auch ein zusätzlicher,
identisch großer Kühlkörper und – beim angenommenen Beispiel forcierter Luftkühlung - mit
eigenem Lüfter eingesetzt werden würde. Diese Annahme ist in der Praxis jedoch nicht
realistisch. Um realistische Werte zu erhalten, muss vielmehr für jede gerechnete Anzahl von
Halbleitermodulen ein Aufbau auf einem Kühlkörper definiert und dessen thermischer
Widerstand messtechnisch erfasst werden.
Bei der thermischen Auslegung des Demonstratorumrichters soll als wesentliche Aussage
berechnet werden, wie viele Halbleitermodule einer bestimmten Ausführung für die
Realisierung der erforderlichen Betriebspunkte benötigt werden. Um den messtechnischen
Aufwand bei der Bestimmung des thermischen Widerstandes des Kühlkörpers zu begrenzen,
wurde dieser für eine Anordnung von ein, zwei und drei Halbleitermodulen gemessen. Bei
der Messung wird die Oberfläche des Kühlkörpers in etwa proportional zur Anzahl der
Halbleitermodule erhöht, der Kühlmitteldurchsatz steigt bei der Erhöhung von einem auf drei
Halbleitermodule jedoch nur um etwa den Faktor zwei an. Mit den Messwerten wird eine
Ausgleichskurve generiert, anhand derer der thermische Widerstand von Anordnungen mit
einer höheren Anzahl von Halbleitermodulen abgeschätzt wird.
67
0.12
0.1
Rthha/[K/W]
0.08
0.06
y = 0.0994x-0.7246
0.04
y = 0.1x
-1
0.02
0
0
1
2
3
4
5
6
7
8
9
10
Anzahl Halbleitermodule
Abbildung 52:Thermischer Widerstand des Kühlkörpers als Funktion der Anzahl der
Halbleitermodule bei forcierter Luftkühlung mit einem Volumenstrom von 0,022 m3/s
Die Ausgleichskurve zeigt erwartungsgemäß eine hyperbolische Form. Die drei Messwerte
wurden an Aufbauten ermittelt, die einer praxisgerechten Aufbauform entsprechen. Mit
steigender Modulanzahl ist der thermische Widerstand nicht direkt umgekehrt zur Anzahl der
verwendeten Halbleitermodule, sondern geht weniger stark zurück; die entsprechende
theoretische Kurve für umgekehrt proportionales Verhalten ist in Abbildung 52 mit
eingetragen. Die schwarze Kurve würde dann erreicht werden, wenn mit steigender Anzahle
der Halbleitermodule auch die Oberfläche des Kühlkörpers und der Lüfter mit ansteigen
würde sowie sich die Halbleitermodule nicht gegenseitig beeinflussen würden. Tatsächlich
jedoch steigt der Kühlluftstrom weniger stark als die Anzahl der Halbleitermodule, und eine
gegenseitige Beeinflussung der Halbleitermodule findet statt.
2.3.3 Berechnung des erforderlichen Halbleiteraufwands
Mit den ermittelten Daten ist nun eine Auslegung des Demonstratorumrichters für
verschiedene Betriebspunkte möglich. Verglichen werden 3 Halbleitermodule 1700V/100A in
B6-Brückenschaltung mit folgender Chipbestückung:
A. Planare IGBT-Chips mit Standard Si Dioden
B. Planare IGBT Chips mit SiFast Dioden
C. Planare IGBT Chips mit SiC-Schottkydioden
Aus Gründen der Übersichtlichkeit werden hier noch einmal die Verlustkennlinien der zu
vergleichenden Leistungshalbleiter dargestellt:
68
Schaltverluste der Halbleitermodule (T=125°C)
18.00
Einschalten IGBT mit Si-Diode
16.00
E/[mWs]
14.00
Einschalten IGBT mit
SiFast-Diode
12.00
10.00
Ausschalten Si-Diode
8.00
Ausschalten SiFast-Diode
6.00
Ausschalten IGBT
4.00
2.00
Einschalten IGBT mit SiC-Diode
0.00
0.00
10.00
20.00
30.00
40.00
50.00
60.00
I/[A]
Abbildung 53: Vergleichende Darstellung der Halbleiterschaltverluste
Linearisierte Durchlasskennlinien, T = 125°C
60
SiFast-Diode
Si-Diode
50
IGBT
SiC-Diode
I/[A]
40
30
20
10
0
0
1
2
3
4
5
U/[V]
Abbildung 54: Vergleichende Darstellung der linearisierten Durchlasskennlinien
Für die Berechnung wurden folgende Randbedingungen zugrunde gelegt:
¾ Berechnet werden die Verluste für motorischen Betrieb (cosφ=0,9), generatorischen
Betrieb (cosφ=-0,9) und Ausgangsfrequenz null (cosφ=0).
¾ Der Umrichter wird dauerhaft mit Nennstrom betrieben. Zusätzlich erfährt er eine
kurzzeitige Überlast (3s) mit 150% Nennstrom [116], die jedoch so selten auftritt
(Wiederholfrequenz <300s), dass sie den dauerhaft wirksamen Effektivstrom nur
unwesentlich
beeinflusst.
Die
Temperaturabhängigkeit
der
unipolaren
Leistungshalbleiter wird berücksichtigt, bei den bipolaren Leistungshalbleitern wird sie
vernachlässigt.
69
6
¾ Bei motorischem und generatorischem Betrieb muss die Chiptemperatur eines jeden
Leistungshalbleiters unter 125°C liegen. Diese Temperatur ist der empfohlene
Arbeitsbereich der Leistungshalbleiter gemäß Datenblatt ([54], [56]).
¾ Bei Ausgangsfrequenz null muss die Chiptemperatur eines jeden Leistungshalbleiters
unter 150°C liegen. Diese Temperatur ist die spezifizierte maximale Chiptemperatur.
Da der Betrieb bei Ausgangsfrequenz null nicht als der dauerhaft relevante
Betriebspunkt für die Anwendung betrachtet wird, wird in diesem Fall eine erhöhte
Temperatur zugelassen.
¾ Die Temperatur des Kühlkörpers darf maximal 110°C betragen. Bei heißeren
Kühlkörpern ist in der Anwendung mit Problemen bei Bauteilen in der Nähe des
Kühlkörpers zu rechnen.
¾ Die Umgebungstemperatur beträgt 40°C. Dies ist heute eine gängige Randbedingung
für die Auslegung von Umrichtern [116].
¾ Der Vergleich wird für Schaltfrequenzen von 4kHz, 16kHz und 64kHz durchgeführt.
Als Ergebnis des Vergleichs wird die Anzahl der Halbleitermodule bewertet, die zur
Realisierung eines bestimmten effektiven Ausgangsstromes erforderlich sind.
4kHz
5
Anzahl Halbleitermodule
Si
4
SiFast
3
SiC
2
1
0
0
10
20
30
40
50
60
70
Ausgangsstrom/[A]
Abbildung 55: Erforderliche Halbleitermodule bei einer Schaltfrequenz von 4kHz
In Abbildung 55 ist die Anzahl der erforderlichen Halbleitermodule bei einer Schaltfrequenz
von 4kHz in Abhängigkeit des Umrichterausgangsstromes angegeben. Die gewählten
Stützstellen entsprechen einem realistischen Leistungsspektrum einer Umrichterreihe von
2,2kW bis 55kW.
Auch bereits bei der Schaltfrequenz von 4kHz sind Vorteile für die schaltverlustarmen
Halbleitervarianten zu erkennen. Allerdings ist der Vorteil nicht besonders groß, so dass bei
einem zu erwartenden höheren Preis der schnellen Si-Diode und besonders der SiCSchottkydiode dieser durch die Einsparung in der Halbleiterfläche möglicherweise nicht
kompensiert werden kann.
Selbstverständlich wird in der Realität immer eine ganzzahlige Anzahl von Halbleitermodulen
zum Einsatz kommen. In Abbildung 55 würde dies durch ein Aufrunden der jeweiligen
Lösung auf den nächsten ganzzahligen Wert erfolgen. Diese Diskretisierung wird in der
Anwendung dazu führen, dass bei einigen Ausgangsströmen kein Vorteil gegenüber einer
70
Standardlösung erzielt werden kann, der Übergang zur nächst höheren Anzahl jedoch bei
erhöhtem Umrichterausgangsstrom stattfindet und so bei einzelnen Ausgangsströmen
Vorteile entstehen. In einer konkreten Anwendung hängt ein solches Ergebnis jedoch stark
von der Verfügbarkeit der Halbleiterbauelemente in verschiedenen Stromtragfähigkeiten ab,
die je nach Hersteller und Betrachtungszeitraum variieren. Deshalb wird in dieser Arbeit der
grundsätzliche technische Vorteil durch die stetige Darstellung gezeigt und die
Diskretisierungseinflüsse bleiben unberücksichtigt.
16kHz
10
Si
Anzahl Halbleitermodule
9
SiFast
8
7
6
5
4
3
SiC
2
1
0
0
10
20
30
40
50
60
70
Ausgangsstrom/[A]
Abbildung 56: Erforderliche Halbleitermodule bei einer Schaltfrequenz von 16kHz
Betrachtet man die erforderlichen Halbleitermodule bei 16kHz Schaltfrequenz, so sind die
Vorteile der schnell schaltenden Lösungen weitaus offensichtlicher. In diesem Betriebspunkt
sind die Schaltverluste dominant. Mit der SiC-Schottkydiode kann nahezu das gesamte
Leistungsspektrum mit 3 Halbleitermodulen abgedeckt werden.
Bei der Auslegung des Umrichters wurden die Berechnungen bei einer Anzahl von 10
Halbleitermodulen abgebrochen. Diese zunächst willkürliche Grenze trägt dem Umstand
Rechnung, dass eine so große erforderliche Halbleiterfläche keine sinnvolle Lösung zur
Realisierung des erforderlichen Betriebspunktes darstellt.
Für die Halbleitermodule mit Si-Freilaufdioden aus Abbildung 56 bedeutet dies, dass
oberhalb einer bestimmten Leistung keine standardmäßige Realisierung möglich ist. Die
Ursache hierfür kann aus der Kennlinie der Schaltverluste in Abbildung 53 abgeleitet werden.
Bei der Betrachtung der Abschaltverluste der Si-Dioden ist zu beobachten, dass diese
Verluste jedoch mit steigendem Laststrom nur verhältnismäßig gering ansteigen.
Im Umkehrschluss bedeutet dies, dass auch bei sehr kleinem Laststrom bzw. geringer
Stromdichte noch nennenswerte Schaltverluste in der Diode auftreten. Physikalisch liegt dies
an
der
Tatsache,
dass
auch
bei
kleinem
Laststrom
bereits
eine
Ladungsträgerüberschwemmung der schwach dotierten Mittelschicht der Diode stattfindet.
Diese injizierten Ladungsträger müssen beim Schaltvorgang ausgeräumt werden. Dieser
Umstand trifft für alle bipolaren Bauelemente zu. Der IGBT ist hiervon ebenfalls betroffen, die
Auswirkung ist allerdings weniger stark als bei der Si-Diode, weil der IGBT für schnelles
Schalten und somit möglichst geringe Speicherladung optimiert ist.
71
Eine Erhöhung der Halbleiterfläche bei konstantem Laststrom bedeutet eine Reduzierung
der Stromdichte des einzelnen Halbleiterchips. Da die Speicherladung im Diodenchip jedoch
weitaus weniger stark als der Laststrom selbst zurückgeht, steigt die in der Summe aller
Diodenchips vorhandene Speicherladung mit der Halbleiterfläche stark an. Damit steigen
auch die Verluste der Gesamtanordnung an, wodurch die gewünschte Reduzierung der
Halbleitertemperatur durch Vergrößerung der Chipfläche und somit Verbesserung des
thermischen Widerstandes großteils zunichte gemacht wird.
Bei der Betrachtung der Ergebnisse ist zu berücksichtigen, dass die Anzahl der
erforderlichen Halbleitermodule auch ein Maß für die entstehende Verlustleistung ist. Somit
sinkt bei einer steigenden Anzahl erforderlicher Halbleitermodule der Wirkungsgrad des
Umrichters. Gleichzeitig steigt die Baugröße des Umrichters an, weil die hohe Anzahl von
Halbleitermodulen den Kühlkörper vergrößert. Die Baugröße des Kühlkörpers kann anhand
des Verlaufs des thermischen Widerstandes als Funktion der Anzahl der Halbleitermodule
aus Abbildung 52 abgeschätzt werden.
Wirkungsgrad 16kHz
100
SiC
98
Wirkungsgrad/[%]
96
94
SiFast
92
90
88
86
Si
84
82
80
0
10
20
30
40
50
60
Nennleistung/[kW]
Abbildung 57: Wirkungsgrad der Umrichtervarianten bei 16kHz Schaltfrequenz
Der Wirkungsgrad des Umrichters mit Si-Standarddiode nimmt mit steigender Leistung stark
ab. Diesem Umstand liegt die beschriebene Tatsache zugrunde, dass mit steigendem
Umrichterausgangsstrom die Leistungsfähigkeit des Kühlkörpers weniger stark als
proportional ansteigt (s. Abbildung 52). Um die anfallenden Verluste dennoch abführen zu
können, muss die Halbleiterfläche stark vergrößert werden und die Stromdichte in den
Halbleitern nimmt ab. Wie oben beschrieben, führt die vergrößerte Halbleiterfläche zu einer
erhöhten Speicherladung. Dieser Effekt macht sich vor allem in der Si-Freilaufdiode
bemerkbar, weil diese nicht für geringe Speicherladung optimiert ist. Qualitativ ist das
Verhalten auch bei der schnellen Si-Diode zu erkennen, allerdings in weit geringerem
Ausmaß. Der Umrichter mit der SiC-Schottkydiode zeigt den typischen steigenden
Wirkungsgrad mit steigender Leistung. Mit 98% ist der Wirkungsgrad akzeptabel,
insbesondere unter Berücksichtigung der hohen Schaltfrequenz.
72
64kHz
10
Si
Anzahl Halbleitermodule
9
SiFast
SiC
8
7
6
5
4
3
2
1
0
0
10
20
30
40
50
60
70
Ausgangsstrom/[A]
Abbildung 58: Erforderliche Halbleitermodule bei einer Schaltfrequenz von 64kHz
Betrachtet man eine Schaltfrequenz von 64kHz, so kann mit Si-Freilaufdioden auch die
kleinste Leistungsklasse nicht mehr realisiert werden. Rechnerisch wird kein stabiler Punkt
erreicht, weil durch eine Flächenvergrößerung der Halbleiter die Verluste stärker ansteigen
als der thermische Widerstand abnimmt.
Auch bei der SiC-Lösung steigt der Halbleiteraufwand an, die höchste Leistungsklasse kann
ebenfalls nicht mehr realisiert werden. Dies liegt in der Verwendung des Si-IGBTs, der trotz
high speed Ausführung noch immer eine Speicherladung und somit prinzipiell das gleiche
Problem wie die Si-Dioden besitzt. Bei sehr hohen Schaltfrequenzen wird der Punkt erreicht,
an dem unipolare Hochvoltbauelemente trotz ihrer hohen Durchlassverluste eine bessere
Performance zeigen.
2.4 Unipolarer Hochvoltschalter
In diesem Kapitel soll betrachtet werden, inwiefern ein unipolarer Hochvoltschalter als
Alternative zu der Kombination aus schnellem IGBT und SiC-Schottkydiode interessant ist.
Für Silizium sind unipolare Bauelemente mit einer Sperrspannung von 1500V und höher nur
in Einzelfällen mit geringer Stromtragfähigkeit verfügbar [107]. Diese hochsperrenden
MOSFETs sind für Schaltnetzteile mit hoher Frequenz und Leistungen <200W optimiert.
Das Halbleitermaterial SiC stellt jedoch auch hier in der Zukunft möglicherweise neuartige
Bauelemente zur Verfügung, die für Anwendungen im Frequenzumrichter von Interesse sind.
In der Literatur wird sowohl über SiC-MOSFETs als auch über SiC-JFETs berichtet. Für die
Anwendung im Frequenzumrichter erscheint nach der Literatur der JFET als die Struktur, die
zuerst für eine realistische Anwendung in Frage kommt, weil hier bereits über
Labormusterbauelemente mit einer Stromtragfähigkeit von mehreren Ampère für einen
Halbleiterchip berichtet wird ([38], [40], [75]).
73
2.4.1 Struktur des SiC-JFET
Die grundsätzliche Struktur eines solchen SiC-JFETs [75] wird im Folgenden kurz erläutert:
G
p+
n
S
lateraler Kanal
n+
p+
n-
n+
D
Abbildung 59: Struktur des SiC-JFET
Auf einem n+ -dotierten SiC-Wafer wird zunächst in einem ersten Epitaxieverfahren eine
niedrig dotierte n- -Schicht aufgewachsen. Die Dicke dieser schwach dotierten Schicht ist
proportional zur erforderlichen Sperrspannung des Bauelements. An der Oberfläche dieser n-Schicht wird anschließend eine p+ -Wanne sowie ein n+ -Sourcegebiet implantiert. Mit
einem zweiten Epitaxieschritt wird anschließend ein weiteres n-Gebiet aufgewachsen, das in
dem JFET als Kanalbereich verwendet wird und an der Oberfläche mit dem n+-Sourcegebiet
technologiebedingt kurzgeschlossen wird. Auf diesem zweiten n-Gebiet wird schließlich noch
ein p-Gategebiet implantiert, das derart ausgeführt wird, dass dieses p+-Gate einen Teil der
gegenüberliegenden p+-Wanne überdeckt und zwischen diesen beiden p+-Gebieten ein
lateraler n-Kanal eingeschlossen wird.
Wie aus Abbildung 59 zu erkennen ist, handelt es sich bei dem JFET um ein Bauelement,
das im nicht angesteuerten Zustand leitend ist. Von dem Drainanschluss an der Unterseite
des n+-Substrates bis zum Sourceanschluss auf der Bauelementoberseite existiert ein
durchgängiger Pfad mit n-Gebieten. Wird nun am Drainanschluss eine positive Spannung
gegenüber Source angelegt, so arbeiten die n-Gebiete als Widerstand, wobei die
Leitfähigkeit des jeweiligen Gebietes proportional zu seiner Dotierung ist. Die
Durchlasskennlinie des JFET ist rein ohmsch, da kein pn-Übergang im Durchlasspfad liegt,
der eine Schwellenspannung verursachen könnte.
Wie auch bei MOSFETs besitzt der JFET in Rückwärtsrichtung eine interne pn-Diode, die
dem Kanal parallel liegt. Die Schwellenspannung dieser Diode beträgt ca. 2,8V. Dieser Wert
ergibt sich aus den Materialeigenschaften von SiC [74].
Soll der JFET abgeschaltet werden, so muss an seinem Gateanschluss eine negative
Spannung gegenüber dem p+-Sourcegebiet angelegt werden. Bei einer solchen negativen
Spannung wird sich am p+n-Übergang zwischen p+-Gate und n-Kanal eine
Raumladungszone in das Kanalgebiet ausbreiten, die von freien Ladungsträgern nicht
passiert werden kann. Wird die negative Spannung am Gate so weit erhöht, dass die
74
Raumladungszone das p+-Wannengebiet erreicht, so ist der gesamte Kanalbereich
abgeschnürt und ein Stromfluss ist nicht mehr möglich. In diesem Betriebszustand ist der
JFET ausgeschaltet und kann Sperrspannung aufnehmen.
In der Literatur [38] wird berichtet, dass JFETs für eine Sperrspannung von 1200V mit einem
spezifischen On-Widerstand von 10 mΩcm2 bei Raumtemperatur realisiert worden sind. Da
der Durchlasswiderstand des Driftgebietes für unipolare Bauelemente quadratisch mit der
Sperrspannung steigt, ist für 1700V etwa mit dem doppelten spezifischen Driftwiderstand zu
rechnen, während der Kanal- und Substratwiderstand gleich bleibt. Ziel dieses Kapitels ist es
jedoch, das grundsätzliche Potenzial eines solchen unipolaren SiC-Schalters abzuschätzen.
Da der JFET eine noch recht neue Struktur darstellt, die bisher nur in
Labormusterstückzahlen produziert wurde, sind an dieser Stelle noch Verbesserungen zu
erwarten. Für die Bewertung des JFETs soll daher mit einem spezifischen On-Widerstand
von 15 mΩcm2 gerechnet werden.
2.4.2 Durchlassverhalten
Besonders interessant ist an dem JFET wie an allen unpolaren Schaltern, dass er bei
eingeschaltetem Kanal in der Lage ist, in beiden Richtungen ohne Schwellenspannung
Strom zu führen. Dies bedeutet, dass auf den Einsatz einer Freilaufdiode verzichtet werden
kann. Dadurch kann die Anzahl der Chips in einem Halbleitermodul halbiert werden. Dies
vereinfacht die Aufbautechnik in einem Halbleitermodul.
Die Durchlassverluste eines Bauelementes, das in beiden Richtungen Strom führt, können
durch die Addition von Gl. (37) (Durchlassverluste des IGBT) und Gl. (39) (Durchlassverluste
der Freilaufdiode) berechnet werden. Sie ergeben sich im allgemeinen Fall zu:
Pd = I C max U CE 0
⎛⎛ 1
⎜ ⎜⎜
⎜ 2π
⎝⎝
2
⎞ M cos φ ⎞ U CEN − U CE 0
⎟+
⎟⎟ +
I
C
max
⎟
I CN
8
⎠
⎠
⎛
⎜
•⎜
⎜
⎜
⎝
+ I C max U D 0
⎛⎛ 1
⎜ ⎜⎜
⎜ 2π
⎝⎝
2
⎞ M cos φ ⎞ U DN − U D 0
⎟+
⎟⎟ −
I
C
max
⎟
I CN
8
⎠
⎠
1 M cos φ ⎞⎟⎟
−
8
3π ⎟⎟⎠
⎛
⎜
•⎜
⎜
⎜
⎝
1 M cos φ ⎞⎟⎟
+
8
3π ⎟⎟⎠
(58)
Der unipolare JFET besitzt wie alle Feldeffekttransistoren keine Schwellenspannung, so
dass die Terme proportional zu UCE0 und UD0 aus Gl. (58) entfallen. Der ohmsche Widerstand
ist zudem unabhängig davon, in welcher Richtung der Strom durch den JFET fließt. Damit
gilt in Gl. (58):
U CEN − U CE 0 U DN − U D 0
=
= RdJFET
I CN
I CN
(59)
Für den Stromfluss von Source nach Drain (techn. Stromrichtung) ist die Annahme eines rein
ohmschen Durchlasswiderstandes nur unterhalb der Einsatzschwelle der parasitären pnDiode gültig. In Siliziumkarbid liegt diese Einsatzschwelle bei ca. 2.8V [5]. Bei dem
angenommenen spezifischen Durchlasswiderstand von 15 mΩcm2 wird dieser Wert ab einer
Stromdichte von 187A/cm2 erreicht. Ab dieser Stromdichte wird die Durchlassspannung in
Rückwärtsrichtung geringer als bei der Annahme der rein ohmschen Kennlinie. Für die
Auslegung wird dieser Umstand jedoch nicht berücksichtigt, weil im Fall rein motorischen
Betriebes (cosφ = 1) der Strom immer in Vorwärtsrichtung durch den JFET fließt und dieser
Betriebspunkt somit den auslegungsrelevanten worst case darstellt. Die Durchlassverluste
für den JFET vereinfachen sich somit zu:
75
PdJFET
R
⋅I
= dJFET C max
4
2
(60)
Gl. (60) ist unabhängig vom Lastwinkel cosφ. Die Auslegung der Chipfläche wird damit
unabhängig vom Lastwinkel am Umrichterausgang. Dies ermöglicht eine gleichmäßigere
Ausnutzung der Halbleiterfläche, da in Anwendungen mit aktivem Schalter und separater
Freilaufdiode der Schalter für motorischen und die Freilaufdiode für generatorischen Betrieb
ausgelegt werden muss. Betrachtet man nur die Durchlassverluste (Gl. (37) und Gl. (39)) so
trägt im motorischen Betrieb der aktive Schalter nahezu alle Verluste, während die
Freilaufdiode unbelastet ist. Im generatorischen Betrieb treten die Verluste nur in der
Freilaufdiode auf.
Durch den Ersatz der Schalter-Dioden-Kombination durch einen rückwärts leitfähigen
Schalter kann in Summe signifikant Halbleiterfläche eingespart werden. Nimmt man an, die
Durchlasskennlinien von aktivem Schalter, Freilaufdiode und rückwärts leitfähigem Schalter
seien identisch, so sind auch die erforderlichen Halbleiterflächen für alle drei Bauelemente
identisch. Da in der Schalter-Dioden-Kombination zwei Bauelemente benötigt werden und
mit dem rückwärts leitfähigen Schalter nur eines, könnte die gesamte Halbleiterfläche in
diesem Fall halbiert werden.
2.4.3 Nachbildung des Schaltverhaltens
Das dynamische Verhalten des JFET zeigt zum heutigen Zeitpunkt noch einige
Abweichungen von dem Verhalten eines idealen unipolaren Schalters [129]. Dies ist
insbesondere beim Abkommutieren des JFETs durch eine äußere Spannung der Fall.
DCP
D
n+
T1
n-
UZK
p+
n+
n
S
p+
G
ILast
D
G
T2
S
DCN
Abbildung 60: Kommutierung in einem JFET-Halbbrückenzweig
76
Abbildung 60 ist die Kommutierung in einer JFET-Halbbrücke gezeigt. Vor dem
Kommutierungsvorgang fließt der konstante Ausgangsstrom IA in Rückwärtsrichtung durch
den oberen JFET T1 zum positiven Zwischenkreispotenzial DCP (grüne Linie). T1 übernimmt
in diesem Betriebszustand somit die Funktion einer Freilaufdiode. Das Gate von T1 ist
eingeschaltet, so dass der Strom durch den n-Kanal von T1 fließen kann.
Nun soll der Ausgangsstrom auf des JFET T2 kommutiert werden. Vor dem
Kommutierungsvorgang ist das Gate von T2 ausgeschaltet, so dass T2 Sperrspannung
aufnehmen kann. Nach klassischem Kommutierungsverfahren muss nun zunächst das Gate
von T1 ausgeschaltet werden. Nach Verstreichen einer Wechselrichtersperrzeit, die
sicherstellt, dass T1 tatsächlich sicher abgeschaltet hat, kann nun T2 eingeschaltet werden
und den Laststrom übernehmen (rote Linie).
In dem Zeitraum der Wechselrichtersperrzeit, in dem beide Gates der JFETs ausgeschaltet
sind, muss der Laststrom weiter durch T1 fließen, da T2 noch sperrt. Der Kanal von T1 ist
jedoch bereits geschlossen, so dass der Laststrom durch die parasitäre pn-Diode von T1
fließen muss (blaue gestrichelte Linie). Indem diese SiC-pn-Diode aktiviert wird, werden in
das n- -Gebiet von T1 Ladungsträger injiziert. Beim anschließenden Einschalten von T2
müssen diese Ladungsträger wie bei jeder pn-Diode wieder ausgeräumt werden. Dadurch
entstehen nicht unerhebliche Abschaltverluste, weil der unipolare SiC-JFET beim
Kommutieren aus dem Freilaufzustand das Verhalten einer schnellen bipolaren Diode zeigt.
Diese Problematik ist in der Literatur von Si-MOSFETs bekannt. Als mögliche Lösung wird
dort ein Ansteuerverfahren vorgeschlagen, das als „synchroner Gleichrichterbetrieb“
bezeichnet wird [128]. In diesem Verfahren werden das Einschalten von T2 und das
Ausschalten von T1 derart koordiniert, dass der Laststrom vom Kanal des oberen FET in den
unteren FET kommutiert, ohne dass die parasitäre pn-Diode aktiviert wird und ohne dass ein
Brückenkurzschluss entsteht.
Dieses Verfahren erfordert eine hohe zeitliche Präzision der beiden Ansteuersignale, die
zudem noch auf unterschiedlichem Potenzial liegen. In der Literatur wurde diese Aufgabe
durch Hochvolt-IC’s gelöst, die sowohl den oberen als auch den unteren Schalter ansteuern
und die Potenzialtrennung intern via junction Isolation oder dielectric Isolation realisieren.
Diese Technologien für Hochvolt-IC’s sind heute jedoch nur für Halbleiterbauelemente bis
600V Sperrspannung verbreitet; einzelne Hochvolt-IC’s für 1200V Sperrspannung sind
ebenfalls bekannt [58]. Für 1700V Sperrspannung sind keine Hochvolt-IC’s verfügbar, so
dass die Lösung dieser Problematik weiterer Innovationsschritte bedarf [88].
Auf der anderen Seite befindet sich die JFET-Struktur noch stark in der Optimierungsphase,
so dass in der Zukunft deutliche Verbesserungen vor allem des dynamischen Verhaltens
erwartet werden können. Um das Potenzial des unipolaren Hochvoltschalters abschätzen zu
können, soll statt gemessener Schaltverluste eine einfache theoretische Nachbildung des
Schaltvorganges verwendet werden, das einem idealisierten Verhalten nahe kommt. Für
tiefer gehende Betrachtungen des Schaltverhaltens sei auf die Literatur ([15], [34])
verwiesen.
Zur Abschätzung der Schaltverluste des idealisierten Hochvoltschalters soll das Modell nach
Abbildung 61 verwendet werden. Der Einschaltvorgang findet im Zeitraum [t0; t2] statt.
77
U,I
UZK
ILast
t
t0
t1
t2
t3 t4 t5
Abbildung 61: Idealisiertes Schaltverhalten des unipolaren Hochvoltschalters
Zum Zeitpunkt t0 beginnt der einschaltende JFET mit dem Stromaufbau. Bis zum Erreichen
des Laststromes wird ein linearer Stromverlauf angenommen. Die Steilheit des
Stromanstieges wird theoretisch nur durch die Streuinduktivität des Kommutierungskreises
begrenzt
di U ZK
,
≤
dt
Ls
(61)
woraus sich bei 1000V Zwischenkreisspannung und einer Streuinduktivität von 100nH eine
maximale
Stromanstiegsgeschwindigkeit
von
10
kA
µs
errechnen
lässt.
In
realen
Ansteuerschaltungen wird die Stromanstiegsgeschwindigkeit jedoch durch eine Begrenzung
des Gatestroms eingestellt; für Umrichter mit Nennströmen <100A ist eine maximale
Stromanstiegsgeschwindigkeit von
di
kA
=1
zu beobachten. Die Verlustenergie im Intervall
dt
µs
[t0; t1] in Abhängigkeit vom Laststrom berechnet sich somit zu:
t1
E on1 = ∫ (U DS
t0
I last
di
2
dt
di I
di di
I D )dt = ∫ ((U ZK − Ls ) ⋅ t )dt =(U ZK − Ls ) Last
di
dt
dt dt
0
2
dt
(62)
Zum Zeitpunkt t1 hat der Strom im einschaltenden JFET den Laststrom erreicht. Der im
Freilauf arbeitende JFET wird verlustfrei abkommutiert, d.h. der synchrone
Gleichrichterbetrieb wird als ideal angenommen. Damit fallen in diesem im Freilauf
arbeitenden JFET keine Schaltverluste an. Der einschaltende JFET kann nun unmittelbar mit
78
dem Abbau seiner Sperrspannung beginnen; die Spannungsänderung wird nach den in
Kapitel 2.1.3 dargelegten Gründen mit
du
kV
= 15
gewählt.
dt
µs
Für die Schaltverluste in diesem Intervall [t1; t2] gilt:
U ZK − Ls
t2
du
dt
t1
0
E on 2 = ∫ (U DS I D )dt =
=
(U ZK − Ls
2
du
dt
∫
di
dt
(((U ZK − Ls
di
du
)−
⋅ t ) I Last )dt
dt
dt
(63)
di 2
)
dt I
Last
Mit dem Zeitpunkt t2 ist der Einschaltvorgang abgeschlossen. Nun folgt die Leitphase des
JFET, in der Verluste als Durchlassverluste auftreten. Zum Zeitpunkt t3 beginnt der
Abschaltvorgang des JFET. Dessen erste Phase ist gekennzeichnet durch einen linearen
Anstieg der Drainspannung des JFET. Parasitäre Kapazitäten am JFET und der Last sollen
in dieser Betrachtung vernachlässigt werden. Dann gilt für die Schaltverluste im Intervall [t3;
t4]:
t4
E off 1 = ∫ (U DS
t3
U ZK
du
dt
2
U
du
⋅ t ⋅ I Last )dt = ZK ⋅ I Last
I D )dt = ∫
du
0 dt
2
dt
(64)
Im Intervall [t4; t5] fällt der Laststrom bis auf 0. Die Fallzeit in diesem Intervall ist von internen
Eigenschaften des Schalters abhängig und nahezu unabhängig von der Höhe des
abzuschaltenden Stromes. Sie wird mit tf bezeichnet. Vereinfacht wird die
Stromänderungsgeschwindigkeit im Intervall [t4; t5] als linear angenommen. Aus
Messergebnissen kann diese Fallzeit mit 50ns angenommen werden. Für die Schaltverluste
im Intervall [t3; t4] gilt:
t5
tf
t4
0
E off 2 = ∫ (U DS I D )dt = ∫ ((U ZK + Ls
= (U ZK
I Last
I
) ( I Last − Last t )dt
tf
tf
(65)
I Last t f
I
+ Ls Last )
2
tf
Zum Zeitpunkt t5 ist der Ausschaltvorgang des JFET abgeschlossen. Einen Tailstrom wie
beim IGBT gibt es nicht, da es sich um ein unipolares Bauelement handelt.
79
2.4.4 Berechnung des Halbleiterbedarfs im Umrichterbetrieb
Mit Gl. (62) bis Gl. (65) können die Schaltverluste des idealisierten unipolaren
Hochvoltschalters in Abhängigkeit des Laststromes berechnet werden. Als
Schaltkreisparameter werden die gleichen Werte verwendet, die auch bei den
Verlustmessungen des IGBT mit Freilaufdiode ermittelt wurden:
¾ Zwischenkreisspannung
¾ Streuinduktivität
¾ Spannungssteilheit beim Ein- und Ausschalten
¾ Stromanstiegsgeschwindigkeit beim Einschalten
¾ Stromfallzeit beim Ausschalten
UZK = 1000V
Ls = 100nH
du
kV
= 15
dt
µs
di
kA
=1
dt
µs
tf = 50ns
Mit diesen Werten ergeben sich folgende Schaltverluste:
4
3.5
Ausschalten IGBT
3
Ausschalten JFET
2.5
E/[mWs]
Einschalten IGBT
mit SiC-Diode
Einschalten JFET
2
1.5
1
0.5
0
0
10
20
30
40
50
60
Strom/[A]
Abbildung 62: Berechnete Schaltverluste eines unipolaren Hochvoltschalters
Die zu erwartenden Schaltverluste des JFET sind um etwa 20% geringer als die
gemessenen bei dem schnellen IGBT mit der SiC-Schottkydiode. Die Ursache für diesen
Unterschied liegt zum überwiegenden Teil in den Tailverlusten und der dynamischen
Einschaltspannung des IGBT, da die Steilheiten für Strom und Spannung identisch
angenommen wurden.
Im Umkehrschluss ist bei der thermischen Auslegung zu erwarten, dass die Schaltfrequenz
eines Umrichters mit JFETs um maximal 20% erhöht werden kann, wobei hierbei
Durchlassverluste und thermischer Widerstand noch nicht betrachtet sind. Da die Motivation
für einen Umrichter mit JFETs jedoch der Wunsch nach deutlich höheren Schaltfrequenzen
ist, wird es erforderlich sein, für einen JFET-Umrichter die Schaltsteilheiten deutlich zu
erhöhen.
80
4
3.5
Ausschalten IGBT
3
Ausschalten JFET
2.5
E/[mWs]
Einschalten IGBT
mit SiC-Diode
Einschalten JFET
2
1.5
1
Ausschalten JFET fast
0.5
Einschalten JFET fast
0
0
10
20
30
40
50
60
Strom/[A]
Abbildung 63: Schaltverluste des JFET bei erhöhter Schaltgeschwindigkeit
Bei der Berechnung der mit „JFET fast“ bezeichneten Schaltverlustenergien wurden die
Spannungsanstiegsgeschwindigkeit und die Stromanstiegsgeschwindigkeit um den Faktor
10 erhöht sowie die Stromfallzeit um den Faktor 10 reduziert. In dieser Lösung ist eine
nahezu proportionale Absenkung der Schaltverluste möglich, weil in dem Modell für die
Schaltverluste nahezu alle Terme linear von der Schaltgeschwindigkeit abhängen. Allerdings
ist zu berücksichtigen, dass in diesem Fall eine Spannungssteilheit von 150
kV
erreicht wird,
µs
die an allen Bauteilen auftritt, die die Potenzialtrennung für Stromversorgung und
Ansteuerbefehle der oberen JFETs gewährleisten. Ein gesamter Schaltvorgang besitzt eine
Dauer von ca. 10ns. Dies ist deutlich schneller als heute in Frequenzumrichtern realisiert und
kann somit als Extremabschätzung verwendet werden, welches Potenzial ein unipolarer SiCHochvoltschalter in einer praktischen Anwendung haben könnte.
Die angenommenen Durchlassverluste von 15mΩcm2 für den unipolaren Hochvoltschalter
werden aus Gründen der Vergleichbarkeit ebenfalls in einem Diagramm mit der SiCSchottkydiode und dem schnellen IGBT dargestellt:
Linearisierte Durchlasskennlinien, T = 125°C
60
SiC-Schottky-Diode
IGBT
50
SiC-JFET
I/[A]
40
30
20
10
0
0
1
2
3
4
5
6
U/[V]
Abbildung 64: Linearisierte Durchlasskennlien für SiC-JFET, SiC-Schottkydiode und Planaren
Si IGBT
81
Aus Gründen der Vergleichbarkeit wurde bei der Berechnung der Durchlasskennlinie der
JFET mit identischer Halbleiterfläche wie die SiC-Schottkydiode zu Grunde gelegt. Im
vorliegenden Fall beträgt die SiC-Fläche 12,6mm2. Durch die identischen Bezugsflächen ist
sichergestellt, dass Ergebnisunterschiede zwischen den benötigten Flächen von JFET und
Schottkydiode in erster Näherung ein Maß für die Materialkosten darstellt, sofern man davon
ausgeht, dass die SiC-Fläche sowohl bei einem JFET-Modul als auch bei einem Modul mit
Si-IGBTs und SiC-Schottkydioden den Modulpreis dominiert. Damit sind die berechneten
erforderlichen Halbleiterflächen der einzelnen Chipvarianten in erster Näherung proportional
zum jeweiligen Aufwand für die Bauelemente. Bei dieser Betrachtung werden zwei Effekte
vernachlässigt:
¾ die beim JFET im Vergleich zur Schottkydiode aufwändigere SiC-Technologie
¾ die erforderliche Si-Halbleiterfläche bei der Lösung mit IGBT und Schottkydiode
Diese Effekte besitzen bzgl. des erforderlichen Halbleiteraufwandes gegenläufigen Charakter
und kompensieren sich zumindest teilweise, so dass die Annahme eines identischen
Modulpreises gerechtfertigt ist.
An den Kennlinien in Abbildung 64 ist auffällig, dass der Widerstand des JFETs höher ist als
der On-Widerstand der Schottkydiode. Da die Dicke der schwach dotierten Epitaxieschicht
zur Aufnahme der Sperrspannung bei beiden Bauteilen sehr ähnlich ist, resultiert dieser
Unterschied zum überwiegenden Teil in dem Durchlasswiderstand des Kanals in Abbildung
59, der mit der zweiten Epitaxieschicht gebildet wird [75].
Mit den Schaltverlusten und den angenommenen Durchlassverlusten kann nun analog zur
Auslegung mit IGBT und Freilaufdiode berechnet werden, welche Chipfläche des unipolaren
Hochvoltschalters zur Realisierung der Umrichterreihe erforderlich ist.
16kHz
6
JFET
Anzahl Halbleitermodule
5
JFET
ultrafast
4
3
IGBT mit SiCSchottkydiode
2
1
0
0
10
20
30
40
50
60
70
Ausgangsstrom/[A]
Abbildung 65:Anzahl der erforderlichen Halbleitermodule mit unipolaren Hochvoltschaltern bei
16kHz
Bei einer Schaltfrequenz von 16kHz ist mit dem unipolaren Hochvoltschalter eine um 50%
größere SiC-Fläche erforderlich als sich bei der Berechnung mit der SiC-Schottkydiode als
Freilaufdiode zu dem schnellen IGBT ergibt. Mit dem schnellen Schalten können ca. 20% der
erforderlichen Halbleiterfläche eingespart werden, aber der Bedarf liegt immer noch über der
erforderlichen Fläche der Schottkydiode.
82
Ursache hierfür sind die erhöhten Durchlassverluste des unipolaren Hochvoltschalters.
Betrachtet man die Schaltverluste des JFET ultrafast vereinfacht als vernachlässigbar, so
erklären die Durchlassverluste den Unterschied zwischen dem JFET ultrafast und der SiCSchottkydiode.
Zusätzlich erfährt der mit standardmäßiger Schaltgeschwindigkeit betriebene JFET noch
Schaltverluste, die in der Schottkydiode nicht angefallen sind, sondern von dem
großflächigen IGBT übernommen wurden. Um diese Schaltverluste abzuführen, benötigt der
JFET zusätzliche Fläche zur Reduzierung seines thermischen Widerstandes.
Wirkungsgrad 16kHz
100
99.6
Wirkungsgrad/[%]
99.2
JFET ultrafast
98.8
JFET
98.4
98
IGBT mit SiCSchottkydiode
97.6
97.2
96.8
96.4
96
0
10
20
30
40
50
60
Nennleistung/[kW]
Abbildung 66: Wirkungsgrad des Umrichters mit unipolarem Hochvoltschalter
Betrachtet man die Verluste und den Wirkungsgrad, so ist zu erkennen, dass der unipolare
Hochvoltschalter gegenüber der Kombination aus IGBT und SiC-Schottkydiode Vorteile
bietet. Mit der schnellen Lösung kann der Wirkungsgrad um 0,7% gesteigert werden.
Allerdings stellt sich die Frage, ob dieser Vorteil den großflächigeren Einsatz der teueren
SiC-Bauteile rechtfertigt.
Überträgt man das Verhalten der Bauelemente auf eine Schaltfrequenz von 64kHz, so
werden die Vorteile des unipolaren Hochvoltschalters sichtbar.
64kHz
10
JFET
Anzahl Halbleitermodule
9
8
7
IGBT mit SiCSchottkydiode
6
5
JFET
ultrafast
4
3
2
1
0
0
10
20
30
40
50
60
70
Ausgangsstrom/[A]
Abbildung 67: Anzahl der erforderlichen Halbleitermodule mit unipolaren Hochvoltschaltern bei
64kHz
83
Mit dem schnellen Schalten steigt der Bedarf an zusätzlicher Halbleiterfläche kaum an,
während bei konventioneller Schaltgeschwindigkeit nahezu eine Verdopplung der
Halbleiterfläche erforderlich ist. Gegenüber dem Halbleitermodul mit IGBT und SiCFreilaufdiode kann die Fläche bei dem schnellen Schalten ebenfalls reduziert werden.
Allerdings ist bei einer Schaltfrequenz von 64kHz die SiC-Schottkydiode in dem
Halbleitermodul nicht mehr optimal ausgenutzt, weil die Verluste des IGBT den Modulbedarf
bestimmen.
Wirkungsgrad 64kHz
100
99.4
JFET ultrafast
Wirkungsgrad/[%]
98.8
98.2
97.6
JFET
97
96.4
IGBT mit SiCSchottkydiode
95.8
95.2
94.6
94
0
10
20
30
40
50
60
Nennleistung/[kW]
Abbildung 68: Wirkungsgrad des Umrichters mit unipolarem Hochvoltschalter bei 64kHz
Schaltfrequenz
Bezüglich des Wirkungsgrades zeigt der unipolare Halbleiterschalter allerdings deutliche
Vorteile gegenüber der Variante aus IGBT und Schottkydiode. Dies wird durch die
vergleichsweise hohen Schaltverluste des IGBT verursacht. Der Wirkungsgrad bei dem sehr
schnell schaltenden JFET mit 64kHz Schaltfrequenz ist im Vergleich zu dem Ergebnis bei
16kHz nur minimal verschlechtert.
Für einen echten Aufwandsvergleich zwischen unipolarem Hochvoltschalter und der
Kombination aus IGBT und SiC-Schottkydiode müsste der Chipsatz von IGBT und
Schottkydiode für jede Frequenz optimiert werden. Da die Schaltverluste des IGBT (s.
Abbildung 53) analog zu den Schaltverlusten der Si-Freilaufdioden – wenn auch in
geringerem Maße - bei kleinem Strom nicht proportional sinken, wird bei sehr hohen
Schaltfrequenzen die erforderliche IGBT-Fläche überproportional ansteigen und schließlich
einen Punkt erreichen, an dem eine Lösung nicht mehr möglich ist.
Auf derartige Vergleiche soll an dieser Stelle verzichtet werden, weil sie eine detaillierte
Betrachtung jedes individuellen Einzelfalles erfordern, der durch eine Anwendung
vorgegeben wird. Als generelle Abschätzung für die erforderliche JFET-Fläche im Bezug auf
die Schottkydiodenfläche kann ein Vergleich der Verluste von JFET und SiC-Schottkydiode
verwendet werden. Für eine Grenzbetrachtung können die Schaltverluste des unipolaren
Hochvoltschalters zu null angenommen werden, indem sein Schaltverhalten als ideal
betrachtet wird. Dann ergibt sich die minimal erforderliche Halbleiterfläche des unipolaren
Hochvoltschalters unabhängig von der Schaltfrequenz allein aus den Durchlassverlusten.
Die Durchlassverluste der Schottkydiode müssen im generatorischen Betriebspunkt
berechnet werden, da sie dort maximal sind.
84
100
1.8
90
1.6
80
1.4
70
1.2
60
1
50
0.8
40
0.6
30
0.4
20
0.2
10
0
Temperaturhub JFET/[K]
PJFET/PSBD
2
0
0
10
20
30
40
50
In/[A]
Abbildung 69: Verhältnis der Durchlassverluste von JFET und Schottkydiode und
Temperaturhub des JFET bei idealem Schaltverhalten und identischer Halbleiterfläche
Unter diesen Randbedingungen ergibt sich auf Basis der Durchlasskennlinien von SiC-JFET
und SiC-Schottkydioden aus Abbildung 64 die rote Kennlinie für die bezogenen Verluste des
JFET. Die fehlende Schwellenspannung des unipolaren Hochvoltschalters macht sich bei
kleinem Strom stark bemerkbar, so dass bis ca. 9A der JFET trotz höherem
Durchlasswiderstand geringere Verluste verursacht. Bei höherem Strom kehrt sich dieses
Verhältnis um.
Die blaue Kurve in Abbildung 69 zeigt die Temperaturerhöhung des JFET, die bei dem
jeweiligen Laststrom entsteht. Sie dient zur Abschätzung eines realistischen
Arbeitsbereiches. Heutige Leistungshalbleiter sind mit einer maximalen Junctiontemperatur
von 125°C spezifiziert. Nimmt man eine Kühlkörpertemperatur von 100°C unter dem
Halbleitermodul an, so ergibt sich ein zulässiger Temperaturhub von 25°C für den Chip.
Betrachtet man dies als typischen Arbeitsbereich, so kann aus Abbildung 69 die Aussage
abgeleitet werden, dass bei der gewählten Fläche des JFET von 12,6mm2 maximal ein
Effektivstrom von 27A geführt werden kann. Bei diesem Strom sind die Verluste des JFET
allerdings bereits um ca. 50% höher als die Verluste der Schottkydiode.
Zusammenfassend kann festgehalten werden, dass für Anwendungen mit hoher
Schaltfrequenz (z.B. über 50kHz) der JFET trotz der höheren Durchlassverluste ein sehr
interessantes Potenzial besitzt. Allerdings ist es dann für die Ausnutzung der Vorteile
erforderlich, die Schaltgeschwindigkeit gegenüber dem heutigen Stand der Technik um eine
Größenordnung zu erhöhen. Für Schaltfrequenzen bis 16kHz wird ein Vorteil gegenüber der
Schottkydiode selbst bei idealem Schaltverhalten nur bei geringen Stromdichten unter
90A/cm2 sichtbar. Bereits heute wird mit Si-Bauelementen diese Stromdichte erreicht, mit
SiC könnte sie nur für Sonderanwendungen interessant sein, in denen zur Vermeidung von
Verlusten die Bereitschaft für hohe Materialkosten existiert.
2.5 Moduldesign
Für die favorisierte Lösung mit schnellem Si-IGBT und SiC-Freilaufdiode ist ein geeignetes
Halbleitermodul zu entwerfen. In dem betrachteten Leistungsbereich von 2,2kW bis 55kW
können Umrichter realisiert werden, die ihre gesamte Stromführung auf einer mehrlagigen
Leiterplatte realisieren und auf Kupferschienen vollständig verzichten. Diese Aufbautechnik
ermöglicht eine kostengünstige und platzoptimierte Lösung, da auf einer Leiterplatte die
85
erforderlichen Luft- und Kriechstrecken geringer ausgelegt werden können als bei der
Verwendung einer Kupferverschienung.
Demzufolge entsteht auch an das Halbleitermodul die Forderung, direkt über Löt- oder
Druckkontakte die Leiterplatte zu kontaktieren. Derartige Halbleitermodule sind
standardmäßig z.B. seitens Fa. Infineon verfügbar. Allerdings sind die Luft- und
Kriechstrecken bei diesen Halbleitermodulen nur unwesentlich größer als der minimale, von
Normen geforderte Abstand. Für einen Einsatz z.B. in verschmutzter Umgebung ist dies
nicht optimal.
Deshalb soll in diesem Kapitel ein optimiertes Modul erarbeitet werden. Dieses Modul soll
zum einen möglichst große Luft- und Kriechstrecken realisieren und zum anderen einen
möglichst niederinduktiven Kommutierungskreis sowie eine möglichst geringe Einkopplung
von Lastsignalen in die Ansteuersignale gewährleisten. Als Basis wird hierbei ein Modul mit
Lötpins gewählt, weil mit dieser Technologie der erforderliche Leitungsbereich sicher
abgedeckt werden kann und darüber hinaus in dieser Technologie mit verhältnismäßig
geringem Aufwand neuartige Pinanordnungen realisiert werden können.
Lastseite
U
V
W
NTC
DC+
DC+
DC-
DC-
GU1
GL1
GU2
GL2
GU3
GL3
Ansteuerseite
Abbildung 70: Modul mit Pinlayout nach Stand der Technik
In Abbildung 70 ist ein standardmäßiges Halbleitermodul [55] mit einer B6-Brücke für einen
dreiphasigen Wechselrichter mit einem Temperatursensor dargestellt. Der Bereich der
Anschlusspins entspricht einer Fläche am Modulrand, zusätzlich ist die interne
Halbleiterschaltung mit ihren Anschlussleitungen an die Pins eingezeichnet. An der unteren
Längsseite des Moduls sind alle Anschlüsse für die Steuerbefehle angeordnet. An der
gegenüberliegenden Längsseite befinden sich die Anschlüsse für die AC-Lastabgänge des
Wechselrichters.
An
den
beiden
kurzen
Seiten
befinden
sich
die
Gleichspannungsanschlüsse.
Bewertet man diese Ausführungsform nach der Störfestigkeit, mit der Einkopplungen in die
Ansteuerkreise vermieden werden, so fällt auf, dass induktive Einkopplungen von der
86
Lastseite auf die Ansteuerseite durch den großen Abstand zwischen Lastseite und
Ansteuerseite gut unterdrückt werden. Allerdings müssen auf der Ansteuerseite sehr viele
Ansteuerungen untergebracht werden. Dies hat zur Folge, dass die Ansteuerschaltungen
nicht ideal nahe an den Modulpins angeordnet werden können. Damit sind längere
Zuleitungen von den Ansteuerschaltungen zu den Modulpins erforderlich, die für induktive
Einkopplungen anfällig sind.
Betrachtet man kapazitive Störkopplungen, so erweist sich die Ansteuerseite als sehr
problematisch. Durch die Vielzahl der Ansteuerungen, die auf einer Modulseite platziert
werden müssen, werden Kreuzungen von Leitungen unterschiedlicher und zudem schnell
veränderlicher Spannungsniveaus in verschiedenen Lagen der Leiterplatte nur schwer zu
umgehen sein. Diese Kreuzungen stellen eine große Einkopplungsquelle kapazitiver
Störströme dar, da der Abstand der Signale in zwei benachbarten Leiterplattenlagen nur
0,5mm beträgt und somit eine große Koppelkapazität zwischen den Leiterbahnen existiert.
In Abbildung 70 sind Pins mit jeweils gleichem bzw. nur geringfügig unterschiedlichem
Potenzial jeweils mit identischer Farbe dargestellt. Dies bedeutet, dass zwischen allen
Bereichen unterschiedlicher Farbe möglichst hohe Luft- und Kriechstrecken eingehalten
werden sollen, um ein robustes Verhalten des Umrichters bzgl. Spannungsüberschlags,
insbesondere beim Betrieb in verschmutzter Umgebung, zu erreichen.
Bei dem Modul aus Abbildung 70 existieren 13 Bereiche, an denen unterschiedliche
Potenziale mittels Luft- und Kriechstrecken voneinander getrennt werden müssen. Diese
hohe Anzahl an erforderlichen Luft- und Kriechstrecken beschränkt die mögliche
Ausdehnung jeder einzelnen Luft- und Kriechstrecke. Dieses Problem verschärft sich mit
zunehmender Anschlussspannung des Umrichters; bei dem betrachteten System mit einer
Anschlussspannung von 690V wirken sich die Luft- und Kriechstrecken gravierend aus.
U, GU1
V, GU2
W,GU3
DC+
DC+
DC-
GL1
GL2
NTC
GL3
DC-
Abbildung 71: Modul mit optimierter Pinanordnung
Zur Verbesserung wurde eine Ausgestaltung des Halbleitermoduls nach Abbildung 71
realisiert [54]. Bei dieser Lösung sind die Last- und Steuersignale eines Spannungsniveaus
örtlich zusammengefasst. Lediglich der positive Zwischenkreisanschluss bleibt getrennt, um
einen symmetrischen Anschluss zu gewährleisten. Die Anzahl erforderlicher Potenzialgräben
kann bei dieser Lösung von vormals 13 auf 6 reduziert werden. Dies ermöglicht einen
87
großen Abstand zwischen den einzelnen Potenzialinseln, wodurch die Durchschlagfestigkeit
bei Spannungsüberschlägen unter Verschmutzung verbessert wird. Kapazitive
Störeinkopplung wird ebenfalls durch die großen Abstände minimiert.
Das Problem der induktiven Störeinstrahlung ist zu berücksichtigen, da nun örtlich nahe an
den Ansteuerschaltungen auch der hohe Laststrom fließt. Die induktive Einkopplung kann
minimiert werden, indem die Laststrombahnen nicht direkt unterhalb der
Ansteuerschaltungen geführt werden. Eine Lösung ist im Detail für jede einzelne
Entflechtung zu finden, grundsätzlich wirkt sich jedoch positiv aus, dass aufgrund der lokal
einheitlichen Spannungsniveaus bei der Trennung von Last- und Steuerkreisen keine hohen
Abstände wegen Spannungsfestigkeit eingehalten werden müssen.
Ein weiteres Ziel bei dem Moduldesign besteht darin, die Anzahl erforderlicher Pins auf ein
Minimum zu begrenzen. Da sich Pins in einem vorgegebenen Rastermaß am Modul
befinden, verbessert eine geringe Anzahl von Pins wiederum die Möglichkeit,
Spannungsabstände zu maximieren. Darüber hinaus stört jeder Pin bei der Entflechtung,
weil er als Durchkontaktierung die Nutzung der Innenlagen einer Leiterplatte einschränkt.
In Modulen nach Stand der Technik werden als Steueranschlüsse pro IGBT ein Gatepin und
ein Hilfsemitterpin benötigt. Der Hilfsemitter befindet sich virtuell auf dem Potenzial des
Hauptemitters und unterscheidet sich von diesem nur während kurzer Zeiten während der
Kommutierung. Er ist erforderlich, um eine Rückkopplung induktiver Spannungsabfälle an
parasitären Induktivitäten aus dem Lastkreis auf den Steuerkreis zu verhindern. Zur
Erklärung dieses Sachverhaltes kann ein Ersatzschaltbild für eine Modulphase verwendet
werden, in dem alle parasitären Induktivitäten eingetragen sind:
Modulpin
DC positiv
LRB
LCU
Modulpin
Gate upper
T1
LRB
CZK
LCU
LCU
LSB
Driver upper
LRB
Modulpin
Hilfsemitter
upper
D1
LSB
LSB
LCU
LCU
LRB
LCU
LSB
Modulpin
AC
LCU
Modulpin
Gate lower
LCU
T2
LRB
LCU
LSB
LRB
LCU
LSB
LSB
D2
LCU
LSB
Driver lower
Modulpin
Hilfsemitter
lower
LCU
LRB
Modulpin
DC negativ
Abbildung 72: Ersatzschaltbild eines Standardmoduls mit parasitären Induktivitäten
Abbildung 72 zeigt die Phase eines Wechselrichters mit dem zugehörigen Zwischenkreis und
allen standardmäßigen Modulanschlusspins, das Halbleitermodul ist schematisch mit grün
skizziert. Die blau gezeichneten Elemente liegen in Kommutierungskreisen, die an einem
Bespiel im Folgenden kurz erläutert werden sollen. Hierzu stelle man sich vor, dass vor der
Kommutierung der Laststrom am AC-Anschluss durch die Diode D1 in den
Zwischenkreiskondensator und von dort in eine benachbarte Phase fließt. In der
betrachteten Phase soll der Strom von D1 auf T2 kommutiert werden.
88
Durch Einschalten von T2 fließt ein Kommutierungsstrom vom Zwischenkreiskondensator in
Rückwärtsrichtung durch D1 und durch T2. Sobald dieser Strom die Höhe des Laststromes
erreicht, verlöscht D1 und der Strom ist auf T2 kommutiert.
Nach dem Einschalten von T2 fließt der Kommutierungsstrom über dem Modulpin „DC+“ in
das Modul. Dort befindet sich als Verbindungselement vom Pin auf das Substrat ein
Bonddraht, dessen Induktivität mit LRB nachgebildet wird. Dieser Bonddraht wird als
Rahmenbonddraht bezeichnet, weil alle Pins in einem Kunststoffrahmen eingesteckt oder
eingespritzt sind. Auf dem Substrat fließt der Strom über eine Kupferbahn zu dem
Halbleiterchip D1. Die Induktivität dieser Kupferbahn wird mit LCU modelliert. Der Diodenchip
ist mit seiner Kathodenseite auf die Kupfermetallisierung aufgelötet, so dass an dieser Stelle
keine zusätzliche Induktivität entsteht.
Von der Anode der Diode fließt der Strom über einen weiteren Bonddraht auf eine
Kupferbahn. Dieser Bondraht wird als Substratbond bezeichnet, weil er Elemente verbindet,
die sich alle auf einem Keramiksubstrat befinden. Seine Induktivität wird LSB bezeichnet.
Nun hängt es von der tatsächlichen Ausgestaltung eines Halbleitermoduls ab, ob der Strom
noch über weitere Bonddrähte oder direkt zu dem unteren IGBT fließt. In Abbildung 72 sind
zwei weitere Substratbonddrähte gezeichnet, von denen einer im gemeinsamen Pfad von
IGBT und Diode liegt. An dem untern IGBT T2 fließt der Strom wieder zunächst über eine
Kupferbahn und anschließend durch den Chip T2. An den Emitter von T2 schließt sich ein
weiterer Substratbonddraht, eine Kupferbahn und schließlich der Rahmenbonddraht an,
bevor der Stromkreis zum Zwischenkreiskondensator geschlossen ist.
Der Ansteuerkreis für einen IGBT erstreckt sich von der Ansteuerschaltung (Driver upper
bzw. Driver lower) über einen Rahmenbonddraht, eine Kupferbahn und mindestens einen
Substratbonddraht zur Gatemetallisierung des IGBT-Chips. Im IGBT fließt der Strom durch
die Gate-Emitter-Kapazität zur Emittermetallisierung. Über die Emitterbonddrähte fließt der
Strom über Kupferbahnen und einen Rahmenbonddraht zum Hilfsemitteranschluss des
Moduls. Über eine Leiterbahn auf der PCB wird der Ansteuerkreis zur Ansteuerschaltung
geschlossen.
Die rot eingezeichneten Elemente liegen sowohl im Last- als auch im Steuerkreis. Bei hohen
Stromänderungsgeschwindigkeiten im Lastkreis koppeln diese Elemente einen
Spannungsabfall in den Ansteuerungskreis ein. Dieses Phänomen ist unter dem Begriff
induktive Gegenkopplung [101] bekannt und bis zu einem gewissen Grad erwünscht, da sie
die Ansteuerung des IGBT erleichtert.
Laststrom
LCU
LRB
LCU
LSB
UCGE
USteuer
LRB
T2
ULSB
LSB
LCU
Laststrom
Abbildung 73: Induktive Gegenkopplung
89
Betrachtet man beispielsweise den Ausschaltvorgang des IGBT, so nimmt der Laststrom in
dem IGBT ab. Die Spannung ULSB ist in diesem Fall negativ. Damit addiert sie sich zu der
Ansteuerspannung und erhöht die effektive Gatespannung UCGE am IGBT Chip. Dieser wird
somit während des Ausschaltvorganges wieder leicht aufgesteuert und reduziert damit seine
Schaltgeschwindigkeit. Diese Reduzierung der Schaltgeschwindigkeit bewirkt eine
Reduzierung der Überspannung am IGBT und schützt somit den Chip. Diese induktive
Gegenspannung wird passiv erzeugt und reagiert damit ohne Zeitverzug. Aktive
Schutzmaßnahmen von der Ansteuerschaltung können nur deutlich langsamer wirksam
werden.
In analoger Weise wird die Schaltgeschwindigkeit auch beim Einschalten reduziert, was die
abschaltende Diode vor Überspannungen schützt. Die induzierte Überspannung wirkt so
immer ihrer Ursache, der Schaltgeschwindigkeit, entgegen.
Zu hohe Induktivitäten können allerdings dazu führen, dass die Schaltgeschwindigkeit zu
stark abgesenkt wird und ein sicheres Schalten gefährdet wird, möglicherweise können
Schwingungen beim Schaltvorgang auftreten. Die Wahl der wirksamen Kopplungsinduktivität
ist somit beim Moduldesign eine wichtige Größe, die vom Modulhersteller eingestellt werden
muss. Bestimmt wird sie durch den Ort auf der DCB, an dem der Hilfsemitter auf dem
Substrat platziert wird. Wesentliche Einflussgröße ist die Länge der Emitterbonddrähte
zwischen Chipemitter und dem Hilfsemitterabgriff.
In Abbildung 72 sind drei Arten von Induktivitäten eingezeichnet: die Induktivität von
Kupferbahnen auf der DCB, die Induktivität der Substratbonddrähte und die Induktivität der
Rahmenbonddrähte. Die Induktivität der Kupferbahnen ist sehr klein, da die DCB auf der
Rückseite der Keramik eine durchgehende Kupfermetallisierung aufweist. In dieser
Kupfermetallisierung können somit ungehindert Ausgleichsströme fließen, die den Strömen
in den Kupferbahnen auf der Oberseite der DCB entgegengerichtet sind und deren
Magnetfeld somit kompensieren.
Die Induktivität der Substratbonddrähte ist wesentlich größer. Zwar können auch deren
Ströme auf der Rückseite der DCB kompensierende Ströme hervorrufen, doch der Abstand
der Bonddrähte ist im Vergleich zur Dicke der Keramik wesentlich größer, so dass eine
Kompensation nur in geringem Maße stattfindet.
Die Induktivität der Rahmenbonddrähte kann überhaupt nicht kompensiert werden, da keine
leitende Fläche existiert, auf der Ausgleichsströme fließen könnten. Zudem besitzen die
Rahmenbonddrähte i.a. eine verhältnismäßig große Länge, da sie vom Rahmen die DCB
erreichen müssen. Die Induktivität der Rahmenbonddrähte ist somit am größten.
Wie eingangs erwähnt, stellt die mögliche Reduzierung von Pins ein attraktives Ziel dar.
Betrachtet man die Hilfsemitterpins in Abbildung 72, so stellt man fest, dass sie in erster
Näherung für die Funktion nicht erforderlich sind, da auf gleichem Potenzial entsprechende
Lastanschlüsse vorhanden sind.
In Abbildung 74 ist ein Modul gezeichnet, das keine Hilfsemitteranschlüsse besitzt.
Betrachtet man die Koppelelemente zwischen Lastkreis und Steuerkreis, so ist zu erkennen,
dass am unteren IGBT T2 die wirksame Kopplungsinduktivität deutlich vergrößert wird, weil
nun ein Rahmenbonddraht als Kopplungselement wirkt. Eine solche Lösung könnte nur für
sehr kleine Wechselrichterleistung verwendet werden, da bei kleiner Leistung der Laststrom
und somit auch dessen Änderung gering sind. Bei mittlerer und hoher Leistung wäre die
Steuerbarkeit eines derartigen Moduls jedoch stark eingeschränkt.
90
Modulpin
DC positiv
LRB
LCU
Modulpin
Gate upper
LRB
CZK
LCU
T1
LCU
LSB
Driver upper
D1
LSB
LSB
LCU
LCU
LRB
LSB
Modulpin
AC und
Hilfsemitter
upper
LCU
Modulpin
Gate lower
LCU
T2
LRB
LCU
LSB
D2
LSB
LSB
LCU
LSB
Driver lower
LCU
LRB
Modulpin
DC negativ
und
Hilfsemitter
lower
Abbildung 74: Modul ohne Hilfsemitteranschlüsse
Betrachtet man den oberen IGBT T1, so liegt nun der Rahmenbonddraht des ACLastanschlusses im Steuerkreis. Dieser Rahmenbonddraht liegt jedoch nicht im
Kommutierungskreis der Halbbrücke. Über diesen Bonddraht fließt nur der niederfrequente
Laststrom und nicht der hochfrequente Kommutierungsstrom. Deshalb fallen an diesem
Rahmenbonddraht des AC-Lastanschlusses trotz seiner verhältnismäßig hohen Induktivität
keine hohen Spannungen ab. Die koppelnde Induktivität zwischen Lastkreis und Steuerkreis
ist nicht größer als bei einem Modul mit Hilfsemitteranschlüssen aus Abbildung 72. Somit
kann auf diesen Hilfsemitterpin verzichtet werden. Die optimale Ausführungsform ergibt sich
somit zu:
Modulpin
DC positiv
LRB
LCU
Modulpin
Gate upper
T1
LRB
CZK
LCU
LCU
LSB
Driver upper
D1
LSB
LSB
LCU
LCU
LRB
Modulpin
AC und
Hilfsemitter
upper
LCU
Modulpin
Gate lower
LCU
T2
LRB
LCU
LSB
LRB
LCU
LSB
LSB
D2
LCU
Driver lower
Modulpin
Hilfsemitter
lower
LSB
LCU
LRB
Modulpin
DC negativ
Abbildung 75: Optimiertes Modul mit unterem Hilfsemitterpin
91
LSB
3 Auslegung des Sinus-Ausgangsfilter
3.1 Bestimmung der auslegungsrelevanten Ausgangsspannung
Der
Wechselrichter
eines
Frequenzumrichters
erzeugt
an
seinem
Wechselspannungsausgang gepulste Ausgangsspannungen, deren Grundfrequenz für die
Drehung des Motors genutzt wird [26]. Beim Zweipunkt-Wechselrichter werden hierbei die
Wechselspannungsanschlüsse U, V und W wahlweise mit dem positiven oder dem negativen
Zwischenkreisspannungspotenzial verbunden.
Für die Beschreibung des Sinusfilters und dessen Dimensionierung ist es zweckmäßig, die
Ausgangsspannung des Umrichters in einen symmetrischen und einen asymmetrischen
Anteil zu zerlegen. Die symmetrische Ausgangsspannung beschreibt alle Größen, die
zwischen den einzelnen Ausgangsphasen auftreten. Diese Spannung wird in der Literatur
auch als differential mode Spannung oder Gegentaktspannung bezeichnet. Im Gegensatz
hierzu beschreibt die asymmetrische Ausgangsspannung das Verhalten der
Ausgangsphasen gegenüber einem festen Referenzpotenzial, beispielsweise der
Bezugserde oder der negativen Zwischenkreisspannungsschiene. Die asymmetrische
Ausgangsspannung wird in der Literatur als common mode Spannung oder
Gleichtaktspannung bezeichnet [46].
VU
M
VV
VW
VCW
VLW
VCOM
Abbildung 76: Dreiphasiges Ersatzschaltbild des Wechselrichterausgangs
In Abbildung 76 ist der Ausgang des Wechselrichters dargestellt. Die gepulsten
Ausgangsspannungen des Wechselrichters werden in diesem Fall auf die negative
Zwischenkreisspannung bezogen. Die Gleichtaktspannung des Systems tritt am Sternpunkt
des Filterkondensators auf. Sie berechnet sich zu:
U COM =
U U + UV + UW
3
(66)
Bilden sowohl der Filter als auch der Motor eine ideal symmetrische Last, so tritt diese
asymmetrische Spannung in gleicher Weise auch an dem Motorsternpunkt auf. Die
asymmetrische Spannung führt in dem Ersatzschaltbild nach Abbildung 76 zu keinem
Stromfluss, sondern lediglich zu einer Potenzialverschiebung des Systems gegenüber dem
Referenzpunkt, weil keine Lastverbindung zu dem Referenzpunkt existiert. In einer
realistischen Anwendung werden jedoch solche Lastverbindungen zumindest aufgrund von
92
parasitären Kapazitäten, z.B. der Motorwicklungen gegen das Motorgehäuse, existieren. Die
Auswirkungen des asymmetrischen Spannungsanteils werden in Kap. 3.4 untersucht.
Da bei üblichen Modulationsverfahren nie zwei Ausgangsphasen gleichzeitig mit
entgegengesetzter Polarität ihr Potenzial ändern, geht aus Gl. (66) hervor, dass jede
Schalthandlung eine Veränderung der common mode Spannung zur Folge hat, wobei die
Änderungsgeschwindigkeit der common mode Spannung identisch zu einem Drittel
Spannungsflanke der schaltenden Wechselrichterausgangsspannung (s. Gl. (66)) ist. Dieses
Verhalten stellt erhöhte Anforderungen an die Isolationsfestigkeit des Motors. Da der in
Abbildung 76 dargestellte Filter keine Bauteile gegenüber dem Referenzpotenzial aufweist,
reduziert er auch nicht die Spannungssteilheit gegenüber dem Referenzpotenzial. Bei der
Beschreibung des Filterverhaltens wird dieser Punkt in einem späteren Kapitel noch
diskutiert.
Die symmetrische Ausgangsspannung ergibt sich nach Abbildung 76 aus der Differenz der
Wechselrichterausgangsspannung – beispielsweise Phase W - und des asymmetrischen
Spannung:
UWD = UW − U COM
(67)
Ein Beispiel für eine symmetrische Spannung ist für Sinus-Dreieck-Modulation mit einem
Aussteuergrad von 90%, einer Grundfrequenz der Ausgangsspannung von 50Hz und einer
Schaltfrequenz von 16kHz in Abbildung 77 dargestellt:
1
1
0.5
UWD( x )
0
0.5
1
1
0
0.002
0.004
0.006
0.008
0.01
0.00
0.012
0.014
x
0.016
0.018
1
fa
Abbildung 77: Kurvenform einer symmetrischen Ausgangsspannung
Diese symmetrische Spannung durchläuft den Sinusfilter, an dessen Ausgang die Spannung
des Filterkondensators als sinusförmige Spannung vorliegen soll. Deshalb ist diese
symmetrische Spannung maßgebend für die Dimensionierung des symmetrischen Filters.
Der sinusförmige Verlauf der symmetrischen Ausgangsspannung bietet den Vorteil der
Vermeidung von Oberschwingungsströmen im Motor. Da Oberschwingungsströme nicht zur
Wandlung der elektrischen in mechanische Energie beitragen, sondern lediglich Verluste im
Motor erzeugen, sollen diese vorrangig vermieden werden.
Eine Fourieranalyse der Kurvenform aus Abbildung 77 zeigt die wesentlichen
Frequenzanteile, die in der symmetrischen Ausgangsspannung enthalten sind:
93
0.4
UWD/UZK
0.3
VWD 0.2
j
0.1
0
0
0
0
4
1 .10
4
2 .10
4
3 .10
4
4 .10
4
5 .10
Frequenz
j
4
6 .10
4
7 .10
4
8 .10
4
9 .10
5
1 .10
100000
f
Abbildung 78: Betrag des Effektivwertes der Frequenzanteile der symmetrischen
Ausgangsspannung (Strangspannung) bei 90% Aussteuergrad, Grundfrequenz 50Hz und
Schaltfrequenz 16kHz
Neben der Grundfrequenz, die mit einer Amplitude von ca. 32% auftritt, sind die
Oberschwingungen mit den Seitenbändern der Schaltfrequenz und ihrer Vielfachen
dominant. Mit zunehmender Ordnungszahl der Vielfachen der Schaltfrequenz nimmt die
Amplitude ab. Das Spektrum der Oberschwingungen ist von dem Modulationsgrad und der
Modulationsart abhängig. Für die Dimensionierung der Filterdrossel sind die dominanten
Spannungsanteile und der Stromfluss, der durch diese hervorgerufen wird, maßgebend. Bei
Sinus-Dreieck-Modulation wird als Modulationsgrad das Verhältnis des Scheitelwertes der
sinusförmigen Steuerspannung zur Dreieckspannung definiert. Abhängig vom
Modulationsgrad betragen die Amplituden der Seitenbänder der niedrigsten Vielfachen der
Schaltfrequenz:
94
14
12
Vh/Vzk/[%]
10
1*fs±2*fout
2*fs±fout
3*fs±4*fout
3*fs±2*fout
4*fs±*fout
5*fs±*2fout
8
6
4
2
0
0
20
40
60
80
100
Modulationsgrad/[%]
Abbildung 79: Seitenbänder der Vielfachen der Schaltfrequenz in der symmetrischen
Ausgangsspannung
Der höchste Frequenzanteil liegt bei mittlerem Modulationsgrad bei den Seitenbändern der
doppelten Schaltfrequenz. Allerdings ist zu berücksichtigen, dass der Stromfluss, den ein
Frequenzanteil zur Folge hat, umgekehrt proportional zur Frequenz ist, da die Impedanz der
Filterdrossel linear mit der Frequenz steigt (ZL = jwL). Deshalb wird der größte Stromfluss
von den Seitenbänden der einfachen Schaltfrequenz bei maximaler Aussteuerung
hervorgerufen.
Dieser
schaltfrequente
Strom
ist
daher
dominant
für
die
Drosseldimensionierung.
Das wesentliche Augenmerk bei der Dimensionierung der Filterkomponenten liegt auf der
Auslegung der Filterdrossel, da diese das dominante Bauteil bezüglich Kosten und
Bauvolumen darstellt. Deshalb sollen im Folgenden zunächst Dimensionierungskriterien für
die Drossel betrachtet werden.
Ist die Last des Umrichters wie in Abbildung 76 dargestellt in allen Phasen identisch, so kann
das dreiphasige durch ein einphasiges Ersatzschaltbild ersetzt werden. Für die
Drosselauslegung werden dabei nur die symmetrischen Spannungskomponenten betrachtet:
iLF
UWD
LF
ULF
LM
CF
ULM
UCF
UiM
Abbildung 80: Einphasiges symmetrisches Ersatzschaltbild
Der Motor ist in diesem Modell als Reihenschaltung einer Spannungsquelle und einer
Induktivität, wobei die Spannungsquelle der EMK entspricht und die Induktivität die
95
Streuinduktivität des Motors nachbildet. Diese Ersatzvorstellung ist in der Literatur weit
verbreitet [80] und liefert für grundlegende Betrachtung ausreichende Ergebnisse.
Der Strom in der Filterinduktivität berechnet sich dann zu:
t
i LF (t ) =
∫ (U
WD
(τ ) − U CF (τ ))dτ
t =t 0
LF
(68)
+ i LF (t = t 0 )
Diese Gleichung beschreibt den Drosselstrom für alle Frequenzen. Um die Auslegung der
Drossel zu vereinfachen, ist es zweckmäßig, einzelne Frequenzanteile getrennt zu
betrachten.
Zum einen enthält die symmetrische Spannung des Umrichters die Grundfrequenz, die die
Drehzahl des Motors bestimmt. Diese ist relativ niederfrequent und liegt im Bereich bis ca.
200Hz. Da die Filterinduktivität im Vergleich zur Streuinduktivität des Motors deutlich
geringer sein wird, kann der Spannungsabfall an der Filterinduktivität in erster Näherung
vernachlässigt werden. Eine ähnliche Betrachtung gilt für den Filterkondensator. Bei der
niedrigen Grundfrequenz stellt dieser Kondensator eine sehr hohe Impedanz dar. Deshalb
fließt in den Filterkondensator in erster Näherung kein grundfrequenter Strom bzw. dieser ist
so gering, das er für die thermische Dimensionierung der Drossel vernachlässigt werden
kann.
Der grundfrequente Strom sieht mit dieser Vereinfachung nur die Motorkomponenten als
Last. Das Ersatzschaltbild für die grundfrequenten Größen vereinfacht sich demnach zu:
LM
iLF1
ULM
UWD1
UiM
Abbildung 81: Vereinfachtes Ersatzschaltbild für grundfrequente Größen
Die zugehörige Berechnungsgleichung für den grundfrequenten Strom lautet:
t
i LF 1 (t ) =
∫ (U
WD1
(τ ) − U iM (τ ))dτ
t =t 0
LM
+ i LF 1 (t = t 0 ),
(69)
Der Index 1 deutet hierbei darauf hin, dass es sich jeweils um grundfrequente Größen
handelt.
Eine analoge Vereinfachung ist für die Größen möglich, die mit den Seitenbändern der
Schaltfrequenz und deren Vielfachen auftreten. Für diese Ströme stellt die Streuinduktivität
des Motors eine sehr hohe Impedanz dar. In erster Näherung kann deshalb kein
hochfrequenter Strom in den Motor fließen. Der Filterkondensator stellt für die
hochfrequenten Ströme hingegen eine sehr geringe Impedanz dar. Betrachtet man den
idealisierten Fall einer rein sinusförmigen Filterausgangsspannung, so erzeugen die
hochfrequenten Stromanteile keinen Spannungsabfall an dem Filterkondensator, der für
96
diese somit als Kurzschluss wirkt. Das einphasige Ersatzschaltbild für die hochfrequenten
Größen ist demnach:
LF
iLFh
ULF
UWDh
Abbildung 82: Vereinfachtes Ersatzschaltbild für hochfrequente Größen
Der hochfrequente Strom sieht als Last demnach nur die Filterkomponenten. Die zugehörige
Gleichung zur Berechnung des hochfrequenten Stromes lautet entsprechend:
t
i LFh (t ) =
∫U
WDh
(τ )dτ
(70)
+ i LFh (t = t 0 ),
t =t 0
LF
Der Index h deutet darauf hin, das es sich bei dieser Gleichung um hochfrequente Größen
handelt, die mit den Seitenbändern der Schaltfrequenz und deren Vielfachen auftreten.
Der gesamte Drosselstrom ergibt sich durch die Addition von Gl. (69) und Gl. (70):
t
i LF (t ) =
∫ (U WD1 (τ ) − U iM (τ ))dτ
t =t 0
LM
t
+
∫U
WDh
(τ )dτ
+ i LF (t = t 0 ),
t =t 0
LF
(71)
Da der niederfrequente Strom in der Filterdrossel nahezu keine Eisenverluste verursacht,
werden diese in erster Linie durch Gl. (70) bestimmt. Für die magnetische Auslegung ist der
grundfrequente Strom dennoch relevant, da er zu Sättigungserscheinungen in der Drossel
führen kann. Bei der Berechnung der Kupferverluste sind sowohl der niederfrequente als
auch der hochfrequente Strom zu berücksichtigen, wobei letzterer noch durch den Skineffekt
beeinflusst wird.
Für die erforderliche Induktivität der Drossel ist mit der vereinfachten Betrachtung nur Gl.
(70) maßgebend.
3.2 Auslegung der Filterdrossel
Aus rein technischen Überlegungen resultieren bei gegebenem Kernmaterial der Aufwand
und die Kosten für eine Filterinduktivität in erster Linie aus deren Baugröße und dem
Kilopreis des verwendeten Kernmaterials und des Kupfers. Die Baugröße der Drossel wird
im Wesentlichen durch zwei Kriterien bestimmt:
¾ Bei der magnetischen Dimensionierung ist darauf zu achten, dass der Kern die
erforderliche magnetische Energie speichern kann, ohne in Sättigung zu gehen.
¾ Bei der thermischen Dimensionierung ist eine Überhitzung der Drossel zu vermeiden.
97
3.2.1 Magnetische Dimensionierung der Filterdrossel
3.2.1.1 Grundlagen
Für die Veranschaulichung der folgenden grundlegenden Überlegungen wird eine typische
Querschnittsansicht einer einphasigen Drossel betrachtet [19]:
A
n·I
H,B
n·I
Abbildung 83: Querschnitt durch eine einphasige Filterdrossel
Durch den Stromfluss in dem Wicklungsfenster wird im Kern ein magnetischer Fluss erzeugt.
Grundlegend beschrieben wird dieser Zusammenhang in dem Durchflutungsgesetz, das in
seiner allgemeinen Form lautet:
∫H ds = Θ
(72)
l
Ist der Betrag des Vektors der magnetischen Erregung H konstant und seine Richtung
immer parallel zu der Richtung der Teilabschnitte d s des Umlaufs mit der Gesamtlänge l
und besteht die Gesamtdurchflutung Θ aus n in Reihe geschalteten Windungen, die jeweils
den Strom I führen, so vereinfacht sich Gl. (72) zu:
H ⋅l = n⋅ I
(73)
Hierbei wird l als der mittlere Eisenweg in der Spulengeometrie angenommen.
In einigen Fällen werden Drosseln der Bauart nach Abbildung 83 mit einem Luftspalt
ausgeführt. Bei der Einführung der magnetischen Flussdichte B in Abhängigkeit der
magnetischen Erregung H sind dann die unterschiedlichen Permeabilitäten in Kern und
Luftspalt zu berücksichtigen. In vielen Fällen werden wird jedoch auch als Kernmaterial
Eisenpulver eingesetzt, welches einen verteilten Luftspalt darstellt. Diese Lösung bietet den
Vorteil, dass die Verluste gleichmäßiger auf das Kernmaterial verteilt werden, weil an einem
konzentriertem Luftspalt Feldlinien in die Wicklung eindringen und dort lokal hohe
Wirbelstromverluste erzeugen können [4].
Bei verteiltem Luftspalt kann von einer homogenen Verteilung der magnetischen Erregung
ausgegangen werden. Das Durchflutungsgesetz lautet dann:
B
μ
⋅l = n⋅ I
(74)
Der Fluss im Kernmaterial berechnet sich als Integral der Flussdichte über den
Kernquerschnitt:
98
Ψ = ∫ Bd A
A
(75)
FE
bzw. für den Fall, dass der Flussdichtevektor senkrecht auf der betrachteten Fläche A steht
und sein Betrag über der Fläche A konstant ist:
Ψ = Β ⋅ Α FE
(76)
Die Selbstinduktivität L der Spulenanordnung ist definiert als Proportionalitätsfaktor zwischen
dem Erregerstrom und dem Fluss, der sich bei einer Windung ergibt:
L=
Φ
I
(77)
Der Gesamtfluss in der Spulenanordnung ergibt sich aus der Summe aller Teilflüsse, die sich
pro Windung ergeben. Sind alle Teilflüsse identisch, so gilt für den Gesamtfluss:
Ψ = n⋅Φ
(78)
Setzt man Gl. (74), Gl. (76) und Gl. (78) in Gl. (77) ein, so ergibt sich für die Induktivität:
n 2 μ AFE
L=
l
(79)
Die Energie, die in einer Drossel gespeichert werden kann, beträgt
1
2
1
=
2
1
=
2
1
=
2
E=
L I2
n 2 μ AFE 2
I
l
nI μ
n I AFE
l
(80)
n ACU J AFE B
Aus den letzten beiden Zeilen von Gl. (80) lässt sich eine Abschätzung für die Baugröße der
Drossel ableiten. Mit der Wahl eines Kernmaterials ist die maximal zulässige magnetische
Flussdichte B definiert. Daraus folgt, dass bei gegebener magnetischer Weglänge l das
Produkt n • I und damit die zulässige Durchflutung begrenzt ist. Eine Erhöhung der Energie
kann somit nur unter Erhöhung des Kernquerschnitts AFE erfolgen. Stellt man sich eine
Drossel mit dem Querschnitt aus Abbildung 83 als quaderförmiges Gebilde vor, so bedeutet
eine Vergrößerung von AFE unter Beibehaltung von l eine Ausdehnung der Drossel in die
Zeichenebene hinein und somit eine lineare Volumenszunahme mit der gespeicherten
Energie.
Alternativ könnte die Durchflutung n • I erhöht werden. Um eine Überschreitung der
maximalen Flussdichte zu verhindern, müsste in gleichem Maß die effektive Weglänge l
vergrößert werden. Bei einer Drossel mit Luftspalt würde dies bedeutet, dass der Luftspalt
vergrößert werden muss, bei verteiltem Luftspalt muss die effektive Permeabilität µ reduziert
werden. Die Energie der Drossel würde bei konstantem B linear mit n • I ansteigen. Geht
99
man davon aus, dass die maximal zulässige Stromdichte J im Kupferdraht bereits
ausgenutzt wurde, so kann n • I nur durch eine Zunahme des Kupferquerschnitts erhöht
werden. Legt man wieder den Querschnitt nach Abbildung 83 zu Grunde, erfordert dies ein
linear vergrößertes Wickelfenster bei konstant verbleibendem Eisenquerschnitt.
Beide Maßnahmen führen zu einer nahezu linearen Zunahme des Drosselvolumens mit der
gespeicherten Energie. Im Umkehrschluss folgt daraus, dass ein minimales Drosselvolumen
und damit verbunden ein minimaler Aufwand für die Drossel dann erreicht werden kann,
wenn die in der Drossel zu speichernde Energie minimal wird.
3.2.1.2 Bestimmung des Ripplestroms
Für einen gegebenen Grundschwingungsstrom lässt sich aus Gl. (80) ein optimaler
hochfrequenter Ripplestrom berechnen, der das geringste Drosselvolumen erfordert. Dieser
Überlegung liegt das Ersatzschaltbild für die hochfrequenten symmetrischen
Spannungsanteile aus Abbildung 82 zu Grunde. Innerhalb einer Modulationsperiode wird
davon ausgegangen, dass sich die Spannung am Filterkondensator nicht ändert, während
die gepulste Spannungsquelle innerhalb der Modulationsperiode einmal umschaltet. Der
grundfrequente Strom sei während dieser Modulationsperiode konstant, der Mittelwert der
gepulsten Spannung sei deshalb gleich null. Der maximale Ripplestrom, auf den die Drossel
ausgelegt sein muss, stellt sich genau dann ein, wenn die Spannung am Filterkondensator
gleich die Hälfte des Spannungshubs der gepulsten Spannung beträgt und der
Aussteuergrad der gepulsten Spannung 50% beträgt. In diesem Fall ergibt sich folgender
Stromverlauf:
I
I1+Ih
I1
Îh
t
Modulationsperiode tp
Abbildung 84: Verlauf des Ripplestromes
Die maximale Energie, auf die diese Drossel ausgelegt sein muss, beträgt:
E max =
(
1
L Î1 + Î h
2
)
2
(81)
Bei konstanter treibender Spannung und nicht gesättigtem Kernmaterial gilt als
Randbedingung:
100
UL tp
Îh
⇒ Îh =
tp
4L
4
UL = L
(82)
Eingesetzt in Gl. (81) ergibt sich für die maximal zu speichernde Energie
UL tp
1 ⎛
= L ⎜⎜ Î 1 +
2 ⎝
4L
E max
⎞
⎟⎟
⎠
2
(83)
und den maximal auftretenden Strom:
I max = Î1 +
UL tp
(84)
4L
Bei fest vorgegebenen Werten für die treibende Spannung (im Allgemeinen die
Zwischenkreisspannung) und die Modulationsperiode können Energie und maximaler Strom
als Funktion der Induktivität angegeben werden. Aus Gründen der Vergleichbarkeit sei
definiert:
UL tp
Lref =
(85)
4 Î1
Dies bedeutet anschaulich, dass bei der Induktivität Lref die Amplitude des Ripplestroms
genauso groß ist wie der Scheitelwert des Grundschwingungsstroms. Energie und
maximaler Drosselstrom als Funktion der Induktivität ergeben sich dann zu:
5
5
4
Emax
Emax
Imax
I
L
Lref
L
3
2
1
1
0
0
0
1.5
3
4.5
6
7.5
0
9
10.5
12
L
13.5
15
15
Lref
Abbildung 85: Energie und maximaler Drosselstrom als Funktion der Induktivität
Die geringste Energie in der Drossel – und damit nach Gl. (80) das geringste Bauvolumen –
ergeben sich, wenn die Induktivität so gewählt wird, dass der Ripplestrom und der
Grundschwingungsstrom identische Amplituden besitzen. Nach Gl. (84) ist der Ripplestrom
unabhängig von der augenblicklichen Last des Umrichters. Der Grundschwingungsstrom ist
jedoch sinusförmig und lastabhängig, so dass sich die Frage stellt, auf welchen
Augenblickswert des Grundschwingungsstroms das Diagramm in Abbildung 85 zu beziehen
ist. Für eine Minimierung der gespeicherten Energie in der Drossel muss der maximale in der
101
Drossel auftretende Augenblickswert des Grundschwingungsstromes herangezogen werden,
weil in diesem Betriebspunkt die größte in der Drossel anfallende Energie auftritt. In letzter
Konsequenz wäre dies der Abschaltstrom des Umrichters im Fehlerfall, d.h. die
Ansprechschwelle der umrichterinternen Schutzmaßnahmen.
Bei dieser Auslegung ist jedoch zu berücksichtigen, dass dann im Normalbetrieb des
Umrichters der Ripplestrom deutlich größer als der Grundschwingungsstrom sein würde. In
Abbildung 85 entspricht dies einem Betrieb deutlich links vom Optimum, die gespeicherte
Energie und der Ripplestrom in der Drossel wären im Normalbetrieb weitaus größer als
eigentlich erforderlich. Die Randbedingung für die Dimensionierung des Ripplestroms auf
minimale Energiespeicherung in der Drossel war nach Gl. (80) dass eine Sättigung der
Drossel vermieden werden sollte. Für eine konkrete Anwendung ist jedoch zu überlegen, ob
in Fehlerfällen des Umrichters wie einer Überstromabschaltung eine Sättigung der
Filterdrossel akzeptiert werden kann.
3.2.2 Thermische Dimensionierung der Filterdrossel
Für die Drosselverluste existieren im Wesentlichen drei Ursachen:
3.2.2.1 Kupferverluste
Die Kupferverluste in der Drossel werden durch den ohmschen Widerstand der Wicklung
verursacht. Sie sind proportional zu dem spezifischen Widerstand des Leitermaterials und
der Länge einer Wicklung. Vernachlässigt man Skin- und Proximityeffekte, so sind die
Kupferverluste unabhängig von der Frequenz des fließenden Stromes. Diese
Vernachlässigung ist im Fall des Demonstrators zulässig, da die Schaltfrequenz von 16kHz
für diese Effekte klein ist und daher eine untergeordnete Rolle spielt. Der überwiegende Teil
der Kupferverluste wird durch den grundfrequenten Strom verursacht.
3.2.2.2 Hystereseverluste
B
2
Bmax
3
1
H
5
4
-Bmax
Abbildung 86: Typische Hysteresekennlinie eines Magnetmaterials
102
Wird die Stromstärke in einer nicht vormagnetisierten Drossel nach Abbildung 83 von null
aus bis zu seinem Maximalwert erhöht, so steigt proportional die magnetische Erregung H an
(s. Gl. (73).) Gemäß der Magnetisierungskennlinie des Magnetmaterials steigt auch die
magnetische Flussdichte B an.
Auf der Kennlinie wird während dieses Vorgangs der Bereich zwischen den Punkten 1 und 2
durchschritten. In dem Magnetmaterial wird hierbei die magnetische Energiedichte
W mag =
Bmax
∫ H dB
(86)
0
gespeichert [19]. Anschaulich entspricht dies der Fläche, die von der Kurve zwischen den
Punkten 1 und 2, der Ordinate B und der Waagrechten B=Bmax begrenzt wird. Das Integral
der magnetischen Energiedichte über das Volumen des Magnetkernes ergibt die im
Magnetmaterial gespeicherte Energie. Diese Energie muss von extern zugeführt werden.
Wird der Strom anschießend bis auf null reduziert, so reduziert sich die magnetische
Flussdichte gemäß der Kennlinie zwischen den Punkten 2 und 3. Während dieses Vorgangs
wird Energie aus dem Magnetmaterial zurück gewonnen, die der Fläche entspricht, die von
der Kennlinie zwischen den Punkten 2 und 3 sowie der B-Ordinate und der Waagrechten
B=Bmax begrenzt wird. Da die magnetische Flussdichte nicht auf den Wert 0 zurückgeht,
sondern bei H=0 bei dem Wert an Punkt 3 verbleibt, der auch als Remanenzflussdichte
bezeichnet wird, ist diese zurück gewonnene Energie geringer als die zuvor aufgewendete
Energie.
Steigt anschließend der Strom bis auf seinen negativen Maximalwert an, ist wiederum
Energie aufzuwenden, deren Betrag der Fläche entspricht, die von der
Magnetisierungskennlinie zwischen den Punkten 3 und 4, der B-Ordinate und der
Waagerechten B=-Bmax begrenzt wird. Diese Energie ist wiederum größer als die
anschließend zwischen den Punkten 4 und 5 zurück gewonnene Energie. In Abbildung 86 ist
in jedem Zyklus die Differenz zwischen aufgenommener und zurück gewonnener Energie der
Fläche zwischen den beiden Ästen der Magnetisierungskennlinie proportional.
Somit führt die Hysterese zu Verlusten, deren Betrag zur Frequenz des speisenden Stromes
proportional ist, weil bei jedem Zyklus eine Energiemenge aufgewendet werden muss.
Deshalb ist es für die Anwendung als Sinusfilterdrossel vorteilhaft, wenn die
eingeschlossene Fläche zwischen den beiden Ästen der Kennlinie möglichst klein ist.
Allerdings ist zu berücksichtigen, dass der dargestellte Vorgang in der Form nur für
Stromformen gilt, bei denen in jeder Periode sowohl die maximale als auch die minimale
magnetische Flussdichte erreicht werden. In der Anwendung der Sinusfilterdrossel ist dies
jedoch nicht der Fall. In der Sinusfilterdrossel fließt ein hoher grundfrequenter Strom, der von
einem betragsmäßig deutlich kleineren Strom mit Schaltfrequenz und deren Vielfachen
überlagert wird.
In der Literatur ([98], [99], [118]) sind die Hystereseverluste bei Stromkurvenformen mit
hochfrequenten Oberschwingungen analysiert worden. Hierbei wird die grundfrequente
Magnetisierungskennlinie als „parent loop“ bezeichnet. Innerhalb dieser bilden sich
sogenannte „minor loops“ mit der Amplitude der Oberschwingung aus.
103
I(t)
B
2
Bmax
2
2
3
X
3
1
5
H
t
Y
5
Y
X
X
-Bmax
4
4
Abbildung 87: Hysterese bei Stromkurvenformen mit unterschiedlichen Frequenzanteilen
In Abbildung 87 ist eine derartige „minor loop“ sowie ein zugehöriger Stromverlauf qualitativ
grafisch dargestellt. Der Strom steigt zunächst vom Punkt 3 zum Punkt X in negativer
Richtung an. Am Punkt X wechselt die Ableitung des Stromes aufgrund eines
hochfrequenten Anteiles das Vorzeichen. Die Magnetisierungskennlinie verläuft nun zum
Punkt Y, wobei die Steigung der Kurve von X nach Y aus dem Mittelwert der beiden zuletzt
positiv und negativ durchlaufenen Kurvenäste bei der betreffenden Flussdichte gebildet wird.
Im vorliegenden Fall sind dies die Kurvenäste von 4 nach 5 und von 3 nach 4.
Am Punkt Y wechselt die Ableitung des Stromes wieder das Vorzeichen. Die
Magnetisierungskennlinie verläuft von Y nach 4, wobei die Steigung aus dem Mittelwert der
Steigungen der Kurvenäste zwischen X und Y sowie zwischen 3 und 4 ermittelt wird.
In Abbildung 87 ist aus Gründen der Übersichtlichkeit nur eine hochfrequente Schwingung
dargestellt. Die Überlegungen gelten selbstverständlich analog für alle Orte auf der
Magnetisierungskennlinie.
3.2.2.3 Wirbelstromverluste
Die Entstehung der Wirbelströme ist in Abbildung 88 dargestellt:
y
z
y
Schnitt AA’
H,B
x
A
n·I
n·I
z
x
Iw
A’
H,B
R
dx
dx
Abbildung 88: Entstehung von Wirbelströmen
Ein Primärstrom I führt in der Anordnung nach Abbildung 88 zu einem magnetischen Fluss in
dem Kernmaterial. Ist der Primärstrom eine zeitabhängige Größe mit rein sinusförmigem
Verlauf, so gilt für den Gesamtfluss nach Gl. (76) und Gl. (74):
104
Ψ (t ) = AFE µ0 µr
n ˆ
I sin( wt )
(87)
l FE
Die Flussrichtung ist in dem Schnittbild entlang des Schnittes AA’ im rechten Teil von
Abbildung 88 dargestellt. Denkt man sich nun eine Leiterschleife in der xy-Ebene, die in
Abbildung 88 rot dargestellt ist, so wird durch den zeitveränderlichen Fluss in dieser
Leiterschleife eine Spannung induziert:
U w (t ) = −
n ˆ
dΨ (t )
= − AFE µ0 µr
I w cos( wt ) = R I w (t )
l FE
dt
(88)
Diese induzierte Spannung ist die treibende Spannung für die Wirbelströme. Der Widerstand
R der Leiterschleife berechnet sich aus dem spezifischen Leitwert des ferromagnetischen
Materials und der Länge der Leiterschleife. Die Amplitude der Wirbelströme ist proportional
zur Frequenz des Wirbelstromes und somit auch proportional zur Frequenz des
Primärstromes I. Die von Wirbelströmen verursachen Verluste steigen deshalb quadratisch
mit der Amplitude des Wirbelstromes und somit quadratisch mit der Frequenz des
Primärstromes. Bei Kurvenformen des Primärstromes mit beliebigem Verlauf gelten diese
Überlegungen analog für alle Anteile der zugehörigen Fourierreihe.
Eine Maßnahme zur Reduzierung der Wirbelstromverluste besteht darin, die wirksame
elektrische Leitfähigkeit des ferromagnetischen Materials zu reduzieren. Im Fall von Kernen
aus Eisen, das eine hohe spezifische Leitfähigkeit besitzt, wird statt eines massiven
Eisenkernes eine Vielzahl einzelner, dünner Bleche in y-Richtung zu einem Kern
geschichtet. Die Bleche sind elektrisch gegeneinander isoliert, so dass die elektrische
Leitfähigkeit in y-Richtung verschlechtert wird. Andere Materialien wie Ferrite oder
Eisenpulver werden mit geringer elektrischer Leitfähigkeit hergestellt, so dass in diesen
Fällen massive Kerne verwendet werden können.
3.2.2.4 Integrations- und Kühlkonzept für den Sinusfilter
Neben den Verlusten wird die Baugröße der Filterdrossel auch durch die Art der
Entwärmung
beeinflusst,
weil
letztendlich
die
durch
Verluste
verursachte
Temperaturerhöhung an der Drossel begrenzt werden muss. Standardmäßige Sinusfilter
werden als Optionen zu Standardumrichtern angeboten. Diese Sinusfilter beinhalten eine
Filterdrossel und einen Filterkondensator und sind in einem eigenen Gehäuse aufgebaut. Die
Kühlung des Sinusfilters erfolgt mittels natürlicher Konvektion über das Gehäuse.
Wird der Sinusfilter in das Gehäuse des Umrichters integriert, so bietet diese Lösung den
Vorteil, dass der Sinusfilter mit Zwangsbelüftung entwärmt werden kann, da Umrichter im
betrachteten Leistungsbereich in der Regel mit einem Lüfter gekühlt werden.
IGBT-Modul
Drossel
Lüfter
Kühlkörper
Strömungsrichtung der Luft
Abbildung 89: Anordnung zur forcierten Luftkühlung der Filterdrossel
105
Die Verluste der Sinusfilterdrossel sind hierbei gegenüber den Verlusten des
Filterkondensators dominant, so dass vor allem die Drosseln einen Vorteil bei forcierter
Luftkühlung erfahren. Durch die forcierte Kühlung können zwar nicht die Verluste der Drossel
reduziert werden, aber der Wärmewiderstand der Drossel kann reduziert werden. Zur
quantitativen Bewertung wurden zwei identische Drosseln in Reihe geschaltet, wobei eine
Drossel in einem forcierten Luftkanal liegt, während die zweite Drossel konvektionsgekühlt
ist. Beide Drosseln wurden anschließend mit Gleichstrom beaufschlagt. Eine Messung unter
Last am Umrichter ist nicht erforderlich, da es für den Wärmewiderstand unerheblich ist, ob
Eisenverluste oder Kupferverluste die Ursache der Erwärmung darstellen.
25
20
delta T/[K]
natürliche Kühlung
15
10
5
forcierte Kühlung
0
0
5
10
15
20
25
30
I/[A]
Abbildung 90: Temperaturerhöhung bei natürlicher und forcierter Kühlung der
Sinusfilterdrossel mit einem Volumenstrom von 0,022m3/s
Der Temperaturhub der Drossel steigt quadratisch mit dem Strom, da bei Gleichstrom nur
Kupferverluste anfallen. Aus Abbildung 90 ist ersichtlich, dass für die Drossel im Luftkanal
die Temperaturerhöhung auf 29% gesenkt werden kann.
Dieser Wert kann nun auf den Nennbetrieb umgerechnet werden. Die standardmäßige
Umgebungstemperatur beträgt 40°C. Die maximal zulässige Drosseltemperatur hängt von
den verwendeten Materialien ab, begrenzend wirken hier i.a. die Kunststoffe, z.B.
Kabelisolierungen. Als typischer Wert kann 125°C genannt werden. Somit ergibt sich eine
zulässige Temperaturerhöhung an der Drossel von 85K. Nimmt man dies als Referenzwert
der konvektionsgekühlten Drossel, so könnte durch den Einsatz der forcierten Kühlung der
Temperaturhub auf 25K reduziert werden.
Allerdings ist zu berücksichtigen, dass der Kühlkörper, über den der IGBT entwärmt wird, für
eine Vorheizung der Kühlluft für die Drossel sorgt. Aus Messungen an einem
Demonstratoraufbau nach Abbildung 89, in dem die Drossel nicht bestromt wurde, wurde
eine Temperaturerhöhung an der Drossel von 14K gemessen. Dieser Wert ist von dem
eingesparten Temperaturhub durch die forcierte Kühlung abzuziehen. In Summe kann die
Temperaturerhöhung gegenüber der konvektionsgekühlten Drossel um 46K oder 54%
reduziert werden. Dieser Vorteil, dass der thermische Widerstand der Drossel mehr als
halbiert wird, kann für eine Reduzierung der Baugröße der Drossel verwendet werden, weil
neben der in Kap. 3.2.1. beschriebenen magnetischen Auslegung auch die thermische
Dimensionierung berücksichtigt werden muss.
106
Neben dem Vorteil für die Sinusfilterdrossel ist jedoch zu berücksichtigen, dass durch den
zusätzlichen Einbau der Drossel in den Kühlkanal der Druckabfall ansteigt. Dies führt zu
einer Reduzierung der Fördermenge des Lüfters und somit zu einem erhöhten
Wärmewiderstand des Kühlkörpers bzw. einem erhöhten Halbleiterbedarf. Der Druckabfall
an der Drossel hängt stark von deren Größe, Bauform und Anordnung ab, weil ungünstige
Lösungen starke Verwirbelungen der Luft erzeugen können.
An einer Drosselanordnung aus Schalenkernen wurde die zusätzliche Erwärmung der
Halbleiter ermittelt. Schalenkerne stellen aus strömungstechnischer Sicht aufgrund ihres
runden Querschnitts eine günstige Lösungsvariante dar.
Strömungsrichtung der Luft
Lüfter
Kühlkörper mit
Kühlrippen
Drossel für
3 Phasen
IGBTModul
Temperaturmesspunkt
P = const
Abbildung 91: Versuchsaufbau zur Bestimmung der Rückwirkung der Sinusdrossel auf die
Halbleiterkühlung
In einem Versuchsaufbau nach Abbildung 91wurde ein IGBT-Modul auf einen Kühlkörper
montiert, die IGBTs dauerhaft eingeschaltet und eine definierte Verlustleistung eingespeist.
Unter dem IGBT-Modul wurde die Kühlkörpertemperatur mit einem Thermoelement
gemessen. Die Differenz der gemessenen Temperatur zur Umgebungstemperatur ergibt den
Temperaturhub, aus dem der effektive Wärmewiderstand der Anordnung berechnet werden
kann:
Rth =
ΔT
P
(89)
Dieser Versuch wurde mit folgenden Anordnungen durchgeführt:
1) Drosseln aus dem Luftkanal entfernt (Referenzwert für einen Aufbau ohne
integrierten Sinusfilter)
2) Drosseln im Luftkanal hinter dem Kühlkörper wie in Abbildung 91
3) Drosseln zwischen Lüfter und Kühlkörper
Bei einer eingespeisten
Temperaturerhöhungen:
Verlustleistung
von
107
470
W
ergeben
sich
folgende
Anordnungen
∆T/[K]
∆T relativ
1
2
3
28.2
28.9
36.3
1.000
1.025
1.287
Tabelle 2: Temperaturerhöhung bei unterschiedlichen Anordnungen
Durch die Einführung der Drosseln hinter den Kühlkörper wird der thermische Widerstand
des Kühlkörpers für die Halbleitermodule nur um 2,5% verschlechtert. Werden die
Sinusfilterdrosseln zwischen Lüfter und Kühlkörper platziert, verschlechtert sich der
Kühlkörper um 28%. Dieser Unterschied ist auf den ersten Blick erstaunlich, weil die
Druckabfälle an Kühlkörper und den Drosseln einer Reihenschaltung entsprechen, deren
Wirkung in Summe nicht von der Reihenfolge der Komponenten abhängen sollte. Die
Ursache für den Unterschied liegt in den zusätzlichen Verwirbelungen, die Drosseln
zwischen Lüfter und Kühlkörper bewirken und die die Anströmung der Kühlrippen
verschlechtert. Die Aufbauvariante 3 ist damit nicht vorteilhaft.
Die Reduzierung des thermischen Widerstandes der Sinusfilterdrosseln auf unter 30% bei
der Aufbauvariante 2 ist mit der Erhöhung des thermischen Widerstandes des Kühlkörpers
für die Halbleitermodule um 2,5% bezüglich seiner Auswirkungen auf Kosten und
Performance in Relation zu setzen. Der Demonstratorumrichter wurde in der Aufbauvariante
2 realisiert.
3.2.3 Rückwirkung des Ripplestroms auf die Halbleiterdimensionierung
Neben der Auswirkungen auf die Baugröße der Filterdrossel nach Abbildung 85 besitzt der
Ripplestrom auch eine Rückwirkung auf die Dimensionierung der Leistungshalbleiter des
Wechselrichters. Diese Rückwirkung ist von hoher Bedeutung, da die Leistungshalbleiter des
Wechselrichters einen erheblichen Anteil an den Gesamtkosten des Umrichters verursachen
und somit mögliche Einsparungen am Drosselaufwand zunichte machen könnten.
3.2.3.1 Simulation der zusätzlichen Halbleiterverluste
Da sich der Ripplestrom dem Grundschwingungsstrom überlagert, erhöht er den Effektivwert
des Umrichterausgangsstroms. Im Gegensatz zu der einfachen Modellvorstellung aus
Abbildung 84, mit der eine Abschätzung der erforderlichen Induktivität vorgenommen wurde,
besteht der tatsächliche Ripplestrom aus einer Vielzahl von Frequenzanteilen, die mit den
hochfrequenten Frequenzanteilen der symmetrischen Ausgangspannung nach Abbildung 79
korrelieren. Eine einfache analytische Berechnung der zusätzlichen Wechselrichterverluste –
beispielsweise durch quadratische Addition der einzelnen Effektivwerte – ist deshalb nicht
möglich. Aus diesem Grund wurde für den Umrichter ein Simulationsmodell in Simplorer
aufgebaut, mit dem die Rückwirkungen des Ripplestroms auf die Wechselrichterverluste
abgeschätzt werden sollen. Dieses Simulationsmodell soll im Folgenden kurz vorgestellt
werden.
Die Art der Einspeiseschaltung des Simulationsmodells besitzt für die Bewertung der
Rückwirkungen der Auslegung der Filterdrossel auf die Wechselrichterverluste nur einen
geringen Einfluss, soll hier aus Gründen der Vollständigkeit jedoch trotzdem kurz erläutert
werden.
108
Lu
A
Kondensato
AM2
A
L1
Masse
L1
DCp
L2
DCn
L3
V
V
U
V
DCprein
DCpraus
DCprein
DCnrein
DCnraus
DCnrein
W
W
R11
Lw
+
U_U2
+
V
R8
L1 L2 L3
+
V
U_V1
+
V
I1
V
AM1
U_V2 U_W2
+
V
+
V
A
+
V
U_W1
U_U1
S1
Motor
R10
V
L3
+
Lv
U
L2
+
V
R7
AM3
A
VM1
I_Umot
R9
A
+
Netz
R6
I_Uout
Wechselrichter
F3E
C1
C2
C3
C1_IGBT
C2_Diode
I2
S2
Abbildung 92: Übersichtsbild des Simulationsmodells
Die Netzeinspeisung des Simulationsmodells besteht aus einer dreiphasigen idealen
Spannungsquelle mit einer Amplitude von 690V. Dieser Spannungsquelle wird ein
Innenwiderstand in Reihe geschaltet, dessen Betrag 1% der Umrichternennimpedanz
Unenn/Inenn entspricht. Im Fall des Demonstratorumrichters beträgt die Strangspannung des
Umrichters 400V und sein Nennstrom 23A, so dass sich für den Betrag der Netzimpedanz
ein Wert von 174mΩ ergibt. Dieser Innenwiderstand wird bei einer Frequenz von 50Hz zu 2/3
induktiv und zu 1/3 ohmsch angenommen, wobei sich die Spannungsabfälle an den
Impedanzanteilen geometrisch addieren.
Als Gleichrichter wird in dem Simulationsmodell eine aktive Schaltung verwendet, die in der
Literatur unter dem Begriff „F3E“ (Fundamental Frequency Front End) [43] bekannt ist. Diese
Schaltung besteht aus einer dreiphasigen Brückenschaltung mit IGBTs und Freilaufdioden.
Die Ansteuerimpulse der IGBTs in dieser Brückenschaltung sind identisch zu den
Ansteuerpulsen, die eine Thyristorbrücke erhalten würde, die immer im natürlichen
Zündzeitpunkt betrieben wird. Durch die IGBTs entsteht in dieser Schaltungstopologie der
zusätzliche Freiheitsgrad, die Stromrichtung umzukehren und somit Energie von dem
Zwischenkreis in das Netz zurückzuspeisen.
Der Zwischenkreiskondensator des Umrichters besteht aus einem Kondensator, der im
Vergleich zu konventionellen Spannungszwischenkreisumrichtern um etwa den Faktor 100
reduziert ist. Die Gleichspannung am Zwischenkreiskondensator folgt aufgrund des aktiven
Gleichrichters immer der höchsten verketteten Eingangsspannung und zeigt somit einen
charakteristischen Frequenzanteil, der dem sechsfachen der Frequenz der
Eingangsspannung entspricht. Aufgrund dieses Wechselspannungsanteils wird der
Zwischenkreiskondensator üblicherweise als Folienkondensator ausgeführt. Auf der
Netzseite besitzt die Einspeiseschaltung einen dreiphasigen kapazitiven Filter, der die
erforderlichen Kommutierungspfade für den Wechselrichter bereitstellt und schaltfrequente
Stromanteile vom Netz fernhält. Diesem Filterkondensator ist ein Widerstand in Reihe
geschaltet, der mögliche Schwingungen mit der Induktivität des Netzes bedämpfen soll.
Der Wechselrichter besteht aus einer dreiphasigen IGBT-Brücke mit Freilaufdioden. Der
Steuersatz des Wechselrichters arbeitet mit dem Unterschwingungsverfahren der SinusDreieck-Modulation [80]. Auf Optimierungen des Steuersatzes wurde verzichtet, weil dessen
Einfluss auf den relativen Vergleich der Wechselrichterverluste bei unterschiedlicher
Drosselauslegung vernachlässigt wurde. Lediglich die Kompensation des Spannungsripples
mit der sechsfachen Netzfrequenz wurde berücksichtigt. Für die IGBTs und die
Freilaufdioden wurden einfache Halbleitermodelle verwendet. Dabei werden die Halbleiter in
109
Durchlassrichtung mit einer Spannungsquelle und einem Bahnwiderstand und in
Sperrrichtung mit einem Sperrwiderstand charakterisiert.
Der Sinusfilter wird als symmetrische Anordnung aus Induktivitäten und Kondensatoren
simuliert. Zusätzlich wird in Reihe zu der Induktivität ein Widerstand eingefügt. Dieser
Widerstand kann die Kupferverluste der Induktivität nachbilden. Parallel zur Induktivität wird
ein weiterer Widerstand eingefügt, mit dem die Eisenverluste der Induktivität modelliert
werden können. Da Verluste in der Filterdrossel für die zusätzliche Belastung der Halbleiter
irrelevant sind, werden sie in dieser Simulation vernachlässigt.
Der Motor als Last wird als dreiphasige Stromquelle nachgebildet. Dieses Modell besitzt im
Vergleich zu einem Motormodell den Vorteil, dass es wesentlich weniger Rechenzeit benötigt
und keine Anlaufvorgänge gerechnet werden müssen, bevor die Auswertung der
Halbleiterverluste im eingeschwungenen Zustand betrachtet werden kann.
Die Verlustberechnungen erfolgen in separaten Schaltkreisen für IGBT und Diode. Die
Verluste werden als Eingangsgröße für eine gesteuerte Stromquelle verwendet, die einen
Kondensator auflädt. Mit dieser Schaltung wird eine Aufsummierung aller Verluste über
einen betrachteten Zeitraum erreicht, so dass der Endwert der Kondensatorspannung
proportional zu der im Intervall anfallenden Verlustenergie ist.
Die als Eingangsgröße der Stromquelle verwendeten Verluste bestehen aus der Summe der
Durchlassverluste und der Schaltverluste. Die Durchlassverluste fallen als zeitkontinuierliche
Größe an den Halbleitern entsprechend der eingegebenen linearisierten Kennlinien an und
können unmittelbar in die Stromquelle eingespeist werden.
Die Schaltverlustenergie fällt hingegen als diskrete Größe zum jeweiligen Schaltzeitpunkt an.
Wird eine Schalthandlung festgestellt, so werden den Halbleitern in Abhängigkeit des
Wechselrichterausgangsstromes
Schaltverluste
zugeordnet.
Die
Höhe
der
Schaltverlustenergie, die bei einem entsprechenden Wechselrichterausgangsstrom anfällt,
wurde
zuvor
in
Doppelpulsversuchen
gemessen.
Sie
entsprechen
den
Verlustenergiekennlinien aus Abbildung 53.
Abhängig von der Stromrichtung des Ausgangsstromes und von der Polarität der
Schaltflanke des Ansteuersignals der IGBTs werden die Schaltverluste den einzelnen
Halbleiterbauelementen zugeordnet. Hierbei gilt bei folgender Notation der Stromrichtung für
die Bauelemente:
T1
D1
CZK
UZK
positive
Schaltflanke
IA
T2
D2
Abbildung 93: Halbbrücke des Wechselrichters
110
IA>0
Einschaltverluste T1
Ausschaltverluste D2
Ausschaltverluste T1
Einschaltverluste D2
positive Schaltflanke
negative Schaltflanke
IA<0
Einschaltverluste D1
Ausschaltverluste T2
Ausschaltverluste D1
Einschaltverluste T2
Tabelle 3: Zuordnung der Schaltverluste zu den Halbleitern
Als positive Schaltflanke wird hierbei der Wechsel des AC-Anschlusses von dem negativen
zum positiven Zwischenkreispotenzial definiert.
Die Einschaltverluste der Dioden werden i.a. zu null angenommen (vgl. Kap. 2.2.2.6). Bei der
Verwendung von SiC-Schottkydioden als Freilaufdioden wird deren Ausschaltverlustenergie
nach den Ergebnissen aus Kap. 2.2.2.5 unabhängig vom Laststrom, jedoch abhängig von
der verwendeten Diodenfläche berücksichtigt.
Mit der Simulation sollen die Halbleiterverluste in Abhängigkeit von dem gewählten
Ripplestrom bzw. der bezogenen Induktivität ermittelt werden. Allerdings sind für eine
Simulation die Vorgaben fester Größen, z.B. der Schaltfrequenz erforderlich, so dass die
Simulationsergebnisse zunächst nur für diese Schaltfrequenz gültig sind. Im vorliegenden
Fall wurde eine Schaltfrequenz von 16kHz verwendet. Direkt übertragbar auf andere
Schaltfrequenzen wären die Ergebnisse dann, wenn die Abhängigkeit der Durchlassverluste
und der Schaltverluste vom Ripplestrom identisch wäre. Da im vorliegenden Fall
insbesondere der Halbleiteraufwand für die SiC-Schottkydiode im Vordergrund steht, die nur
vernachlässigbare Schaltverluste verursacht, kann das Ergebnis auch auf andere
Schaltfrequenzen übertragen werden.
Mit geringerer Filterinduktivität steigt der Ripplestrom im Filter an. Deshalb steigen auch die
Verluste in den Halbleitern. Für den Einsatz von SiC-Freilaufdioden ist die Abhängigkeit der
Verluste der Halbleiterbauelemente von der Filterinduktivität dargestellt:
120
115
110
105
100
95
P/[%]
90
85
80
75
70
IGBT
65
60
55
SiC-Diode
50
45
40
0
1
2
3
4
5
6
7
8
9
10
11
L/Lref
Abbildung 94: Halbleiterverluste in Abhängigkeit der Filterinduktivität
111
12
13
14
15
Aus Abbildung 94 ist zu erkennen, dass die Verluste der Leistungshalbleiter mit steigender
Filterinduktivität beachtlich abnehmen. Der durch den Sinusfilter zusätzlich hervorgerufene
Ripplestrom trägt bei kleiner Filterinduktivität stark zu den Halbleiterverlusten bei. Bei großer
Filterinduktivität endet dieser Effekt in einem Grenzwert, weil dann der Filterstrom gegenüber
dem Grundschwingungsstrom unbedeutend wird.
Die Abszisse aus Abbildung 94 ist identisch zu der Abszisse in Abbildung 85 zu verstehen.
Der Wert 1 bezeichnet eine Filterdrossel, die zu einem Ripplestrom führt, dessen
Scheitelwert identisch dem Scheitelwert der Grundschwingung des Laststroms ist. Diese
Filterdrossel besitzt den minimalen Energiegehalt und lässt somit den geringsten
Kostenaufwand für die Drossel erwarten. Auf die Halbleiterverluste bei dieser
Filterinduktivität sind die Werte der Ordinate bezogen. Ausgehend von diesem
Auslegungspunkt können die Halbleiterverluste jedoch für den IGBT und die SiCSchottkydiode durch Reduzierung des Ripplestroms noch auf ca. 55% abgesenkt werden.
Damit können die Halbleiterflächen und somit die Kosten für die Halbleiter gesenkt werden.
3.2.3.2 Ermittlung des kostenoptimalen Ripplestromes
Letztendlich ist für die Wahl des optimalen Ripplestromes die Summe der Kosten für
Halbleiter und Drossel entscheidend. Ein solches Optimum kann aus Abbildung 85 und
Abbildung 94 abgeleitet werden.
Bezeichnet man in Abbildung 85 die Drosselkosten bei der Referenzinduktivität Lref mit KDref
und geht man davon aus, dass sich die Kosten der Drossel gemäß deren Energieinhalt
ändern, so gilt für die Kosten der Drossel als Funktion der Induktivität nach Abbildung 85 und
Gl. (81):
KD( L) = KDref ⋅
L
Lref
L
⎛
⎜⎜1 + ref
L
⎝
4
⎞
⎟⎟
⎠
2
(90)
Für die Halbleiterkosten kann ein ähnlicher Ansatz gewählt werden, indem die Verlustkurven
aus Abbildung 94 durch eine analytische Funktion angenähert werden. Um daraus eine
erforderliche Halbleiterfläche zu berechnen, sind im Prinzip thermische Simulationen
vergleichbar zu Kap. 2.3.3 erforderlich. Für eine grobe Abschätzung können jedoch folgende
grundsätzliche Überlegungen herangezogen werden:
¾ Schaltverluste sind in erster Nährung unabhängig von der Halbleiterfläche.
Tendenziell nehmen sie mit steigender Halbleiterfläche leicht zu, weil die im IGBT
gespeicherte Ladung mit der Halbleiterfläche ansteigt (vgl. Kap. 2.3.3) und somit der
Verlustanteil zunimmt, der durch Speicherladungen verursacht wird. Für die SiCSchottkydiode sind sowohl die Schaltverluste als auch deren Abhängigkeit von der
Halbleiterfläche sehr gering (vgl. Kap. 2.2.2.5).
¾ Durchlassverluste aufgrund von Schwellenspannungen sind unabhängig von der
Halbleiterfläche.
¾ Durchlassverluste aufgrund des ohmschen Anteils der Durchlasskennlinie nehmen
mit steigender Halbleiterfläche linear ab, weil der ohmsche Widerstand linear
abnimmt.
In Summe kann aus diesen Überlegungen stark vereinfacht abgeleitet werden, dass die
Verluste in erster Näherung unabhängig von der Halbleiterfläche sind. Damit ist der
Halbleiteraufwand den Verlusten proportional, um den Temperaturhub am Halbleiter
112
konstant zu halten. Bezeichnet man die Halbleiterkosten KH bei der Induktivität Lref als KHref,
so gilt gemäß der Ausgleichskurve aus Abbildung 94:
KH ( L) = KH ref
⎛
⎜
45
⎜
55
+
⎜
L 2
(
)
⎜⎜
L
ref
⋅⎝
100
⎞
⎟
⎟
⎟
⎟⎟
⎠
(91)
Die Ausgleichskurve für die Hableiter wurde stärker an die Verlustkurve der SiC-Diode als an
den Si-IGBT angepasst, weil die SiC-Diode für die Kosten des Moduls dominant ist.
Für die Gesamtkosten gilt somit:
Kges = KD + KH = KDref
Lref
L ⎛
• ⎜⎜1 +
Lref ⎝
L
⋅
4
⎞
⎟⎟
⎠
2
+ KH ref
⎛
⎜
45
⎜
⎜ 55 + L 2
(
)
⎜⎜
Lref
⎝
⋅
100
⎞
⎟
⎟
⎟
⎟⎟
⎠
(92)
Das Minimum aus Gl. (92) liefert den kostenoptimalen auf die Referenzinduktivität
bezogenen Induktivitätswert. Aus Abbildung 85 kann daraus der kostenoptimale Ripplestrom
abgelesen werden. Das Ergebnis hängt von dem Verhältnis von Drossel- und
Halbleiterkosten bei dem Referenzwert ab, wobei grundsätzlich bei steigender Induktivität die
Drosselkosten und bei geringen Induktivitätswerten die Halbleiterkosten dominieren. Für
unterschiedliche Verhältnisse von KHref/KDref = 1, 10 und 100 können dann die normierten
Kosten aufgetragen werden:
3
3
2.5
Kges1
L
Kges10
L
2
Kges100
L
1.5
1
0.8
0
1
2
3
4
5
6
7
8
9
10
L
0.1
11
12
13
14
15
15
Lref
Abbildung 95: Normierte Gesamtkosten für Drossel und Halbleiter
Aus Abbildung 95 ist zu erkennen, dass bei Kostengleichheit von Drossel und Halbleiter (rote
Kurve) im Referenzpunkt das Optimum knapp unterhalb der doppelten Referenzinduktivität
113
liegt. Mit zunehmendem Gewicht des Halbleiteraufwands verändert sich das Optimum zu
höheren Induktivitätswerten. Bei der Bewertung der Kostenverhältnisse im Referenzpunkt sei
daran erinnert, dass dieser für den Drosselaufwand das Optimum darstellt, während die
Halbleiter in diesem Punkt stark überdimensioniert sind.
Für den Demonstrator wurde eine Drosselauslegung mit
L
= 7 gewählt. Für den
Lref
Ripplestrom geht aus Abbildung 85 damit hervor, dass sein Scheitelwert ca. 15% des
Scheitelwertes des Grundschwingungsstromes beträgt.
3.2.4 Auswahl der Schaltfrequenz
Nach der Festlegung auf einen gewünschten Ripplestrom kann die erforderliche Induktivität
der Filterdrossel nach Gl. (85) in Abhängigkeit von der Dauer der Modulationsperiode
bestimmt werden. Die Modulationsperiode bzw. Schaltfrequenz kann frei eingestellt werden.
Die Auswirkungen der Schaltfrequenz auf den Flächenbedarf der Leistungshalbleiter wurde
in Kapitel 2.3 bereits ausführlich diskutiert. Mit zunehmender Schaltfrequenz steigt der
Halbleiterbedarf an, wobei dieser Anstieg beim Einsatz von SiC-Bauelementen deutlich
geringer ausfällt als bei Si-Bauelementen.
Der umgekehrte Effekt stellt sich bei dem Aufwand für die Filterdrossel dar, weil nach Gl.
(85) bei konstantem Ripplestrom die erforderliche Induktivität mit dem Kehrwert der
Schaltfrequenz abnimmt. Gemäß Gl. (80) sollten somit auch das Volumen und die Kosten für
die Filterdrossel umgekehrt proportional zu der Schaltfrequenz sein. Dies ist jedoch in der
einfachen Form nicht der Fall. Die wesentlichen Gründe hierfür sind:
a) Mit steigender Frequenz nehmen bei konstantem Ripplestrom und unverändertem
Kernmaterial die Kernverluste der Drossel zu (Hystereseverluste linear mit der
Frequenz, Wirbelstromverluste quadratisch zur Frequenz). Erhöhte Verluste erfordern
jedoch eine vergrößerte Oberfläche zur Kühlung und damit ein vergrößertes Volumen
und erhöhte Kosten. Deshalb müssen mit erhöhter Frequenz andere Kernmaterialien
eingesetzt werden, die geringere Kernverluste verursachen. Der Nachteil dieser HFtauglichen Kernmaterialien besteht darin, dass sie nur eine geringere Flussdichte
erlauben ([32], [94]), was sich in Gl. (80) niederschlägt. Ein Vergleich verschiedener
Kernmaterialien bzgl. typischer Betriebsfrequenz und Sättigungsflussdichte ist in
Tabelle 4 dargestellt.
Material
Blech
Eisenpulver
Ferrit
Typ. Sättigungsflussdichte/[T]
1,7
1,2
0,4
Typ. Betriebsfrequenz/[kHz]
0-6
0 - 60
> 60
Tabelle 4: Vergleich unterschiedlicher Kernmaterialien bzgl. ihrer Sättigungsflussdichte und
typ. Betriebsfrequenz
b) Der Umrichter mit sinusförmiger Ausgangsspannung soll in einem Leistungsbereich
von 3KW bis 55kW realisierbar sein. Insbesondere für die hohe Leistung existieren
aber heute keine Standardkerne mit HF-optimierten Materialien, mit denen Drosseln
hergestellt werden können. Für diese Lösungen müssen Kerne verwendet werden,
die nur in sehr geringer Stückzahl existieren und deshalb hohe Kosten verursachen.
114
Letztendlich ist es erforderlich, verschiedene Drosselvarianten miteinander zu vergleichen
und daraus ein Gesamtoptimum unter Berücksichtigung des Halbleiteraufwands abzuleiten.
Zu diesem Zweck wurden verschiedene Drosseln verschiedener Hersteller einem Test in
einem 2-Quadranten-Steller unterzogen. Das Schaltbild und der zugehörige Stromverlauf
sind in Abbildung 35 und in Abbildung 36 bereits erläutert worden. Die Drosseln sind
abhängig von dem jeweiligen Kernmaterial für unterschiedliche Schaltfrequenzen ausgelegt.
Als Scheitelwert des Ripplestroms wurde ein Wert von 15% der Amplitude des
Grundschwingungsstromes eingestellt. Die zulässige Drosselerwärmung betrug bei dem
Test 40K bei forcierter Kühlung. Aus Gründen der Vergleichbarkeit wurde diese Grenze für
alle Versuche unabhängig von der Curie-Temperatur des Kernmaterials beibehalten.
Als Ergebnis dieses Tests ergibt sich für alle Drosseln eine maximale Stromtragfähigkeit.
Anhand von Beobachtungen des Stromverlaufs auf dem Oszilloskop kann sichergestellt
werden, dass keine unzulässigen Sättigungseffekte in der Drossel auftreten. Das Volumen
der einzelnen Drosseln, umgerechnet auf eine dreiphasige Lösung, ist in Abbildung 96
dargestellt:
3
Blech
(4kHz)
Volumen/[dm 3]
2.5
2
Ferrit
(64kHz)
1.5
KoolMµ
(64kHz)
1
0.5
Eisenpulver
(16kHz)
0
0
5
10
15
20
25
30
35
40
45
50
IMotor/[A]
Abbildung 96: Drosselvolumen als Funktion des Motorstromes bei unterschiedlicher
Schaltfrequenz
Die Datenbasis für Abbildung 96 bilden reale Drosselauslegungen unter Verwendung heute
verfügbarer Kern- und Drosselbauformen. Die einzelnen Datenwerte sind in den Kurven
hervorgehoben und durch lineare Interpolation miteinander verbunden. Die Kopplung an real
existierende Kernbauformen erklären die Unstetigkeiten in den gezeigten Kurven, die auch
bei der realen Definition einer Umrichterreihe auftreten.
Die Verwendung geblechter Eisenkerne ist heute bei Sinusfiltern für Umrichter Stand der
Technik. Sie sind allgemein verfügbar. Das hierfür erforderliche Volumen ist in Abhängigkeit
des Motorstromes in Abbildung 96 dargestellt und kann als Referenzkurve verwendet
werden. Die Auslegung gilt für eine Schaltfrequenz von 4kHz, die für Umrichter am 400VNetz standardmäßig heute verwendet wird. Für Umrichter am 690V-Netz stellt sie bereits
eine erhöhte Schaltfrequenz dar, weil diese i.a. mit einer Schaltfrequenz von 2kHz betrieben
werden. Bei 2kHz würde das erforderliche Drosselvolumen noch weiter ansteigen, weil bei
gleichem Ripplestrom die Induktivität vergrößert werden müsste.
115
Erhöht man die Schaltfrequenz auf 16kHz, so sind geblechte Eisenkerne aufgrund der hohen
Eisenverluste nicht mehr einsetzbar. In diesem Frequenzbereich können Drosseln aus
Eisenpulver eingesetzt werden [4]. Kerne aus Eisenpulver werden in einem Sinterprozess
hergestellt und bestehen aus einem Verbund kleiner ferromagnetischer Partikel und einem
nicht ferromagnetischen Bindemittel. Statt eines ausgeprägten Luftspaltes besitzen diese
Materialien einen verteilten Luftspalt, der aus den Zwischenräumen zwischen den
ferromagnetischen Teilchen besteht. Der Luftspalt ist erforderlich, um eine Sättigung des
Kernmaterials zu verhindern. Die Luftspaltverluste sind bei verteiltem Luftspalt kleiner als bei
konzentriertem Luftspalt, weil bei einem konzentrierten Luftspalt Streufeldlinien in die
Wicklung der Drossel eindringen und dort Wirbelstromverluste verursachen.
Mit der Verwendung des Eisenpulverkernes kann die Baugröße der Drossel im Vergleich zu
dem geblechten Kern etwa um den Faktor 4 reduziert werden. Dies entspricht dem
Verhältnis, in dem die Schaltfrequenz erhöht wurde. Die Induktivität der Drossel mit dem
Eisenpulverkern ist um den Faktor 4 gegenüber dem Blechkern reduziert, so dass in beiden
Drosseln etwa der gleiche Ripplestrom zu erwarten ist.
Für sehr kleine Leistungen im Bereich unter 5kW fällt die Volumenreduzierung geringer als
der Faktor 4 aus, es ist nur ein Faktor 2 zu beobachten. Ursache hierfür ist die Tatsache,
dass die Eisenpulverkerne heute standardmäßig in hohen Stückzahlen für aktive
Netzstromrichter verwendet werden, die ebenfalls mit einer Schaltfrequenz zwischen 8kHz
und 12kHz verwendet werden. Diese aktiven Netzstromrichter werden mit einer Leistung von
10kW und höher hergestellt. Für Leistungen unter 5kW existieren deshalb keine optimierten
Kernformen, so dass die Vorteile in diesem Leistungsbereich nicht vollständig ausgenutzt
werden können.
Bei einer weiteren Erhöhung der Schaltfrequenz des Umrichters auf 64kHz sind auch
Eisenpulverkerne aufgrund der Kernverluste nicht mehr vorteilhaft. In diesem Fall bietet der
Einsatz von KoolMµ oder Ferrit die beste Performance [132]. KoolMµ ist ebenfalls ein
Pulverkernmaterial aus einer Al, Si und Fe-Legierung und zeigt gegenüber herkömmlichem
Eisenpulver reduzierte Kernverluste. Für Ferrit ist eine Schaltfrequenz von 64kHz die untere
Grenze des vorteilhaften Einsatzbereiches, das Material bietet vor allem für noch höhere
Schaltfrequenzen Vorteile.
Aus Abbildung 96 ist ersichtlich, dass der Übergang von 16kHz auf 64kHz keinen besonders
großen Vorteil bei der Volumenreduzierung der Drosseln bietet. Vorteile ergeben sich im
Besonderen bei sehr kleinen Leistungen. Auch hier ist die Ursache, dass im
Leistungsbereich vieler Kilowatt keine optimierten Kernformen aus Ferrit oder KoolMµ
existieren. Die Drosseln müssen in diesem Bereich aus Kernbausteinen in U-Form oder IForm zusammengesetzt werden. Bezüglich der Kosten sind diese Drosseln nicht attraktiv,
weil sie keine kostengünstigen Standardkerne verwenden können. Bei kleiner Leistung
existieren Standardkerne aus Ferrit oder KoolMµ, dort ergibt sich ein Vorteil gegenüber
standardmäßigem Eisenpulver. Allerdings ist zu berücksichtigen, dass bei der hohen
Schaltfrequenz die Halbleiterverluste deutlich zunehmen (s. Abbildung 56 und Abbildung 58).
Bei Betrachtung des gesamten Leistungsbereiches ergibt sich für das 690VUmrichterleistungsteil ein Optimum in dem Aufwand für Sinusfilterdrossel und
Leistungshalbleiter bei einer Schaltfrequenz von 16kHz. Für den Demonstratorumrichter mit
einer Leistung von 18,5kW ergibt sich für die Filterdrossel ein Induktivitätswert von 0,7mH.
Neben dem Kostenoptimum als Auslegungskriterium existiert noch eine weitere Motivation,
die Induktivität der Sinusfilterdrossel möglichst klein zu wählen. Neben dem Ripplestrom, der
durch die Sinusfilterdrossel begrenzt werden soll, erzeugt auch der Grundschwingungsstrom
einen Spannungsabfall an der Drossel. Zwar ist dieser aufgrund seiner niedrigen Frequenz
so gering, dass er in Kap. 3.1 für die Beschreibung der Ausgangsspannungen in erster
116
Näherung vernachlässigt wurde. Für die Gesamtperformance eines Umrichters spielt er
dennoch eine Rolle, weil die an der Drossel abfallende grundfrequente Spannung vektoriell
von der Grundschwingung der Umrichtrausgangsspannung zu subtrahieren ist und somit am
Motor nicht zur Verfügung steht, wie aus dem Ersatzschaltbild in Abbildung 80 zu erkennen
ist. Da ein Motor für den Betrieb an der vollen Höhe der Netzspannung ausgelegt ist, kann
seine Leistungsfähigkeit bei reduzierter Spannung nicht vollständig genutzt werden. Dieser
Effekt nimmt linear mit der Induktivität der Sinusfilterdrossel zu. Da die Induktivität der
Drossel wiederum gemäß Gl. (85) umgekehrt proportional zur Schaltfrequenz ist, ist auch der
grundfrequente Spannungsabfall an der Sinusfilterdrossel umgekehrt proportional zur
Schaltfrequenz. Der Motor kann bei einem Sinusfilter für hohe Schaltfrequenz in seiner
Leistung besser ausgenutzt werden.
3.3 Auslegung Kondensator
3.3.1 Dimensionierung der Filtereckfrequenz
Ist die Induktivität der Sinusfilterdrossel festgelegt, so kann durch die Wahl der Filterkapazität
die Eckfrequenz des Sinusfilters festgelegt werden. Obere Begrenzung der Eckfrequenz ist
hierbei in der Motorspannung die zulässige Amplitude der Spannungsanteile mit
Schaltfrequenz und deren Vielfachen. Bei der in Abbildung 76 dargestellten Topologie des
symmetrischen LC-Sinusfilters mit Drossel und Kondensator ist die Spannung an einem
Filterkondensator identisch zu der Strangspannung am Motor. Der Betrag der
Übertragungsfunktion des ungedämpften Sinusfilters zwischen Kondensatorspannung und
symmetrischer Wechselrichterausgangsspannung berechnet sich mit dem Ersatzschaltbild
aus Abbildung 82 zu:
G (ω ) =
U CW (ω )
1
=
U WD (ω ) 1 − ω 2 LC
(93)
mit der Resonanzfrequenz
ω res =
1
(94)
LC
Soll bei einer bestimmten Frequenz ω1 eine definierte Amplitude G(ω1) <1 erreicht werden,
so kann daraus die minimal erforderliche Resonanzfrequenz des Filters errechnet werden.
Als Bedingung für die Auswahl der Resonanzfrequenz gilt somit:
ω res ≤ ω1
G (ω )
1 + G (ω )
(95)
Für den 690V-Demonstratorumrichter soll beispielsweise festgelegt werden, dass die
Spannungsamplitude bei der Schaltfrequenz von 16kHz kleiner 2,5% der
Zwischenkreisspannung sein soll. Aus Abbildung 79 ist ersichtlich, dass die Seitenbänder
der Schaltfrequenz in der symmetrischen Ausgangsspannung maximal 11% der
Zwischenkreisspannung betragen können. Die Übertragungsfunktion G(w) des Filters muss
somit bei dieser Frequenz etwa einen Faktor 4 - 5 an Reduzierung der Amplitude bewirken.
Nach Gl. (95) kann somit eine erforderliche Resonanzfrequenz von ca. 6,3kHz berechnet
werden.
117
20
100
Grundfrequenz
Schaltfrequenz
10
Betrag
Frequenz
1
0.1
0.01
0.01
100
100
1 .10
3
Frequenz
1 .10
4
1 .10
5
1 .10
5
Abbildung 97: Übertragungsfunktion des ungedämpften Filters für den Demonstrator
Die erforderliche Reduzierung der schaltfrequenten Spannungsanteile liefert die obere
Grenze der zulässigen Filterresonanzfrequenz. Die untere zulässige Grenze ergibt sich aus
der Forderung möglichst kleiner und somit kostengünstiger Bauteile, so dass sich eine reale
Filterauslegung an der oberen zulässigen Grenzfrequenz orientieren wird. Darüber hinaus ist
darauf zu achten, dass durch eine niedrige Filtereckfrequenz eine Filteranregung durch die
Grundschwingung und deren Harmonische (5., 7., 11., 13.) möglich ist. Deshalb ist von der
maximal zulässigen Grundschwingungsfrequenz ein Abstand einzuhalten, der eine
Filteranregung ausschließt. Im Fall des Demonstratorumrichters beträgt die maximal
zulässige Umrichterausgangsfrequenz 200Hz.
Für den Demonstratorumrichter wurde bei einer Ausgangsleistung von 18,5kW und einer
Filterdrossel von 0,7mH eine Filterkapazität von 1µF in Sternschaltung berechnet. Mit diesen
Werten ergibt sich eine Resonanzfrequenz von ca. 6kHz. Für den Umrichter ergeben sich
damit am Wechselrichterausgang und am Umrichterausgang folgende Spannungen:
Filterausgangsspannung
Filtereingangsspannung
kV
1.2
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2
0
5
10
15
20
25
30
35
40
ms
Abbildung 98: Verkettete Spannung am Wechselrichterausgang (magenta) und am
Filterausgang (blau) bei Ausgangsfrequenz 50Hz, 100% Aussteuerung, leerlaufender Umrichter
118
Optisch ist die Filterung der Ausgangsspannung gut zu erkennen. In der gepulsten
Spannung ist im Maximum der Grundschwingungsamplitude bereits ein Bereich zu
erkennen, in dem Pulse aufgrund von Mindestzeiten nicht realisiert werden können. Der
Umrichter befindet sich dabei im Übersteuerungsbereich, weil die Zwischenkreisspannung
mit dem charakteristischen 300Hz-Ripple der F3E-Gleichrichterschaltung nicht mehr zu
jedem Zeitpunkt die erforderliche Spannung zur Verfügung stellen kann. Durch diesen
Zustand werden zusätzliche Oberschwingungen erzeugt. Der Betriebspunkt wurde trotzdem
als auslegungsrelevant ausgewählt, weil nach Abbildung 79 bei der Aussteuerung von 100%
die höchsten Frequenzanteile bei den Seitenbändern der Schaltfrequenz zu erwarten sind.
Die zusätzlichen Oberschwingungen durch die Übersteuerung können für den Filter nur eine
zusätzliche Anregung darstellen, so dass der betrachtete Arbeitspunkt einen worst case
darstellt.
Zur detaillierten Bewertung der Filtereigenschaften werden die Spektren der beiden
Spannungen vor und nach dem Sinusfilter verglichen:
Fil.b
V
WR.b
1·103
1·102
1·101
1·100
1·10-1
0
10
20
30
40
50
60
70
80
90 100
kHz
Abbildung 99: Spektrum der gepulsten (magenta) und der gefilterten (blau) verketteten
Ausgangsspannung (Scheitelwerte), 50Hz, 100% Aussteuerung, leerlaufender Umrichter
Wie zu erwarten, nehmen die Spektralanteile der Seitenbänder mit höheren Vielfachen der
Schaltfrequenz ab. Da die Amplitudenreduzierung des Filters mit steigender Frequenz um
theoretisch 40dB pro Dekade zunimmt, ist der Frequenzanteil der Seitenbänder der
einfachen Schaltfrequenz in der Ausgangsspannung als Oberschwingung dominant. Die
Amplitude der Seitenbänder der einfachen Schaltfrequenz beträgt ca. 175V.In Abbildung 79
119
wurden 11% der Zwischenkreisspannung als Amplitude der Phasenspannung errechnet. In
Abbildung 99 ist die verkettete Spannung dargestellt, bei einer Zwischenkreisspannung von
1000V ist deshalb mit einer Amplitude von 190V zu rechnen, was leicht über der
gemessenen Spannung liegt. In der gefilterten Ausgangsspannung verbleibt ein
Spektralanteil von ca. 34V. Damit erreicht der Filter auch in der Messung den Faktor 5 in der
Abschwächung der Spektralanteile, der sich aus Abbildung 97 rechnerisch ergibt.
3.3.2 Dämpfung des Filters
3.3.2.1 Bestimmung der existierenden Dämpfung
Bei der Resonanzfrequenz besitzt die ungedämpfte Übertragungsfunktion des Filters eine
unendlich hohe Verstärkung. Da in der Realität kleine Anregungen bei der Filterresonanz
nicht vollständig ausgeschlossen werden können, ist eine zu definierende Dämpfung des
Filters erforderlich.
Da der Filter aus realen Bauteilen besteht, ist die unendlich hohe Verstärkung bei der
Resonanzfrequenz des Filters nicht gegeben. Um die bestehende Verstärkung des Filters
bei Resonanzfrequenz zu ermitteln, wurde zunächst die anregende Spannungsamplitude bei
der Resonanzfrequenz des Filters durch eine Frequenzanalyse der gepulsten
Wechselrichterausgangsspannung gemessen und anschließend mit dem Spektralanteil in
der Filterausgangsspannung verglichen.
Fil.b
V
WR.b
1·103
1·102
1·101
1·100
1·10-1
0
2
4
6
8
10
12
14
16
18
20
kHz
Abbildung 100: Spektrum der gemessenen Wechselrichterausgangsspannung (magenta) und
der Filterausgangsspannung (blau) bei 50Hz Ausgangsfrequenz und leerlaufendem Umrichter
120
Bei der Filterresonanzfrequenz von ca. 6kHz beträgt die anregende Amplitude etwa 0,8V. In
der Filterausführung als reine LC-Kombination mit realen Bauelementen ergibt sich in der
Filterausgangsspannung bei der Resonanzfrequenz eine Amplitude von ca. 5V. Die
Verstärkung bei der Resonanzüberhöhung beträgt somit etwa den Faktor 6. Dies wird für
den Demonstrator als unkritisch betrachtet, so dass auf den Einsatz expliziter
Dämpfungselemente verzichtet wird.
Die Dämpfungseigenschaften des Filters werden zum überwiegenden Teil durch die Verluste
in der Filterdrossel bewirkt.
3.3.2.2 Bestimmung der frequenzabhängigen Drosselverluste
Somit existieren für die Dämpfung des Filters frequenzunabhängige Kupferverluste und
frequenzabhängige Hysterese- und Wirbelstromverluste. Durch zwei Messungen können
diese Verlustanteile bestimmt werden:
In einem ersten Versuch wird die Filterdrossel mit einem Gleichstrom aus einem Netzgerät
bestromt. Dieser Versuch bildet den Verlustanteil in der Drossel nach, der durch den
grundfrequenten Motorstrom hervorgerufen wird. Dabei wird angenommen, dass dessen
Grundfrequenz so gering ist, dass sie nahezu keine Eisenverluste verursacht und somit der
grundfrequente Strom durch einen Gleichstrom ersetzt werden kann. Im Fall des 18,5kW
Demonstratorumrichters führt der DC-Umrichternennstrom von I1=23A zu einer
Temperaturerhöhung der Filterdrossel von ∆T1= 7,1K. Die Drosseln befinden sich bei diesem
Versuch im Originaleinbauplatz im Umrichter und werden mit forcierter Luftkühlung identisch
zum Umrichterbetrieb gekühlt.
In einem zweiten Versuch wird der Umrichter bei maximaler Aussteuerung und Nennlast
betrieben. In diesem Fall stellt sich ein Filterdrosselstrom von ca. I2=23,8A ein. Bei diesem
Versuch ergibt sich eine Temperaturerhöhung von 63,8K. Hierbei ist zu berücksichtigen,
dass die Vorwärmung der Kühlluft aufgrund der taktenden IGBTs gemäß Kap. 3.2.2.4 14K
beträgt, so dass die effektive Temperaturerhöhung ∆T2= 49,8k beträgt.
Die Temperaturerhöhung aufgrund von Kupferverlusten kann in diesem zweiten Versuch bei
Vernachlässigung des Skineffektes aus einem Vergleich mit dem Gleichstromversuch
berechnet werden kann:
ΔT2CU
⎛I
= ΔT1 ⎜⎜ 2
⎝ I1
⎞
⎟⎟
⎠
2
(96)
Für die durch Kupferverluste bedingte Temperaturerhöhung aus dem zweiten Versuch ergibt
sich ein Wert von 7,6K. In Summe ergeben sich somit Kupferverluste von ca. 13% und
Eisenverluste von ca. 87%. Die Dämpfung in der Übertragungscharakteristik wird im Fall des
Demonstrators somit vorwiegend über Kernverluste der Drossel erzeugt. Aus Messungen
des thermischen Widerstandes der Sinusfilterdrossel ergibt sich für den Demonstrator aus
der gemessenen Temperaturerhöhung eine Verlustleistung von 33W pro Drossel bei
Nennstrom.
121
3.3.2.3 Auswirkungen der Dämpfung und des Motors auf die
Übertragungscharakteristik
Um die vorwiegend aus Hysterese- und Wirbelstromverlusten bestehende Dämpfung im
elektrischen Ersatzschaltbild des Filters nachzubilden, wird deshalb ein Ersatzwiderstand
parallel zu der Filterdrossel eingeführt. Die Der Betrag der Übertragungsfunktion beträgt nun
unter Berücksichtigung dieser Dämpfung:
G d (ω ) =
1
ω LF RFe C F
1−
RFe + jωLF
(97)
2
Bei den verwendeten Bauteilen für den Demonstrator mit einer Induktivität von 0,7mH und
einer Filterkapazität von 1µF wird für die Realisierung der gemessenen Begrenzung der
Resonanzüberhöhung auf den Faktor 6 ein Ersatzwiderstand RFe von ca. 160Ω benötigt. Für
die Übertragung auf reale Bauteile sei darauf hingewiesen, dass dieser Ersatzwiderstand
eine frequenzabhängige Größe repräsentiert.
In Abbildung 100 ist die Filterausgangsspannung ohne angeschlossenen Motor dargestellt.
In Kap. 3.1 wurde eine Zerlegung des Umrichterausgangs in grundfrequente und
hochfrequente Größen vorgenommen, wodurch der Einfluss des Motors auf die
Filtereigenschaften vernachlässigt wurde. Um zu überprüfen, ob diese Vereinfachung
zulässig ist, sollen an dieser Stelle die Ausgangsspannungen des Umrichters mit und ohne
angeschlossenen
Motor
miteinander
verglichen
werden.
Nimmt
man
eine
Motorstreuinduktivität von 20% an, so entspricht dies im Fall des Demonstrators einer
Induktivität LM von 11mH. Die Berücksichtigung des Motors ergibt folgendes Ersatzschaltbild
LF
LM
RFe
UWD
CF
UiM
UCF
Abbildung 101: Einphasiges Ersatzschaltbild des Sinusfilters unter Berücksichtigung von
Motor und Dämpfung
mit der zugehörigen Übertragungsfunktion:
1
G dM ( w ) =
w 2 LF RFe LM +
1−
(98)
LF RFe
CF
LM
(RFe + jwLF )
CF
Die Übertragungsfunktionen von Gl. (97) und Gl. (98) sind in Abbildung 102 dargestellt:
122
20
100
Grundfrequenz
Schaltfrequenz
10
Gd
Frequenz
GdM
Frequenz
1
0.1
0.01 0.01
1 .10
100
100
3
4
5
1 .10
100000
1 .10
Frequenz
Abbildung 102: Übertragungsfunktion des Sinusfilters unter Berücksichtigung von Dämpfung
(blau) sowie unter Berücksichtigung von Dämpfung und Motor (rot)
Die Änderung in der Übertragungsfunktion durch Berücksichtigung des Motors ist gering.
Daraus wird die Schlussfolgerung gezogen, dass die Vernachlässigung des Motors für die
Übertragungsfunktion des Sinusfilters zulässig ist. Durch die Berücksichtigung des Motors
wird die Resonanzfrequenz leicht nach oben verschoben, die Resonanzüberhöhung ist
etwas geringer. Bei der Schaltfrequenz ist die Abschwächung der Amplituden nahezu
identisch, tendenziell etwas schwächer bei der Berücksichtigung des Motors.
ohne_Motor.b
mit_Motor.b
V
1·103
1·102
1·101
1·100
1·10-1
0
2
4
6
8
10
12
14
16
18
20
kHz
Abbildung 103: Spektrum der gemessenen Ausgangsspannung ohne (blau) und mit (magenta)
leerlaufendem 15kW Motor
123
Die Messungen am Demonstrator bestätigen diese Berechnungen. Die Unterschiede in den
Spektren der Umrichterausgangsspannung mit und ohne Motor sind gering. Die blaue Kurve
in Abbildung 103 ist identisch zu Abbildung 100 und wird als Referenz verwendet. In der
Messung mit angeschlossenem, leerlaufendem 15kW Motor ist die Resonanzfrequenz leicht
erhöht und die Resonanzüberhöhung leicht reduziert. Die Seitenbänder der Schaltfrequenz
zeigen einen leicht erhöhten Spektralanteil.
3.3.3 Selbsterregung
Ein weiteres Phänomen, das bei der Dimensionierung des Filterkondensators zu
berücksichtigen ist, ist die Grenze zur Selbsterregung des Motors [2].
Ein rotierender Asynchronmotor benötigt an seinen Klemmen einen Blindstrom für die
Aufmagnetisierung. Beim Betrieb am Netz wird dieser Blindstrom dem Netz entnommen.
Re
US
IS
M
Im
Abbildung 104: Kreisdiagramm für den Ständerstrom einer Asynchronmaschine nach Heyland
bzw. Osanna ohne Berücksichtigung des Ständerwiderstandes
Abbildung 104 zeigt die Ortskurve für den Ständerstrom eines Asynchronmotors bei
gegebener Ständerspannung und Ständerfrequenz [3]. Die Kreislinie bezeichnet die
möglichen Arbeitspunkte für den Ständerstrom. Bei allen Punkten mit positiver Ordinate, d.h.
positivem Realteil, wird dem angeschlossenen Netz Wirkleistung entnommen, bei negativem
Realteil arbeitet die Asynchronmaschine als Generator. Da kein Betriebspunkt existiert, bei
dem der Imaginärteil des Ständerstromes zu null wird, geht aus Abbildung 104 hervor, dass
für alle Betriebpunkte ein Blindstrom aus dem Netz erforderlich ist.
Bei Betrieb des Asynchronmotors an einem Frequenzumrichter muss dieser den
erforderlichen Blindstrom bereitstellen. Stellt im Umkehrschluss der Frequenzumrichter den
Blindstrom nicht zur Verfügung, ist eine Aufmagnetisierung des Motors nicht möglich.
Besitzt der Frequenzumrichter motorseitig einen Kondensator, so kann dieser unter
Umständen einen Blindstrom für den Motor liefern, ohne dass der Frequenzumrichter
betrieben wird. Dieser Betriebszustand wird in der Literatur als Selbsterregung bezeichnet
[33]. Er wird hauptsächlich in der Anwendung der Asynchronmaschine als Generator für
Inselnetze genutzt, da ein Inselnetz den erforderlichen Blindstrom nicht zur Verfügung stellen
kann. In diesem Fall wird der Asynchronmaschine ein parallel angeschlossener Kondensator
vorgeschaltet, der dadurch auf sehr einfache Art die Funktion einer Erregereinrichtung
übernimmt.
124
Bei dem Betrieb am Frequenzumrichter ist dieses Verhalten jedoch unerwünscht, weil bei
abgeschaltetem Frequenzumrichter der Motor keine eigenständigen Betriebspunkte
annehmen soll. Deshalb besteht am Frequenzumrichter die Forderung, die Selbsterregung
durch dementsprechende Dimensionierung der Bauelemente zu vermeiden.
LF
iµ
iC
CF
WR
US
LS1
L’S2
Lh
R’2
s
Abbildung 105: Einphasiges Ersatzschaltbild von Umrichterausgangsstufe und
Asynchronmotor
Abbildung 105 zeigt das einphasige Ersatzschaltbild des Umrichterausgangs mit Sinusfilter
sowie das einphasige Ersatzschaltbild der Asynchronmaschine. Der Umrichter wird im
Leerlauf betrachtet (s=0), so dass im Rotor des Motors kein Strom fließt. Der Wechselrichter
des Umrichters ist gesperrt, so dass in der Filterdrossel auch kein Strom fließt, solange die
Spannung US kleiner als die Zwischenkreisspannung ist. Ein Strom kann somit nur im
Ständer der Asynchronmaschine und in dem Filterkondensator fließen. Damit sich ein
stabiler Betriebspunkt einstellen kann, muss gelten:
− i c = i µ = − jwC U S =
US
jw ( LS 1 + Lh )
(99)
Der Magnetisierungsstrom der Asynchronmaschine kann als Funktion der Ständerspannung
gemessen werden. In Abbildung 106 ist der typische Verlauf eines Magnetisierungsstromes
bei einer gewählten Frequenz dargestellt:
U
C3
C2
C1
U1
Magnetisierungskennlinie
U2
C1>C2>C3
I
Abbildung 106: Magnetisierungskennline eines Asynchronmotors (rot) und
Kondensatorkennlinien für verschiedene Kapazitätswerte
Im unteren Spannungsbereich steigt der Magnetisierungsstrom iµ des Asynchronmotors etwa
linear mit der Spannung an. Bei höherer Spannung tritt Sättigung in dem Motor auf, die
125
Induktivitätswerte für Streuung und Hauptinduktivität nehmen ab und der
Magnetisierungsstrom steigt überproportional mit der Spannung an. Der Ständerwiderstand
R1 kann für die Magnetisierung des Asynchronmotors in erster Näherung vernachlässigt
werden.
Der Kondensatorstrom ic ist linear von der Spannung abhängig. Die Steigung der
Kondensatorgeraden hängt von dem Wert der Kapazität ab. Ergibt sich aus dem
Kondensatorstrom und dem Magnetisierungsstrom ein gemeinsamer Arbeitspunkt ungleich
dem Ursprung des Koordinatensystems, so kann sich dieser als Betriebszustand einstellen.
Im Fall des Kondensatorwertes C1 würde sich die Spannung U1 an den Motorklemmen
einstellen.
Diese Spannung kann größer sein als die Motornennspannung. In diesem Fall würden die
Dioden des Wechselrichters leitend werden und den Zwischenkreis des Umrichters auf den
Scheitelwert der Motorspannung aufladen. Die Asynchronmaschine arbeitet in diesem
Betriebspunkt als Generator. Die erforderliche Energie für den Aufladevorgang wird aus der
Rotation des Läufers entnommen. In [7] wird gezeigt, dass die zurück gespeiste Leistung
höher als die Nennleistung des Motors sein kann. Für den Filterkondensator und den
Zwischenkreiskondensator besteht die Gefahr der Zerstörung durch Überspannung.
Mit geringerer Kapazität wird die Kondensatorgerade steiler. In Abbildung 106 ist dies durch
die Kennlinie des Kondensators C2 dargestellt. Im Fall von C2 stellt sich die Spannung auf
den geringeren Wert U2 ein. Ist die Kondensatorgerade im Fall von C3 steiler als die
maximale Steigung der Magnetisierungskennlinie, so kann kein Schnittpunkt der beiden
Kennlinien gefunden werden. In diesem Fall tritt das Phänomen der Selbsterregung nicht
auf.
Neben den Werten für die Bauteile L und C hängt die Selbsterregung noch von der Frequenz
des drehenden Motors ab.
Abbildung 107: Magnetisierungskennlinien und Kondensatorgeraden bei unterschiedlichen
Frequenzen
Mit steigender Frequenz neigt sich die Kondensatorgerade für einen gegeben Kapazitätswert
nach rechts, weil die Impedanz des Kondensators mit steigender Frequenz abnimmt. Die
126
Magnetisierungskennlinie des Motors neigt sich mit steigender Frequenz nach links, weil der
Magnetisierungsstrombedarf des Motors abnimmt, da die induzierte Spannung ansteigt. Bei
der höheren Frequenz ω2 stellt sich somit eine höhere Spannung an den Motorklemmen ein
als bei der niedrigeren Frequenz ω1.
Die kritische Frequenz, ab der die Selbsterregung einsetzt, kann aus Gl. (99) abgeleitet
werden. Sie ist dann erreicht, wenn die Impedanz des Motors auch ohne Berücksichtigung
von Sättigungseffekten bereits den Wert der Kondensatorimpedanz übersteigt. Es gilt:
f krit =
1
2π
(100)
(Ls1 + Lh ) C
Die kritische Frequenz wird demnach geringer, wenn der Kondensator oder die
Motorinduktivität groß werden. Die Motorinduktivität ist eine Funktion der Motorleistung, bei
kleinen Motoren ist die Induktivität und somit der Magnetisierungsstrom kleiner. Der
Kondensator besteht aus dem Filterkondensator des Sinusfilters, so dass das Kriterium der
Selbsterregung ein Auslegungskriterium für den Filterkondensator darstellt. Für die
praktische Anwendung eines Frequenzumrichters mit Sinus-Ausgangsfilter bedeutet dies,
dass bei festgelegtem Filterkondensator sowohl die maximale Ausgangsfrequenz des
Umrichters als auch die minimal anschließbare Motorleistung zu begrenzen sind.
Selbsterregung kann immer dann auftreten, wenn der Motor nicht unter der Kontrolle des
Umrichters arbeitet. Dies ist beispielsweise dann der Fall, wenn der Umrichter mit einer
bestimmten Ausgangsfrequenz arbeitet und anschließend eine Pulssperre, ausgelöst
beispielsweise durch eine Überstromabschaltung, auftritt. In diesem Fall können die
beschriebenen Begrenzungen von Ausgangsfrequenz des Umrichters und minimaler
Motorleistung eine Selbsterregung verhindern. Allerdings kann die Selbsterregung auch
dann einsetzen, wenn der Umrichter vom Netz getrennt ist und die Motorwelle durch eine
Arbeitsmaschine angetrieben wird. Aufgrund der Remanenz der Asynchronmaschine wird
sich auch in diesem Fall eine Spannung an den Motorklemmen gemäß der Kennlinien in
Abbildung 107 einstellen. In diesem Fall ist die auftretende Frequenz vom Umrichter nicht
beeinflussbar, so dass externe Maßnahmen gegen diese Betriebszustand wie beispielsweise
die Verwendung einer mechanischen Feststellbremse bei Deaktivierung des Umrichters zu
treffen sind.
Der 18,5kW Demonstratorumrichter besitzt eine Filterkapazität von 1µF in Sternschaltung.
Als maximale Ausgangsfrequenz ist ein Wert von 200Hz spezifiziert. Bei der Verwendung
standardmäßiger Maschinenparameter ist in dieser Konstellation die minimal erlaubte
Motorleistung 4kW, bei kleineren Motoren ist eine Reduzierung der maximal zulässigen
Ausgangsfrequenz erforderlich.
Die theoretischen Überlegungen können an einem Versuchsaufbau messtechnisch
nachgewiesen werden. Um eine Zerstörung des Umrichters zu vermeiden, wurde dieser
Versuch mit einer reduzierten Netzspannung von 400V durchgeführt. Als Motor wurde ein
leerlaufender Motor mit einer Nennleistung von 1,5kW verwendet. Um die kritische Frequenz
versuchsweise abzusenken, wurde die Kapazität des Sinusfilters auf 3µF erhöht. Die
kritische Frequenz beträgt in diesem Fall 87Hz. In dem Versuch wurde der Motor auf 140Hz
beschleunigt und anschließend eine Impulssperre ausgelöst.
127
Abbildung 108: Überspannung am Umrichter durch Selbsterregung der Asynchronmaschine
nach Impulssperre
In Abbildung 108 ist die Filterkondensatorspannung (blau) und der Strom in der
Filterinduktivität (grün) dargestellt. Nach der Impulssperre wird der Filterstrom zunächst null,
die Filterspannung steigt an. Sobald die Filterspannung den Wert der
Zwischenkreisspannung erreicht, beginnt der Motor, Energie in den Zwischenkreis
zurückzuspeisen. Der Zwischenkreis wird so von ursprünglich 570V (durch das
gleichgerichtete 400V-Netz) auf über 900V aufgeladen. Nach verhältnismäßig kurzer Zeit
nimmt die Filterspannung wieder ab, weil der Motor durch elektrische und mechanische
Verluste abgebremst wird. In dem Versuch wurde keine Schwungmasse oder
Arbeitsmaschine verwendet.
Für die Dimensionierung des Filterkondensators des Sinusfilters stellt die Vermeidung der
Selbsterregung somit ein wichtiges Auslegungskriterium dar. Es schränkt den Freiheitsgrad
ein, bei gewünschter Resonanzfrequenz eine Reduzierung der Filterinduktivität durch eine
Erhöhung der Filterkapazität zu erreichen.
3.4 Asymmetrischer Filter
In Kap. 3.1 wurden die Ausgangsspannungen des Umrichters hergeleitet und in
symmetrische bzw. asymmetrische Anteile zerlegt. Die bisher betrachtete Dimensionierung
des Sinusfilters hat sich auf die symmetrischen Anteile bezogen, weil diese im Motor zu
einem Stromfluss und deren Oberschwingungen zu Motorverlusten führen.
Die asymmetrischen Anteile führen zu einer Veränderung des Potenzials des
Motorsternpunktes bzw. des Potenzials der Ausgangsphasenleitungen gegenüber dem
Erdpotenzial. Auch diese asymmetrischen Spannungsanteile können zu unerwünschten
Effekten führen und sollen deshalb in diesem Kapitel betrachtet werden.
128
3.4.1 Spannungsbelastung des Motors
In [29] wird ausführlich auf die Spannungsbelastung des Motors beim Betrieb an
Pulswechselrichtern eingegangen. Im Wesentlichen sind zwei Phänomene bei der
Spannungsbelastung dominant:
a) erhöhte Spannungsbelastung an den Motorklemmen aufgrund von Reflexion
Erzeugt der Umrichter an seinen Ausgangsklemmen eine sprungförmige Spannung, so
breitet sich diese Spannung als Welle über der Motorleitung aus und trifft an den
Motorklemmen an den angeschlossenen Motor. Dort findet eine Reflexion der
Spannungswelle statt. Bezeichnet man die Amplitude der hinlaufende Welle als U0 und die
der reflektierte Welle als U0’, so gilt für die an den Motorklemmen auftretende
Spannungsamplitude U:
U = U0 + U0 '= U0 + r U0
(101)
Der Zusammenhang zwischen der ursprünglichen und der reflektierten Welle ist über den
Reflexionsfaktor r gegeben. Dieser hängt von dem Wellenwiderstand ZW und dem
Abschlusswiderstand Za der Motorleitung ab:
r=
Z a − ZW
Z a + ZW
(102)
Die am Ende der Motorleitung als Abschlusswiderstand wirkende Impedanz des Motors ist
wesentlich größer als der Wellenwiderstand der Motorleitung. Deshalb wird die
Spannungswelle an den Motorklemmen nahezu total reflektiert, die reflektierte
Spannungswelle breitet sich über die Motorleitung zurück zum Umrichter aus und überlagert
sich der hinlaufenden Welle. An den Motorklemmen besitzen sowohl die hinlaufende als
auch die rücklaufende Welle die Amplitude des ursprünglichen Spannungssprungs, so dass
an den Motorklemmen bei einer Sprunganregung mit dem Wert der Zwischenkreisspannung
die doppelte Zwischenkreisspannung als kurzzeitige Spannungsspitze messbar ist.
Besteht der Spannungssprung nicht aus einem idealen Sprung, sondern aus einer Flanke
mit der Anstiegszeit tA, so ist die Reflexion am Leitungsende von der Laufzeit der
Spannungswelle tL und somit von der Länge der Leitung und deren
Ausbreitungsgeschwindigkeit abhängig. Ist die Anstiegszeit der Spannungsflanke kürzer als
die doppelte Laufzeit über die Motorleitung, so ist die Verdopplung der Spannung am Motor
messbar. Ist die Anstiegszeit länger, so reduziert sich die Spannungsüberhöhung. Die
Ausbreitungsgeschwindigkeit entspricht im Vakuum der Lichtgeschwindigkeit. Für
Motorkabel reduziert sie sich für hohe Frequenzanteile abhängig von der relativen
Dielektrizitätskonstante der Kabelisolierung um den Faktor
1
εr
. Bei handelsüblichen
geschirmten Motorkabeln beträgt die Ausbreitungsgeschwindigkeit etwa 150m/µs, was der
Hälfte der Lichtgeschwindigkeit entspricht, für ungeschirmte Motorleitungen ist die
Ausbreitungsgeschwindigkeit höher. Für die Reduzierung der Spannungsüberhöhung
aufgrund von Reflexion kann hieraus ein Dimensionierungskriterium für die Anstiegszeit tA
der Spannungsflanke am Ausgang des Filters abgeleitet werden.
129
b) ungleichmäßige Aufteilung der Strangspannung auf die einzelnen Windungen der
Motorwicklung
Eine zusätzliche Belastung der Motorwicklung ergibt sich dadurch, dass die an den
Motorklemmen auftretende Spannung für hohe Frequenzen eine ungleichmäßige Aufteilung
auf die einzelnen Windungen der Motorwicklung zeigt. Für diese Betrachtung wird die
Motorwicklung als Kettenschaltung einzelner Windungselemente modelliert:
C’W*xW
L’*xW
C’E*xW
n-1
n
n+1
Abbildung 109: Modell einer Motorwindung
Abbildung 109 ist die n-te Windung einer Motorwicklung modelliert. Neben dieser Windung
schließen sich gleichartige Modelle für die n-1 – te und n+1 – te Windung an. L’, C’E und C’W
entsprechen dem Induktivitätsbelag, dem Kapazitätsbelag gegen Erdpotenzial und dem
Kapazitätsbelag zwischen zwei Windungen. xW bezeichnet die Windungslänge einer
Windung. Bei einer Beaufschlagung der Motorwicklung mit einer sprungförmigen Spannung
U0 verteilt sich diese nicht gleichmäßig auf alle Windungen. Die Sprungwelle kann in einen in
die Motorwicklung eindringenden und einen reflektierten Anteil zerlegt werden. Diese
Zerlegung kann anhand der Grenzfrequenz
ωg =
xW
1
L' C 'W
(103)
erfolgen, wobei die eindringende Sprungwelle alle Frequenzanteile unterhalb ωg und die
reflektierte Sprungwelle alle Frequenzanteile oberhalb ωg enthält. Die eindringende
Sprungwelle kann nur um die Kopflänge H in die Motorwicklung eindringen. Diese
Eindringtiefe entlang des Spulendrahtes berechnet sich bei sprungförmiger Spannungswelle
zu:
H = π ⋅ xW
C 'W
C'E
(104)
und hängt somit nur von dem Verhältnis der Kapazitäten zwischen den Windungen und
Erdpotenzial ab. Dieses Verhältnis hängt stark von dem Aufbau des Motors und der
realisierten Spulengeometrie ab. Innerhalb der Kopflänge muss die gesamte
Spannungsamplitude der eindringenden Sprungwelle abgebaut werden, wodurch sich eine
erhöhte Spannungsbelastung für die ersten Windungen der Motorwicklung ergibt.
Besteht die eintreffende Spannungsflanke nicht aus einem idealen Sprung, sondern aus
einer abgeflachten Flanke, so reduziert sich die Spannungsbelastung am Wicklungsanfang
erheblich. Die nur aus hohen Frequenzanteilen bestehende reflektierte Spannungswelle
entfällt. Für die Eindringtiefe der Spannungswelle ist in diesem Fall nicht mehr die durch die
Spulengeometrie bestimmte Kopflänge, sondern die Anstiegszeit der Spannungsflanke
maßgeblich.
130
Durch Einsatz des Sinusfilters sind alle symmetrischen Ausgangsspannungen des
Umrichters sinusförmig, das zugehörige Frequenzspektrum ist in Abbildung 103 dargestellt
worden. Es enthält keine nennenswerten Amplituden im hohen Frequenzbereich, so dass
eine erhöhte Spannungsbelastung des Motors aufgrund der symmetrischen Spannungen
ausgeschlossen ist.
Ein Sinusfilter mit der Struktur nach Abbildung 76 filtert jedoch nur die symmetrischen
Ausgangsspannungen des Umrichters. Die asymmetrische Spannung könnte mit dieser
Filtertopologie immer noch sprungförmig mit hoher Spannungssteilheit sein. Durch die
Ausführungsform der Sinusfilterdrosseln als einphasige, voneinander getrennte und
magnetisch nicht gekoppelte Drosseln können diese jedoch in Verbindung mit vorhandenen
Kapazitäten gegen Erde eine asymmetrische Filterwirkung besitzen. Ein entsprechendes
Ersatzschaltbild mit den Größen im asymmetrischen System ist in Abbildung 110 dargestellt.
Wechselrichter
ICOM
UCOM
Motorkabel
Filterdrossel
Motorwicklung
LF
CLFE
CKE
CME
Abbildung 110: Ersatzschaltbild des asymmetrischen Systems
Treibende Spannung für asymmetrische Ströme sind die asymmetrischen Anteile in der
Umrichterausgangsspannung. Aus einer Analyse der Gleichtaktspannung kann ermittelt
werden, dass bei kleiner Drehzahl des Motors die Amplitude der asymmetrischen Spannung
bei der Schaltfrequenz bis zu 45% der Zwischenkreisspannung betragen kann [26]. Bis zu
den Motorklemmen durchläuft diese Spannung einen Filter, dessen Induktivität analog zum
symmetrischen Filter aus der Induktivität der Sinusfilterdrossel besteht. Als Kapazität des
asymmetrischen Filters wirkt die Summe aus:
a) der Kapazität der Filterdosselwindungen gegen Erde. Das Ersatzschaltbild in Abbildung
110 ist an dieser Stelle nicht ganz korrekt, genauer müsste ein Kettenleitermodell analog
zu Abbildung 109 verwendet werden. Für eine qualitative Abschätzung ist jedoch eine
konzentrierte Kapazität am Drosselende ausreichend.
b) der Kapazität der Motorleitung gegen Erde. Diese ist stark von der Ausführungsform des
Kabels abhängig. Mit Vorhandensein eines Kabelschirms und steigender Leitungslänge
steigt der Wert dieser Kapazität an.
c) der Kapazität der Motorwicklung gegen Erde. Diese ist, wie bereits erwähnt, von der
Bauart des Motors abhängig.
Die geringste Kapazität und somit Filterwirkung ergibt sich bei der Verwendung einer
ungeschirmten Motorleitung. Deshalb wurde die asymmetrische Motorspannung bei dieser
Anordnung mit der Spannung ohne Sinusfilter verglichen. Die Messung wurde bei 70m
ungeschirmter Leitung, leerlaufendem Motor und kleiner Ausgangsfrequenz durchgeführt,
um maximale Schaltsteilheiten und eine maximale Amplitude der asymmetrischen Spannung
zu erhalten:
131
ohne_Filter
mit_Filter
kV
1.2
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2
0
10
20
µs
Abbildung 111: Spannungssteilheit am Motor mit und ohne Sinusfilter
Der Spannungsverlauf am Motor mit Sinusfilter ist in Abbildung 111 magenta, ohne
Sinusfilter bau dargestellt. Die beiden Messkurven stammen aus unterschiedlichen
Versuchen, ihre zeitliche Zuordnung zueinander ergibt sich über den Triggerpegel des
Oszilloskops.
Ohne Sinusfilter ist die Spannungsüberhöhung aufgrund der Reflexion deutlich zu erkennen.
Bei der gemessenen Anstiegszeit der Spannungsflanke von 100ns und einer
angenommenen Ausbreitungsgeschwindigkeit von mindestens 150m/µs ergibt sich als
erforderliche Kabellänge für die Totalreflexion eine Leitungslänge von maximal 30m. In dem
Versuch wurde eine ungeschirmte Motorleitung mit 70m Länge verwendet.
Durch Verwendung des Sinusfilters wird die Spannungssteilheit der Leiter-Erde-Spannung
am Motor von 10kV/µs auf unter 300V/µs reduziert. Mit dem Sinusfilter ist neben der Steilheit
der Spannungsflanke auch die Amplitude der Überspannung reduziert. Sie beträgt weniger
als 30% der Zwischenkreisspannung und ist in diesem Fall als unkritisch einzustufen. Der
Sinusfilter wirkt somit im asymmetrischen System als Element, das die Spannungssteilheit
reduziert. Ein Filter mit diesem Verhalten wird als dU/dt-Filter bezeichnet.
In dem Ersatzschaltbild in Abbildung 110 sind mehrere Kapazitäten eingezeichnet, die für die
Filterwirkung verantwortlich sein können. Um zu klären, welche Kapazität für die
Filterwirkung dominant ist, wurden weitere Messungen durchgeführt.
In einem ersten Versuch wurde die verwendete ungeschirmte Motorleitung mit einer Länge
von 70m und einem Querschnitt von 6mm2 durch eine zweite ungeschirmte Leitung mit einer
Länge von 5m und einem Querschnitt von 16mm2 ersetzt.
132
Leitung_5m
kV
1.5
1.0
0.5
0.0
-0.5
-1.0
-20
-15
-10
-5
0
5
10
15
µs
Abbildung 112: Leiter-Erde-Spannung am Motor mit 5m Leitung
Die Steilheit der Spannungsflanke beträgt in diesem Fall etwa 400V/µs und ist damit etwa
30% größer als im Fall der 70m langen Leitung. Aufgrund der geringeren Kapazität der
kurzen Leitung wäre zu erwarten gewesen, dass diese Anstiegszeit um den Faktor 3,5
geringer ist. Im Umkehrschluss folgt daraus, dass die Kapazität der Leitung nicht die
dominante Größe für die Filterwirkung des asymmetrischen Filters darstellt.
Auffällig ist in Abbildung 112 im Besonderen, dass die maximale Spannungsamplitude bei
der kurzen Leitung mit größerem Querschnitt deutlich höher ist und mit ca. 1300V nahezu
den Maximalwert von 1500V erreicht, der bei einem völlig ungedämpften System zu erwarten
wäre. Dies bedeutet, dass die Leitungsverluste der Motorleitung einen großen Einfluss auf
die Dämpfung der asymmetrischen Spannung besitzen.
Um den Einfluss der Windungskapazität der Filterdrossel gegen Erde zu untersuchen, wurde
in einem weiteren Versuch der Sinusfilter gegenüber Erde isoliert aufgebaut. Die Messung
wurde wieder mit der ursprünglichen Motorleitung mit 70m Länge durchgeführt.
133
Motor_mit_isoliertem_Filter
Motor_mit_Filter
kV
1.2
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2
-10
-5
0
5
10
15
20
25
µs
Abbildung 113: Leiter-Erde Spannung am Motor bei isolierter (blau) und bei geerdeter
(magenta) Sinusfilterdrossel
Die Isolierung der Sinusfilterdrossel bewirkt kaum eine Veränderung der Anstiegsflanken der
Spannung. Als Referenz wurde die Spannungskurvenform mit dem nicht isolierten Sinusfilter
aus Abbildung 111 verwendet. Somit ist die Kapazität der Motorwicklung in Verbindung mit
der Filterinduktivität für die asymmetrische Filterwirkung verantwortlich. Für die Gegenprobe
wurde anschließend eine Messung mit Sinusfilterdrossel ohne angeschlossenen Motor
durchgeführt:
ohne_Filter
ohne_Motor
kV
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
0
10
20
µs
Abbildung 114: Ausgangsspannung am Sinusfilter ohne Motor (magenta) und am Motor ohne
Filter (blau)
134
Ohne Motor, aber mit Sinusfilter ist die Spannungssteilheit der Leiter-Erde-Spannung nahezu
ebenso hoch wie beim Betrieb mit Motor ohne Sinusfilter. Dies bestätigt die Vermutung, dass
die Filterwirkung nicht durch die Windungskapazität der Filterdrossel, sondern die
Wicklungskapazität des Motors erreicht wird. In dem Kurvenzug der Spannung ohne Motor in
Abbildung 114 ist das Überschwingen des asymmetrischen Filters wieder deutlich zu
erkennen, weil die dämpfende Wirkung der Motorleitung entfällt.
3.4.2 Resonanz des asymmetrischen Filters
Wie bereits erwähnt, liegt die Resonanzfrequenz des asymmetrischen Filters oberhalb der
Schaltfrequenz, wodurch dieser Filter als dU/dt-Filter und nicht als Sinusfilter wirkt. Werden
am Ausgang des Umrichters weitere Komponenten angeschlossen, so kann die
Resonanzfrequenz des asymmetrischen Filters absinken, weil die zusätzlichen
Komponenten die Gesamtkapazität der Anordnung gegen Erde erhöhen können.
Wird diese Gesamtkapazität so groß, dass die Resonanzfrequenz des asymmetrischen
Filters in den Bereich der Schaltfrequenz des Umrichters oder einer ihrer Oberschwingungen
kommt, so besteht die Gefahr, dass dieser asymmetrische Filter angeregt wird [35]. Im
Ersatzschaltbild in Abbildung 110 ist die Kapazität des Motorkabels mit aufgeführt. Diese
Kapazität steigt mit der Länge der Motorleitung an. Ein typischer Wert für den
Kapazitätsbelag eines geschirmten Motorkabels liegt bei ca. 1nF/m. Aus der Anstiegszeit in
Abbildung 113 lässt sich eine Ersatzkapazität des Motors gegen Erde von ca. 2,7nF ableiten.
Dies bedeutet, dass beim Einsatz eines geschirmten Motorkabels dieses auch bei kurzen
Längen bereits zu einer weiteren Reduzierung der Spannungssteilheit am Motor führt.
Bei einer Leitungslänge von 140m beträgt die Resonanzfrequenz des asymmetrischen
Filters ca. 16kHz und kann daher von der Pulsfrequenz des Umrichters angeregt werden.
Die Spannung an einer Motorklemme gegen Erde wurde daraufhin mit Leitungslängen von
0m und 140m simuliert. Um eine möglichst große Anregung des asymmetrischen Filters zu
erhalten, wurde die Simulation mit einer kleinen Motorfrequenz von 5Hz durchgeführt.
2000
1500
1000
ULE/[V]
500
0
-500
-1000
-1500
-2000
30
30.1
30.2
30.3
30.4
30.5
30.6
30.7
30.8
30.9
t/[ms]
Abbildung 115: Spannung an den Motorklemmen gegen Erde bei 0m (blau) und 140m
(magenta) geschirmter Motorleitung
135
31
Bei der Simulation mit 0m Motorleitung (blaue Kurve) ist die aus den Messungen in
Abbildung 112 bekannte pulsförmige Spannung mit reduzierter Steilheit zu erkennen. Die
Spannungsüberhöhung durch Reflexion ist in dem Simulationsmodell nicht berücksichtigt.
Beim Einsatz der 140m langen Motorleitung (magenta Kurve) ist eine Überhöhung dieser
Spannung um den Faktor 3 zu erkennen. Die Periodendauer der Schwingung in der
Motorspannung entspricht recht genau der Pulsfrequenz, wodurch die Anregung
hervorgerufen wird. Der aufgrund der Resonanz des asymmetrischen Filters fließende Strom
beträgt im simulierten Fall 14Aeff und ist damit in der gleichen Größenordnung wie der
Laststrom des Motors mit 19A. Neben unzulässig hoher Spannungsbelastung am Motor
verursacht die Resonanz somit auch eine thermische Überlastung der Leistungshalbleiter
und der Sinusfilterdrossel.
Die Anregung des asymmetrischen Filters beim Einsatz langer, geschirmter Motorleitungen
kann verhindert werden, indem eine zusätzliche stromkompensierte Ausgangsdrossel
eingesetzt wird. Für das asymmetrische System ergibt sich damit folgendes Ersatzschaltbild:
Wechselrichter
Filterdrossel
ICOM
UCOM
Motorkabel
Stromkompensierte
Drossel
LF
Motorwicklung
LCOM
CLFE
CKE
ULE
CME
Abbildung 116: Ersatzschaltbild des asymmetrischen Systems mit stromkompensierter
Drossel
Vernachlässigt man beim Einsatz langer, geschirmter Motorleitungen die Kapazitäten der
Filterdrossel und des Motors, so errechnet sich die Resonanzfrequenz des asymmetrischen
Systems aus der Summe der Induktivitäten von Sinusfilterdrossel und stromkompensierter
Drossel sowie der Kapazität des geschirmten Kabels. Die stromkompensierte Drossel ist so
zu dimensionieren, dass die Resonanzfrequenz des asymmetrischen Systems wieder unter
die Schaltfrequenz gedrückt wird, so dass dieses nicht angeregt wird. Im Fall des
Demonstratorumrichters kann durch den Einsatz einer Drossel mit einer Induktivität von
4,3mH die Resonanzfrequenz des asymmetrischen Systems auf 6kHz reduziert werden.
800
600
400
ULE/[V]
200
0
-200
-400
-600
-800
30
30.1
30.2
30.3
30.4
30.5
30.6
30.7
30.8
30.9
31
t/[ms]
Abbildung 117: Leiter-Erde-Spannung am Motor mit 140m geschirmter Leitung und
stromkompensierter Drossel (magenta) sowie ohne Leitung (blau)
136
Mit der stromkompensierten Drossel und damit verbunden der Resonanzfrequenz des
asymmetrischen Filters von 6kHz wird auch die Leiter-Erde-Spannung einer Sinusfilterung
unterzogen. Als Referenz ist in Abbildung 117 die Leiter-Erde-Spannung ohne
Berücksichtigung einer Ausgangsleitung (blau) aus Abbildung 115 mit darstellt. Eine
Resonanzüberhöhung ist mit der stromkompensierten Drossel und der langen
Ausgangsleitung nicht feststellbar, bei der Pulsfrequenz von 16kHz ist eine Reduzierung der
Amplitude um den Faktor 5 messbar, was aufgrund der Übertragungscharakteristik des
asymmetrischen Filters zu erwarten ist.
Der Einsatz einer stromkompensierten Drossel stellt somit eine wirksame Methode dar, bei
langer Ausgangsleitung eine Resonanz mit der Sinusfilterdrossel zu verhindern. Die
Induktivität der stromkompensierten Drossel ist auf die Kapazität des angeschlossenen
Motorkabels abzustimmen. Deshalb ist es sinnvoll, die stromkompensierte Drossel nicht fest
in den Umrichter mit zu integrieren, sondern nur im Bedarfsfall einzusetzen.
3.4.3 Lagerströme
Eine weitere kritische Auswirkung gepulster Spannungen am Motor sind Lagerströme, die
die Lager des Motors beschädigen [11]. Die gepulste Spannung ist für die Lagerströme die
treibende Kraft, Kapazitäten im Motor stellen die erforderlichen Strompfade zur Verfügung.
Neben den Kapazitäten spielt die Leitfähigkeit des Lagers, die eine drehzahlabhängige
Größe darstellt, eine wichtige Rolle.
F
F
Niedrige
Drehzahl
Hohe
Drehzahl
Abbildung 118: Wälzlager bei niedriger und bei hoher Drehzahl
Bei geringer Drehzahl (<100rpm) wird durch die Belastung des Lagers mit der Kraft F das
Lagerfett in dem Zwischenraum zwischen den Lagerringen und den unteren Wälzkörpern
verdrängt. Somit entsteht eine leitfähige Verbindung zwischen dem Innenring und dem
Außenring des Lagers. Die elektrische Kontaktfläche zwischen dem Innen- und dem
Außenring des Lagers hängt von der elastischen Verformung der Walzen ab. Die
Kontaktfläche ist i.a. sehr klein, so dass auch bei mäßigem Lagerstrom hohe Stromdichten
erreicht werden können, die zu lokalen Schädigungen des Lagers führen. Bei hoher
Drehzahl bildet dich ein durchgängiger Schmierfilm des Lagerfetts aus, der bis zu seiner
Durchschlagsspannung das Verhalten einer Kapazität zeigt.
Die Lagerströme bestehen aus unterschiedlichen Anteilen, die in Folgenden kurz erläutert
werden sollen.
137
CWS
B
CRS
CWR
RSF
CSF
VCOM
izirkular
Rotor
ZRE
Lager
Statorwicklung
Stator
ZSE
Abbildung 119. Schnittbild durch eine Asynchronmaschine
CWS: Kapazität der Statorwicklung zum Statorblechpaket
CWR: Kapazität der Statorwicklung zum Rotor
CRS: Kapazität des Rotors zum Statorblechpaket
CSF: Kapazität des Lagerschmierfilms
RSF: Widerstand des Lagerschmierfilms
ZSE: Erdungsimpedanz des Stators
ZRE: Erdungsimpedanz des Rotors
In Abbildung 119 ist das Schnittbild einer Asynchronmaschine schematisch dargestellt. Die
Statorwicklung liegt im Statorblechpaket, auf die Darstellung der Wickelköpfe wurde
verzichtet. Die elektrisch wirksamen Kapazitäten sind in rot eingezeichnet. Man
unterscheidet folgende unterschiedliche Arten von Lagerströmen:
a. Zirkularströme
Zirkularströme fließen in der „Leiterschleife“ Stator – Lager 1 - Rotor – Lager 2 –Stator und
sind in Abbildung 119 schematisch durch den blauen Strompfad dargestellt. Sie werden
durch magnetische Flussanteile hervorgerufen, die in Umdrehungsrichtung des Rotors
verlaufen, in Abbildung 119 ist dieser Magnetfluss im oberen Teil aus der Zeichenebene
heraus und im unteren Teil in die Zeichenebene hinein dargestellt. Eine Ursache für diese
Flussanteile besteht in magnetischen Unsymmetrien beim Aufbau des Motors. Diese
Ursache ist im Elektromaschinenbau seit vielen Jahrzehnten bekannt [28]. Sie tritt auch bei
Motoren auf, die direkt am Netz betrieben werden. Beim Betrieb eines Motors an einem
Pulswechselrichter kommen weitere Flussanteile in dieser Richtung durch Erdströme hinzu,
die in der Kapazität zwischen Statorwicklung und Statorblechpaket fließen. Im Gegensatz zu
den klassischen Zirkularströmen aufgrund magnetischer Unsymmetrie enthalten die von der
gepulsten Leiter-Erde-Spannung verursachten Zirkularströme hohe Frequenzanteile.
b. Kapazitive Ströme
Zur Erläuterung der kapazitiven Lagerströme wird für das in Abbildung 119 dargestellte
Schnittbild der Asynchronmaschine ein elektrisches Ersatzschaltbild abgeleitet:
138
LF
Umrichterausgang
LK
Statorwicklung
CWR
Rotor
RSF/2
iCOM
CKE
CWS
CRS
2CSF
VCOM
iEDM
RSF
Erde
Statorblech
ZSE
ZRE
Abbildung 120: Ersatzschaltbild für kapazitive Lagerströme
Für eine bessere Übersichtlichkeit sind in magenta sind die einzelnen Knoten des
Ersatzschaltbildes mit Komponenten der realen Anordnung bezeichnet. Für erste
Überlegungen wird die Erdungsimpedanz des Rotors als hochohmig und die
Erdungsimpedanz ZSE des Stators als niederohmig angenommen.
Die gepulsten asymmetrischen Spannungsanteile des Umrichters werden über die
Filterinduktivität LF und die Ersatzkomponenten des Motorkabels LK und CKE an die
Statorwicklung übertragen. Über die Kapazität der Statorwicklung fließt ein
dementsprechender kapazitiver Strom, der, wie bereits erläutert, zu Zirkularströmen über die
Lager führen kann. Zusätzlich fließt ein weiterer kapazitiver Strom über die Kapazität CWR.
Diese Kapazität beträgt typischerweise etwa 1% von CWS, der Strom ist dementsprechend
geringer. Dieser Strom teilt sich nun auf und fließt über die Parallelschaltung aus der
Kapazität CRS zwischen Rotor und Stator und der Lagerimpedanz. Die Höhe dieses
kapazitiven Lagerstromes hängt damit von dem Verhältnis der beteiligten Kapazitäten ab. In
der Praxis hat sich gezeigt, dass diese kapazitiven Lagerströme gering sind, insbesondere
wegen der geringen Kapazität der Wicklung zum Rotor, und keine kritische Größe für den
Lagerverschleiß darstellen.
c. Kapazitive Rotorerdströme
Für den Fall, dass der Rotor des Motors eine geringere Erdungsimpedanz aufweist als der
Stator (ZRE << ZSE), sind weitere kapazitive Rotorerdströme zu beobachten, die das Lager
belasten. In diesem Fall fließen die verhältnismäßig großen Ströme in CWS über die
Lagerimpedanz und ZRE zum Umrichter zurück. Zwar bietet CWR einen Alternativpfad zum
Lager für diese Ströme, diese Kapazität ist jedoch etwa um den Faktor 10 kleiner als CWS, so
dass über das Lager in diesem Fall ein deutlich höherer Strom fließen kann als bei
niederohmig geerdetem Statorblechpaket. Da der Rotor beispielsweise über eine
Arbeitsmaschine eine niederohmige Erdung aufweisen kann, ist für die Vermeidung dieser
kapazitiven Rotorerdströme über das Lager eine möglichst niederohmige Erdung des Stators
anzustreben.
d. EDM-Ströme
Für den Fall hoher Drehzahlen kann sich über dem dann durchgehenden Schmierfilm eine
Spannung aufbauen. Übersteigt diese den Wert der Durchbruchspannung des Schmierfilms,
so wird dieser niederohmig, und es kann kurzzeitig ein hoher Strom fließen. In Abbildung 120
wechselt die nichtlineare Impedanz von einem hochohmigen auf einen niederohmigen Wert
vergleichbar einer Zündfunkenstrecke. Nach einem Verlöschen dieses EDM-Stroms (Electric
Discharge Machining) wird die nichtlineare Impedanz wieder hochohmig, und die Aufladung
kann erneut beginnen.
139
Da der Entladekanal in diesem Fall sehr niederohmig ist, kann der kurzzeitige EDM-Strom
erhebliche Werte annehmen. Als treibender Energiespeicher für die EDM-Ströme stehen die
Kapazität des Schmierfilms CSF und die Kapazität zwischen Rotor und Statorblechpaket CRS
zur Verfügung. Messbar sind nur die EDM-Ströme, die von CRS getrieben werden, da eine
Strommessung direkt im Lagerschmierfilm nicht möglich ist. Da die Kapazität des
Schmierfilms jedoch klein gegen die Kapazität CRS ist [11], werden damit die wesentlichen
EDM-Ströme erfasst.
Aus der Literatur ([11], [48], [78]) ist eine Vielzahl von Maßnahmen bekannt, um die
Lagerstromproblematik zu verbessern:
¾ Isolierung eines Lagers oder beider Lager: Diese Lösung ist mit zusätzlichen Kosten
verbunden, weil Lager mit einer isolierenden Schicht am Außenring teuerer sind als
Standardlager. Zudem werden die Lagerströme nur reduziert, da die Lagerisolation
für hohe Frequenzen wie eine Kapazität wirkt und somit hochfrequente Ströme nicht
unterbindet. Lager mit keramischen Kugeln können die Lagerströme unterbinden,
sind jedoch noch teurer.
¾ Niederohmige Erdung des Stators: Diese Maßnahme verhindert in erster Linie
kapazitive Rotorerdströme. Hierbei ist auf eine gute Anbindung des Kabelschirms der
Motorleitung und eine Erdung des Stators über niederinduktive Litzen zu achten.
Diese Maßnahmen sind analog zu den Maßnahmen für einen EMV-gerechten Aufbau
des Antriebsstrangs. Insbesondere bei bestehenden Anlagen kann diese Maßnahme
einen erheblichen finanziellen Aufwand mit sich führen.
¾ Erdung des Rotors zum Stator: Mit einer Wellenerdungsbürste kann der Rotor mit
dem Stator verbunden werden. Diese Verbindung liegt parallel zu den Lagern und
reduziert somit deren Strombelastung. Nachteilig wirkt sich aus, dass Bürsten einen
erhöhten Wartungsaufwand bedingen und Einbauraum benötigen.
¾ Betrieb des Antriebsstranges an einem IT-Netz: Netze mit isoliertem Sternpunkt
bringen in den Strompfad des asymmetrischen Ersatzschaltbildes eine zusätzliche
Kapazität ein, weil die asymmetrische Spannungsquelle aus Abbildung 120 nicht
mehr direkt mit dem Bezugspotenzial verbunden ist. Lagerströme werden dadurch
reduziert. Allerdings sind in der realen Anwendung nicht immer isolierte Netze
vorhanden, so dass mit einem zusätzlichen Transformator der Antriebsstrang vom
Netz getrennt werden müsste.
Alle diese genannten Maßnahmen resultieren in einem zusätzlichen Aufwand und reduzieren
lediglich die Symptome der Lagerströme, aber nicht deren Ursache. Der Ursache kann
reduziert werden, indem die Spannungsflanken der asymmetrischen Spannung abgeflacht
werden. Deshalb ist zu erwarten, dass die in Kap. 3.4.1 erläuterte Reduzierung der Steilheit
der asymmetrischen Spannungsflanken auch bzgl. Lagerströmen eine Entlastung bewirkt.
Deshalb wurden die Lagerströme eines Asynchronmotors bei Betrieb an dem
Demonstratorumrichter mit und ohne Sinusfilter gemessen. Für die Messung wurden an
einer präparierten Maschine beide Lageraußenringe gegen das Statorblechpaket durch
Einlegen einer Kunststofffolie isoliert und anschließend die Isolationsschichten jeweils mit
einer elektrischen Leitung überbrückt. In einer Überbrückungsleitung kann so der Lagerstrom
gemessen werden. Weil die höchste Spannungssteilheit und –amplitude der Leiter-ErdeSpannung mit kurzer Motorleitung mit großem Querschnitt gemessen wurde, wurde die
Lagerstrommessung unter Verwendung dieser Motorleitung durchgeführt. Die Motordrehzahl
betrug bei der Messung 1200rpm, so dass der Lagerschmierfilm als isolierende Schicht
sicher ausgebildet ist.
140
Lagerstrom_ohne_Sinusfilter
Lagerstrom_mit_Sinusfilter
A
A
10
1.0
8
0.8
6
0.6
4
0.4
2
0.2
0
0.0
-2
-0.2
-4
-0.4
-6
-0.6
-8
-0.8
-10
-1.0
4.3
4.4
4.5
4.6
ms
Abbildung 121: Messung des Lagerstroms ohne Sinusfilter (blau, linke Skala) und mit
Sinusfilter (magenta, rechte Skala)
Durch den Einsatz des Sinusfilters wird die Amplitude der Lagerströme etwa um den Faktor
10 reduziert. Die grundsätzliche Form beider Lagerstromkurven ist sehr ähnlich.
In Abbildung 121 ist die Summe aller Lagerstromanteile gemessen worden. Rotorerdströme
sind ausgeschlossen, da der Motor ohne Arbeitsmaschine betrieben wurde und der Rotor
deshalb isoliert ist. Zudem wurde der Stator niederohmig auf einem Maschinenbett
angebracht. Um zu klären, welcher Typ von Lagerströmen dominant ist, wurde der
Versuchsaufbau modifiziert.
In einem ersten Test wurde an einem Lager die Überbrückung der Lagerisolation entfernt.
Damit können Zirkularströme nur noch bedingt fließen, weil nun ihr Strompfad theoretisch
unterbrochen ist. Tatsächlich wirkt die Isolation als Kapazität, die hochfrequente Lagerströme
noch immer fließen lässt, allerdings ist zu erwarten, dass der Zirkularstromanteil reduziert ist.
141
Lagerstrom_ohne_Sinusfilter
ein_Lager_isoliert
A
7.5
5.0
2.5
0.0
-2.5
-5.0
-7.5
5.40
5.45
5.50
5.55
5.60
5.65
5.70
ms
Abbildung 122: Lagerströme mit und ohne einseitige Lagerisolation ohne Einsatz des
Sinusfilters
Bei gepulsten Umrichterausgangsspannungen kann durch die Lagerisolation der Lagerstrom
etwa halbiert werden. Die Reduzierung ist auf die Reduzierung der Zirkularströme, bedingt
durch die erhöhte Impedanz im Zirkularstromkreis, zurückzuführen.
Lagerstrom_mit_Sinusfilter
ein_Lager_isoliert
A
1.2
1.0
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
-0.8
-1.0
-1.2
5.5
6.0
6.5
7.0
7.5
ms
Abbildung 123: Lagerströme mit und ohne einseitige Lagerisolation bei Einsatz des Sinusfilters
142
Bei Einsatz des Sinusfilters ist eine Reduzierung der verbleibenden Lagerströme nicht oder
allenfalls geringfügig zu erkennen. Daraus ist zu schließen, dass Zirkularströme beim Einsatz
des Sinusfilters entweder keine bedeutende Rolle spielen oder lediglich ein Grundrauschen
auf niedrigem Niveau messbar ist.
EDM-Ströme können vermieden werden, indem die Motorwelle an dem Lager, an dem der
Lagerstrom gemessen wird, mit dem Lageraußenring niederohmig verbunden wird. Dadurch
wird die Kapazität des Lagerschmierfilms überbrückt, so dass sich über diesem keine
Spannung aufbauen kann, die sich in EDM-Strömen entlädt.
Die Messungen der Lagerströme bei geerdeter Motorwelle zeigen sowohl mit als auch ohne
Sinusfilter keine Veränderung zu Abbildung 122 bzw. Abbildung 123. EDM-Ströme spielen
somit eine untergeordnete Rolle. Dies bedeutet im Umkehrschluss, dass die verbleibenden
Lagerströme bei einseitig isoliertem Lager aus Abbildung 122 (magenta Kurve) ebenfalls
zum überwiegenden Teil aus Zirkularströmen bestehen, die durch die Kapazität der
Lagerisolation fließen.
Aus den Messungen der Lagerströme am Demonstratorumrichter kann somit festgehalten
werden, dass den wesentlichen Anteil der Lagerströme beim Betrieb ohne Sinusfilter
Zirkularströme bilden. Durch Lagerisolation können diese reduziert werden, allerdings nur
um etwa 40%. Mit Sinusfilter und dessen asymmetrischer Wirkung können die Lagerströme
auf 10% des ursprünglichen Wertes reduziert werden. Das messbare Lagerstromniveau ist in
diesem Fall so gering, dass als Ursache des verbleibenden Lagerstromes kein
Lagerstromtyp eindeutig zugewiesen werden kann.
3.5 EMV-Verhalten
3.5.1 Grundlagen und Messaufbau
EMV (Elektro-Magnetische Verträglichkeit) ist definiert als der Zustand eines Gerätes oder
einer Anlage, in einer definierten Umgebung zufriedenstellend zu funktionieren und
seinerseits diese Umgebung nicht unzulässig zu stören. Um dies zu erreichen, sind in
Normen (z.B. IEC61800-3, DIN EN 55011) Grenzwerte für maximal zulässige
Störaussendungen und minimal erforderliche Störfestigkeit definiert. In diesem Kapitel sollen
die Störaussendungen des Umrichterleistungsteils betrachtet werden.
In IEC61800-3 sind für die Klassifizierung von Umrichtern mehrere Klassen und
Umgebungsbedingungen definiert. Für jede Klasse sind zulässige Grenzwerte der
Störaussendung definiert, die ein Gerät für die Erfüllung dieser Klasse einhalten muss.
Frequenzumrichter in der Leistungsklasse des Demonstrators für den Einsatz in
Industrieanlagen werden üblicherweise für die Grenzwertklasse C2 ausgelegt. Die
normativen Grenzwerte sollen an dieser Stelle jedoch nur informativ mit aufgeführt sein, der
Fokus dieses Kapitels richtet sich auf die Auswirkungen, die der Einsatz eines Sinusfilters
auf die Störaussendungen besitzt.
Störaussendungen können in Form von Störspannungen und Störströmen auf Leitungen
sowie als elektromagnetische Abstrahlung auftreten. Deshalb wird grundlegend zwischen
leitungsgebundener Funkstörspannung und Störabstrahlung unterschieden. Für beide Arten
der Störaussendung sind unterschiedliche Frequenzbereiche definiert, in denen Störpegel zu
messen und Grenzwerte einzuhalten sind.
143
Die Funkstörspannung ist im Bereich von 150kHz bis 30MHz mit Grenzwerten belegt.
Anhand eines Ersatzschaltbildes soll die Entstehung und Messung der Funkstörspannung im
Folgenden erläutert werden:
Umrichtergehäuse
L1
Netz
L2
L3
PE
Netznachbildung
Kabelschirm
LCOM
GR
CLE
M
WR
CZKE
CWRE
CKS + CMG
CKE + CME
Abbildung 124: Ersatzschaltbild der Messanordnung für leitungsgebundene EMVStöraussendung
Die Funkstörspannung wird durch einen Messempfänger erfasst, der an der
Netznachbildung angeschlossen wird. Die Netznachbildung wird zwischen das
Versorgungsnetz und den Prüfling geschaltet. Sie besitzt die Aufgabe, für den Prüfling ein
Versorgungsnetz mit definierter Impedanz zur Verfügung zu stellen ([119], [121]). Zusätzlich
besitzt die Netznachbildung genormte Messimpedanzen, an denen ein Spannungsabfall, die
Funkstörspannung, messbar ist. Die in der Netznachbildung gemessene Funkstörspannung
ist ein Maß für die Störspannung, der andere Verbraucher in einem realen Netz ausgesetzt
wären.
Als Störquelle für leitungsgebundene Störungen tritt primär der Wechselrichter in
Erscheinung. Andere mögliche Störquellen wie Schaltnetzteile für umrichterinterne
Stromversorgungen oder hochfrequent taktende Digitalelektronik sollen an dieser Stelle nicht
betrachtet werden, weil der Sinusfilter auf diese Störquellen keinen Einfluss besitzt.
Kritisch für die EMV-Messung sind alle die vom Wechselrichter hervorgerufenen Störströme,
die ihren Stromkreis nur über die Netznachbildung und damit über die Messimpedanzen
schließen können. Dies sind in erster Linie die Störströme, die über die rot gezeichneten
Kapazitäten CWRE, CKE, CME, CKS und CMG abfließen. Die blau eingezeichneten Komponenten
CZKE, CLE und LCOM sind Komponenten, die zur Verbesserung des EMV-Verhaltens eingefügt
werden können. In Verbindung mit dem Kabelschirm und den Gehäusen von Umrichter und
Motor dienen sie dem Versuch, den Strompfad der vom Takten des Wechselrichters
hervorgerufenen Störströme zu schließen, ohne dass die Netznachbildung im Stromkreis
liegt.
Die Kapazitäten CWRE bestehen aus den Kapazitäten der Strombahnen der hochfrequent
getakteten Wechselrichterausgangsleitungen und den ersten Windungen der
Sinusfilterdrossel gegenüber dem Umrichtergehäuse. Mit den Kapazitäten CZKE und CLE wird
versucht, deren Ströme zum Wechselrichter zurück zu führen. Ohne die EMVKondensatoren CZKE und CLE würden die in CWRE fließenden Störströme ihren Rückweg über
den PE-Anschluss des Umrichters und die Netznachbildung zum Wechselrichter nehmen
und somit zum in der Netznachbildung gemessenen Störstrom beitragen. Wichtig ist hierbei
wie bei allen EMV-Kondensatoren, dass diese ebenso wie ihre Anbindung geringe
Induktivitäten besitzen, weil sich der Störstrom gemäß der Impedanzen auf die EMVKondensatoren und den Weg über die Netznachbildung aufteilt und im betrachteten hohen
Frequenzbereich auch geringe Induktivitäten zu nennenswerten Impedanzen führen.
Deshalb wird in den Weg über die Netznachbildung noch mit LCOM eine stromkompensierte
Drossel eingefügt [93], die für alle asymmetrischen Ströme eine zusätzliche hohe Impedanz
darstellt und den Weg der Störströme über die Netznachbildung erschwert.
Die Kapazitäten CWRE
bestehen
z. B. aus der Kapazität der Kupferbahnen in
Halbleitermodul gegen die Modulbodenplatte. Da diese beiden Potenziale nur durch eine aus
144
thermischen Gründen möglichst dünne Keramik voneinander getrennt sind und sich flächig
gegenüberstehen, bildet sich aus den geometrischen Abmessungen und dielektrischen
Eigenschaften der Keramik eine Kapazität. Für zusätzliche Kapazitätsanteile durch die
Ausgangsleitungen des Wechselrichters gegenüber Erde ist zu erwarten, dass sie aufgrund
des integrierten Sinusfilters und damit verbunden der kurzen Leitungslänge gering sind.
Allerdings besitzt auch die Sinusfilterdrossel eine Kapazität ihrer Windung gegen den Kern,
der an dieser Stelle für die ersten Windungen der Drossel als zusätzliche Kapazität wirkt,
weil der Kern der Sinusfilterdrossel niederohmig geerdet ist. In Summe ergeben sich somit
gegenläufige Tendenzen bzgl. Erhöhung oder Reduzierung der Kapazitäten in Vergleich zu
einem Umrichter ohne integrierten Sinusfilter, die sich gegenseitig in erster Näherung
kompensieren.
Die Kapazitäten CKS bzw. CMG bestehen aus den Kapazitäten der Motorleitungen und den
Motorwicklungen gegen Kabelschirm bzw. Motorgehäuse. Insbesondere bei langen
Motorleitungen können diese Kapazitäten hohe Werte annehmen. Für die dort fließenden
beträchtlichen Ströme ist eine möglichst niederinduktive Anbindung des Kabelschirms an das
Umrichtergehäuse und das Motorgehäuse sehr wichtig, damit auch diese Störströme über
den Kabelschirm, das Gehäuse sowie CZKE und CLE zum Wechselrichter zurück geführt
werden können. Bei Einsatz eines Sinusfilters ist aufgrund der dann geringen
Spannungssteilheiten der Potenziale der Motorleitungen gegenüber der Bezugserde zu
erwarten, dass die Amplitude dieser Störströme durch den Sinusfilter reduziert wird.
Die Kapazitäten CKE und CME bestehen aus verbleibenden Kapazitäten der Motorleitungen
und der Motorwicklungen gegenüber der Bezugserde. Diese sind i.a. deutlich geringer als
die Kapazitäten CKS und CME, sind jedoch in ihrer Wirkung wesentlich kritischer, weil deren
Ströme nicht über den Kabelschirm an den Wechselrichter zurückgeführt werden können
und somit der einzige Pfad für diese Ströme in dem Weg über die Netznachbildung liegt. Bei
der Verwendung von Motorleitungen ohne Kabelschirm sind diese Kapazitäten größer als bei
der Verwendung eines Kabelschirms, weil die schirmende Wirkung entfällt. Durch die
reduzierten Spannungssteilheiten ist auch bei den Strömen in CKE und CME zu erwarten,
dass sie durch den Sinusfilter reduziert werden.
3.5.2 Leitungsgebundene Störaussendung
Um den Einfluss des Sinusfilters auf die Funkstörspannung zu bewerten, wurden
vergleichende Messungen an einem Antrieb mit langen, ungeschirmten Motorleitungen
durchgeführt. In diesem Versuchsaufbau kann die Wirkung des Sinusfilters am besten
festgestellt werden, da verhältnismäßig hohe Störpegel zu erwarten sind und nicht die
Gefahr besteht, dass die Wirkung des Sinusfilters durch andere Effekte, z.B. von
Schaltnetzteilen, überlagert wird.
Um den erforderlichen großen Wertebereich der Störspannungen darstellen zu können, wird
die Funkstörspannung in der logarithmischen Einheit von dBµV dargestellt [72]. Dabei gilt der
Zusammenhang:
⎛ U ( f )⎞
⎟⎟
U stör ( f )[dBµV ] = 20 lg⎜⎜ stör
⎝ 1µV ⎠
(105)
145
dBuV
100
90
80
QPClassA
Quasipeak
C2
70
AVClassA
Average C2
60
Ustör
50
40
30
20
10
0
0.15
1
10
PAGE 1
Frequenz
30
MHz
Abbildung 125: Messung der Funkstörspannung des Demonstratorumrichters mit 300m
ungeschirmter Motorleitung ohne Sinusfilter
In Abbildung 125 sind zwei Messkurven zu sehen. Die grüne Kurve wird als Average-Wert
bezeichnet und stellt den zeitlichen Mittelwert der gemessenen Funkstörspannung dar. Die
rote Kurve ist die Quasipeak-Messung. Diese Messmethode beinhaltet eine
Scheitelwertmessung der Funkstörspannung, wobei im Gegensatz zu einer reinen
Scheitelwertmessung der Speicherkondensator eine definierte Entladezeitkonstante besitzt,
wodurch neben dem absoluten Scheitelwert auch die Wiederholfrequenz der
Funkstörpannungsamplituden in den Messwert mit eingeht. Diese beiden Messmethoden
haben sich in der EMV-Technik als Standard durchgesetzt. Beide sind mit Grenzwerten
versehen, die für ein Gerät in einer definierten Umgebung einzuhalten sind. In Abbildung 125
sind in magenta Farbe die beiden Grenzwertkurven für Average und Quasipeak
informationshalber mit eingezeichnet, wobei die untere Kurve die Grenzwerte für den
Average und die obere Kurve die Grenzwerte für den Quasipeak darstellen. Beide
Grenzwerte werden deutlich überschritten.
Neben den beiden Messkurven sind in Abbildung 125 wie auch in allen folgenden
Messkurven noch blaue Kreuze zu sehen. Diese stellen Messwerte mit erhöhter Genauigkeit
im Vergleich zu den durchgehenden Kurven dar und werden bei allen Frequenzen
durchgeführt, bei denen lokale Maxima der in den durchgehenden Kurven auftreten. Im
Gegensatz zu den durchgehenden Kurven stellen diese Kreuze die mit hoher Genauigkeit
ermittelten Störpegel und somit das relevante Kriterium z.B. zu Bestehen einer EMV-Prüfung
dar.
146
dBuV
100
90
80
QPClassA
Quasipeak
C2
70
AVClassA
Average C2
60
Ustör
50
40
30
20
10
0
0.15
1
10
PAGE 1
Frequenz
30
MHz
Abbildung 126: Messung der Funkstörspannung des Demonstratorumrichters mit 300m
ungeschirmter Motorleitung mit Sinusfilter
Aus dem Vergleich von Abbildung 126 mit Abbildung 125 ist zu erkennen, dass durch den
Sinusfilter die EMV-Grenzwerte abgesenkt werden können. Insbesondere im Bereich bis
1MHz wird eine Verbesserung von über 20dBµV erreicht. Der maximale Störpegel im
gesamten Frequenzbereich wird um ca. 10dBµV reduziert. Verantwortlich hierfür ist allein die
Induktivität des Sinusfilters, weil ein zusätzlicher Versuch mit entfernten symmetrischen
Filterkondensatoren keine Veränderung der EMV-Messwerte im Vergleich zu Abbildung 126
ergibt. Dieses Ergebnis ist analog zu dem Ergebnis aus Kapitel 3.4.3, in dem die
Lagerströme betrachtet wurden, und ist auf die reduzierte Spannungssteilheit der
Motorleitungen gegenüber Erde und damit verbunden der geringeren asymmetrischen
Störströme zu erklären.
Der Sinusfilter leistet somit einen Beitrag zur Verbesserung des EMV-Verhaltens, ist jedoch
allein nicht in der Lage, die Einhaltung der Grenzwerte für die Klasse C2 beim Betrieb mit
ungeschirmten Motorleitungen zu bewerkstelligen. Hierfür ist noch ein zusätzlicher common
mode Filter am Umrichterausgang erforderlich.
Mit einem common mode Ausgangsfilter, das eine stromkompensierte Drossel mit einer
Induktivität von 30µH und Kondensatoren von 10nF gegen Erde enthält, können auch mit
ungeschirmter Motorleitung die Grenzwerte der Klasse C2 in der Funkstörspannung
eingehalten werden:
147
Quasipeak C2
Ustör
Average C2
Frequenz
Abbildung 127: Funkstörspannung bei ungeschirmter Motorleitung mit Sinusfilter und
zusätzlichem common mode Filter
In einem Wärmelauf des Umrichters mit dem zusätzlichen common mode Ausgangsfilter war
keine messbare Temperaturerhöhung der Leistungshalbleiter im Umrichter feststellbar, was
den Schluss zulässt, dass die zusätzliche Strombelastung für die Halbleiter durch den
Ausgangsfilter gering ist. An den Sinusfilterdrosseln war eine Temperaturerhöhung von 4,2K
feststellbar, was einer zusätzlichen Erhöhung um ca. 8% (vgl. Kap. 3.3.2.2) entspricht.
Diese Temperaturerhöhung ist auf hochfrequente Ströme zurückzuführen, die durch die
Kondensatoren des common mode Ausgangsfilters und somit auch durch die
Sinusfilterdrosseln fließen. Diese hochfrequenten Ströme führen in den Sinusfilterdrosseln
zu zusätzlichen Kernverlusten.
Beim Einsatz geschirmter Motorleitungen ist der zusätzliche common mode Filter für die
Einhaltung der Grenzwerte nicht erforderlich. Deshalb ist es für eine Anwendung vorteilhaft,
diesen nicht in den Umrichter zu integrieren, sondern nur bei Bedarf einzusetzen. Sollte der
zusätzliche common mode Filter mit geschirmten Motorleitungen eingesetzt werden, ist auf
die Resonanzfrequenz des asymmetrischen Filters zu achten (vgl. Kap. 3.4.2), weil die
Induktivität der zusätzlichen common mode Drossel für die Resonanzfrequenz des
asymmetrischen Filters mit zu berücksichtigen ist.
148
3.5.3 Strahlungsgebundene Störaussendung
Bei der strahlungsgebundenen Störaussendung sind zur Beurteilung des Einflusses des
Sinusfilters Messungen mit geschirmter Motorleitung zweckmäßig, da bei ungeschirmter
Motorleitung die Pegel der Störaussendung so hoch sind, dass die Messtechnik gefährdet
wird. Bei dieser Messung wird in einem genormten Abstand von 10m die
Störspannungsfeldstärke im Bereich von 30MHz bis 1000MHz mit einer Antenne erfasst
[114]. Die Messung wird in einem Raum durchgeführt, in dem die Reflexion der Wände
minimiert ist, damit möglichst nur die direkte Störstrahlung erfasst wird. Analog zur
Funkstörspannung wird auch die Störfeldstärke im logarithmischen Maßstab angegeben:
⎛
⎞
⎜ E ( f )⎟
⎡ µV ⎤
⎜ stör
⎟
E stör ( f )⎢dB
⎥⎦ = 20 lg⎜ µV ⎟
m
⎣
⎜ 1
⎟
m ⎠
⎝
(106)
Estör
Class C2
Frequenz
Abbildung 128: Strahlungsgebundene Störaussendung des Demonstrators bei Betrieb ohne
Sinusfilter
Ohne Sinusfilter wird der zulässige Grenzwert der Feldstärke deutlich überschritten und liegt mit
52dBµV/m bei 38MHz um mehr als 10dBµV/m über dem zulässigen Grenzwert. In Abbildung 128 ist
zu beachten, dass nur die eingezeichneten Kreuze verlässliche Messwerte darstellen, während die
angezeigte Kurve lediglich informativen Charakter besitzt und die Aufgabe hat, kritische Frequenzen
für die verlässliche Messung zu selektieren.
Mit Sinusfilter sind die Pegel der Störstrahlung deutlich reduziert, teilweise bis zu 30dBµV/m.
Ursache hierfür ist ebenfalls der Einfluss der Sinusfilterdrossel, weil eine Änderung der
symmetrischen Kondensatoren keine Veränderung der Messkurve ergibt.
149
dBµV/m
Estör
Class C2
Frequenz /[MHz]
MHz
Abbildung 129: Strahlungsgebundene Störaussendung des Demonstrators bei Betrieb mit
Sinusfilter
Mit dem Einsatz des common mode Filters wird die Messung der Störstrahlung auch mit
einer ungeschirmten Motorleitung möglich:
Estör
Class C2
Frequenz
Abbildung 130: Strahlungsgebundene Störaussendung des Demonstrators mit zusätzlichem
common mode Filter und ungeschirmter Motorleitung
150
Durch den common mode Filter kann die strahlungsgebundene Störaussendung so stark
abgesenkt werden, dass die maximal messbaren Pegel im Bereich der zulässigen
Grenzwerte liegen.
Zusammenfassend kann aus den EMV-Messungen die Schlussfolgerung gezogen werden,
dass der Sinusfilter eine Reduzierung der Störaussendung des Umrichters sowohl
leitungsgebunden als auch in der Feldstärkemessung bewirkt. Die Ursache liegt in der
asymmetrischen Wirkung des Sinusfilters. Durch den gezielten Einsatz eines common mode
Filters mit stromkompensierter Drossel kann jedoch eine noch größere Wirkung erzielt
werden. Aus diesem Grund sollte der EMV-Gesichtspunkt für die Auslegung des
symmetrischen Sinusfilters bzw. dessen Drossel nicht im Vordergrund stehen.
151
4 Zusammenfassung
In der vorliegenden Arbeit wurde ein Umrichterleistungsteil für eine Anschlussspannung von
690V und einer Nennleistung von 18,5kW mit Sinusausgangsfilter konzipiert, welches im
Vergleich zu heutigen Umrichtern mit einer erhöhten Schaltfrequenz arbeitet und somit eine
Aufwandsreduzierung für den Sinusfilter zur Folge hat.
Im ersten Teil der Arbeit wurden hierfür verschiedene Lösungsmöglichkeiten für die
Halbleiterrealisierung diskutiert und miteinander verglichen. Wird als aktiver Schalter ein
IGBT verwendet, so ist dieser auf Kosten des Durchlassverhaltens für geringe Schaltverluste
zu optimieren. Für die Freilaufdiode gilt dies ebenfalls, wobei ein besonders großer Vorteil
durch den Einsatz von Schottkydioden als Freilaufdiode erzielt werden kann.
Schottkydioden für die erforderliche Sperrspannung von 1700V können heute nur mit dem
Halbleitermaterial Siliziumkarbid (SiC) realisiert werden. Die grundlegenden physikalischen
Eigenschaften dieser Bauelemente wurden erläutert. Da aus Gründen der Ausbeute diese
Schottkydioden zur Zeit nur als kleine Chips mit verhältnismäßig geringer Stromtragfähigkeit
von 7A wirtschaftlich hergestellt werden können, wurde die Parallelschaltung der Chips und
das damit eingehende derating betrachtet.
Für die verschiedenen Lösungsmöglichkeiten wurden anschließend vergleichende
Dimensionierungen durchgeführt. Hierbei zeigt sich, dass für geringe Schaltfrequenzen bis
4kHz die SiC-Diode nur verhältnismäßig geringe Vorteile bietet, die kaum in der Lage sind,
den höheren Flächenpreis für das Halbleitermaterial SiC zu rechtfertigen. Bei hohen
Schaltfrequenzen wie 16kHz sind die Vorteile jedoch beachtlich. Neben der erforderlichen
Halbleiterfläche werden auch die anfallenden Verluste des Umrichters durch den Einsatz der
SiC-Dioden deutlich reduziert. Bei noch höherer Schaltfrequenz von 64kHz ist mit SiFreilaufdioden mitunter überhaupt keine wirtschaftliche Lösung möglich, weil die Verluste
exorbitant werden.
Für Lösungen in der Zukunft sind auch unipolare Hochvoltschalter aus SiC denkbar. Diese
Bauelemente sind heute noch stark in der Entwicklungsphase. Deshalb wurde eine
theoretische Abschätzung geliefert, welche Dimensionierung bei idealisiertem
Schaltverhalten denkbar ist. Dabei stellt sich heraus, dass eine sehr hohe Schaltfrequenz
wirtschaftlich realisierbar ist, aber auch eine entsprechende Erhöhung der
Schaltgeschwindigkeit erfordert, die ihrerseits erhöhte Anforderungen an z.B. die dU/dtFestigkeit potenzialtrennender Komponenten stellt. Bei heute verwendeten bipolaren IGBTs
sind die Vorteile durch eine starke Erhöhung der Schaltgeschwindigkeit begrenzt, weil die
inhärente Speicherladung der IGBTs dadurch nicht beeinflusst werden kann.
Im zweiten Teil der Arbeit wurde die vorteilhafte Gestaltung des Sinusfilters diskutiert.
Grundlage hierfür sind die zu filternden Komponenten der Ausgangsspannung, wobei
besonders das symmetrische System für die Dimensionierung der Sinusfilterdrossel wichtig
ist. Die Abhängigkeit des Drosselvolumens von der Umrichterschaltfrequenz und dem zu
wählenden Ripplestrom des Filters wurden theoretisch und anhand realer Lösungsvarianten
aufgezeigt. Dabei zeigt sich, dass für die realen Lösungsmöglichkeiten neben dem
theoretischen Optimum auch die Verfügbarkeit von Kernbauformen für unterschiedliche
Schaltfrequenzen und Leistungen eine Rolle spielt.
Die Rückwirkung der Dimensionierung des Ripplestroms auf den Halbleiterbedarf im
Motorwechselrichter
wurde
anhand
von
Simulationen
mit
dem
Schaltkreissimulationsprogamm Simplorer diskutiert. Es zeigt sich, dass diese Rückwirkung
nicht unerheblich ist, weil ein steigender Ripplestrom erhöhte Halbleiterverluste mit sich
152
bringt, so dass der Ripplestrom nicht beliebig groß gewählt werden darf. Anschließend wurde
ein allgemeines Auslegungsoptimum hergeleitet, welches eine Dimensionierung der
Filterdrossel und der Halbleiter in Abhängigkeit des Kostenverhältnisses beider
Komponenten erlaubt. Für den motorseitigen Wechselrichter des Demonstratorumrichters
wurden eine Schaltfrequenz von 16kHz und eine Filterinduktivität von 0,7mH als Ergebnis
der Optimierungen gewählt. Als Halbleiterbauelemente wurden in dem motorseitigen
Wechselrichter planare IGBTs und SiC-Schottky-Freilaufdioden verwendet.
Die Dimensionierung des Filterkondensators ist bzgl. des Kostenaufwandes untergeordnet,
weil der Kondensator wesentlich kostengünstiger als die Drossel ist. Allerdings wird der
Kondensatorwert durch die auftretende Selbsterregung begrenzt, die abhängig von der
zulässigen Drehzahl des Antriebes z.B. bei Pulsperre des Wechselrichters auftreten und zur
Zerstörung des Umrichters durch Überspannung führen kann.
Der realisierte, symmetrisch wirkende Sinusfilter zeigt in Verbindung mit Kapazitäten der
Motorleitungen und der Motorwicklungen gegen Erde auch eine asymmetrische Filterwirkung
als dU/dt-Filter. Die verbleibende Spannungssteilheit von unter 500V/µs ist gegenüber einer
Lösung ohne Sinusfilter so weit reduziert, dass die Isolationsbeanpruchung des Motors,
insbesondere der Windungsisolation der ersten Motorwindungen, deutlich reduziert wird. Aus
dem gleichen Grund ist auch die Belastung des Motors bezüglich Lagerströmen stark
reduziert.
Die Reduzierung der asymmetrischen Ströme durch die reduzierte Spannungssteilheit der
Motorleitungen gegenüber Erdpotenzial führt darüber hinaus zu einer Verbesserung
Störaussendungen des Umrichters.
Als abschließendes Urteil kann festgehalten werden, dass die Verwendung einer erhöhten
Schaltfrequenz des Motorwechselrichters in einem Umrichterleistungsteil mit Sinusfilter
deutliche Vorteile bzgl. des Bauvolumens mit sich bringt. Für eine optimierte Lösung sind als
Freilaufdioden
Schottkydioden aus SiC erforderlich, um die Schaltverluste des
Wechselrichters zu beherrschen. Bei zukünftiger Verfügbarkeit von unipolaren
Hochvoltschaltern aus SiC kann die Schaltfrequenz dabei noch weiter erhöht werden. Über
einen möglichen Kostenvorteil auf Materialkostenbasis entscheidet das Verhältnis von Filterzu Halbleiterkosten.
153
5 Abstract
In this theses, the power stage of a frequency converter for 690V mains voltage and 18.5kW
has been designed. The converter power stage operates at high switching freqency,
reducing therefore the effort for an integrated sine wave output filter.
In the first part of the theses, different variants of power semiconductors are compared. If an
IGBT is used as active switch, it has to be optimized for high switching frequency. For the
freewheeling diode, a huge benefit can be generated by using schottky diodes.
Today, schottky diodes for a breakdown voltage of 1700V can only be realized in SiC. The
basic physical character of this semiconductor material is described. As only small chips with
a current capability of 7A are available today, the paralleling of several chips is discussed in
detail.
For a small switching frequency like 4kHz, savings in losses due to SiC are relatively small.
For 16kHz, the improvement is remarkeable. For 64kHz, even the Si IGBT could be replaced
by a unipolar SiC switch. In this case, it is favourable to increase the switching speed of the
unipolar SiC switch.
In the second part of the theses, the favourable design of the sine wave filter is discussed.
The dependancy of the volume of the filter choke of the switching frequency is discussed
theoretically and by practical variants.
The effect of the rating of the ripple current on the semiconductor losses is simulated. This
effect is remarkeable and has to be taken into account. For the demonstrator of 18.5kW, a
switching frequency of 16kHz and a filter inductance of 0.7mH was found to be the best
compromise.
The rating of the filter capacitor and the maximum motor speed are limited by avoiding the
self excitation of the the motor.
The filter inductance in conjunction with capacitances to ground limits the dV/dt of the output
voltage to ground to less than 500V/µs. This reduces the stress of the motor insulation.
Furthermore, bearing currents are reduced significantly as well EMI disturbance.
As a final remark, it can be stated that by increasing the switching frequency, the volume of a
sine wave filter can be reduced significantly. For an optimized solution, SiC freewheeling
diodes are required to reduce the switching losses of the inverter. The economical
acceptance of that solution depends on the cost ratio of filter - and semiconductor costs.
154
6 Abkürzungen und Formelzeichen
^
2QS
Scheitelwert einer Größe
Zwei-Quadrantensteller
A
A
α
A**
Aaktiv,Chip
Aaktiv,Wafer
Anode
Fläche, allgemein
Winkel, allgemein
effektive Richardson-Konstante
Aktive Fläche eines Halbleiterchips
Summe aller aktiven Chipflächen auf einem Wafer
B
b
βn
magnetische Flussdichte
Breite
Exponentialterm der Temperaturabhängigkeit von SiC
C
C
γ
C’E
CF
CKE
CKS
CLFE
CLE
CME
CMG
CRS
CSF
CU
C’W
CWR
CWRE
CWS
Czk
CZKE
Collectoranschluss eines IGBT
Kondensator, allgemein
Stromwinkel
Kapazitätsbelag gegen Erde
Filterkondensator
Kapazität der Motorleitung gegen Erde
Kapazität der Motorleitung gegen den Kabelschirm
Kapazität der Wicklung der Filterdrossel gegen Erde
Kapazität zwischen einem Leiter und Erde
Kapazität der Motorwicklung gegen Erde
Kapazität der Motorwicklung gegen das Motorgehäuse
Kapazität des Rotors zum Statorblechpaket
Kapazität des Lagerschmierfilms
Leitermaterial, z.B. Kupfer
Kapazitätsbelag einer Windung gegen eine Nachbarwindung
Kapazität der Statorwicklung zum Rotor
Kapazität der getakteten Wechselrichterausgangsleitungen gegen Erde
Kapazität der Statorwicklung zum Statorblechpaket
Zwischenkreiskondensator
Kapazität zwischen einem Zwischenkreisanschluss und Erde
D
D
D
δ
∆
DCB
DCN
DCP
di/dt
du/dt
DUT
ds
Drainanschluss
Diode, allgemein
Defektdichte
relative Einschaltdauer in einer Modulationsperiode
Differenz, allgemein
Keramiksubstrat (Direct Copper Bonding)
negativer Anschluss des Zwischenkreises
positiver Anschluss des Zwischenkreises
Stromsteilheit, allgemein
Spannungssteilheit, allgemein
Device Under Test
inkrementale Weglänge
E
E
Emitteranschluss eines IGBT
elektrische Feldstärke
155
E
ε
ε0
εr
Eadd1,Eadd2
EC
EdT1
Edyn
Ekrit
EF
EFH
EFM
Eg
Eoffd
EonIGBT
Es
Estör
EV
Energie, allgemein
Dielektrizitätskonstante eines Materials
Dielektrizitätskonstante des Vakuums
relative Dielektrizitätskonstante eines Materials
zusätzliche Verlustenergie
unterstes Energieniveau des Leitungsbandes
Durchlassverlustenergie im Transistor T1
Verlustenergieanteil durch dynamische Sättigungsspannung
kritische elektrische Feldstärke eine Halbleitermaterials
Ferminiveau, allgemein
Ferminiveau des Halbleiters
Ferminiveau des Metalls
Bandabstand zwischen Valenzband und Leitungsband
Ausschaltverlustenergie einer Diode
Einschaltverlustenergie eines IGBT
Schaltverlustenergie
Störfeldstärke
oberstes Energieniveau des Valenzbandes
f
F
φ,Φ
Φ
Φ
Φb
ΦH
ΦM
F3E
f(E)
FE
fout
fs
Frequenz, allgemein
Kraft
Phasenwinkel zwischen Strom und Spannung
magnetischer Fluss
Potenzial, allgemein
Potenzial der Schottkybarriere
Austrittsarbeit des Halbleiters
Austrittsarbeit des Metalls
Fundamental Frequency Front End, aktive Gleichrichterschaltung in B6Schaltung mit grundfrequent getakteten Halbleiterschaltern
Fermiverteilung
magnetisches Kernmaterial, z.B. Eisen
Ausgangsfrequenz des Umrichters
Schaltfrequenz
G
G
Gd
GdM
GR
Gateanschluss eines aktiven Halbleiterschalters
Übertragungsfunktion, allgemein
Übertragungsfunktion unter Berücksichtigung der Dämpfung
Übertragungsfunktion unter Berücksichtigung der Dämpfung und des Motors
Gleichrichter
H
H
magnetische Erregung
Kopflänge
I
IA
IC
ICN
ICOM
ID
ID
IDN
Im
Iµ
ILast
ILW1
ILWh
Strom, allgemein
Ausgangsstrom eines Schaltungsteils
Collectorstrom eines IGBT
Collectornennstrom eines IGBT
common mode Strom
Strom in einer Diode
Drainstrom eines JFET
Nennstrom einer Diode
Imaginärteil
Magnetisierungsstrom eines Motors
Laststrom
grundfrequenter Anteil des Stromes in der Filterinduktivität in Phase W
hochfrequenter Anteil des Stromes in der Filterinduktivität in Phase W
156
Imittel
Imittel
IS
Strommittelwert
Strommittelwert
Ständerstrom eines Motors
J
JFET
Stromdichte
Junction Field Effect Transistor
k
K
K0, K1, K2
KD
Kges
KH
Boltzmann-Konstante
Kathode
Koeffizienten, allgemein
Kosten für die Filterdrossel
Gesamtkosten für Filterdrossel und Halbleiter
Kosten für die Halbleiter
L
L’
l
LCOM
LCU
LF
Lh
LK
LM
LRB
Ls
Ls1
L’s2
LSB
Induktivität, allgemein
Induktivitätsbelag
Weglänge, allgemein
Induktivität einer stromkompensierten Drossel
Induktivität einer Kupferbahn auf der DCB
Filterinduktivität
Hauptinduktivität des Motors
Induktivität der Motorleitung
Streuinduktivität des Motors
Induktivität eines Rahmenbonddrahtes
Streuinduktivität
Streuinduktivität der Statorwicklung
auf die Statorseite umgerechnete Streuinduktivität des Rotors
Induktivität eines Substratbonddrahtes
M
M
M
max
µ
µ0
µn
µp
µr
Modulationsindex
Motor
Kreismittelpunkt
Maximalwert
Permeabilität, allgemein
Permeabilität des Vakuums
Beweglichkeit der Elektronen
Beweglichkeit der Löcher
relative Permeabilität eines Materials
n
n
N
n+
nNA
NC
ND
ni
nr
NV
negative geladene freie Ladungsträger, Elektronen
Anzahl, allgemein
Dotierungskonzentration, allgemein
hohe Elektronenkonzentration
geringe Elektronenkonzentration
Dotierungskonzentration der Akzeptoren
Anzahl der möglichen Energiezustände im Leitungsband
Dotierungskonzentration der Donatoren
intrinsische Ladungsträgerkonzentration
n-Dotierungskonzentration auf der rechten Seite des pn-Übergangs
Anzahl der möglichen Energiezustände im Valenzband
p
p+
Ψ
PD
Pd
positiv geladene freie Ladungsträger, Löcher
hohe Löcherkonzentration
magnetischer Gesamtfluss
Verluste einer Diode
Durchlassverluste
157
PdD2
PdDU0
PdDV0
PdDW0
PdT1
PdTU0
PdTV0
PdTW0
PDU
PDV
PDW
PJFET
Ps
PSBD
PsU0
PsV0
PsW0
PT
PTU
PTV
PTW
pl
Durchlassverluste in der Diode D2
Durchlassverluste in der Diode der Phase U bei Ausgangsfrequenz 0Hz
Durchlassverluste in der Diode der Phase V bei Ausgangsfrequenz 0Hz
Durchlassverluste in der Diode der Phase W bei Ausgangsfrequenz 0Hz
Durchlassverluste im Transistor T1
Durchlassverluste im Transistor der Phase U bei Ausgangsfrequenz 0Hz
Durchlassverluste im Transistor der Phase V bei Ausgangsfrequenz 0Hz
Durchlassverluste im Transistor der Phase W bei Ausgangsfrequenz 0Hz
Verluste in der Diode in Phase U
Verluste in der Diode in Phase V
Verluste in der Diode in Phase W
Verluste des JFET
Schaltverluste
Verluste der Schottkydiode
Schaltverluste der Bauteile in der Phase U
Schaltverluste der Bauteile in der Phase V
Schaltverluste der Bauteile in der Phase W
Verluste eines Transistors bzw. IGBTs
Verluste in des IGBT in Phase U
Verluste in des IGBT in Phase V
Verluste in des IGBT in Phase W
p-Dotierungskonzentration auf der linken Seite des pn-Übergangs
q
Q
Elementarladung
Speicherladung eines Leistungshalbleiters
r
R
ρ
R’2
Re
Ron
rpm
RSF
Rsub
Rth
RthjhT
Reflexionsfaktor
Widerstand, allgemein
eingeschlossene Ladung
auf die Statorseite umgerechneter Läuferwiderstand
Realteil
ohmscher Ersatzwiderstand einer linearisierten Durchlasskennlinie
Umdrehungen pro Minute
Widerstand des Lagerschmierfilms
Substratwiderstand
Thermischer Widerstand, allgemein
thermischer Widerstand zwischen der Sperrschicht eines IGBT und der
Oberseite des Kühlkörpers
thermischer Widerstand zwischen der Sperrschicht einer Diode und der
Oberseite des Kühlkörpers
thermischer
Widerstand
zwischen
dem
Kühlkörper
und
der
Umgebungstemperatur
RthjhD
Rthha
s
Si
SiC
Schlupf
Silizium
Siliziumkarbid
t
T
T
T
Θ
Zeit, allgemein
Transistor, allgemein
Temperatur, allgemein
Dauer einer Grundschwingungsperiode
Durchflutung
Zeitkonstante, allgemein
Temperatur der Umgebung
Temperatur der Modulbodenplatte
Anstiegszeit
τ
Ta
Tc
tA
158
tf
tL
Th
TjT
TjD
tp
Fallzeit
Laufzeit
Temperatur des Kühlkörpers
Sperrschichttemperatur eines IGBT
Sperrschichttemperatur einer Diode
Modulationsperiode
U
U, V, W
U0
U0’
UA
UCE
UCE0
UCE1
UCEN
UCEsat
UCOM
UCU,UCV, UCW
UD
UD0
UDN
UdT1
UDrift
UDS
Uh
UiM
ULE
ULM
ULW
US
Usmax
UstA
Ustör
Uth
UW
UWD
UWD1
UWDh
Uzk
Spannung, allgemein
Wechselspannungsanschlüsse des Wechselrichters
hinlaufende Spannungswelle
rücklaufende Spannungswelle
Ausgangsspannung
Collector-Emitter-Spannung
Schleusenspannung eines IGBT
Collector-Emitter-Spannung zum Zeitpunkt t1
Collector-Emitter-Spannung eines IGBT bei Nennstrom
Collector-Emitter-Spannung im gesättigten Zustand des IGBT
common mode Spannung
Spannungen an den Filterkondensatoren der Phasen U, V bzw. W
Spannung an einer Diode
Schleusenspannung einer Diode
Spannung an einer Diode bei Nennstrom
Durchlassspannung am Transistor T1
Driftspannung
Drain-Source-Spannung eines JFET
hochfrequente Anteile einer Spannung
innere Spannung des Motors
Leiter-Erde-Spannung
Spannungsabfall an der Streuinduktivität des Motors
Spannungsabfall an der Filterinduktivität in Phase W
Ständerspannung eines Motors
maximale Sperrspannung eines Bauelementes
Ansteuerspannung einer Treiberstufe
Funkstörspannung
Schwellenspannung
treibende Spannung für Wirbelströme
differential mode Spannung der Phase W
grundfrequenter Anteil der differential mode Spannung der Phase W
hochfrequenter Anteil der differential mode Spannung der Phase W
Zwischenkreisspannung
w
ω
ωg
Wmag
WR
ωres
Weite der schwach dotierten Mittelschicht eines Leistungshalbleiters
Kreisfrequenz, allgemein
Grenzfrequenz
magnetische Energiedichte
Wechselrichter
Resonanzfrequenz
x
xw
Weg, allgemein
Weglänge zwischen zwei benachbarten Windungen
Za
ZRE
ZSE
Zth
ZW
Abschlussimpedanz einer Leitung
Erdungsimpedanz des Rotors
Erdungsimpedanz des Stators
thermische Impedanz, allgemein
Wellenwiderstand einer Leitung
159
7 Literaturverzeichnis
[1] Agilent Technologies, Datenblatt HCNW-3120
[2] Al Jabri, A.K.; Alolah, A.I.: Capacitance requirement for isolated self-excited induction
generator, IEE proceedings 1990, Vol. 137, No. 3, p. 154 – 159
[3] Andresen, E: Skritpum zur Vorlesung Theorie elektrischer Maschinen I, Technische
Universität Darmstadt, 1992
[4] anonym, Verlustarme Magnetkerne. Weniger Spaltverlustprobleme mit
Magnetpulverkernen, Technica, Rupperswil, 2001, Bd. 50, Nr. 1/2, p. 25 - 27
[5] Baliga, B.J.; denBaars, S.; Palmour, J.; Shur, M; Spencer, M.: High voltage silicon carbide
devices, Wide bandgap semiconductors for high power, high frequency and high temperature
symposium, San Francicso, CA, USA, 1998, p. 77 - 88
[6] Bartoli, M; Reatti, A.; Kazimierczuk, M.K.: Modelling iron-powder inductors at high
frequencies, IAS 1994, Conference record of the 1994 Industry Applications Conference
Twenty-Ninth IAS annual meeting, Denver, Co, USA, vol. 2, p.1225 – 1232
[7] Bauer, F.: Rückspeiseleistung bei Impulssperre bei ASM-Antrieben mit Sinusfiltern,
Technischer Aktenvermerk Siemens AG, Erlangen 2005
[8] Bauer, H.; Langer, G.: Modelle und Strategien für Prüfungen der elektromagnetischen
Verträglichkeit (EMV), Elektrie, Berlin 1988, p. 409 – 415
[9] Bhatnagar, M.; Nakanishi, H.; McLarty, P.K.; Baliga, B.J.; Patnaik, P.; Parikh, N.:
Comparison of Ti and Pt silicon carbide schottky rectifiers, IEEE int. electron devices
meeting, San Francisco, CA, USA, 1992, p. 789 - 792
[10] Binder, A.; Rummich, E.: Besonderheiten bei der Selbsterregung von
Asynchrongeneratoren im Inselbetrieb, etz-Archiv 1990, Bd. 12, Nr. 8, p. 251 - 257
[11] Binder, A; Schrepfer,A.: Lagerströme bei umrichtergespeisten Drehstrommotoren,
Antriebstechnik 1999, Bd. 38, Nr. 8, p. 46 – 48
[12] Bodson, J.M.; De Hoe, J.M. ; Neyens, J. : Energy savings with variable-speed drives,
13th International Conference on Electricity Distribution 1995, Liège, Belgium, 1995, vol. 5, p.
16/1-6
[13] Bozorth, R.: Ferromagnetism, Van Nostrand Inc., Princeton, NJ, USA, 4. Auflage 1956
[14] Bronstein, I.N.; Semendjajew, K.A.: Taschenbuch der Mathematik, Harri Deutsch Verlag,
Frankfurt/Main, 24. Auflage 1989
[15] Bruckmann, M.: Reihenschaltung von Insulated-Gate-Bipolar-Transistoren (IGBT),
Dissertation, Friedrich-Alexander-Universität Erlangen, Erlangen 2004
[16] Bruckmann, M.; Baudelot, E.; Mitlehner, H.; Weis, B.: Switching behaviour of diodes
based on new semiconductor materials and silicon – a comparative study, EPE’97, 7th
Conference on Power Electronics and Applications, Conference Record vol. 1, p. 513 – 517,
Brussels, Belgium, 1997
160
[17] Casanellas, F.: Losses in PWM inverters using IGBTs, IEE Proceedings Electric power
applications 1994, vol. 141, No 5, p. 235 - 239
[18] Chinthavali, M.S.; Ozpineci, B.; Tolbert, L.M.: Temperature.dependant characterization
of SiC power electronic devices, IEEE Power Electronics in Transportation, Piscataway, NJ,
USA, 2004, p. 43 - 47
[19] Clausert, H.; Wiesemann, G.: Grundgebiete der Elektrotechnik, Bd. 1 + 2, 4. Auflage,
Oldenbourg Verlag, München 1990
[20] Clemente, S.M.; Dapkus, D.A. : IGBT models account for switching and conduction
losses, Power Conversion and Intelligent Motion 1993, vol. 19, no. 8, p. 51 – 54
[21] Clemente, S.M.; Pelly, B.R.: Das Schaltverhalten von Leistungs-MOSFETs, Teil 1,
Design und Elektronik 1989, Nr. 9, S. 130, 132 – 133, 136 – 138, 140 – 142, 144 – 145
[22] Clemente, S.M.; Pelly, B.R.: Das Schaltverhalten von Leistungs-MOSFETs, Teil 2,
Design und Elektronik 1989, Nr. 10, S. 91 – 92, 94
[23] Dahlquist, F.; Lendenmann, H.; Östling, M.: A JBS diode with controlled forward
temperature coeffient and high surge current capability, Materials science forum, Tsukuba,
Japan, 2001, p. 1129 – 1132
[24] Deboy, G.; Hulsken, H.; Mitlehner, H.; Rupp, R.: A comparison of modern power device
concepts for high voltage applications: field stop IGBT, compensation devices and SiC
devices, proceedings of the 2000 Bipolar/BiCMOS Circuits and Technology Meeting,
Piscataway, NJ, USA 2000, p. 134 - 141
[25] Del Vecchio, P.; Veca, G.M.: Eddy currents and field computation in superconducting
electromagnetic pump, IEEE transactions on magnetics 1983, Bd. 19, Nr. 6, p. 2389 - 2392
[26] Denzner, M.: Umrichtersystem für sinusförmige Ein- und Ausgangsgrößen mit hohen
Pulsfrequenzen und optimierten Filtern, Dissertation, Friedrich-Alexander-Universität
Erlangen, Erlangen 2003
[27] Droste, H.; Lutz, H.M.: Vergleich zweier Antriebsvarianten im Rahmen der
Modernisierung einer Seilaufzugsanlage, Lift report 1994, Bd. 20, Nr. 1, p. 30 - 34
[28] Erdman, J.; Kerkman, R.J.; Schlegel, D.; Skibinski, G.: Effect of PWM inverters on AC
motor bearing currents and shaft voltages, APEC 1995, 10th Applied Power Electronics
Conference, Proc., Vol. 1, Dallas, USA, 1995, p. 24 - 33
[29] Essig, R.: Reduzierung der Spannungsbeanspruchung von Motorwicklungen bei
Speisung über Pulswechselrichter, Dissertation, Friedrich-Alexander-Universität Erlangen,
Erlangen 1994
[30] EvoxRifa, Datenblatt PHZ3027
[31] Felsl, H.P.; Wachutka, G., Rupp, R.: The electrothermal behaviour of 4H-SiC schottky
diodes at forward bias considering single pulse and pulsed current operation, Materials
Science Forum, vol. 433 – 436, p. 839 - 842
[32] Ferch, M.: Softmagnetic materials in todays power electronic designs, PCIM Europe
2000, Nr. 7, S. 50 - 51
161
[33] Fladerer, T.: Der Asynchrongenerator im Kleinkraftwerk (Teil 1), Elektrische Maschinen
2004, Bd. 83, Nr. 5, p. 14 - 19
[34] Franke, T.: Hochfrequentes Schalten mit Leistungshalbleitern aus Silizium, Dissertation,
Technische Universität Dresden, Dresden, 1997
[35] Freydman, R.: Einfluss eines langen Kabels auf die Leiter – Erde – Spannung am Motor,
Technischer Aktenvermerk Siemens AG, Erlangen, 2004
[36] Freydman, R.: Sinusfilter für Umrichter mit hohen Grundfrequenzen, Technischer
Aktenvermerk Siemens AG, Erlangen, 2005
[37] Friedrichs, P.; Mitlehner, H.; Dohnke, K.O.; Peters, D.; Schörner, R.; Weinert, U.;
Baudelot, E.; Stephani, D.: SiC power devices with very low on resistance for fast switching
applications, 12th International Symposium on Power Semiconductor Devices and ICs, IEEE
Proceedings, Piscataway, NJ, USA, 2000, p. 213 – 216
[38] Friedrichs, P.; Mitlehner,H.; Kaltschmidt, R.; Weinert, U.; Bartsch, W.; Hecht, C.; H.;
Dohnke, K.O.; Weis, B.; Stephani, D.: Static and dynamic characteristics of 4H-SiC JFETs
designed for different blocking capabilities, Materials Science Forum, Trans Tech
Publications 2000, vol. 338 – 342, pt. 2, p. 1243 - 1246
[39] Friedrichs, P.; Mitlehner, H., Schörner, R.; H.; Dohnke, K.O.; Elpelt, R.; Stephani, D.:
Stacked high voltage switch based on SiC VJFETs, 15th International Symposium on Power
Semiconductor Devices and ICs, IEEE Proceedings, Piscataway, NJ, USA, 2003, p. 139 –
142
[40] Friedrichs, P.; Mitlehner, H.; Schörner, R.; H.; Dohnke, K.O.; Elpelt, R.; Stephani, D.:
The vertical silicon carbide JFET – a fast and low loss solid state power switching device, 9th
European Conference on Power Electronics and Applications, EPE 2001, Graz, Austria, p. 6
pp
[41] Friedrichs, P.; Rupp,R.; Silicon carbide power devices – current developments and
potential, 11th European Conference on Power Electronics and Applications, IEEE
Proceedings, Piscataway, NJ, USA 2005, p. 11 pp
[42] Garuda, V.R.; Kazimierczuk, M.K.; Ramalingam, M.L.; Tolkkinen, L.; Roth, M.D.; . Al.:
High temperature testing of a buck converter using silicon and silicon carbide diodes, 37th
Intersociety energy conversion engeneering conference, Honolulu, HI, USA, 1997, Vol. 1, p.
317 - 322
[43] Göpfrich, K.; Rebbereh, C.; Sack, L.: Fundamental frequency front end converter (F3E)
– a dc link drive converter without electrolythic capacitor, PCIM Europe, Nürnberg 2003, 20.
– 22.5.2003, Intelligent Motion p. 59 – 64
[44] Grove, A.S.: Physics and Technology of Semiconductor Devices, John Wiley & Sons,
New York, USA, 1967
[45] Haidinger, K; Rummich, E.: Beitrag zum stationären Betriebsverhaltens des
kondensatorerregten Asynchrongenerators, Elektrotechnik und maschinenbau 1984, Bd.
101, Nr. 10, p. 464 - 467
[46] Hanigovszki, N.; Poulsen, J.; Spinazzi, G.; Blaabjerg, F..: An EMC evaluation of the use
of unshielded motor cables in AC adjustable speed drives applications, 35th IEEE Power
Electronics Specialists Conference, Aachen, Germany, 2004, p. 75 - 81
162
[47] Hausberg, V.: Elektrische Lagerbeanspruchung umrichtergespeister
Induktionsmaschinen, VDI-Fortschrittsbericht, VDI-Verlag GmbH, Düsseldorf, 2002
[48] Hausberg, V; Seinsch, H.O.: Wellenspannungen und zirkulierende Lagerströme bei
Umrichter, Electrical Engeneering, Bd. 82, Nr. 6, p. 313 – 326
[49] Hentschel, E.; Niedermeier, K.; Schäfer, K.; Beanspruchung der Wicklungsisolierung in
Drehstrommaschinen, ETZ 1993, Bd. 114, Nr. 17, p. 1074 – 1077
[50] Herrmann, B.: Sinusfilter für Umrichter mit hohen Pulsfrequenzen, Technischer
Aktenvermerk Siemens AG, Erlangen 2004
[51] Hess, J.: Kriterien zur Auswahl von Ferrit-E-Kernbauformen für Schaltnetzteile, Siemens
Components 1990, Bd. 28, Nr. 1, S. 9 – 12
[52] Hess, J.: Neue Ferritmaterialien für Breitbandübertrager, MegaLink 1994, Bd. 1, Nr. 13,
S. 34 - 37
[53] Hornberger, J.; Lostetter, A.B.; Olejnickak, K.J.; McNutt, T.; Magan Lal, S., Mantooth, A.:
Silicon carbide (SiC) semiconductor power electronics for extreme high-temperature
environments, 2004 IEEE Aerospace conference proceedings, Vol. 4, p. 2438 – 2455
[54] infineon AG, Datenblatt FS50R17KE3
[55] infineon AG, Datenblatt FS75R17KE3
[56] infineon AG, Datenblatt FS100R17KS4F
[57] infineon AG, Deutsche Patentanmeldung No. 10 2006 034 599.1: Verfahren zum
Gruppieren und Verschalten aus einem Wafer gefertigter Halbleiterchips, München 2006
[58] International Rectifier, Datenblatt IRF2135, El Segundo, CA, USA, 2005
[59] Janke, W.; Oleksy, M.; Krasniewski, J.: Thermal characteristics of silicon carbide
schottky diodes, 6th International conference on microtechnology and thermal problems in
electronics, Lodz, Poland, 2005, p. 60 - 66
[60] Joshi, R.P.; Ferry, D.K.: Calculations in the temperature and field dependant electronic
mobility in β-SiC, Solid state electronics 1995, Bd. 38, Nr. 11, p. 1911 – 1916
[61] Kamigahara, S.; Matsuura, H.; Hatakeyama, T.; Watanabe, T.;Kushibe, M.; Shinoe, T.:
Parameters required to simulate electric characteristics of SiC devices for n-type 4H-SiC,
Journal of applied physics 2004, vol. 96, no. 10, p. 5601 - 5606
[62] Kolar, J.W.; Zach, F.C.; Casanellas, F.: Losses in PWM inverters using IGBTs, IEE
Proceedings Electric power applications 1995, vol. 142, No 4, p. 285 – 288
[63] Kolar, J.W.; Zach, F.C.: Losses in PWM inverters using IGBTs: on the effect of bus
clamping on the distortion of the AC side currents, IEE Proceedings Electric power
applications 1997, vol. 144, No 2, p. 169 – 171
[64] Krümmer, R.; Reimann, T.; Berger, G.; Petzoldt, J.; Lorenz, L.: On-line calculation of the
chip temperature of power modules in voltage source converters using the microcontroller,
8th European Conference on Power Electronics and Applications, EPE’99, EPE Assoc.,
Brusselles, Belgium, 1999, p. 7 - 13
163
[65] Laska, T.; Miller, G.; Pfaffenlehner, M.; Türkes, P.; Berger, D.; Gutsmann, B.; Kanschat,
P.; Münzer, M.: Short circuit properties of Trench/Field Stop IGBT – Design aspects for a
superior robustness, ISPSD’03, Proceedings of 2003 IEEE 15th International Symposium on
Power Semiconductor Devices and ICs, Piscataway, NJ, USA, 2003, p. 152 - 155
[66] Laska, T.; Münzer, M.; Pfirsch, F.; Schaeffer, C.; Schmidt, T.: The Field Stop IGBT (FSIGBT) – A new power device concept with a great improvement potential, 12th International
Symposium on Power Semiconductor Devices and ICs, Piscataway, NJ, USA, 2000, p. 355 358
[67] Locci, N.; Muscas, C.: Hysteresis and eddy currents compensation in current
transformers, IEEE transactions on power delivery, Bd. 16, Nr. 2, p. 154 – 159
[68] Lorenz, L.; Mitlehner, H.: Key power semiconductor concepts for the next decade,
Conference record of the 2002 IEEE Industry Applications Conference, 37th IAS annual
meeting, Piscataway, NJ, USA 2002, vol. 1.1, p. 564 - 569
[69] Löwenstein, U.: EMV-Prüftechnik für leitungsgebundene Störmesstechnik, elektronik
industrie, 10/1995, p. 58 – 59
[70] Malik, N.H.; Al-Bahrani, A.H.: Influence of the terminal capacitor on the performance
characteristics of a self excited induction generator, IEE proceedings, Vol. 137, No. 2, 1990,
p. 168 – 173
[71] Mc Nutt, T.; Hefner, A.; Mantooth, A., Berning, D.; Singh, R.: Compact models for silicon
carbide power devices, International semiconductor device research symposium,
Piscataway, NJ, USA, 2003, p. 272 - 277
[72] Mecke, R.; Rummel, T.: Analyse der leitungsgebundenen Funkstörspannungen am
Modell eines Pulswechselrichterantriebes, Elektrie, Bd.50, Berlin, 1996, p. 387 – 392
[73] Missous, M.; Rhoderick, E.H.; Woolf, D.A.; Wilkes, S.P.: On the Richardson constant of
intimate metal-GaAs schottky barriers, Science and Technology 1992, Bd. 7, Nr. 2, p. 218 –
221
[74] Mitlehner, H.; Bartsch, W.; Bruckmann, M.; Dohnke, K.O.; Weinert, U.: The potential of
fast high voltage SiC diodes, IEEE International Symposium on Power Semiconductor
Devices and ICs, IEEE Proceedings, New York, NJ, USA, 1997, p. 165 – 168
[75] Mitlehner, H.; Bartsch, W.; Dohnke, K.O.; Friedrichs, P.; Kaltschmidt, R.; Weinert, U.;
Weis, B.; Stephani, D.: Dynamic characteristics of high voltage 4H-SiC vertical JFETs, 11th
International Symposium on Power Semiconductor Devices and ICs, IEEE Proceedings,
Piscataway, NJ, USA, 1999, p. 339 – 342
[76] Mitlehner, H.; Friedrichs, P.; Elpelt, R.; H.; Dohnke, K.O.; Schörner, R.; Stephani, D.:
BIFET – a novel bipolar SiC switch for high voltage power electronics, Materials Science
Forum Bd. 457/460, 2004, p. 1245 - 1248
[77] Mitlehner, H.; Friedrichs, P.; Peters, D.; Schörner, R.; Weinert, U.; Weis, B.; Stephani,
D.: Switching behaviour of fast high voltage SiC pn-diodes, 10th International Symposium on
Power Semiconductor Devices and ICs, Kyoto, Japan 1998, Inst. Electr. Eng. Japan, Tokyo,
Japan, 1998, p. 127 - 130
[78] Muetze, A.; Binder; A.: Practical rules for assessment of inverter-induced bearing
currents in inverter-fed AC motors up to 500kW, IEEE Transactions on Industrial Electronics
2007, vol. 54, no. 3, p. 1614 - 1622
164
[79] Muljadi, E., Lipo, T.A., Novotny, D.W.: Power factor enhancement of induction machines
by means of solid state excitation, International conference on evolution and modern aspects
of induction machines, Proc., Torino 1986, p. 424 - 430
[80] Mutschler, P.: Skript zur Vorlesung Leistungselektronik 1 + 2, Technische Universität
Darmstadt, 1999
[81] Neudeck, P.G.: Progress toward high temperature, high power SiC devices, 21st
International symposium on compound semiconductors, San Diego, CA, USA, Bd. 141, p. 1
–6
[82] O’Neill, A.G; Vassilevski, K.V.; Nikitina, I.P.; Wright, N.G.; Horsfall, A.B.; Johnson, C.M.:
Device processing and characterisation of high temperature silicon carbide schottky diodes,
Microelectronic Engeneering 2006, vol. 83, no. 1, p. 150 - 154
[83] O’Neill, M.: The benefits of using a Cree Inc. IGBT/SiC Schottky CoPack in AC inverter
applications, Cree Inc., Durham, NC, USA, 2006
[84] Nowak, W.-D.; Schlangenotto, H.; Füllmann, M.: Verbesserung des Schaltverhaltens bei
schnellen Dioden, 4th International Macroelectronics Conference, München, 9.-10November 1988, p. 37 - 48
[85] Orellana, A.: Ansteuerung für schnell schaltende Leistungshalbleiter, Bericht, FriedrichAlexander-Universität Erlangen, Erlangen 2003
[86] Pelly, B; Clemente, S.: Choosing the optimum semiconductor for electric vehicle drives
(I), Power Conversion and Intelligent Motion 1993, vol. 19, no. 2, p. 8, 11 – 12, 14 - 16
[87] Pelly, B; Clemente, S.: Choosing the optimum semiconductor for electric vehicle drives
(II), Power Conversion and Intelligent Motion 1993, vol. 19, no. 3, p. 12 - 16
[88] Peppel, M., Weis, B.: Optimized reverse diode operation of power MOSFETs,
Conference Record of the 35th IAS Annual Meeting and World Conference on Industrial
Application of Electrical Energy, Piscataway, NJ, USA, 2000, vol.5, p. 2961 - 2965
[89] Perez, R.; Mestres, N.; Tournier, D.; Jorda, X.; Vellehi, M.; Godignon, P.: Temperature
dependence of 4H-SiC JBS and schottky diodes after high temperature treatment of contact
metal, Materials science forums, Bologna, Italy, 2005, vol. 483 – 485, p. 945 - 948
[90] Persson, E.: Transient effects in application of PWM inverters to induction motors, IEEE
Transactions on Industry Applications 1992, Vol. 28, No. 5, p. 1095 – 1101
[91] Peters, D.; Friedrichs, P.; Mitlehner, H.; Schörner, R.; Weinert, U.; Weis, B.; Stephani,
D.: Characterization of fast 4.5 kV SiC p-n diodes, 12th International Symposium on Power
Semiconductor Devices and ICs, IEEE Proceedings, Piscataway, NJ, USA, 2000, p. 241 244
[92] Peters, D.; Friedrichs, P.; Schörner, R.; Mitlehner, H.; Weis, B.; Stephani, D.: Electrical
performance of triple implanted vertical silicon carbide MOSFETs with low on resistance, 11th
International Symposium on Power Semiconductor Devices and ICs, IEEE Proceedings,
Piscataway, NJ, USA, 1999, p. 103 - 106
[93] Petzold, J.; Klinger, R., Poess, R.J.: Nanocrystalline Materials for Common Mode
Chokes, PCIM Europe 1999, Nr. 11, S. 8, 10, 12
165
[94] Pfeifer, T.; Wengerter, R.: Amorphe Metalle in induktiven Bauelementen, ETZ, Bd. 109,
No. 20, Berlin 1988, p. 958 - 961
[95] Piepenbreier, B.; Sack, L.: Regenerative drive converter with line-frequency switched
rectifier and without dc link components, 35th IEEE Power Electronics Specialists
Conference, Aachen, Germany, 2004, Vol. 5, p. 3917 – 3923
[96] Porst, A.: Bipolare Halbleiter; Hüthig und Pflaum Verlag München, Heidelberg; 2.
Auflage 1979
[97] Profumo, F.; Tenconi, A; Griva, G; Facelli, S.: How to evaluate IGBT losses on inductive
load from data sheet parameters, EPE journal 1996, vol.6, no. 2, p. 11 – 19
[98] Ray, S.: Digital simulation of B/H excursions for power system studies, IEE proceedings
1988, vol. 135, no. 3, p. 202 – 209
[99] Ray, S.: Prediction of hysteresis losses produced by distorted flux in low-loss silicon-iron
transformer core laminations, IEE proceedings 1993, vol. 140, no. 3, p. 229 - 236
[100] Rhoderick, E.H.; Williams, R.H.: Metal-Semiconductor contacts, Clarendon Press,
Oxford, UK, 2. Auflage 1988
[101] Rüedi, H.; Köhli, P.; Schneider, T.; Bresch, W.: Dynamic Gate Controller (DGC) – a
new IGBT gate drive unit for high current/high voltage IGBT modules, PCIM 95 Europe,
Official Proceedings of the 30th International Power Conversion Conference, Nuremberg, D,
1995, p. 241 - 249
[102] Ruff, M.; Mitlehner, H.; Helbig, R.: SiC devices: physics and numerical simulation, IEEE
Transactions on electron devices, 1994, vol. 41, no. 6, p. 1040 - 1054
[103] Rupp, R.; Treu, M.; Türkes, P.; Beermann, H.; Scherg, T.; Preis, H.; Cerva, H..:
Influence of overgrown micropipes in the active area of SiC schottky diodes on the long term
reliability, Materials science forum, Bologna, Italy, 2005, vol. 483 – 485, p. 925 – 928
[104] Rupp, R.; Treu, M.; Voss, S.; Bjork, F.; Reimann, T.: “2nd generation” SiC schottky
diodes: a new benchmark in SiC device ruggedness, 18th International Symposium on Power
Semiconductor Devices and ICs, IEEE Proceedings, Piscataway, NJ, USA, 2006, p. 4 pp
[105] Rupp, R.; Zverev, I.: SiC power devices: how to be competitive towards Si-based
solutions?, materials Science Forum 2003, vol. 433 – 436, p. 805 - 812
[106] Rupp, R., Zverev, I.; ed. Saddow, S.E.; Larkin, D.J.; Laks, N.S.; Schoner, A.: System
design considerations for optimizing the benefit by unipolar SiC power devices, Silicon
Carbide 2002 – Materials, Processing and Devices, Mater. Res. Soc. Proceedings,
Warrendale, PA, USA 2003, p. 329 - 340
[107] Sanyo Semiconductors, Datasheet 2SK3747
[108] Scheuermann, U.: Vorlesungsskript Aufbau- und Verbindungstechnik in der
Leistungselektronik, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen 2006
[109] Schlangenotto, H.: Leistungshalbleiterbauelemente, Vorlesungsskript, Technische
Hochschule Darmstadt, 1994
[110] Schlangenotto, H.; Füllmann, M.; Nowak, W.-D.: Schnelle Dioden, Actuator 1988,
Internationaler Wirtschafts-Transferkongress, Bremen, D, 9. – 10- Juni 1988, S 363 - 388
166
[111] Schlangenotto, H.; Niemann, E.: Switching properties of power devices on silicon
carbide and silicon, EPE-MADEP 1991, Firenze 2. – 6. September 1991, p. 0-008 – 0-013
[112] Schnell, R.; Schlapbach, U.: Realistic benchmark of IGBT-modules with the help of a
fast and easy to use simulation-tool, PCIM Europe 2004, Nürnberg, p. 258 - 263
[113] Schörner, R.; Friedrichs, P.; Peters, D.; Mitlehner, H.; Weis, B.; Stephani, D.: Rugged
power MOSFETs in 6H-SiC with blocking capability up to 1800V, Materials Science Forum,
Trans Tech Publications 2000, vol. 338 – 342, pt. 2, p. 1295 - 1298
[114] Schwarzbeck, G: Elektromagnetische Verträglichkeit (EMV), Kontakt und Studium Bd.
41, 1992, p.208 – 242
[115] Shenai, K.; Neudeck, P.G.: Performance evaluations of silicon carbide devices in
power converters, 35th Intersociety energy conversion engeneering conference, Reston, VA,
USA, 2000, Vol. 1, p. 37 – 46
[116] Siemens AG, Katalog D11.1 “Umrichter-Einbaugeräte Sinamics G110/Sinamics G120,
Dezentrale Frequenzumrichter Sinamics G120D“, 2007
[117] Singh, R.: Reliability and performance limitations in SiC power devices,
Microelectronics Reliability 2006, vol. 46, no. 5-6, p. 713 – 730
[118] Slomovitz, D.: Correction of power transformer no-load losses, measured under nonsinusoidal voltage waveforms, IEE Proceedings C, 1989, vol. 136, no. 1, p. 42 - 47
[119] Stecher, M.: Netznachbildungen für die Störmesstechnik, Neues von Rohde und
Schwarz, 1987, p. 15 – 19
[120] Stecher, M.: Verbesserte Reproduzierbarkeit von Funk-Störspannungsmessungen,
EMV-ESD 2006, Bd. 19, Nr. 5, p. 52 - 57
[121] Steffens, E.: Normnetz, ELRAD 1996, Heft 12, p.66 – 68
[122] Sundermann, R.: Transformatoren und Drosseln in modernen Anwendungen, etz 1997,
Bd. 118, Nr. 23/24, S. 56 - 58
[123] Suorsa, I: Analytical calculation formulas for an air-gapped inductor, ICEM 2000
Proceedings, International Conference on Electrical machines, Espoo, Finland, 2000, vol. 1,
p. 125 – 129
[124] Tchouange, G.: Untersuchungen zur Modellbildung und Anwendungen von TrenchIGBTs, Dissertation, Fortschritt-Berichte VDI, Reihe 9, Nr. 323, VDI Verlag GmbH,
Düsseldorf, 2000
[125] Totterdell, D.H.J.; Leske, J.W.; Jain, S.C.: High-injection open-circuit voltage decay in
pn-junction diodes with lightly doped bases, IEE proceedings, Vol. 133, Pt.1, No. 5, 1986, p.
181 – 184
[126] Treu, M.; Rupp, R.; Kapels, H.; Bartsch, W.: Temperature dependence of forward and
reverse characteristics of Ti, W, Ta and Ni schottky diodes on 4H-SiC, Materials Science
Forum, Trans Tech Publications 2001, vol. 353 – 356, p. 679 – 682
[127] Türkes, P.; Sigg, J.: Electro-thermal simulation of power electronic systems,
Microeletronics Journal, vol. 29, no. 11, p. 785 – 790, Paris, France, 1996
167
[128] Wang, D.: Synchronous rectifier MOSFET driver substantially reduces power adapter
heat, APEC 2005, 20th Annual IEEE Applied Power Electronics Conference and Exposition,
Piscataway, NJ, USA, 2005, vol. 2, p. 700 – 705
[129] Weis, B.; Braun, M.; Friedrichs, P.: Turn-off and short circuit behaviour of 4H-SiC
JFETs, 9th European Conference on Power Electronics and Applications, Graz 2001, EPE
Assoc., Brussels, Belgium 2001, p.8 pp
[130] Weis, B.; Peters, D.; Wölz, M.: A new 690V AC drive with integrated sine wave output
filter and SiC schottky freewheeling diodes, Proceedings SPS/IPC/DRIVES 2006, VDEVerlag, Berlin 2006, p. 159 - 168
[131] Weitzel, C.E.; Palmour, J.W; Carter, C.H.jr.; Moore, K.; Nordquist, K.J.; Allen, S.;
Thero, C.; Bhatnagar, M.: Silicon carbide high power devices, IEEE transactions on electron
devices 1996, Bd. 34, Nr. 10, p. 1732 - 1741
[132] Zenger, M.; Schostek, S.: Siferrit N67: Leistungsübertragerwerkstoff extrem verlustarm
bis über 200kHz, Siemens Components 23, Heft 4 1985, p. 140 - 142
[133] Zetterling, C.: Process technology for Silicon carbide devices, IEE INSPEC, London,
UK, 2002
[134] Zhang, X.; Goldsman, N.; Bernstein, B.J.; McGarrity, J.M.; Powell, S.K.: Numerical end
experimental characterization of 4H-SiC schottky diodes, 2003 International semiconductor
devices research symposium, Washington, DC, USA, p. 120 - 121
[135] Zwanziger, P.: EG-Richtlinien für die elektrische Antriebstechnik und
Leistungselektronik, Antriebstechnik, 1995, Bd. 34, Nr. 11, p. 55 – 56, 59 – 60, 62
168