GEOMETRISCHE OPTIK

Kapitel 14
GEOMETRISCHE OPTIK
Die geometrische Optik ist die erste
Näherung zur Wahrheit. Lichtstrahlen definiert man als dünne Bündel von Licht, die
sich in isotropen Medien geradlinig ausbreiten, normal zur Phasenfläche. Anschaulich,
aber auf Grund von Beugungse↵ekten nicht
richtig für den Rand der Lichtbündel.
! " # $ %& $ '( ) %*+
, -& + %. / 0
1 # 2 $ & %*3 4 5 &
6 & --& $ / ) %*+
2 & / 1 & %. *3 4 5 &
( ) %*+
Die G.O. ist eine gute Näherung, solange das Strahlbündel groß ist gegen .
Man ordnet dem Lichtstrahl bestimmte Welleneigenschaften zu Wellenlänge,
Phasengeschwindigkeit, Intensität, Polarisation, und verwendet die
Postulate der geometrischen Optik:
1) Lichtstrahlen verlaufen in einem homogenen Medium als Gerade.
2) Das Medium ist durch den reellen Brechungsindex n
1 charakterisiert.
Die Laufzeit für die Strecke d ist d n/c. Das Produkt d n bezeichnet man als die
optische Weglänge.
RB
3) In einem inhomogenen Medium ist die optische Weglänge A n(~r)ds. Überkreuzende
Strahlenbündel beeinflussen sich nicht (Interferenz ist Teil der Wellenoptik).
4) Das Prinzip von Fermat gilt für Strahlen die von A nach B laufen: Die
Laufzeit ist ein Minimum d.h. die Variation der optischen Weglänge ist
Z B
n(~r) ds = 0 .
(14.1)
A
5) Daraus folgt, dass an Grenzflächen die Strahlen dem Brechungsgesetz von
Snellius folgen bzw. dass Einfallswinkel und Ausfallswinkel gleich sind.
! "# $% &&' ( ) ( # (
* + , - % &(
! " # $ % &'
!
!
!
!
. / "( 0 ( &1
+ ) ( , $&2 3 4 (
133
134
KAPITEL 14. GEOMETRISCHE OPTIK
14.1
Optische Abbildung
! "
$
#
!
# %
"
d0 =
Spiegel
a+b
d
a
! "
!
ebener Spiegel
Lochkamera
!
"
!
!
! "
#
2
y = 2px
x2 + y 2 = R 2
parabolischer Spiegel
elliptischer Spiegel
sphärischer Spiegel
Paraxialstrahlen (achsennahe) im sphärischen Hohlspiegel
Für kleine Winkel ' gilt '1 + '2 = 2 '0 , wobei '0 ⇡ tan '0 = y/R
!
!
'
1
1
2
+
⇡
z1
z2
R
!
#
!
*
%
"
In dieser Näherung ist die
Brennweite des Spiegels
"
"
$
#
)
"
%
&
'
f = R/2 .
'
(
Abbildung mit konkavem sphärischen Spiegel in Paraxialnäherung
#
!
$
%& $ '( $ )
"
!
"
*
#
+
%& + '( + )
Reelle bzw. virtuelle Bilder.
Abbildungsmaßstab:
!
"
y2 /y1 =
z2 /z1
14.2. GRENZFLÄCHEN
14.2
135
Grenzflächen
Ebene Grenzflächen
Siehe Seite 128. Für Paraxialstrahlen gilt die Näherung n1 '1 ⇡ n2 '2 . Für
n2 < n1 tritt Totalreflexion auf, wenn '2 ! 90o . Der Grenzwinkel für Totalreflexion ist sin 'g = n2 /n1 .
Prisma
Blaues Licht wird stärker gebrochen als rotes, wenn normale Dispersion vorliegt
(dn/d < 0) und das Prisma ein Medium mit höherem Index ist als die Umgebung ist (z.B. konventionelles Glasprisma in Luft). Die kleinste Ablenkung
erfolgt bei symmetrischem Strahlengang ↵1 = ↵2 .
= ↵1 + ↵2
!
# "
= ↵1 + ↵2
!
min
#
"
"
"
!
$ +, +( $ ' +, +* ."
# $
= 2↵
% &'
"
! "
!
# $
!
Die Effizienz von Strahlteilern wird durch den
Brechungsindexsprung an den Grenzflächen, bzw.
über optische Beschichtung mit /4 bzw. /2
Schichten bestimmt. Die Effizient hängt von Wel! "
lenlänge und Polarisationszustand, s oder p ab.# $ % & ' ( ) )
( $
) $
#
*
! "
! "
Sphärische Grenzflächen
werden auf Grund der einfachen Herstellung oft für Spiegel, Linsen verwendet.
Für paraxiale Strahlen ist das Gesetz
von Snellius näherungsweise gleich
n1 ↵ ⇡ n2
!
"
!
# $ %!
"
&
#
&
$ %)
In dieser Näherung ist die Brennweite
*"
'
(
' "+ '
f2 = R
(
Für dünne Linsen ist der Abstand
zwischen den Grenzflächen klein gegen
die Brennweite. (im Beispiel: bikonvex
mit gleichen Krümmungsradien). Die
Abbildungsgleichung ist
1 1
1
+ = .
g
b
f
n2
n2
n1
'
+
!" # $% # &
(
!" , $% , &
! )*
136
KAPITEL 14. GEOMETRISCHE OPTIK
! "#
$ % & ' ( )
Typen
von
Linsen :
* +, & #
$ % & ' ( )
$ % & ' ( ) #
$ % & $ , '
! "#
$ % & $ , '
* +, & #
$ % & $ , '
Für dicke Linsen führt man Hauptebenen ein.
An diesen verhalten sich einfallende Strahlen
wie in der Näherung für dünne Linsen.
!
!
"
, - * . / 0 "- 1 .
"
#
#
&
#
&
$
$
"
$
$
!
%
14.3
&
%
%
#
$
Linsenfehler
Die chromatische Abberation (Ort
des Fokus ist wegen der Dispersion für unterschiedliche Farbe verschieden) kann durch Achromate verhindert werden.
Mit sphärischer Abberation bezeichnet man den Umstand, dass der
Ort des Fokus wegen der Kugeloberfläche für achsenferne Strahlen anders
liegt als für achsennahe.
!
!
!
" # $ # % &# '
#& '
" #$ %
!
$# ( )
!
%
(
%
)
* + , #& - . '
Auf Grund des Astigmatismus werden Gegenstandspunkte, die weit von der
Achse liegen, verzerrt abgebildet. Die einfallenden Strahlen sehen sagittal bzw.
meridional andere Krümmungsradien und werden an unterschiedlichen Brennpunkten fokussiert. Der Einfluß ist größer, je schiefer das Lichtbündel einfällt.
"
!
Bildfeldwölbung
14.4. LICHTLEITER
14.4
137
Lichtleiter
funktionieren mit Linsen oder Spiegeln, aber mit geringsten Verlusten unter
Verwendung von Glasfasern. Letztere nutzen die Totalreflektion
!
"
!
#
Die numerische Apertur einer optischen Faser beschreibt den maximalen
Winkel unter dem ein Lichtstrahl in eine Faser eintreten kann, um der Totalreflexion zu unterliegen:
q
N A = sin ✓a = n21 n22
Typisch für Glasfasern sind Werte n1 = 1.475 und n2 = 1.460. Daraus folgt ein
Wert von N A = 0.2, bzw. ✓a = 12o .
!
!
"
#
% &! "# "! ! '
! "# "! !
%
!
"
!
*
$
!
%
!
!
!
( ' )"
$ % &&'
$
%
In Graded-Index Optiken (GRIN) liegt eine kontinuierliche Variation von
n(r) vor. Damit folgen die Lichtstrahlen gekrümmten Trajektorien.
14.5
Geometrische Optik der Erdatmosphäre
Da die atmosphärische Dichte ⇢ mit der Höhe abnimmt, und in guter Näherung
n 1 / ⇢ = ⇢0 exp( r/8.3km) ist, verhält sich die Atmospäre wie ein GRIN
Medium. Der Fehler in der Position des Sternes nimmt mit dem Winkel vom
Zenith zu. Ebenfalls auf Grund der Dichteabnahme mit der Höhe über dem
Erdboden erfolgt eine Erweiterung der Sichtweite.
Fata Morgana
Ein starker Temperaturgradient in Bodennähe verkrümmt den Strahlengang
und das gesehene Objekt erscheint an anderer Stelle. Da Wellenfronten Punkte
gleicher Phase verbinden und der Ausbreitungsvektor senkrecht auf die
Wellenfront liegt, kann man folgenden Ansatz für den Krümmungsradius der Lichtbahn
! "# $ %& %' ( $ )
machen: Eine Bahn verläuft in einem Bereich mit Brechungsindex n über eine Wegstrecke r d'. Ein benachbarter Bereich hat
den Brechungsindex n + dn
dr dr. Diese Bahn
* "+ ,! - .%,"& %,"/ ,0 1 2 + / / 3 $ + ,4 3 ' 5 + '
durchquert zwischen zwei Phasenflächen die
Strecke (r + dr) d'. Da zwischen benachbarten Phasen-flächen die optischen Wegstrecken
gleich sind, muss gelten:
138
n r d' = (n +
dn
dr) · (r + dr) d' .
dr
In der Näherung, dass der Term mit dr2
vernachlässigbar ist, ergibt sich für den
Krümmungsradius
n
r=
.
dn/dr
( * !
+,- .
% * !
)
(
'
$ % "
$ &
$ %
!
#
"
!
#
&
$ !
Im homogenen Fall wird also der Radius 1.
Regenbogen
Beim Durchgang eines Lichtstrahls durch ein Wassertröpfchen in der Nähe des
geometrischen Zentrums kommt es zu einer geringen Stahlablenkung. In diesem
Bereich wird Licht im wesentlichen in Vorwärtsrichtung gestreut. Mit steigendem Abstand vom Zentrum erhöht sich die Ablenkung und gleichzeitig steigt
der beim Austritt ins Tröpchen zurückreflektierte Anteil der Strahlung. Strahlen, die nach einmaliger Reflexion aus dem Tröpchen austreten, konzentrieren
sich im wesentlichen um Ablenkwinkel von 180o 42o , nach zweimaliger Reflexion (und auf Grund des zusätzlichen Reflexionsverlustes schwächer) um Ablenkwinkel von 180o 51o . Der exakte Winkel hängt auf Grund der Dispersion des
Wassers von der Farbe ab. Unter diesen Winkeln sehen wir (vorausgesetzt die
Sonne steht hinter uns) zwei Regenbögen. Die Dispersion erscheint in den beiden
Bögen entgegengesetzt, innen rot. Eine genauere Behandlung (Airy 1838) zeigt,
dass in die Erscheinung des Regenbogens auf Grund von Beugung die Größe des
Tröpchens eingeht und die Interferenz der austretenden Strahlen berücksichtigt
werden muss.
#
!
( ) * * + * , -./ 0 1
2
"
( ) * * + * , -./ 0 1
"
!
#
$ % &
$ % &
$ ' &
Im Bild ist die Intensität jedes einzelnen
gebrochenen Strahles als gleich angenommen. In Wirklichkeit betonen die Fresnelschen Bedingungen (siehe Seite 127)
die Konzentration von intensiven Strahlen in den Ablenkbereich von 40-420 noch
stärker, als es bereits durch die Kaustik geschieht.
$ ' &
Caustics
Caustic
42o
Kapitel 15
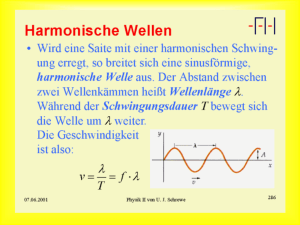
WELLENOPTIK
Die Grenzen zwischen geometrischer Optik (G.O.) und Wellenoptik zeigen sich
bei der Beleuchtung einer große Blende mit einem Parallelstrahl. Die Schattenfunktion projiziert im Sinne der G.O. ein Bild, das die Kontour der Blende
relativ genau nachzeichnet. Verringert man die Blendenö↵nung, dann verkleinert
sich anfänglich der Lichtfleck, bis die Helligkeitsverteilung wieder größer wird
und auf Grund von Interferenze↵ekten eine räumliche Modulation zeigt, die
nicht im Sinn der G.O. zu verstehen ist:
Licht erscheint unter Winkeln,
die nach der geometrischen Optik nicht zugänglich sind.
Poissons Punkt: Licht, wo es nach der geometrischen Optik, und nach der
ursprünglichen Korpuskeltheorie des Lichtes nicht sein dürfte. Die skalare
Fresnel-Kircho↵ ’sche Beugungstheorie ist ein Ansatz zum Verständnis dieser Beobachtungen. Man führt eine skalare Funktion ein, die Wellenfunktion U ,
die der Wellengleichung (11.3) genügt. Die genaue physikalische Bedeutung von
~ oder B
~ Feldes beschreiben.
U ist nicht spezifiziert, U könnte Komponenten des E
Das Ziel der Wellenoptik ist es die Welleneigenschaften und Strahleigenschaften in einem einfachen Konzept zu vereinigen. Die geometrische Optik ist
der Grenzfall der Wellenoptik für ! 0 und basiert auf folgenden Postulaten.
- Im homogenen, durchsichtigen Medium genügt eine einzige Konstante,
der reelle Brechungsindex n, wobei
uph = c/n .
(15.1)
- Die optische Welle wird durch die skalare Funktion U beschrieben, die der
linearen Wellengleichung genügt,
U=
1 @2U
.
u2ph @t2
(15.2)
- Die Superposition von Teilwellen gilt, da eine lineare Wellengleichung
vorliegt. Sind U1 (~r, t) und U2 (~r, t) Lösungen für optische Wellen, dann ist eine
weitere Lösung:
U (~r, t) = U1 (~r, t) + U2 (~r, t)
(15.3)
139
140
KAPITEL 15. WELLENOPTIK
- An Grenzflächen zwischen unterschiedlichen Medien ändert sich U , in einer
Weise, die vom Brechungsindex abhängt. Wie diese Änderung ist, hängt von
~ und
der spezifischen Bedeutung von U ab, Die Tangentialkomponenten von E
~
~
~
H sind stetig, Die Normalkomponenten von D und B sind stetig.
- In inhomogenen Medien kann man n(~r) und uph (~r) einführen, wenn die
Änderung des Brechungsindex über einen räumlichen Bereich erfolgt, der viel
größer ist als .
Die Verbindung der Funktion U mit (leicht) meßbaren Größen erfolgt über
• die optische Intensität [W/m2 ]
I(~r, t) = |U|2 (~r, t) .
(15.4)
Das zeitliche Mittel wird über ein Zeitintervall genommen, das viel größer
ist als die inverse optische Frequenz (bei 600 nm ist die Periode 2 fs ).
• die optische Leistung [W] ist die über eine Fläche
Z
P (t) =
I(~r, t) dS
(15.5)
S
integrierte Intensität. S liegt senkrecht zur Ausbreitungsrichtung.
• die optische Energie [J] ist die über die Zeit integrierte Leistung.
15.1
Monochromatische Wellen
sind unendlich ausgedehnt und werden durch eine wohldefinierte Frequenz !,
eine Amplitude a(~r) und eine Phase '(~r) bestimmt:
U (~r, t) = a(~r) cos (!t + '(~r)) .
(15.6)
Eine Vereinfachung ergibt sich durch die komplexe Darstellung
U (~r, t) = a(~r) ei!t ei'(~r) ,
(15.7)
bzw. nach Einführung der komplexen Amplitude u(~r) = a(~r) ei'(~r)
U (~r, t) = u(~r) ei!t .
(15.8)
In der komplexen Ebene rotiert der Zeiger u(~r) (im Englischen ”phasor”) mit der
optischen Frequenz. Sein Argument gibt die Phase, sein Betrag die Amplitude.
Mit diesem Ansatz wird aus der Wellengleichung die Helmholtz-Gleichung
+ k 2 u(~r) = 0 ,
(15.9)
wobei wir die Wellenzahl, k = ! n/c, verwendet haben.
Die optische Intensität ist dabei
I(~r) = |u(~r)|2 .
(15.10)
15.2. ELEMENTARWELLEN
15.2
141
Elementarwellen
Wir untersuchen einfache Lösungen der Helmholtz-Gleichung (15.9).
Ebene Welle
Mit der komplexe Amplitude A schreiben wir
u(~r) = A e
i~
k·~
r
= Ae
i(kx x+ky y+kz z)
.
(15.11)
Damit die Helmholtz-Gleichung erfüllt ist, muss für den Wellenvektor gelten
kx2 + ky2 + kz2 = k 2 . Die Intensität der Welle ist überall gleich I = |A|2 , sie trägt
unendlich hohe Leistung. Die Wellenfronten (Flächen konstanter Phase) sind
Ebenen senkrecht zu ~k.
Sphärische Welle
Mit r als Abstand von der Punktquelle schreiben wir
u(~r) =
A
e
r
ikr
.
(15.12)
Die Wellenfronten sind konzentrische Kugeln um die Punktquelle.
Paraboloidale Welle
Licht kann in Strahlen gebündelt, scheinbar räumlich lokalisiert und nahezu
divergenzfrei sich ausbreiten. Ebene und sphärische Wellen sind gerade das Gegenteil von Einengung der Divergenz und von räumlicher Lokalisation. Eine
Näherung zur beobachteten Bündelung stammt von von Fresnel. Sie gilt für eine sphärischen Welle in Gebieten, in denen ✓2 = (x2 + y 2 )/z 2 ⌧ 1 erfüllt ist,
r=
p
x2 + y 2 + z 2
=
⇡
✓
◆
✓2
✓4
1 + ✓2 = z 1 +
+
+ ...
2
8
✓
◆
2
2
2
✓
x +y
z 1+
=z+
.
2
2z
z
p
(15.13)
So folgt aus (15.12)
u(~r) ⇡
A
exp ( ikz) exp
z
✓
ik
x2 + y 2
2z
◆
.
(15.14)
Diese Näherung ist eine ebene Welle A e ikz , deren Wellenfronten durch den
Faktor in paraboloidische Wellenfronten, (x2 + y 2 )/z = const. gebogen werden.
Der Ursprung der Welle liegt bei z = 0, die Amplitude nimmt mit 1/z ab.
sphärisch
paraboloidisch
eben
142
KAPITEL 15. WELLENOPTIK
Diese Welle erfüllt die Helmholtz Gleichung in der paraxialen Näherung.
Diese Näherung gilt, wenn die ortsabhängige Amplitude A(~r) in einer Umgebung
der Größe etwa konstant ist,
@A
A
⌧
@z
@2A
A
⌧ 2.
2
@z
und
(15.15)
Die Normalen zur Wellenfront sind paraxiale Strahlen, die einhüllende Welle
ändert sich langsam über eine Distanz . Mit dem Ansatz u(~r) = A(~r) exp( ikz)
2
in der Wellengleichung 15.2 unter Vernachlässigung des Terms @@zA2 ergibt sich
die paraxiale Helmholtz-Gleichung
r2T A
i2k
@A
=0
@z
r2T =
wobei
@2
@2
+ 2.
2
@x
@y
(15.16)
In der Praxis wichtige Lösungen dieser Näherung sind Gaußsche Strahlen. Die
Strahlintensität eines Gaußschen Strahles konzentriert sich in einem kleinen Bereich um die Strahlachse, eine idealisierte Beschreibung eines Strahlenbündels
mit gaußförmigem Intensitätsverlauf in der Ebene senkrecht zur Ausbreitungsrichtung. Dazu wird die z-Koordinate in der Amplitude (15.14) durch z i z0
ersetzt, wobei der reelle Wert z0 die Position eines Minimums in der Strahltaille beschreibt. Im Gaußschen Strahl ergibt sich die optische
Intensität als eine
p
Funktion des Abstandes von der Strahlachse ⇢ = x2 + y 2 und der axialen
Position z,
I(⇢, z) = I0

W0
W (z)
2
exp

2⇢2
.
W 2 (z)
(15.17)
Für alle Werte z ist der Strahl eine Gauß-Funktion mit dem Maximum bei ⇢ = 0.
Die Krümmung der Wellenfront verschwindet im Fokusbereich. Die gesamte optische Leistung im Strahl ist
Z
1
P = I(⇢, z) 2⇡⇢ d⇢ = I0 (⇡W02 ) .
(15.18)
2
Die radiale Strahltaille ist definiert als der Wert von ⇢ bei dem die Intensität
auf den Wert von 1/e2 abgesunken ist, mit dem Fokusdurchmesser 2W0 ,
s
z2
W (z) = W0 1 + 2 ,
(15.19)
z0
Für z
z0 ist die Strahldivergenz ⇥0 =
⇡ W0 .
Die Raleigh-Länge (konfokaler
15.3. KOHÄRENZ
143
Parameter , Fokustiefe)
2z0 =
2⇡ W02
.
(15.20)
Phasenflächen eines Gaussschen Strahls,
der von links auf eine konventionelle Linse bzw. eine GRIN-Linse tri↵t.
Die kürzere Laufzeit der Welle durch den
Randbereich der Linse ist Ursache für die
Krümmung der Wellenfronten rechts von
der Linse.
15.3
Kohärenz
Für Interferenz müssen die interferierenden Teilwellen eine gewisse räumliche
und zeitliche Kohärenz aufweisen. Kohärenz beschreibt hier die Güte mit der
man zwei Wellenzüge als praktisch identisch ansehen kann.
Nahezu monochromatisches Licht wird von angeregten Atomen ausgesandt,
die einen Übergang zwischen zwei diskreten Energieniveaus (E2 E1 = h⌫)
machen. Der Übergang ist aber nicht wirklich scharf, denn mit der endlichen
Lebensdauer (⌧ ) des angeregten Zustandes ist eine natürliche Energieunschärfe
( E = h ⌫) verbunden, wobei ⌫ = ⌧ 1 ist. Damit enthält das Licht Beiträge
bei unterschiedlichen Wellenlängen (endliche Linienbreite), sodass nur quasimonochromatische Strahlung vorliegt. Im realen Fall wird diese Breite noch
weiter verschmiert, und zwar über den Doppler-E↵ekt und Energieverschiebungen durch die Wechselwirkung mit benachbarten Atomen.
Im Normalfall emittieren Atome unabhängig voneinander (statistisch), sodass keine feste Phasenbeziehung der Beiträge unterschiedlicher Atome zur Lichtwelle vorliegt. Eine Ausnahme bildet ein Laser.
Zeit
E2
Atom 1
E2
räumliche
Kohärenz
!"
Raum
E1
zeitliche Kohärenz
Atom 2
E1
Zur Beobachtung der Interferenz ist eine Beobachtungsdauer t notwendig und
damit besteht die Forderung, dass während der Zeit t sich die Phasenbeziehung zwischen den interferierenden Wellen nicht wesentlich ändert. Es ist also
eine zeitliche Kohärenz notwendig. Die Kohärenzzeit ist mit der Unschärfe
der Frequenz der Welle verbunden. Wenn mehrere Frequenzen in Bereich ⌫
vorhanden sind, dann ergibt sich nach einer Zeit t die Phasendi↵erenz
' = 2⇡
In der Zeit
⌫
t.
(15.21)
tcoh = 1/ ⌫ wächst die Phasendi↵erenz auf 2⇡. Während dieser
144
KAPITEL 15. WELLENOPTIK
Zeit läuft der Strahl über die Kohärenzlänge
Lcoh = c ·
tcoh .
(15.22)
Interferenzstrukturen können nur über ein Volumen
entsprechend der Größe der Kohärenzlänge beobachtet werden.
L1
L2
L1
Interferenzfähige Teilwellen aus
nur einer punktförmigen Lichtquelle
können über Spiegel erzeugt werden.
Identische Kopien der Lichtquelle
gehen von den virtuellen Quellen L1
und L2 aus. Im Fall rechts ist eine
erheblich größere Kohärenzlänge
erforderlich, um Interferenz am
Punkte P sichtbar zu machen.
Spiegel
L
L
P
P
15.4
Interferenz
Interferenz tritt auf, wenn zwei Wellen gleichzeitig am gleichen Ort sind.
Die gesamte Wellenfunktion ist gleich der Summe der einzelnen Wellenfunktionen. Es kommt zur Superposition der komplexen Amplituden. Das gilt
natürlich auch für mehr als zwei Wellen (Vielstrahlinterferenz). Wir untersuchen
zwei monochromatische Wellen u(~r) = u1 (~r) + u2 (~r) der Gesamtintensität
I
=
2
2
2
|u1 + u2 | = |u1 | + |u2 | + u⇤1 u2 + u1 u⇤2 .
Mit den Definitionen
p
u1 = I1 ei'1
und
u2 =
ergibt sich die Interferenzgleichung
p
I = I1 + I2 + 2 I1 I2 cos ' ,
p
(15.23)
I2 ei'2
(15.24)
(15.25)
wobei ' = '1 '2 ist. Die Abhängigkeit der Intensität von ' untersuchen wir
mit einem Zeigerdiagramm der Superposition. Für I1 = I2 erreicht die Gesamtintensität Maxima der vierfachen Einzelintensität, dazwischen liegt destruktive
Interferenz vor.
4
u1
3
u2
, 2
u
u2
1
M
4 S 2 S
0
M
2S
4S
u1
M2
M1
15.4. INTERFERENZ
145
Interferenz ebener Wellen unter kleinem Winkel
Bei Fresnel’scher Spiegelversuch (Seite 144) erzeugen zwei Spiegel oder ein Biprisma zwei kohärente, virtuelle Lichtquellen. Breite Bereiche der Wellenfront
werden so überlagert und erzeugen lichtstarke Interferenz. In einer vereinfachten
Beschreibung nehmen wir zwei ebene Wellen in der x-z Ebene:
p
I0 e ikz ,
u1 =
p
I0 e ik(z cos ✓+x sin ✓) .
(15.26)
u2 =
x
x
✓
✓
z
z
In der Ebene z = 0 ist die Phasendi↵erenz in (15.25) ' = kx sin ✓ und die
Intensität
|u1 + u2 |2 = 2 I0 [1 + cos(kx sin ✓)] .
(15.27)
Ein Interferenzmuster erscheint entlang der x-Achse mit einer Periode, die größer
ist als die Wellenlänge , nämlich
⇤ = /sin ✓ .
(15.28)
Die Periode kann über den Winkel ✓ kontrolliert werden. Das ist eine Methode
um feine Linien photolithographisch zu drucken; z.B. Brechungsgitter. Mit einem Laser (kohärente Lichtquelle) und Strahlteilern ist diese Interferenz präzise
über große Raumbereiche realisierbar.
Interferenz an planparalleler Platte
Der Gangunterschied zwischen reflektierten Teilstrahlen beträgt
p
s = 2d n2 sin2 ↵
(15.29)
"
#
!
und ihre Phasendi↵erenz
'=
2⇡
s.
(15.30)
Beträgt die Phasendi↵erenz ein ganzahliges Vielfaches von 2⇡ dann verstärken sich die Amplituden und erzeugen ein Interferenzmuster. Analog ist die Interferenz an einer keilförmigen Platte (in Reflexion oder Transmission) zu verstehen,
sowie die Farbgebung bei den sogenannten Newtonschen Ringen wie sie bei den nicht parallellen
Glasplatten, bei Ölfilmen oder bei Seifenlamellen
beobachtet werden..
!
"
% &' (
!
$
% &' (
#
146
KAPITEL 15. WELLENOPTIK
Mach-Zehnder Interferometer
Die Überlagerung zweier ebener Wellen nach
Durchlaufen unterschiedlich langer Arme z
und z d
p
u1 =
I0 e ikz
p
u2 =
I0 e ik(z d)
(15.31)
"
'
&
#
&
führt bei Veränderung der optischen Weglänge
d zu einer Intensitätsmodulation

2⇡d
|u1 + u2 |2 = 2 I0 1 + cos(
) . (15.32)
&
'
"
#
%
&
$
%
!
Analoges gilt für das Michelson und Jamin Interferometer.
% &' ( ) &' **+
'
) $ * + , - .$ / / 0 * $ *
& 1 .$ 2 $ %
(
'
$
Michelson
Interferometer
"
(
" # $ %%$
!
&
Jamin
Interferometer
7
9$ + 4$ *
& 1 .$ 2 $ %
8
"
#
$
!
3 $ 4$ 5 46 *
% &' ( ) &' **+
Sagnac-Interferometer
Dieses Interferometer erlaubt es Rotationsgeschwindigkeiten sehr exakt zu vermessen (technische Bedeutung als optisches Gyroskop für die Navigation). Zwei
Teilstrahlen laufen ringförmig um ein Zentrum mit einem Radius R (z.B. in
einer Glasfaser). Der optische Weg für einen Umlauf ist L = 2R⇡. Die tangentiale Geschwindigkeit ist v = R ⌦, wobei ⌦ die Rotationsgeschwindigkeit ist.
Für ⌦ = 0 ist die Umlaufszeit
⌧=
2⇡R
.
c
(15.33)
Im rotierenden Fall haben rechtsund links-umlaufende Strahlen einem um s± = R ⌦ ⌧± geringeren bzw. längeren Weg umzulaufen,
nämlich c+ ⌧+ = L + R ⌦⌧+ und
c ⌧ = L R ⌦⌧ , also ist
. %/ 0 1 $
" # $ %%$
!
, ,
&
⌧+
=
⌧
=
L
c+ R ⌦
L
c +R⌦
' $ ($ ) (* +
Nach dem relativistischen Additionstheorem für Geschwindigkeiten
c+ =
c+v
1 + v/c
c =
c v
1 v/c
(15.34)
15.4. INTERFERENZ
147
ist die Zeitdi↵erenz
⌧ = ⌧+
⌧ =
2LR⇡⌦
4⇡R2 ⌦
⇡
.
2
2
R ⌦
c2
(15.35)
c2
Die Zeitdi↵erenz ist also proportional zur Rotationsfrequenz und zur eingeschlossenen Fläche A = ⇡R2 . Diese Zeitdi↵erenz kann in eine Phasenverschiebung umgesetzt werden. Das Gyroskop verwendet die Lichtfrequenz !, damit
ist die Phasenverschiebung
'=! ⌧ =
2⇡c 4⇡R2 ⌦
.
c2
(15.36)
Mit einer analogen Anordnung hat Fizeau 1859 die Lichtgeschwindigkeit in
strömendem Wasser vermessen.
Vielstrahl-Interferenz
Wenn wir M Wellen gleicher Amplitude und gleicher
Phasendi↵erenzen
p
um = I0 ei(m 1)'
(15.37)
überlagern, addieren sich die Beiträge m = 1, 2, ...M
mit der Abkürzung h = ei' zur Gesamtamplitude
X
um =
m
!
!
!
!
p
p 1 hM
I 0 1 + h + h2 + h3 + . . . = I 0
.
1 h
!
I0
I0
I0
I0
I0
!
(15.38)
Die Gesamtintensität ist dann
I = I0
sin2 M '/2
.
sin2 '/2
(15.39)
Bei der Bragg-Reflektion an einem Kristall hat man M parallele reflektierende Netzebenen. Der Abstand d der Ebenen kontrolliert über den Eingangswinkel die Phasenverschiebung zwischen benachbart reflektierten Strahlen, '.
An jeder Netzebene wird ein nur sehr kleiner Anteil reflektiert, damit ist die
Primärintensität in jeder Ebene etwa gleich.
Interferenz von Wellen progressiv kleinerer Intensität
Bei Vielfachreflexion überlagern sich unendlich
viele Wellen mit immer kleiner werdender Amplitude und konstanter Phasendi↵erenz, sodass
h = r ei'
ist. Dann wird
X
p
um = I0
m
1
1
h
=
p
I0
1
woraus sich die Gesamtintensität als
1
r ei'
148
KAPITEL 15. WELLENOPTIK
I = I0
r)2
(1
1
1
= I0
.
2
+ 4r sin '/2
1 + (2F/⇡)2 sin2 '/2
(15.40)
ergibt. Die Finesse F ist definiert als
p
F = ⇡ r/(1 r) .
(15.41)
Dieser Fall tritt beim Fabry-Perot-Interferometer bzw bei einem Laserresonator
auf. Die Transmission zeigt periodische Resonanzen. Die Kombination dreier solcher Interferometer findet z.B. Anwendung zur präzisen Wellenlängenbestimmung.
1
10!3
0.8
r$0.2
0.6
Finesse
#
0.4
10!2
0.5
0.2
10!1
0.7
0.9
0
0
Π
2Π
3Π
4Π
0.5
0.6
0.7
"
0.8
0.9
1
r
Antireflexbeschichtung
Auf einem Substrat mit Brechungsindex n3 ist eine dünne
dielektrische Schicht mit Brechungsindex n2 der Dicke d
aufgebracht. Auf die dünne Schicht tri↵t ein Lichtstrahl, der
an der ersten und zweiten Grenzfläche teilweise reflektiert
wird. Der Unterschied der optischen Weglängen der beiden
reflektierten Wellen
! #
! "
! #
! "
s = 2n2 d
! #
! "
führt zur destruktiven Interferenz, wenn
! $
'=
2⇡
0
s = (2m + 1)⇡
also n2 d =
% & ' ( )*+ )
0
4
Die Auslöschung des reflektierten Lichtes optimiert, wenn auch die Amplituden
der Strahlen (1) und (2) gleich groß sind. Dazu muß man beachten, daß 1 viele
Reflexionen (mit progressiv kleinerer Intensität) zu den Strahlen (1) und (2)
beitragen. Die Amplituden berechnet man aus den Fresnel’schen Gleichungen.
p
Optimiert ist die dünne Schicht, wenn n2 = n1 n3 ist. Für ein Substrat aus
Glas n3 = 1.5 und den Übergang aus Luft n1 = 1 ergibt sich n2 = 1.225.
Umgekehrt kann man die Reflexion optimieren, in dem man periodische Mehrschichtsysteme verwendet für dielektrische Spiegel (oder Filter) mit sehr
hoher Reflektivität (Transmission) in einem schmalen Wellenlängenbereich.
!
"
4
Dazu eignen sich im sichtbaren Bereich die Ma! 01 0$ 23 3 #
+
' ,$
terialien MgF2 (n = 1.38) und TiO2 (n = 2.40),
&
%
$ ,+
wobei bis zu 20 Doppelschichten aufgetragen wer#
den. Der Reflexionskoeffizient kann dann in einem
*
$ ,%
)
bestimmten Wellenlängenbereich, für bestimmten
(
$ ,*
Einfallswinkel(bereich) und Polarisation auf Wer'
"
te von R = 99.99 % gebracht werden.
% $ $
& $ $
# $ $
! "-. /
15.4. INTERFERENZ
149
Interferenz zwischen zwei sphärischen Wellen
Zwei sphärische Wellen entstehen phasengleich von den Orten S1 und S2 und
interferieren auf einem Schirm, z.B. in einer Ebene parallel zu den Quellen.
Wenn die zwei Punktquellen in Phase emittieren entstehen Intensitätsmaxima
im Raum, wenn immer die Abstandsdi↵erenz zu den Quellen r1 r2 ein Vielfaches von 2⇡/ ist. Diese Bedingung r1 r2 = m 2⇡/ ist die Erzeugende für
Hyperboloide, die wir nach der Zahl m klassifizieren können. Gezeigt ist der Fall
in dem der Abstand d der beiden Punktquellen 5 < d < 6 beträgt. 5 Hyperboloide auf denen die Phasendi↵erenz der Wege |r1 r2 | = m ein ganzzahliges
Vielfaches m der Wellenlänge beträgt zeigenkonstruktive Interferenz.
Zwei sphärische Wellen
gleicher Intensität starten
von den Orten {±a, 0, 0}
und interferieren in der
Ebene z = d. In der parabolischen Approximation
gilt ✓ = 2a/d und für die
Intensitätsverteilung

2⇡x ✓
I(y, x, d) = 2 I0 1 + cos(
) .
(15.42)
Intensitätsmaxima erscheinen mit der Periode
x = /✓.
Weisslichtinterferenz
Diese Interferenz entsteht auch aus 2 kohärenten Quellen von weißem Licht.
Wenn die jeweiligen Farbbeiträge zueinander eine feste Phasenbeziehung haben,
interferieren Rot mit Rot, Blau mit Blau. Es resultiert ein weißes Interferenzmuster (verwaschen).
Kohärente Lichtquellen können auch über Beleuchtung zweier Ö↵nungen mit
einer inkohärenten Lichtquelle erreicht werden. Diese inkohärente Lichtquelle
habe die Größe b ⇥ b. Die einzelnen Flächenelemente dieser Quelle emittieren
Licht mit statistisch verteilten Phasen. Solange diese Schwankungen bei den
Ö↵nungen S1 und S2 synchron ankommen, liegt eine feste Phasenbeziehung vor
und die aus S1 und S2 ausgehenden Wellen können miteinander interferieren.
Ein Strahl aus dem Zentrum der Quelle läuft
gleich weit bis S1 und S2. Dieser Beitrag liefert eine feste Phasenbeziehung. Strahlen von R1 nach
S1 und von R1 nach S2 haben Gangunterschied
,
$
#
s = b sin ↵ = b a/D
&
'
!
!
Phasenkorrelierte Beleuchtung beider Ö↵nungen
durch eine inkohärente Quelle liegt vor, wenn:
$
!
#
"
%
)* !
! (
,
2a
D
⌧
b
+
bisher: Interferenz von ebenen Wellen, Strahlen bzw. Punktquellen,
in der Folge: Interferenz von ausgedehnten Quellen (Beugung)
%
150
KAPITEL 15. WELLENOPTIK
15.5
Beugung
Damit bezeichnen wir die Ablenkung eines Lichtstrahls an begrenzenden Ö↵nungen. Schon sehr früh beschrieben, Grimaldi 17. Jht.”di↵ractio”, Maraldi 18.Jht,
Arago 1820. Dieser E↵ekt ist Schallwellen, Lichtwellen und Materiewellen gemeinsam. Er tritt immer auf, wenn ein Teil der Wellenfront irgenwie behindert
wird. Der E↵ekt ist besonders stark bemerkbar, wenn das Hindernis (oder die
Ö↵nung) in der Größenordnung der Wellenlänge ist. Zum Beispiel gehen Schallwellen um große Hindernisse (500 Hz entsprechen 68 cm).
Eine anschauliche Beschreibung gibt das Fresnel-Huygens’sche-Prinzip: Jeder Punkt der eingeschränkten Wellenfront ist Urspung sphärischer Wellen (sekundäre Elementarwellen). Die Interferenz dieser Elementarwellen ergibt das
Beugungsmuster.
Die landläufige Definition beschreibt die Überlagerung einer überschaubaren
Zahl von Teilwellen als Interferenz. Bei Beugung überlagern sich sehr viele
Wellen aus einem kontinuierlichen Gebiet. Beugung ist wichtig, weil optische
Elemente immer nur einen Teil der Wellenfront verwenden. Die damit verbundene Beugung beschränkt das Auflösungsvermögen optischer Instrumente.
Fraunhofer-Beugung: beugendes Element ist sehr klein im Vergleich zum Abstand zum Beobachtungspunkt (dieser ist im Unendlichen).
Fresnel-Beugung: Beobachtung in der Umgebung des beugenden Elementes
(Nahfeldbereich).
Beugungsmuster am Einzelspalt
Eine ebene Welle tri↵t auf einen Schirm mit spaltförmiger Ö↵nung der Breite
D. Jeder Punkt im Spalt ist eine Quelle für eine sekundäre Elementarwelle.
p Für
m kohärente Quellen im Abstand d, von denen jede die Amplitude I0 /m
aussendet, ist die Intensität unter dem Winkel ↵ durch die Gleichung (13.8),
Seite 121) gegeben. Mit d = m · d wird daraus
⇥
⇤
I0 sin2 ⇡ d sin ↵
I0
sin2 x
⇥
⇤
I(↵) = 2
=
(15.43)
2
d
m sin ⇡ m
m2 sin2 [x/m]
sin ↵
Lassen wir m ! 1 gehen, erhalten wir sin[x/m] ⇡ x/m, wobei x = sin ↵ k d/2
ist. Mit der sinc Funktion, sinc x = sinx x , ist das Beugungsmuster
lim I(↵) = I0
m!1
sin2 x
= I0 sinc2 x .
x2
(15.44)
1
! "# $%
sinc2 x
0.8
!
!
"
0.6
0.4
!
!
!
0.2
0
!3Π !2Π
# $ % &' (
!Π
0
x
Π
2Π
3Π
15.5. BEUGUNG
151
Beugung an einer Kante
Mathematischer Hintergrund:
Cornu’sche Spirale
Beugung an kreisförmiger Ö↵nung
Für eine kreisförmige Ö↵nung (Durchmesser
d) tritt anstelle der Sinusfunktion die Besselfunktion erster Ordnung, J1 (x), auf (AiryMuster ). Wenn ebene Welle auf einen Schirm
mit kreisförmiger Ö↵nung vom Durchmesser
D tri↵t, entsteht ein Beugungsbild mit einem
zentralen Maximum.
Das zentrale Maximum liefert eine Scheibe hoher Intensität (Airy-Scheibe). Die
erste Nullstelle von J1 (x) tritt bei x = 3.83 und liefert den Radius der AiryScheibe als
⇢1 = 1.22
f·
.
d
(15.45)
Die Airy Scheibe stellt eine fundamentale Grenze für die Schärfe einer Abbildung
durch Beugung dar. Die Schärfe steigt mit dem Durchmesser d der Linse. Sie
ist umso besser, je kleiner Wellenlänge und Brennweite sind.
Werden zwei Lichtpunkte (Sterne) mit einer Linse abgebildet, dann erzeugt
jeder Punkt ein Airy-Muster. Am Beobachtungsschirm sind die beiden Airy
Scheibchen noch trennbar, wenn der Abstand zwischen ihren Zentren
dmin
2.44 f · /d
(15.46)
ist, also ihr Winkelabstand
↵min = dmin /(2 f ) = 1.22 /d
(15.47)
nicht unterschreitet. Bei diesem Winkelabstand hat die Überlagerung der zwei
Besselfunktionen noch ein erkennbares Minimum.
Beugungsgitter
Jetzt untersuchen wir N parallele Spalte in der Ebene z = 0. Die Einzelspaltbreite ist d, Abstand der Spalte ist G. In jedem Spalt tritt Beugung auf. Die
gebeugten Lichtbündel aus den N Spalten interferieren miteinander,
⇥
⇤
I0 sin2 ⇡ G sin ↵
sin2 x
⇥
⇤
I(↵) = 2
·
,
(15.48)
N sin2 ⇡ N G sin ↵
x2
wobei x = sin ↵ k d/2. Das entspricht dem Signal durch die Interferenz der N
Spalte mal dem Beugungsmuster am Einzelspalt.
152
KAPITEL 15. WELLENOPTIK
4
4
3
3
2
2
1
1
&
(
!
!
!
0
40
20
0
20
Mikrometer
40
0
150 100 50
0
50
Mikrometer
100
150
&
! "# $% "!
'
Maxima treten auf, wenn der Gangunterschied aus benachbarten Spalten ein
Vielfaches der Wellenlänge ist:
s = d · sin ↵ = m ·
(15.49)
Wie groß diese Maxima werden hängt vom ersten Faktor ab. Die Beugung (der
zweit Faktor) ist dafür verantwortlich, daß überhaupt Licht in die Richtung
abgelenkt wird, um zu interferieren. Ein solches Gitter ist realisierbar in Transmission durch N Spalte, bzw. in Reflexion an N kleinen Flächen eines Gitters
Beugung am Vielfachspalt wurde auch mit Materiewellen gezeigt:
Mit Neutronen (1975), He-Atomen (1991), He3 -Molekülen (1997), und mit einem Bose-Einstein Kondensat (1998). Gezeigt ist hier das Ergebnis des Experimentes aus Konstanz (Kurtsiefer, Pfau und Mlynek, Nature 386, 150, 1997)
in dem das zeitliche Anwachsen des Interferenzmusters in Folge des Auftre↵ens
einzelner Atome deutlich sichtbar wird.
) * + ! '
! " # $ %& ' (
%2
3
, - .( " )
( & - /0 "
( 0 /" " 1
Zonenplatte
Wir teilen eine sphärische Wellenfront
in kreisförmige Zonen, die entstehen,
wenn wir sie mit Kugeln schneiden, deren Zentrum bei einen Beobachter in
P liegt, und deren Radien sich gera" $ !
de um den Wert von /2 unterscheiden. Die erste Kugel berührt die Wel" $ ! %&
lenfront im Abstand r0 . Die nächste
"
!
Schnittfläche erfolgt für den Radius von
r0 + /2, u.s.w. Die dabei entstehenden
ringförmigen Zonen auf der Wellenfront
heissen Fresnelzonen.
Für jede Punktquelle in einer Fresnelzone, gibt es einen in der benachbarten
Zone, dessen Abstand von P gerade um /2 größer ist. Jede Quelle aus einem ringförmigen Flächenelement innerhalb einer Zone liefert konstruktiven
Beitrag der sekundären Elementarwellen beim Punkt P . Beiträge aus benachbarten Fresnelzonen neigen dazu, sich auszulöschen, da ein Gangunterschied um
/2 vorliegt. Deckt man jede zweite Fresnelzone ab, so ergibt sich eine konstruktive Überlagerung (Linsenwirkung) bei P .
#
#
#
15.6. HOLOGRAPHIE
153
Wenn die Quelle ins Unendliche rückt, kann man eine
ebene Wellenfront ebenfalls in Fresnelzonen einteilen.
Die Radien der Zonen sind
p
p
rm = m r0 + m2 2 /4 ⇡ m r0 .
Damit entsteht eine Linse der Brennweite r0 . Entweder deckt man jede zweite Zone ab, oder man
führt ein Stufenmuster ein, sodass benachbarte Zonen einen optischen Gangunterschied von ⇡ beim
Durchlaufen der Zonenplatte erreichen.
Fresnel-Linse: eine konventionelle Linse, in der die Kugelkalotte durch Stufen
analoger Krümmung ersetzt ist. Sie realisiert eine großflächige dünne Linse.
15.6
Holographie
In der Photographie wird die 3D-Welt in 2D übersetzt. Am Film kommt es
zur punktweisen Aufzeichnung des Quadrates der elektrischen Feldstärke. Beobachtet wird die Intensität. Bei der konventionellen Photographie wird jeder
Objektpunkt auf einen Bildpunkt hin abgebildet. Die Phaseninformation geht
verloren, sie ist bei inkohärentem Tageslicht im Normalfall ohne Bedeutung.
In der Holographie (holos=ganz ) wird die Phaseninformation aufgezeichnet. Diese Aufzeichnung erlaubt die spätere 3D-Rekonstruktion des Objektes.
Erfunden von Denis Gabor (1947).
Aufnahme des Hologramms:
7 ' 8' #' - * 0 "#$ % &
! "# $ % &"' (&' #
Eine Laserlichtquelle mit Strahlteiler und Teleskop gibt 2 große Strahlen zur Beleuchtung des Objektes
und zur Beleuchtung des holographischen Films. Der zweite Strahl,
6 $ 0 ' #
die Bezugswelle, wird direkt auf eine Photoplatte gerichtet. Der erste
$ ) * + ) (&, ' - , ' #
Strahl beleuchtet das Objekt. Das
. ' / ' - 0 "$ - ,
vom Objekt ausgehende Wellenfeld
. ' / ' - 0 "$ - , 0 5
0 "#$ % &
ist in der räumlichen Verteilung sei) ' &(1 % "' "'
2 % 3 "3 / # $ 2 % (0 1 % '
ner Amplituden und Phasen geprägt
4 &$ ""'
durch die Struktur des Objektes.
Vom Objekt gestreute Wellenfeld tri↵t als Gegenstandswelle auf dieselbe Photopatte. Mehr noch: Die gesamte, vom Objekt ausgehende Streustrahlung wird auf
der Photoplatte registriert. Das Interferenzmuster der beiden Strahlen wird an
jedem Punkt der Photoplatte aufgezeichnet1 . Auf Grund der geometrischen Ausdehnung des Objektes treten erhebliche Gangunterschiede zwischen den interferierenden Lichtfeldern auf. Darin steckt die Phaseninformation des 3-D Bildes. Um diese Phaseninformation zu erhalten muss die Lichtquelle möglichst
kohärent (monochromatisch) und phasenstabil sein. Auch muss jede Bewegung
des Objektes bzw des Filmes wähernd der Aufnahme des Holograms unterbunden werden.
1 Aus diesem Grund kann man eine holographische Aufzeichnung zerschneiden und erhält
aus jedem Bruchstück ein gleiches, wenn auch unschärferes Bild.
154
KAPITEL 15. WELLENOPTIK
Die Referenzwelle tri↵t direkt auf die Photoplatte (bei r~0 = {x, y, 0})
i~
k0 ·~
r0
u 0 = A0 e
.
(15.50)
Die Gegenstandswelle hat auf der Photoplatte die ortsabhängige Amplitude
ug = Ag (x, y) ei'g (x,y) .
(15.51)
Die Reaktion des Filmes ist proportional zur lokalen Intensität
I(x, y)
=
=
2
|u0 + ug | = u20 + u2g + u0 u⇤g + u⇤0 ug
A20
+
A2g
+ 2A0 Ag cos ('0
(15.52)
'g (x, y)) .
(15.53)
Die relative Phase zwischen den beiden Strahlen an einem Punkt (x, y) der
Photoplatte hängt vom zusätzlichen Weg der Gegenstandswelle über alle Objektpunkte ab, die zu diesem Punkt (x, y) auf der Photoplatte hin abstrahlen.
Jetzt wird der Film so entwickelt, dass die Transmission des (durchsichtigen)
Filmes T (x, y) gerade der lokalen Intensität entspricht, unter anderem
T (x, y) / u0 u⇤g + u⇤0 ug .
(15.54)
' 1 )2 &. # ' +)'
3 / " )" 4 ( - 3 / &% . / '
5 +- ))' 67 8 " +" 4 ( - 9 9 :
* ' )(- . / )' (
Hologramm Rekonstruktion :
Die im Hologramm steckende Information kann in ein Bild des Objektes zurücktransformiert werden,
wenn ein Rekonstruktionsstrahl,
!" # $ % % &' ( )' %
* &+,
u r = Ar e
0 &( )$ ' ++' %
* &+,
i~
kr ·~
r0
,
(15.55)
mit den gleichen Eigenschaften wie bei der Aufnahme am Hologramm gebeugt
wird. Dabei entstehen drei Wellenfronten: die ungebeugte Welle, ein virtuelles
Bild des Phasengitters und ein reelles Bild. Die durch das Hologramm transmittierte Amplitude des Rekonstruktionsstrahls,
ut = T (x, y) ur ,
(15.56)
ist wegen (15.54) proportional zu ut / ur u0 u⇤g +ur u⇤0 ug . Sie enthält also neben
der geschwächten Rekonstruktionswelle auch Anteile mit
ur u0 u⇤g
ur u⇤0
ug
=
=
Ar A0 Ag (x, y)e
Ar A0 Ag (x, y)e
i(~
kr +~
k0 )·~
r0
i(~
kr ~
k0 )·~
r0
e
e
i'g (x,y)
i'g (x,y)
,
,
(15.57)
(15.58)
also Wellen, die in die Richtung ~kr ± ~k0 gebeugt werden. Diese entsprechen den
Richtungen unter denen das reelle bzw. virtuelle Bild entsteht.
SS 2014
ENDE