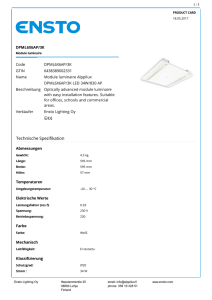
Wahrheitstafel für die logischen Operatoren

Wahrheitstafel für die logischen Operatoren
A
B
¬A
A∧B
A∨B
A→B
A↔B
false
false
true
false
false
true
true
false
true
true
false
true
true
false
true
false
false
false
true
false
false
true
true
false
true
true
true
true
Logik für Informatiker, SS ’06 – p.12
Uniforme Notation
Konjunktive Formeln:
Disjunktive Formeln:
Typ α
Typ β
Raymond Smullyan
Logik für Informatiker, SS ’06 – p.13
Uniforme Notation
Konjunktive Formeln:
Typ α
¬¬ A
A∧B
¬(A ∨ B)
¬(A → B)
Disjunktive Formeln:
Typ β
Raymond Smullyan
Logik für Informatiker, SS ’06 – p.13
Uniforme Notation
Konjunktive Formeln:
Typ α
¬¬ A
A∧B
¬(A ∨ B)
¬(A → B)
Disjunktive Formeln:
Typ β
¬(A ∧ B)
A∨B
A→B
Raymond Smullyan
Logik für Informatiker, SS ’06 – p.13
Uniforme Notation
Zuordnungsregeln Formeln / Unterformeln
α
α1
α2
A∧ B
A
B
¬(A∨ B) ¬ A ¬ B
¬(A→ B)
¬¬ A
A ¬B
A
A
Logik für Informatiker, SS ’06 – p.14
Uniforme Notation
Zuordnungsregeln Formeln / Unterformeln
α
α1
α2
A∧ B
A
B
¬(A∨ B) ¬ A ¬ B
¬(A→ B)
¬¬ A
A ¬B
A
β
β1
β2
¬(A∧ B) ¬ A ¬ B
A∨ B
A
B
A→ B ¬ A
B
A
Logik für Informatiker, SS ’06 – p.14
Uniforme Notation: Beispiel der Anwendung
Alternative Art der Definition von val I
val I (α) =


 true

 false
val I (β ) =


 true

 false
falls
val I (α1 ) = true und val I (α2 ) = true
sonst
falls
val I (β1 ) = true oder val I (β2 ) = true
sonst
Logik für Informatiker, SS ’06 – p.15
Uniforme Notation: Beispiel der Anwendung
Alternative Art der Definition von val I
val I (α) =


 true

 false
val I (β ) =


 true

 false
falls
val I (α1 ) = true und val I (α2 ) = true
sonst
falls
val I (β1 ) = true oder val I (β2 ) = true
sonst
Umfaßt Definition von val I für alle Operatoren außer:
1, 0, ¬, ↔
Logik für Informatiker, SS ’06 – p.15
Modell einer Formel(menge)
Definition: Modell einer Formel
Modell / Interpretation I ist Modell einer Formel A ∈ For0Σ , falls
val I (A) = true
Logik für Informatiker, SS ’06 – p.16
Modell einer Formel(menge)
Definition: Modell einer Formel
Modell / Interpretation I ist Modell einer Formel A ∈ For0Σ , falls
val I (A) = true
Definition: Modell einer Formelmenge
Modell / Interpretation I ist Modell einer Formelmenge M ⊆ For0 Σ , falls
val I (A) = true
für alle A ∈ M
Logik für Informatiker, SS ’06 – p.16
Zur Erinnerung: Logische Folgerbarkeit
Definition: Logische Folgerbarkeit
Formel A folgt logisch aus Formelmenge KB
gdw.
alle Modelle von KB sind auch Modell von A
Notation
KB |= α
Logik für Informatiker, SS ’06 – p.17
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
B ∨ ¬C
KB
α
Logik für Informatiker, SS ’06 – p.18
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
false
true
false
true
true
true
true
true
B ∨ ¬C
KB
α
Logik für Informatiker, SS ’06 – p.18
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
false
true
false
true
true
true
true
true
B ∨ ¬C
true
false
true
true
true
false
true
true
KB
α
Logik für Informatiker, SS ’06 – p.18
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
false
true
false
true
true
true
true
true
B ∨ ¬C
true
false
true
true
true
false
true
true
KB
false
false
false
true
true
false
true
true
α
Logik für Informatiker, SS ’06 – p.18
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
false
true
false
true
true
true
true
true
B ∨ ¬C
true
false
true
true
true
false
true
true
KB
false
false
false
true
true
false
true
true
α
false
false
true
true
true
true
true
true
Logik für Informatiker, SS ’06 – p.18
Ein erster Kalkül: Wahrheitstafelmethode
Beispielformel
α = A∨B
KB = (A ∨ C) ∧ (B ∨ ¬C)
Überprüfen ob KB |= α
A
false
false
false
false
true
true
true
true
B
false
false
true
true
false
false
true
true
C
false
true
false
true
false
true
false
true
A∨C
false
true
false
true
true
true
true
true
B ∨ ¬C
true
false
true
true
true
false
true
true
KB
false
false
false
true
true
false
true
true
α
false
false
true
true
true
true
true
true
Logik für Informatiker, SS ’06 – p.18
Logische Äquivalenz
Definition: Logische Äquivalenz
Zwei Formeln sind logisch äquivalent,
wenn sie in den gleichen Modellen wahr sind, d.h.
α |= β and β |= α
Logik für Informatiker, SS ’06 – p.19
Logische Äquivalenz
Definition: Logische Äquivalenz
Zwei Formeln sind logisch äquivalent,
wenn sie in den gleichen Modellen wahr sind, d.h.
α |= β and β |= α
Notation
α≡β
Logik für Informatiker, SS ’06 – p.19
Logische Äquivalenz
Definition: Logische Äquivalenz
Zwei Formeln sind logisch äquivalent,
wenn sie in den gleichen Modellen wahr sind, d.h.
α |= β and β |= α
Notation
α≡β
Beispiel
(A → B)
≡
(¬ B → ¬ A)
(Kontraposition)
Logik für Informatiker, SS ’06 – p.19
Logische Äquivalenz
Substitutionstheorem
Wenn
A≡B
C 0 ist das Ergebnis der Ersetzung einer Unterformel A in C durch B,
dann
C ≡ C0
Logik für Informatiker, SS ’06 – p.20
Logische Äquivalenz
Substitutionstheorem
Wenn
A≡B
C 0 ist das Ergebnis der Ersetzung einer Unterformel A in C durch B,
dann
C ≡ C0
Beispiel
A∨B
≡
B∨A
impliziert
(C ∧ (A ∨ B)) → D
≡
(C ∧ (B ∨ A)) → D
Logik für Informatiker, SS ’06 – p.20
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∧
Kommutativität von ∨
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
Assoziativität von ∧
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
• ((A ∨ B) ∨ C) ≡ (A ∨ (B ∨ C))
Assoziativität von ∧
Assoziativität von ∨
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
Assoziativität von ∧
• ((A ∨ B) ∨ C) ≡ (A ∨ (B ∨ C))
Assoziativität von ∨
• (A ∧ A) ≡ A
Idempotenz für ∧
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
Assoziativität von ∧
• ((A ∨ B) ∨ C) ≡ (A ∨ (B ∨ C))
Assoziativität von ∨
• (A ∧ A) ≡ A
• (A ∨ A) ≡ A
Idempotenz für ∧
Idempotenz für ∨
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
Assoziativität von ∧
• ((A ∨ B) ∨ C) ≡ (A ∨ (B ∨ C))
Assoziativität von ∨
• (A ∧ A) ≡ A
Idempotenz für ∧
• (A ∨ A) ≡ A
Idempotenz für ∨
• ¬¬ A ≡ A
Doppelnegation
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A ∧ B) ≡ (B ∧ A)
Kommutativität von ∧
• (A ∨ B) ≡ (B ∨ A)
Kommutativität von ∨
• ((A ∧ B) ∧ C) ≡ (A ∧ (B ∧ C))
Assoziativität von ∧
• ((A ∨ B) ∨ C) ≡ (A ∨ (B ∨ C))
Assoziativität von ∨
• (A ∧ A) ≡ A
Idempotenz für ∧
• (A ∨ A) ≡ A
Idempotenz für ∨
• ¬¬ A ≡ A
• (A → B) ≡ (¬ B → ¬ A)
Doppelnegation
Kontraposition
Logik für Informatiker, SS ’06 – p.21
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
Elimination Implikation
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
• (A ↔ B) ≡ ((A → B) ∧ (B → A)
Elimination Implikation
Elimination Äquivalenz
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
Elimination Implikation
• (A ↔ B) ≡ ((A → B) ∧ (B → A)
Elimination Äquivalenz
• ¬(A ∧ B) ≡ (¬ A ∨ ¬ B)
de Morgans Regeln
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
Elimination Implikation
• (A ↔ B) ≡ ((A → B) ∧ (B → A)
Elimination Äquivalenz
• ¬(A ∧ B) ≡ (¬ A ∨ ¬ B)
• ¬(A ∨ B) ≡ (¬ A ∧ ¬ B)
de Morgans Regeln
de Morgans Regeln
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
Elimination Implikation
• (A ↔ B) ≡ ((A → B) ∧ (B → A)
Elimination Äquivalenz
• ¬(A ∧ B) ≡ (¬ A ∨ ¬ B)
de Morgans Regeln
• ¬(A ∨ B) ≡ (¬ A ∧ ¬ B)
de Morgans Regeln
• (A ∧ (B ∨ C)) ≡ ((A ∧ B) ∨ (A ∧ C)) Distributivität von ∧ über ∨
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen
• (A → B) ≡ (¬ A ∨ B)
Elimination Implikation
• (A ↔ B) ≡ ((A → B) ∧ (B → A)
Elimination Äquivalenz
• ¬(A ∧ B) ≡ (¬ A ∨ ¬ B)
de Morgans Regeln
• ¬(A ∨ B) ≡ (¬ A ∧ ¬ B)
de Morgans Regeln
• (A ∧ (B ∨ C)) ≡ ((A ∧ B) ∨ (A ∧ C))
Distributivität von ∧ über ∨
• (A ∨ (B ∧ C)) ≡ ((A ∨ B) ∧ (A ∨ C))
Distributivität von ∨ über ∧
Logik für Informatiker, SS ’06 – p.22
Wichtige Äquivalenzen (zusammengefasst)
(A ∧ B)
(A ∨ B)
((A ∧ B) ∧ C)
((A ∨ B) ∨ C)
(A ∧ A)
(A ∨ A)
¬¬ A
(A → B)
(A → B)
(A ↔ B)
¬(A ∧ B)
¬(A ∨ B)
(A ∧ (B ∨ C))
(A ∨ (B ∧ C))
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
≡
(B ∧ A)
(B ∨ A)
(A ∧ (B ∧ C))
(A ∨ (B ∨ C))
A
A
A
(¬ B → ¬ A)
(¬ A ∨ B)
((A → B) ∧ (B → A))
(¬ A ∨ ¬ B)
(¬ A ∧ ¬ B)
((A ∧ B) ∨ (A ∧ C))
((A ∨ B) ∧ (A ∨ C))
Kommutativität von ∧
Kommutativität von ∨
Assoziativität von ∧
Assoziativität von ∨
Idempotenz für ∧
Idempotenz für ∨
Doppelnegation
Kontraposition
Elimination Implikation
Elimination Äquivalenz
de Morgans Regeln
de Morgans Regeln
Distributivität von ∧ über ∨
Distributivität von ∨ über ∧
Logik für Informatiker, SS ’06 – p.23
Wichtige Äquivalenzen mit 1 und 0
• (A ∧ ¬ A) ≡ 0
Logik für Informatiker, SS ’06 – p.24
Wichtige Äquivalenzen mit 1 und 0
• (A ∧ ¬ A) ≡ 0
• (A ∨ ¬ A) ≡ 1
Tertium non datur
Logik für Informatiker, SS ’06 – p.24
Wichtige Äquivalenzen mit 1 und 0
• (A ∧ ¬ A) ≡ 0
• (A ∨ ¬ A) ≡ 1
Tertium non datur
• (A ∧ 1) ≡ A
Logik für Informatiker, SS ’06 – p.24
Wichtige Äquivalenzen mit 1 und 0
• (A ∧ ¬ A) ≡ 0
• (A ∨ ¬ A) ≡ 1
Tertium non datur
• (A ∧ 1) ≡ A
• (A ∧ 0) ≡ 0
Logik für Informatiker, SS ’06 – p.24
Wichtige Äquivalenzen mit 1 und 0
• (A ∧ ¬ A) ≡ 0
• (A ∨ ¬ A) ≡ 1
Tertium non datur
• (A ∧ 1) ≡ A
• (A ∧ 0) ≡ 0
• (A ∨ 1) ≡ 1
Logik für Informatiker, SS ’06 – p.24
Ein zweiter Kalkül: Logische Umformung
Definition: Äquivalenzumformung
(Wiederholte) Ersetzung einer (Unter-)Formel durch
äquivalente Formel
Anwendung des Substitutionstheorems
Logik für Informatiker, SS ’06 – p.25
Ein zweiter Kalkül: Logische Umformung
Definition: Äquivalenzumformung
(Wiederholte) Ersetzung einer (Unter-)Formel durch
äquivalente Formel
Anwendung des Substitutionstheorems
Theorem
Äquivalenzumformung bildet mit den aufgelisteten
wichtigen Äquivalenzen einen vollständigen Kalkül:
Wenn A, B logisch äquivalent sind, kann A in B umgeformt werden
Logik für Informatiker, SS ’06 – p.25
Allgemeingültigkeit
Definition: Allgemeingültigkeit
Eine Formel ist allgemeingültig, wenn sie in allen Modellen wahr ist
Logik für Informatiker, SS ’06 – p.26
Allgemeingültigkeit
Definition: Allgemeingültigkeit
Eine Formel ist allgemeingültig, wenn sie in allen Modellen wahr ist
Notation
|= A
Logik für Informatiker, SS ’06 – p.26
Allgemeingültigkeit
Definition: Allgemeingültigkeit
Eine Formel ist allgemeingültig, wenn sie in allen Modellen wahr ist
Notation
|= A
Beispiele
A ∨ ¬A
A→A
(A ∧ (A → B)) → B
1
Logik für Informatiker, SS ’06 – p.26
Deduktionstheorem
Deduktionstheorem
KB |= A
gdw.
KB → A ist allgemeingültig
(verbindet logische Folgerbarkeit und Allgemeingültigkeit)
Logik für Informatiker, SS ’06 – p.27
Deduktionstheorem
Deduktionstheorem
KB |= A
gdw.
KB → A ist allgemeingültig
(verbindet logische Folgerbarkeit und Allgemeingültigkeit)
Folgerungen
M ∪ { A} |= B gdw. M |= A → B
A, B sind logisch äquivalent
gdw.
A ↔ B ist allgemeingültig
Logik für Informatiker, SS ’06 – p.27
Erfüllbarkeit
Definition: Erfüllbarkeit
Eine Formel ist erfüllbar, wenn sie ein Modell hat
Logik für Informatiker, SS ’06 – p.28
Erfüllbarkeit
Definition: Erfüllbarkeit
Eine Formel ist erfüllbar, wenn sie ein Modell hat
Beispiele
A∨B
A
A ∧ (A → B)
Logik für Informatiker, SS ’06 – p.28
Unerfüllbarkeit
Definition: Unerfüllbarkeit
Eine Formel ist unerfüllbar, wenn sie in keinem Modell wahr ist, d.h.,
nicht erfüllbar ist
Logik für Informatiker, SS ’06 – p.29
Unerfüllbarkeit
Definition: Unerfüllbarkeit
Eine Formel ist unerfüllbar, wenn sie in keinem Modell wahr ist, d.h.,
nicht erfüllbar ist
Beispiel
A ∧ ¬A
Logik für Informatiker, SS ’06 – p.29
Allgemeingültigkeit / Ableitbarkeit / Unerfüllbarkeit
Theorem
A ist allgemeingültig
gdw.
¬ A ist unerfüllbar
(verbindet Allgemeingültigkeit und Unerfüllbarkeit)
Logik für Informatiker, SS ’06 – p.30
Allgemeingültigkeit / Ableitbarkeit / Unerfüllbarkeit
Theorem
A ist allgemeingültig
gdw.
¬ A ist unerfüllbar
(verbindet Allgemeingültigkeit und Unerfüllbarkeit)
Theorem
KB |= A
gdw.
(KB ∧ ¬ A) ist unerfüllbar
(verbindet logische Ableitbarkeit und Unerfüllbarkeit)
Logik für Informatiker, SS ’06 – p.30
Verbindung der Eigenschaften
Aus den Theoremen folgt
Logische Folgerbarkeit
Allgemeingültigkeit
Unerfüllbarkeit
sind verbunden.
Kalkül für eine dieser Eigenschaften genügt
Logik für Informatiker, SS ’06 – p.31