Thermodynamik und Relaxationserscheinungen

J. M E I X N E R
und meiner Werte bei MgS0 4 mußte nach dieser
theoretischen Überlegung dadurch herbeigeführt
worden sein, daß in beiden Fällen Wasser verwendet worden war mit etwa gleicher Verunreinigung durch denselben Nichtelektrolvten. Es war
anzunehmen, daß das Wasser durch längeres
Stehen mit Luft gesättigt war und so eine Verfälschung des Kurvenverlaufes der Funktion
ig (V c) entstand. Erneute Versuche mit frisch
destilliertem, entlüftetem Wasser ergaben jetzt in
der Tat statt der s-förmigen xp ( k / c)-Kurven die
bekannten Jones-Dole-Geraden. F ü r MgS0 4 sind
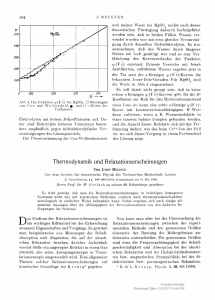
die Werte in Abb. 4 eingezeichnet.
Abb. 4. Die Funktion xp(V c) bei MgS0 4 . O Messungen
von C o x und W o l f enden 2 ,
und(X)-Werte des
Verfassers.
Elektrolyten mit hohem B-Koeffizienten auf. Daher sind Elektrolyte höheren Valenztyps besonders empfindlich gegen nichtelektrolvtische Verunreinigungen des Lösungsmittels.
Die Übereinstimmung der Cox-Wolfendenschen
Es soll damit nicht gesagt sein, daß es keine
echten s-förmigen xp {V c)-Kurven gibt. Da der BKoeffizient ein Maß für den Hvdratationszustand
eines Ions ist, kann eine echte s-förmige ip (V r)Kurve mit konzentrationsabhängigem B - Wert
dann auftreten, wenn z. B. Wassermoleküle in
einer inneren Sphäre komplex gebunden werden,
und die Anzahl dieser Moleküle sich mit der Verdünnung ändert, wie das beim Cr 3 +-Ion der Fall
ist, wo sich dieser V o r g a n g in einem Farbwechsel
der L ö s u n g zeigt.
Thermodynamik und Relaxationserscheinungen
Von
JOSEF MEIXNER
Aus dem Institut für theoretische Physik der Technischen Hochschule Aachen
(Z. N a t u r f o r s c h g . 4 a. 594—600 [104«)]; e i n g e g a n g e n a m 18. Mai 1940)
Herrn Prof. Dr. W. Ger lach zu seinem 60. Geburtstage gewidmet
Es wird gezeigt, daß man die Relaxationserscheinungen in beliebigen homogenen
Systemen nicht nur mit kinetischen Methoden, sondern auch thermodynamisch-phänomenologisch in einfacher Weise behandeln kann. Dabei ergeben sich auch einige allgemeine Aussagen über die Abhängigkeit der Relaxationszeiten von den äußeren Bedingungen des Systems.
D
as Studium der Relaxationserscheinungen ist
ein wichtiges Hilfsmittel bei der Erforschung
atomarer Eigenschaften und Vorgänge. So gewinnt
man beispielsweise aus Messungen der Schallabsorption und -dispersion, die auf der akustischen Relaxation beruhen, darüber Aufschluß,
wieviel Stöße ein angeregtes Molekül in einem Gas
überlebt, ehe seine Anregungsenergie in Translationsenergie umgewandelt wird. Eine allgemeine
Theorie solcher Relaxationserscheinungen auf
kinetischer Grundlage hat K r ö n i g 1 gegeben.
Nun kann man aber bei der Untersuchung der
Relaxationserscheinungen zwischen der experimentellen Methode und den gemessenen Größen
einerseits, der Deutung der Meßergebnisse andererseits unterscheiden. Die gemessenen Größen
sind etwa die Frequenzabhängigkeit der Schallgeschwindigkeit und Absorption bei der akustischen Relaxation und der Dielektrizitätskonstanten bzw. magnetischen Permeabilität bei der dielektrischen bzw. paramagnetischen Relaxation.
1 R. de L. K r o n i g ,
Physik. Z. 39, 823 [1938],
Dieses Werk wurde im Jahr 2013 vom Verlag Zeitschrift für Naturforschung
in Zusammenarbeit mit der Max-Planck-Gesellschaft zur Förderung der
Wissenschaften e.V. digitalisiert und unter folgender Lizenz veröffentlicht:
Creative Commons Namensnennung-Keine Bearbeitung 3.0 Deutschland
Lizenz.
This work has been digitalized and published in 2013 by Verlag Zeitschrift
für Naturforschung in cooperation with the Max Planck Society for the
Advancement of Science under a Creative Commons Attribution-NoDerivs
3.0 Germany License.
Zum 01.01.2015 ist eine Anpassung der Lizenzbedingungen (Entfall der
Creative Commons Lizenzbedingung „Keine Bearbeitung“) beabsichtigt,
um eine Nachnutzung auch im Rahmen zukünftiger wissenschaftlicher
Nutzungsformen zu ermöglichen.
On 01.01.2015 it is planned to change the License Conditions (the removal
of the Creative Commons License condition “no derivative works”). This is
to allow reuse in the area of future scientific usage.
THERMODYNAMIK
UND
RELAXATIONSERSCHEINUNGEN
Es handelt sich also durchwegs um phänomenologische Größen und um Meßmethoden aus dem Bereich der phänomenologischen Physik. Solange
man von einer atomtheoretischen Deutung der
Meßergebnisse absieht, sollte also auch eine
phänomenologische Beschreibung des den Messungen zugrunde liegenden V o r g a n g s möglich sein.
Man muß aber von vornherein abgrenzen, was
man in diesem Sinne unter einer atomtheoretischen
Deutung verstehen will. AVenn man eine chemische
Reaktionsgleichung anschreibt, so stecken in Unnatürlich auch gewisse atomphysikalische Kenntnisse. Sie bestehen darin, daß die Reaktionsgleichungen ganzzahlige Koeffizienten haben, wenn
man die umgesetzten Mengen in den Größen mißt,
die man als Mole bezeichnet. Doch ist dieser Umstand nicht notwendig für eine phänomenologische
Theorie; er kann hier vielmehr als zufällig betrachtet wrerden. Im übrigen können wir uns die
umgesetzten Mengen der einzelnen Reaktionspartner auch in Gramm ausgedrückt denken, dann ist
diese Ganzzahligkeit in den Reaktionsgleichungen
latent geworden. Daß überhaupt Reaktionsgleichungen mit bestimmten Koeffizienten existieren,
ist aber eine phänomenologische
Erfahrung, ebenso wie die Tatsache, daß es chemische Reaktionen
gibt.
Etwas schwieriger zu beantworten ist die Frage,
ob man die Prozesse der Dissoziation, Ionisation
und Anregung, welche sich ja alle formal durch
chemische Reaktionsgleichungen beschreiben lassen, phänomenologisch erfassen kann. A u c h hier
ist zu unterscheiden zwischen dem, wTas man unter
diesen Prozessen atomtheoretisch versteht, und
der Frage, ob sich solche Prozesse in phänomenologischen Untersuchungen äußern. Z u r Klärung
der letzten Frage brauchen wir aber nur ein einziges Beispiel anzuführen, nämlich die Umwandlung zwischen Para- und Orthowasserstoff, die,
atomtheoretisch gesehen, im Übergang von A\7asserstoffmolekülen mit geraden Rotationsquantenzahlen in solche mit ungeraden besteht. A u c h wenn
man keine Atomtheorie hätte, könnte man durch
phänomenologische Untersuchungen eine Umwandlung des AVasserstoffs feststellen, z. B. aus
der Änderung der spezif. AA'ärmen bei gewissen
Operationen, und für diese Umwandlung eine Reaktionsgleichung mit einer wohldefinierten Reaktionswärme aufstellen.
Bei der Analyse der möglichen Reaktionen
eines gegebenen Systems wird man auf atomtheo-
595
retische Überlegungen nicht verzichten können.
1st jedoch der Mechanismus, der einem beobachteten Relaxationsvorgang zugrundeliegt, nicht bekannt, so kann eine thermodynamische Analyse
unter Ansatz einer oder mehrerer, zunächst nicht
näher präzisierterReaktionen vonNutzen sein und
für die kinetische Deutung einen Fingerzeig geben.
Auch bei Systemen, die nicht aus näherungsweise unabhängigen Teilsystemen bestehen, und
für welche die Theorie von Kronig in der gegebenen Form daher nicht mehr anwendbar ist
(kooperative Phänomene), läßt sich das thermodynamische Verfahren unverändert durchführen.
Schließlich sind auch, wTorauf wir aber hier nicht
näher eingehen wollen, Systeme mit Konvektion.
AVärmeleitung und Diffusion, aber auch Systeme
mit mehreren Phasen (etwa Relaxation der Verdampfung) der thermodynamischen Behandlung
zugänglich.
Unser Ziel wird also sein, eine thermodynamisch-phänomenologische Theorie der Relaxationserscheinungen als Gegenstück zur kinetischen
Theorie von Kronig zu entwickeln. Dabei beschränken wir uns auf homogene Substanzen, in
welchen beliebige Reaktionen ablaufen können.
Unter Reaktionen verstehen wir die eigentlichen
chemischen Reaktionen, Dissoziation, Assoziation, Ionisation und Anregung, also Übergänge
zwischen verschiedenen Energieniveaus der einzelnen Molekülarten uswr. Der Aggregatzustand
kann ein beliebiger sein; doch nehmen wir ihn
der Einfachheit halber isotrop an.
1. D i e t h e r m o d y n a m i s c h e n
lagen
Grund-
AVir betrachten also ein homogenes System, in
welchem n voneinander unabhängige Reaktionen
ablaufen können. Das Volumen pro Gramm sei F,
der Druck p, die Temperatur T. Der chemische
Zustand sei durch die Reaktionslaufzahlen y 1 ,
y 2 , . . . y„ beschrieben; sie geben an, wie oft jede
der einzelnen Reaktionen von einem fest gewählten, von V und T unabhängigen Bezugszustand
aus abgelaufen ist. V o n einem Materieaustausch
des Systems mit der Umgebung sei abgesehen.
U und S seien die innere Energie und die Entropie
pro Gramm. Dann gilt für ihre Differentiale bei
einer infinitesimalen Zustandsänderung
M
dU = LTdT + (Kv+1/)
dV+
£
i -1
(K' + L)d7i,
(1)
J. M E I X N E R
596
TdS = LTdT+Lv
dV + ^Vdy..
(2)
«=i
Die Arbeitskoeffizienten K und die Wärmekoeffizienten L hängen von den Veränderlichen
V, T,y1, y 2 , . . . yn und im übrigen von den Parametern, welche den Bezugszustand charakterisieren, ab. Da die Veränderlichen Arbeitskoordinaten sind, so konnten wir KT = 0 setzen. Ferner ist
K
(3)
— —P •
Die Bedingungen für das chemische Gleichgewicht folgen etwa aus der Minimumseigenschaft
der freien Energie F=U
— TS mit den Nebenbedingungen dT = 0, dV = 0. Sie lauten:
Ä ' ( 7 \ V;
, . . . , yn) = 0
(i=
1,2,...,»)
Form in den yt— y., d.h. in den Abweichungen
der Reaktionslaufzahlen vom Gleichgew r ichtswert
gegeben. W i r wollen annehmen, daß das chemische
Gleichgewicht für alle T, V stabil ist und daß
alle Reaktionen wirklich ablaufen, also keine
Hemmungen vorliegen. Dann ist die quadratische
Form in (8) positiv definit, da im stabilen Gleichgewicht die freie Energie ein absolutes Minimum hat.
A u s (5) folgt, daß man die yk — yk auch linear
durch die K' ausdrücken kann; wir setzen
n
7, -
7,. = ^ B, k Kk
k= 1
(1 = 1 , 2 , . . . , » . ) ,
wobei die B i k ebenfalls die Eigenschaft
(4)
B
und stellen n Gleichungen zur Bestimmung der
Gleichgewichtswerte yä der yj in Abhängigkeit
von T und V dar. In der Nähe des Gleichgewichts
können wir daher die K { in folgender Weise
durch die ersten Glieder einer Taylor-Reihe darstellen:
ik=Bki
</,A-= 1 . 2 , . . . , « )
F(T,g;
yL , . . . y )
(11)
n
k= 1
gewichtswerte Yj einzusetzen sind. A u s den Differentialbeziehungen (1) und (2) folgt übrigens
die
(G)
und wenn wir diese Größen für den Gleichgewichtsfall mit bik(T,V)
abkürzen, so gilt also
=
hki
(«,*= 1,2,..,»).
(7)
Ebenso können wir die freie Energie bei festem
T,V in der Umgebung des Gleichgewichts in einer
Taylor-Reihe nach den yk — yk entwickeln; wregen
dF = ZK1 dyt bei festem T, V folgt mit Hilfe
von (5):
F(T,V;
yl,...,
+
Yn) = F (T,V;y
n
n
i =l k- 1
u
i=l jfc=l
wobei in dem Koeffizienten dK'/dyk die Gleich-
hik
<10)
besitzen. Man kann daher die freie Energie in der
Umgebung des chemischen Gleichgewichts auch
nach den Arbeitskoeffizienten Kl entwickeln und
erhält auf ähnliche Weise wie oben
n
dKl
(9)
...,
yj
(8)
Die Abweichung der freien Energie vom Gleichgewichtswert ist also durch eine quadratische
Die Abweichung der freien Energie vom Gleichgewichtswert ist hier durch eine quadratische
Form in den Arbeitskoeffizienten K{ ausgedrückt.
Auch diese quadratische F o r m ist positiv definit.
Dieser quadratischen F o r m für die freie Energie
stellen wir nun eine andere quadratische Form
für die lokale Entropieerzeugiing bzw. Energiedissipation gegenüber.
A u s (1) und (2) folgt für die zeitliche Änderung der Entropie
«
TdS/dt = dU/dt +pdV/dt
— £ K' dy./dt.
i=i
(12)
Die Entropie im System ändert sich also durch
die Energiezufuhr von außen, abzüglich der
Volumenarbeit, und durch die im System verlaufenden chemischen Reaktionen. Der letzte A n teil hat die Gestalt einer Summe von Produkten
aus Arbeitskoeffrzient und zugehöriger Reaktionsgeschwindigkeit. Bei geringen
Abweichungen
vom chemischen Gleichgewicht läßt sich jede
Reaktionsgeschwindigkeit als lineare Funktion
aller Arbeitskoeffizienten ausdrücken mit Koeffi-
THERMODYNAMIK
zienten aiV
UND
R E L A X A TI 0 N S E R S C H E I N U N G E N
597
welche nur von T und V abhängen.
cl y
(« = 1 , 2 , . . , » ) ,
"
(17)
k=\
worin die y , aik und B jk nun Konstanten sind.
Nach Elimination der y i erhält man hieraus
wobei das Prinzip der mikroskopischen Reversibilität, oder, in der Sprache der Chemiker,
das Prinzip des detaillierten chemischen Gleichgewichts verlangt, daß die Onsagerschen Reziprozitätsbeziehungen
aik
=
aki
(*» * = 1 , 2 , . . , n)
(14)
gelten 2 . Dieser lineare Ansatz gilt immer, gleichgültig. ob es sich um Reaktionen erster oder
höherer Ordnung handelt, und ob die zugrundegelegten Reaktionen unabhängige Elementarreaktionen oder irgendwelche unabhängige Kombinationen von solchen sind.
Setzt man (13) in (12) ein, so ergibt sich als
Energiedissipation pro Gramm ( = lokale Entropieerzeugung pro Gramm multipliziert mit
T),
welche durch die chemischen Reaktionen hervorgerufen wird.
i=l
<
i'=l
i 5
>
Sie ist nach dem zweiten Hauptsatz positiv und
verschwindet, falls keine Hemmungen vorliegen,
nur, wenn alle Kl verschwinden, d. h. im chemischen Gleichgewicht. A l s o ist auch diese Energiedissipation eine positiv definite quadratische F o r m
der Arbeitskoeffizienten K>.
2. I s o t h e r m e R e l a x a t i o n b e i
stantem Volumen
K k
(*'=!,2,..,n),
(16)
Vgl. zu (13) und (14) J. M e i x n e r , Z. physik.
Chem., Abt. B 53, 235 [1943], Ann. Physik (5) 43, 244
[1943]. Dort findet sich auch weitere Literatur.
j.rk
U
('=1.2,..,«).
(18)
Dies ist ein System von n unabhängigen linearen
Differentialgleichungen mit konstanten Koeffizienten. Letztere gehören zu zwei positiv definiten
quadratischen Formen (11) und (15) und besitzen
die Symmetrieeigenschaften (10) und (14).
Statt die Gin. (16) und (17) in ihrer allgemeinen
Form zu integrieren, kann man versuchen, sie
durch eine Transformation der Reaktionsgleichungen in eine einfachere Form zu bringen. Man
kann ja die Reaktionsgleichungen miteinander
linear kombinieren, so daß neue Reaktionsgleichungen mit den Reaktionslaufzahlen
«
V,i='ESitVt'
d e t
i U * °
(*' = 1 , 2 , . . , n)
(19)
entstehen. Sie sind zur Beschreibung des V o r ganges ebenso gut geeignet wie die ursprünglichen. Die £4fc können hierbei willkürliche reelle
Koeffizienten sein. Die n unabhängigen Reaktionen, wrelche zu den y- gehören, brauchen dabei
keine unmittelbar anschauliche Bedeutung im
chemischen Sinne von Elementarreaktionen zu
haben. F ü r die neuen Arbeitskoeffizienten K v
und Wärmekoeffizienten Lv gilt dann
n
kon-
W i r setzen jetzt als äußere Bedingungen für
den Ablauf der Reaktionen voraus, daß das
Volumen und die Temperatur festgehalten werden; letzteres erfordert, daß die entstehende Reaktionswärme in geeigneter Weise abgeführt
wird. F ü r den zeitlichen Ablauf der Reaktionen
gilt dann nach (9) und (13):
- dy
- - ä r = Z,ai*
&=i
H
=
n
=
(20)
wie man leicht aus den für konstante T, V geltenden Beziehungen 2 K'dy/ = 2K[' dy] und 2 L ' dy{
= 2L1' dy\ folgern kann 3 .
Es läßt sich nun stets eine Transformation der
ursprünglichen Reaktionen, d.h.ein Koeffizientenschema
finden, so daß in den neuen Reaktionslaufzahlen die Gin. (16) und (17) die besonders
einfache Gestalt
= Y
2
3
K
''' y l - h =
Ki
'
<«=i.2,..,»)(21)
J. M e i x n e r, Ann. Physik (5) 43, 244 [1943].
J. M E 1 X X E R
598
haben. Wie P r i g o g i n e 4 bemerkt hat. ist eine
solche Transformation mit konstanten Koeffizienten l j k im allgemeinen nicht möglich; sie werden
von der Temperatur und vom Volumen abhängig
sein. d. h. die transformierten Reaktionsgleichungen sind bei jeder Temperatur und bei jedem
Volumen andere. Doch hat dies auf unsere Überlegungen. bei denen T und V konstant angenommen werden, keinen Einfluß.
Die Transformation, welche auf die einfachen
Gin. (21) führt, ist, mathematisch gesprochen,
nichts anderes als die gleichzeitige Hauptachsentransformation der beiden positiv definiten quadratischen Formen (11) und (15). Sie gehen dabei
über in
n
n
1 / 2 2 K'
i 1
bzw.
K'
Yj R i
i=-1
•
(")
Da sie auch in der transformierten Form positiv
definit sein müssen, folgt unmittelbar, daß alle 7,
reell und positiv sind. Die %i lassen sich als "Wurzeln der Determinantengleichung
det
— ra.J
(23)
.
1k
1 ki= 0
\ /
berechnen.
Die Integration der Differentialgleichungen (21)
ist nun sehr einfach und liefert
.
y\ -
= OY -
0
• "
l i
(»"=1.2..,»).
(24)
Jede der transformierten Reaktionslaufzahlen y\
nähert sich also exponentiell mit einer ihr eigenen Relaxationszeit r, ihrem Gleichgewichtswert y\. Wegen (19) gilt dann für die ursprünglichen Reaktionszahlen yi. daß jedes yt — y) ein
W JAggregat von n Exponentialfunktionen e
'mit
reellen Koeffizienten ist. Daraus folgt nach allgemeinen Sätzen über solche Aggregate von Exponentialfunktionen 5 , daß bei beliebiger Wahl der
unabhängigen Reaktionsgleichungen und bei beliebigen Anfangsbedingungen (welche aber nicht
zu weit von den Gleichgewichtswerten liegen dürfen) jedes y, höchstens (n — l)-mal durch seinen
Gleichgewichtswert hindurchgeht und höchstens
n — 1 Extremalwerte annimmt. — Dieser Satz
wurde zusammen mit dem oben gewonnenen Satz,
daß die Relaxationszeiten reell und positiv sind,
mit etwas anderen Überlegungen von J o s t 0 für
Systeme von Reaktionen erster Ordnung und für
gewisse Systeme mit Reaktionen erster und zweiJ. P r i g o g i n e ,
(5) 32.30 ll946|.
4
Bull. Acad. rov. Sei. Belgique
ter Ordnung bewiesen. Unser Beweis gilt für
Systeme mit Reaktionen beliebiger Ordnung in
der Umgebung des chemischen Gleichgewichts.
3. A d i a b a t i s c h e R e l a x a t i o n
bei k o n s t a n t e m V o l u m e n
W i r setzen jetzt als äußere Bedingungen für
den Ablauf der Reaktionen voraus, daß das
Volumen festgehalten wird und kein Wärmeaustausch mit der Umgebung stattfindet. Dann bleiben
die Beziehungen (13) und (14) für die Reaktionsgeschwindigkeiten bestehen. A u s (1) folgt wegen
dU = 0,dV = 0
dT _ _
dt
A
A"' + Jj dr i _ _ A
2J
' jT
(ft ~
Ij
Lr
dy^
dt '
'
Hierin können wir K'
0 setzen, da wir wieder
geringe Abweichungen vom chemischen Gleichgewicht voraussetzen, und daher die K i klein
gegen die L' sind.
Infolge des verhinderten Wärmeaustausches mit
der Umgebung wird die Temperatur nicht konstant bleiben, aber sich bei den vorausgesetzten
geringen Abweichungen vom chemischen Gleichgewicht auch nur wenig ändern. Sie wird also
stets in der Nähe einer festen Temperatur bleiben,
die wir mit T 0 bezeichnen wollen. Dann können
wir statt (5) entwickeln
K'
(T,
V;
, . . . , yn)
= i j hkV0<
k=i
n [7k-
(26)
y,(T0,
V)] +
dfT
( T - 70) .
Nun ist nach den thermodynamischen Differentialbeziehungen dK'/dT
— L ' / T . Daher ergibt sich
aus (13) und (26)
"
dy
_
I" "
(7 — 7'0)J
(1 = 1 . 2 . . , » » ) .
(27)
Diese Gleichungen zusammen mit (25) sind
) i + l Differentialgleichungen zur Bestimmung
von y1,...,yu.T
als Funktionen der Zeit. In den
Koeffizienten air bkl und in den L ' kann in un5 Vgl. G. P o l y a
u. G. S z e g ü , Aufgaben und
Lehrsätze aus der Analysis, 2. Bd., S. 48. Berlin 1925.
« W. J o s t , Z. Naturforschg. 2a, 159 [1947],
UND R E L A X A T I O N S E R S C H E I N U N GE N
THERMODYNAMIK
serer Näherung für T die Temperatur T 0 eingesetzt werden.
Zur Integration dieser Differentialgleichungen
nehmen wir wieder an, daß als Reaktionslaufzahlen die zu T{), V gehörigen Reaktionslaufzahlen y. des letzten Abschnittes gewählt sind. Dann
werden alle bkl = 1 für k = l und = 0 für k =1= l
und au — 1/r,, aik = 0 für i 4= k. Somit geht (27)
über in
= -
T 0 ). (28)
Eine Lösung von (25) und (28) ist zeit unabhängig und stellt die Gleichgewichtswerte
=
+ ^
(T-T0) =
7 i
(T,n
(29)
zu irgendeiner von T etwas verschiedenen Temperatur T dar. Alle anderen Lösungen klingen
exponentiell ab. W i r finden spezielle solche L ö sungen durch den Ansatz
7; -
9i ( 7 0, V)]^
y'i(10, n = [7; (i =
•
,
1,2,..,«)
(30)
und erhalten durch Elimination der Temperatur
aus (25) und (28) das homogene Gleichungssystem
(y;
-
91) + i
j= l
v
(yj 1
yj) = o>
(31)
Die Determinante dieses Gleichungssystems muß
verschwinden. Ihre Ausrechnung gibt für o die
Gleichung
/= i
V L'
1
l
j
1
1
- = 0 .
1
o
(32)
Dies ist, nach Beseitigung aller Nenner, eine
Polynomgleichung in o. W i r wollen zunächst voraussetzen, daß alle xi voneinander verschieden
sind. Dann hat diese Polynomgleichung den
Grad n und daher ^Relaxationszeiten o1,
o0,..on
als Lösungen. F ü r sie gilt, wenn alle oL und ti
nach wachsender Größe geordnet sind.
0 < ai < ti < Oo < t2
batischer Relaxation bei konstanter Dichte nehmen alle Relaxationszeiten ab.
Zum Beweis hat man nur zu zeigen, daß in
jedem der Intervalle (0, r ^ , ( r 1 , r 2 ) . . . , (r„ _ , ,
ein Vorzeichenwechsel von f (o) eintritt. Das ist
aber sofort einzusehen. Am oberen Ende jedes
dieser Intervalle wird f (o) — — o o , am unteren
Ende dagegen beim ersten Intervall / (ö) — 1. bei
den übrigen f (o) —- + o o . Vorausgesetzt ist dabei
die selbstverständliche Eigenschaft LT' >0.
—
Derselbe Satz läßt sich auch für isotherme und
adiabatische Relaxation bei konstantem Druck
beweisen.
Zu jeder Relaxationszeit Ö, gehört ein Anfangszustand, der genau exponentiell mit dieser Relaxationszeit abklingt; der Reaktionsverlauf zu
einem beliebigen Anfangszustand läßt sich als
Summe aus einer Konstanten und einem Aggregat
von Exponentialfunktionen mit den Exponenten
— //öj, . . . —t/on darstellen, und auch hier gilt
wieder: Es gibt für jedes y t (nicht nur für jedes
y . ) höchstens n — 1 Durchgänge durch den endgültig erreichten Gleichgewichtswert und höchstens n — 1 extreme Werte. Dasselbe gilt für die
Temperatur T.
Sind nicht alle r, voneinander verschieden, so
sind in (33) an den entsprechenden Stellen Gleichheitszeichen einzuführen; zu einer m-fachen Relaxationszeit r i gehört eine ihr gleiche (m — l)-fache
Relaxationszeit o r Die Zahl der Nulldurchgänge
und der Extreme ist dann höchstens gleich der
Zahl der verschiedenen o- weniger Eins.
J j
(t= 1,2,..,«).
"
Ö99
< on<vn.
(33)
Das heißt beim Übergang von isothermer zu adia-
4. R e l a x a t i o n u n d ä u ß e r e
wirkungen
Ein-
Während wir bisher nur die Einstellung des chemischen Gleichgewichts untersucht haben, setzen
wir nun voraus, daß das Gleichgewicht durch eine
periodische äußere Einwirkung f = f0-e'()l
gestört wird, f kann etwa eine elektrische oder
magnetische Feldstärke bedeuten. Dann tritt zu
dU bzw. TdS in (1) und (2) noch ein Term
(.Kf + Lf)df bzw. Udf hinzu. Alle Arbeits- und
Wärmekoeffizienten, somit auch die Lage des
chemischen Gleichgewichts, werden im allgemeinen von f abhängen. Die Gin. (13) bleiben bestehen, doch sind auch die aik jetzt im allgemeinen
von f abhängig; wir brauchen dies aber nicht zu
berücksichtigen, wenn f hinreichend klein ist.
W i r entwickeln die rechte Seite von (13) in der
Umgebung von F 0 , T0 und von f = 0. Dann wird.
THERMODYNAMIK
600
UND
RELAXATIONSERSCHEINUNGEN
wenn wir nur die Glieder niedrigster Ordnung berücksichtigen:
nr
+
" S
t
t
0
"
( V - To) +
( « = 1 , 2 . . , »).
)
(34)
Die
sind die Gleichgewichtswerte der yL für
T — T0, V = V0, f = 0. Dieses Gleicliungssystem
enthält n + 2 Unbekannte, T—T0,V—V0
und
die yi — y\; wir brauchen also zu den w Gin. (34)
noch zwei weitere. Sie werden durch die äußeren
Bedingungen gegeben, unter denen die Reaktionen
ablaufen. Sei beispielsweise das Volumen konstant gehalten und der Wärmeaustausch des
Systems mit der Umgebung unterbunden, dann
ist V—V0 = 0 und dS/dt = 0. Die letzte Bedingung ist zwar nicht genau richtig, da ja bei dem
irreversiblen Reaktionsablauf die Entropie zunimmt. Doch ist die dadurch bedingte Entropiezunahme pro Zeiteinheit — 2 Kl dyjdt von zweiter Ordnung klein und kann in unserer Näherung
vernachlässigt werden.
Die L ö s u n g dieses Systems von linearen Differentialgleichungen mit praktisch konstanten
Koeffizienten läßt sich aus der erzwungenen
Schwingung mit der Frequenzabhängigkeit e'on
der Unbekannten und der allgemeinen Lösung der
homogenen Differentialgleichungen mit f — 0 aufbauen. Letztere haben wir in Abschn. 4 untersucht; sie ist eine Summe von abklingenden Exponentialfunktionen mit den Relaxationszeiten
o1, o 2 , . . . , on. Nach hinreichend langer Zeit bleibt
nur die erzwungene Schwingung übrig.
Eine Analyse der Differentialgleichung (34)
liefert für die erzwungene Schwingung Ausdrücke
der Form
k^l
Ein ähnlicher Ausdruck ergibt sich für die Temperaturschwankungen. Die Cik hängen nur von
T () und F ab und lassen sich ebenso wie die
Relaxationszeiten ok durch die Arbeits- und
Wärmekoeffizienten und die phänomenologischen
Koeffizienten aik ausdrücken.
Hätten wir als äußere Bedingungen etwa konstante Temperatur und konstantes Volumen gewählt, so würden sich für die yi — 7ii Ausdrücke
von derselben Struktur wie (35) ergeben, aber
mit anderen Werten der Koeffizienten Ct uK n d mit
den zu diesen äußeren Bedingungen gehörenden
Relaxationszeiten r x , r 2 , . . . , r„ des Abschnitts 3.
Etwas anders liegen die Verhältnisse bei der
akustischen Relaxation. Dort ist f — 0, und die
äußere Einwirkung beeinflußt direkt eine der Zustandsgrößen des Systems. Man setzt etwa V — F 0
proportional zu e'b)l und hat in (34) zusammen
mit der Bedingung dS/dt = 0 gerade n + 1 Gleichungen zur Berechnung von T — T0 und der
y i — y r A u s der Zustandsgleichung des Systems
ergibt sich dann die Druckschwankung p — p 0 .
ausgedrückt durch V — F 0 , und für das Quadrat
der komplexen Schallgeschwindigkeit v erhält man
schließlich in bekannter Weise
r2
'
_
-
y-2
w
_
p'2 P
Po
y^Vo'
{
}
F ü r ein System, in welchem nur eine einzige
Reaktion, gleich welcher Art, abläuft, ergibt
sich so
.
v* = vl + (rj — t d V d +
'
V o n der Wiedergabe der Einzelheiten der Rechnung sehen wir ab. In (37) ist
M f ),,••
(38)
In den Differentialquotienten von p und K ist
nach Ausführung der Differentiation der Gleichgewichtswert y(T ,V ) für y einzusetzen.
a ist der phänomenologische Koeffizient, welcher die Reaktionsgeschwindigkeit bestimmt, und
welcher nach (13) durch
dl
= - a ( T , V)K(T,V,y)
(39)
definiert ist. Bei K und y haben wir den Index
weggelassen, da wir nicht mehr verschiedene Reaktionen zu unterscheiden brauchen. Damit ist
die komplexe Schallgeschwindigkeit tatsächlich
durch rein thermodvnamische und phänomenologische Größen ausgedrückt.