Tutoraufgabe 1 (Prim): Aufgabe 2 (Prim): (4 Punkte)

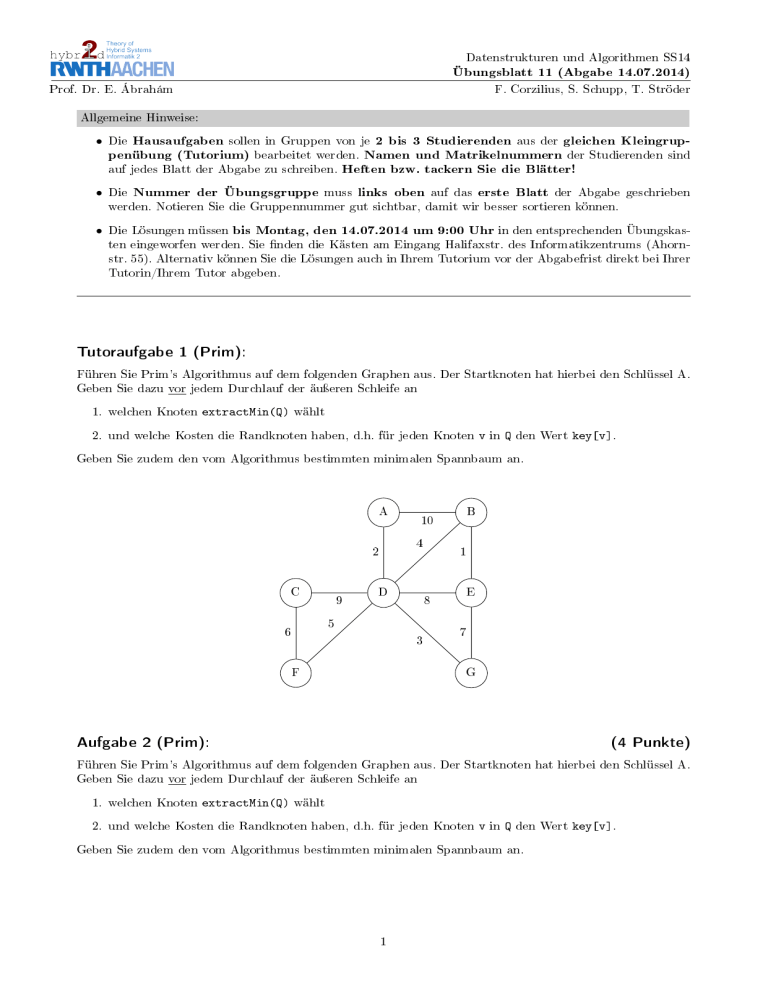
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
Prof.aa
Dr. E. Ábrahám
F. Corzilius, S. Schupp, T. Ströder
Allgemeine Hinweise:
• Die
sollen in Gruppen von je 2 bis 3 Studierenden aus der gleichen Kleingrupbearbeitet werden. Namen und Matrikelnummern der Studierenden sind
auf jedes Blatt der Abgabe zu schreiben. Heften bzw. tackern Sie die Blätter!
Hausaufgaben
penübung (Tutorium)
• Die
Nummer der Übungsgruppe muss links oben auf das erste Blatt der Abgabe geschrieben
werden. Notieren Sie die Gruppennummer gut sichtbar, damit wir besser sortieren können.
• Die Lösungen müssen
bis Montag, den 14.07.2014 um 9:00 Uhr in den entsprechenden Übungskasten eingeworfen werden. Sie nden die Kästen am Eingang Halifaxstr. des Informatikzentrums (Ahornstr. 55). Alternativ können Sie die Lösungen auch in Ihrem Tutorium vor der Abgabefrist direkt bei Ihrer
Tutorin/Ihrem Tutor abgeben.
Tutoraufgabe 1 (Prim):
Führen Sie Prim's Algorithmus auf dem folgenden Graphen aus. Der Startknoten hat hierbei den Schlüssel A.
Geben Sie dazu vor jedem Durchlauf der äuÿeren Schleife an
1. welchen Knoten extractMin(Q) wählt
2. und welche Kosten die Randknoten haben, d.h. für jeden Knoten v in Q den Wert key[v].
Geben Sie zudem den vom Algorithmus bestimmten minimalen Spannbaum an.
A
4
2
C
9
10
D
3
F
1
E
8
5
6
B
7
G
Aufgabe 2 (Prim):
(4 Punkte)
Führen Sie Prim's Algorithmus auf dem folgenden Graphen aus. Der Startknoten hat hierbei den Schlüssel A.
Geben Sie dazu vor jedem Durchlauf der äuÿeren Schleife an
1. welchen Knoten extractMin(Q) wählt
2. und welche Kosten die Randknoten haben, d.h. für jeden Knoten v in Q den Wert key[v].
Geben Sie zudem den vom Algorithmus bestimmten minimalen Spannbaum an.
1
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
A
B
1
5
7
8
2
E
C
6
10
D
4
3
F
G
9
Tutoraufgabe 3 (Floyd/Warshall):
Betrachten Sie den folgenden Graphen:
A
B
D
E
C
F
Führen Sie den Algorithmus von Warshall auf diesem Graphen aus. Geben Sie dazu nach jedem Durchlauf
der äuÿeren Schleife die aktuellen Entfernungen in einer Tabelle an. Die erste Tabelle enthält bereits die Adjazenzmatrix nach Bildung der reexiven Hülle. Der Eintrag in der Zeile i und Spalte j gibt also an, ob es eine
Kante vom Knoten der Zeile i zu dem Knoten der Spalte j gibt.
A
B
C
D
E
F
A
A
true true false false true false
A
B
true true true false false false
B
C
false false true false true false
C
D
true false false true false false
D
E
false true false false true false
E
F
false false false true false true
F
2
B
C
D
E
F
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
A
B
C
D
E
F
A
A
B
B
C
C
D
D
E
E
F
F
A
B
C
D
E
F
A
A
B
B
C
C
D
D
E
E
F
F
A
B
C
D
E
A
B
C
D
E
F
A
B
C
D
E
F
F
A
B
C
D
E
F
Aufgabe 4 (Floyd/Warshall):
(7 Punkte)
Betrachten Sie den folgenden Graphen:
A
1
B
1
7
4
E
C
2
2
5
4
D
2
F
3
3
G
Führen Sie den Algorithmus von Floyd auf diesem Graphen aus. Geben Sie dazu nach jedem Durchlauf der
äuÿeren Schleife die aktuellen Entfernungen in einer Tabelle an. Die erste Tabelle enthält bereits die Adjazenzmatrix nach Bildung der reexiven Hülle. Der Eintrag in der Zeile i und Spalte j ist also ∞, falls es keine
Kante vom Knoten der Zeile i zu dem Knoten der Spalte j gibt, und sonst das Gewicht dieser Kante. Beachten
3
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
Sie, dass in der reexiven Hülle jeder Knoten eine Kante mit Gewicht 0 zu sich selbst hat.
A
B
C
D
E
F
G
A
0
1
∞
∞
∞
∞
∞
A
B
∞
0
2
∞
7
∞
∞
B
C
∞
∞
0
4
∞
2
∞
C
D
∞
∞
∞
0
∞
∞
∞
D
E
1
4
5
∞
0
∞
∞
E
F
∞
∞
∞
∞
2
0
3
F
G
∞
∞
∞
∞
∞
3
0
G
A
B
C
D
E
F
G
A
A
B
B
C
C
D
D
E
E
F
F
G
G
A
B
C
D
E
F
G
A
A
B
B
C
C
D
D
E
E
F
F
G
G
4
A
B
C
D
E
F
G
A
B
C
D
E
F
G
A
B
C
D
E
F
G
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
A
B
C
D
E
F
G
A
A
A
B
B
C
C
D
D
E
E
F
F
G
G
B
C
D
E
F
G
Tutoraufgabe 5 (FordFulkerson):
Betrachten Sie das folgende Flussnetzwerk mit Quelle s und Senke t:
A
3
4
s
5
B
t
7
2
6
1
3
C
Berechnen Sie den maximalen Fluss in diesem Netzwerk mithilfe der Ford-Fulkerson Methode. Geben Sie dazu
jedes Restnetzwerk sowie nach jeder Augmentierung den aktuellen Zustand des Flussnetzwerks an. Geben Sie
auÿerdem den Wert des maximalen Flusses an.
Aufgabe 6 (FordFulkerson):
(6 Punkte)
Betrachten Sie das folgende Flussnetzwerk mit Quelle s und Senke t:
5
Datenstrukturen und Algorithmen SS14
Übungsblatt 11 (Abgabe 14.07.2014)
A
2
3
s
7
D
5
B
7
G
1
6
4
E
9
H
1
5
C
t
8
9
3
F
5
I
Berechnen Sie den maximalen Fluss in diesem Netzwerk mithilfe der Ford-Fulkerson Methode. Geben Sie dazu
jedes Restnetzwerk sowie nach jeder Augmentierung den aktuellen Zustand des Flussnetzwerks an. Geben Sie
auÿerdem den Wert des maximalen Flusses an.
6