Link-Ebene Physik Aufgabenbeispiel: Induktivität einer Spule Eine

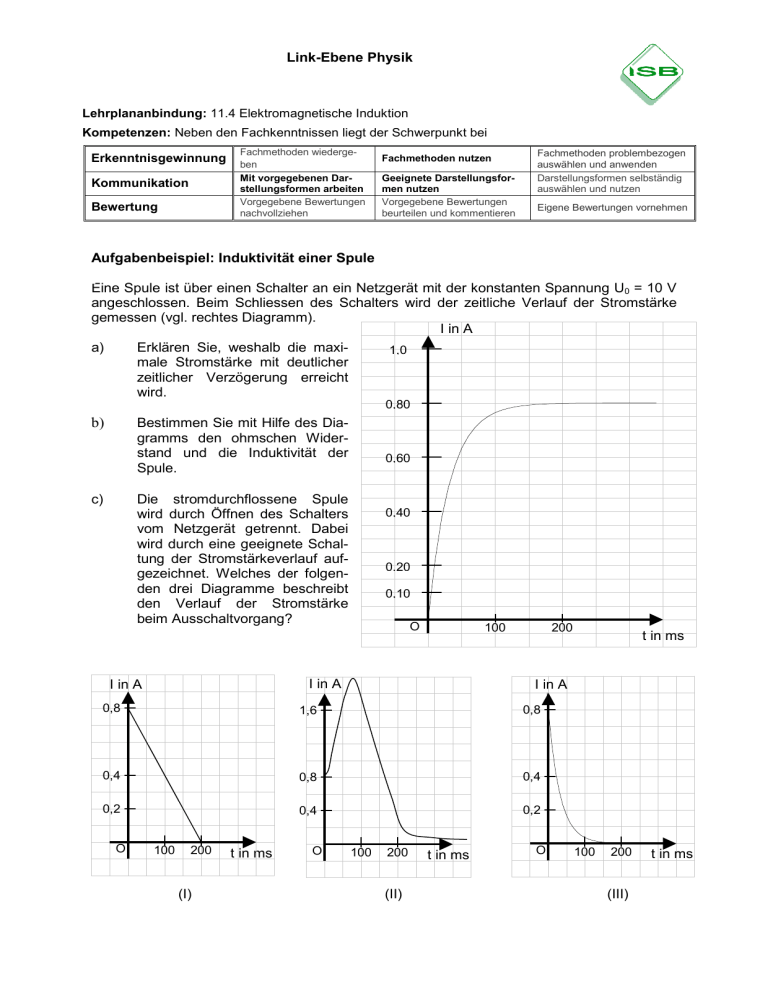
Link-Ebene Physik
Lehrplananbindung: 11.4 Elektromagnetische Induktion
Kompetenzen: Neben den Fachkenntnissen liegt der Schwerpunkt bei
Erkenntnisgewinnung
Kommunikation
Bewertung
Fachmethoden wiedergeben
Mit vorgegebenen Darstellungsformen arbeiten
Vorgegebene Bewertungen
nachvollziehen
Fachmethoden nutzen
Geeignete Darstellungsformen nutzen
Vorgegebene Bewertungen
beurteilen und kommentieren
Fachmethoden problembezogen
auswählen und anwenden
Darstellungsformen selbständig
auswählen und nutzen
Eigene Bewertungen vornehmen
Aufgabenbeispiel: Induktivität einer Spule
Eine Spule ist über einen Schalter an ein Netzgerät mit der konstanten Spannung U0 = 10 V
angeschlossen. Beim Schliessen des Schalters wird der zeitliche Verlauf der Stromstärke
gemessen (vgl. rechtes Diagramm).
I in A
a)
Erklären Sie, weshalb die maxi1,0
male Stromstärke mit deutlicher
zeitlicher Verzögerung erreicht
wird.
0,80
b)
Bestimmen Sie mit Hilfe des Diagramms den ohmschen Widerstand und die Induktivität der
Spule.
c)
0,60
Die stromdurchflossene Spule
wird durch Öffnen des Schalters
vom Netzgerät getrennt. Dabei
wird durch eine geeignete Schaltung der Stromstärkeverlauf aufgezeichnet. Welches der folgenden drei Diagramme beschreibt
den Verlauf der Stromstärke
beim Ausschaltvorgang?
0,40
0,20
0,10
O
100
I in A
I in A
200
I in A
0,8
1,6
0,8
0,4
0,8
0,4
0,2
0,4
0,2
O
100
200
(I)
t in ms
O
t in ms
100
200
(II)
t in ms
O
100
200
(III)
t in ms
Lösungen:
a)
Nach dem Schließen des Schalters beginnt die Stromstärke in der Spule anzusteigen. Dabei nimmt die magnetische Flussdichte und damit auch der magnetische
& ( t ) > 0 ). Nach der lenzschen Regel wird eine GegenFluss durch die Spule zu ( Φ
spannung induziert, welche ihrer Ursache, also dem Anstieg der Stromstärke entge& ( t ) < 0 ).
genwirkt ( U ind ( t ) = − N ⋅ Φ
b)
R=
U0
10 V
=
= 12,5 Ω
Imax 0,80 A
U (t = 0)
10 V
L = &ind
=
= 0,56 H
18 As−1
I(t = 0)
Die Ableitung &I(t = 0) lässt sich aus
dem Diagramm als Tangentensteigung im Ursprung bestimmen.
&I( t = 0) = ∆I = 0,9 A = 18 As−1
∆t 0,050 s
(Streuung der Ergebnisse im Rahmen der Zeichengenauigkeit!)
c)
I in A
1,0
0,8
0,6
∆I = 0,9 A
0,4
Diagramm (III)
0,2
0,1
t in ms
∆t = 50 ms
O
100
200