k kn nn knk n k n ∙ ∙ ∙ + - ∙ ∙ - ∙ =

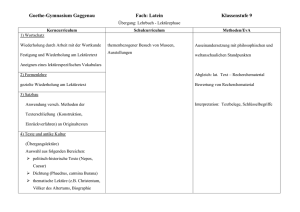
SEMINAR 1
WIEDERHOLUNG - KOMBINATORIK
Auswahl/Ziehung
Mit Wiederholung:
Auswahl/Ziehung von Elementen bei der das gewählte/gezogene Element sofort
wieder der Gesamtmenge zugefügt wird.
Ohne Wiederholung: Auswahl/Ziehung von Elementen bei der das gewählte/gezogene Element nicht
wieder der Gesamtmenge zugefügt wird.
Permutation
Definition (Permutation):
Jede mögliche Anordnung von n Elementen, in der alle Elemente verwendet werden, heißt
Permutation dieser Elemente.
Permutation ohne Wiederholung:
Satz (Permutation ohne Wiederholung):
Von n paarweise verschiedenen Elementen gibt es n! Permutationen (also Anordnungsmöglichkeiten).
Permutation mit Wiederholung:
Satz (Permutation mit Wiederholung):
Gegeben seien n Elemente in r Gruppen, wobei sich die Elemente einer Gruppe nicht unterscheiden,
Elemente verschiedener Gruppen aber verschieden sind. Die Anzahl der Elemente in den Gruppen sei
i1, i2,... , ir (i1 + i2 + ··· + ir = n).
Zu diesen Elementen gibt es
n!
i1! i2 !  ir !
Permutationen (Anordnungsmöglichkeiten).
Beispiel: Wie viele Möglichkeiten gibt es aus den Zahlen 1 bis 4 jeweils 7-stellige Zahlen zu bilden, in denen
2mal die 1, 3mal die 2 und je einmal die 3 bzw. die 4 vorkommen?
Lösung:
→ Permutation mit Wiederholung:
7!
 420
2! 3! 1! 1!
Kombination
Definition (Kombination):
Jede mögliche Anordnung (ohne Berücksichtigung der Reihenfolge) aus je k von n Elementen heißt
Kombination dieser Elemente (Kombination von n Elementen zur k-ten Klasse).
Kombination ohne Wiederholung: K
oder
C
Satz (Kombination ohne Wiederholung):
Aus n verschiedenen Elementen können k Stück (k ≤n) ohne Berücksichtigung der Reihenfolge und
ohne zwischenzeitliches Zurücklegen auf
n
n  (n  1)   (n  k  1)
n!
  

1 2   k
 k  k!  (n  k )!
verschiedene Arten ausgewählt werden.
Kombination mit Wiederholung:
Satz (Kombination mit Wiederholung):
Aus n verschiedenen Elementen werde k-mal hintereinander eines ausgewählt und vor dem nächsten
Zug wieder zurückgelegt. Dann gibt es ohne Berücksichtigung der Reihenfolge insgesamt
verschiedene Auswahlmöglichkeiten.
Beispiel:
Wie viele Möglichkeiten gibt es, 5 (nicht unterscheidbare) Äpfel auf 3 Kinder (K1,K2,K3) zu verteilen? Z.B.:
Erste Lösungsmethode:
Wir können alle Ergebnisse durch Ziffernfolgen kennzeichnen, wobei 0 für einen Apfel und 1
für eine „Trennwand“ zwischen den Kindern steht:
a) 0010100 b) 0001100 c) 1010000
Reformulierung: Wie viele Möglichkeiten gibt es, 5 Nullen und 2 Einsen auf 7 Plätze zu verteilen?
7! / (5!2!) = 21
Zweite Lösungsmethode: → Kombination mit Wiederholung: n = 3, k = 5
Kombination mit Wiederholung: aus der Menge mit 3 Kindern, wählt man 5-mal, mit Wiederholung
bei a) K1,K1,K1,K2,K3,K3, bei b) K1,K1,K1,K3,K3, bei c) K2,K3,K3,K3,K3
Verallgemeinerung:
Wie viele Möglichkeiten gibt es, k (nicht unterscheidbare) Äpfel auf n Kinder zu verteilen?
vgl. obiges Beispiel: k Nullen, n-1 Einsen, auf k+(n-1) Plätze, also

Möglichkeiten.
Variation
Definition (Variation):
Jede mögliche Anordnung (mit Berücksichtigung der Reihenfolge) aus je k von n Elementen heißt
Variation dieser Elemente (Variation von n Elementen zur k-ten Klasse).
Variation ohne Wiederholung:
Satz (Variation ohne Wiederholung):
Aus n verschiedenen Elementen können k Stück (k ≤n) mit Berücksichtigung der Reihenfolge und
ohne Zurücklegen auf
n
n!
   k! 
 n  (n  1) 
(n  k )!
k 
verschiedene Arten ausgewählt werden.
 (n  k  1)
Variation mit Wiederholung:
Satz (Variation mit Wiederholung):
Aus n verschiedenen Elementen werde k-mal hintereinander eines ausgewählt und vor dem nächsten
Zug wieder zur Grundmenge zurückgelegt. Dann gibt es unter Berücksichtigung der Reihenfolge
insgesamt nk verschiedene Auswahlmöglichkeiten.
Beispiel:
Wie viele Möglichkeiten gibt es, aus den Ziffern 1 bis 4 jeweils 6-stellige Zahlen zu bilden, wobei jede Ziffer
beliebig oft vorkommen darf?
Lösung:
→ Variation mit Wiederholung:
= 46 = 4 · 4 · 4 · 4 · 4 · 4 = 4096
Übersicht Ziehung mit/ohne Wiederholung (Zurücklegen):
Ziehung
Mit Wiederholung
(mit Zurücklegen)
Ohne Wiederholung
(ohne Zurücklegen)
Mit Beachtung der
Reihenfolge
nk
n!
(n  k )!
Variation
Ohne Beachtung der
Reihenfolge
 n  k  1


k


n
n!
  
 k  k!  (n  k )!
Kombination