Klassische Theoretische Physik III WS 2014/2015 Blatt 9 Lösungen

Karlsruher Institut für Technologie
Institut für Theorie
der Kondensierten Materie
Klassische Theoretische Physik III
WS 2014/2015
Blatt 9
Lösungen
Prof. Dr. A. Shnirman
Dr. B. Narozhny
1. Coulomb-Eichung:
(3+2+2+3=10 Punkte)
In Coulomb-Eichung gilt
~ ·A
~ = 0.
∇
(a) Zeigen Sie, dass die Stromdichte ~j als Summe eines “parallelen” Anteils ~jk und
eines “senkrechten” Anteils ~j⊥ geschrieben werden kann, wobei die zwei Anteile die
folgenen Form haben:
Z
~
~ 0
~ ~r d3 r0 ∇~r 0 · j(~r ) ,
~jk ∝ ∇
|~r − ~r 0 |
Z
~ 0
~ ~r × ∇
~ ~r × d3 r0 j(~r ) .
~j⊥ ∝ ∇
|~r − ~r 0 |
Es gibt ein mathematische Theorem (das Helmholz-Theorem), das besagt, dass es
möglich ist, jedes Vektorfeld ~a, das im Unendlichen abklingt ~a(~r → ∞) → 0, als
Superposition eines rotationsfreien (wirbelfreien) Feldes und eines divergenzfreien
(quellenfreien) Feldes darzustellen.
Der Beweis:
Z
Z
1
1
3 0
0
0
~ ~2r
d3 r0~a(~r 0 )∇
.
~a(~r) = d r ~a(~r )δ(~r − ~r ) = −
4π
|~r − ~r 0 |
Benutzen wir die Identität
~ 2~x = ∇
~ ∇
~ · ~x − ∇
~ × ∇
~ × ~x .
∇
Wir finden
Z
Z
1 ~
a(~r 0 )
a(~r 0 )
3 0 ~
3 0 ~
~
~
~
~a(~r) = −
∇~r ∇~r · d r
− ∇~r × ∇~r × d r
4π
|~r − ~r 0 |
|~r − ~r 0 |
Z
Z
1 ~
1
1
3 0
0
3
0
0
~ ~r
~ ~r × d r ~a(~r ) × ∇
~ ~r
=−
∇~r d r ~a(~r ) · ∇
+∇
4π
|~r − ~r 0 |
|~r − ~r 0 |
Z
Z
1 ~
1
1
3 0
0
3 0
0
~
~
~
=
∇~r d r ~a(~r ) · ∇~r 0
+ ∇~r × d r ~a(~r ) × ∇~r 0
.
4π
|~r − ~r 0 |
|~r − ~r 0 |
Jetzt benutzen wir die Identitäten
~ = −ψ ∇
~ · ~x + ∇
~ · (ψ~x) ,
~x · ∇ψ
~ = ψ∇
~ × ~x − ∇
~ × (ψ~x) .
~x × ∇ψ
Wir finden
"
Z
1
~
−∇~r d3 r0
~a(~r) =
4π
~ ~r ×
+∇
0
~ ~r 0 · ~a(~r 0 )
∇
~ ~r 0 · ~a(~r )
−
∇
|~r − ~r 0 |
|~r − ~r 0 |
Z
3 0
dr
!
0
~ ~r 0 × ~a(~r 0 )
∇
~ ~r 0 × ~a(~r )
−
∇
|~r − ~r 0 |
|~r − ~r 0 |
!#
.
Benutzen wir jetzt den gaußschen integralsatz und die Tatsache, dass unseres Vektorfeld im Unendlichen verschwindet. Wir finden letztendlich
"
#
Z
Z
~ ~r 0 × ~a(~r 0 )
~ ~r 0 · ~a(~r 0 )
1
∇
∇
~ ~r d3 r0
~ ~r × d3 r0
~a(~r) =
−∇
+∇
.
4π
|~r − ~r 0 |
|~r − ~r 0 |
Es ist also möglich das Vektorfeld ~j durch Superposition zweier unterschiedlicher
Potentiale auszudrücken
~ × ~jk = 0,
∇
~j = ~jk + ~j⊥ ,
~ · ~j⊥ = 0.
∇
Z
~
~ 0
1
~ ~r d3 r0 ∇~r 0 · j(~r ) ,
~jk = − ∇
4π
|~r − ~r 0 |
Z
Z
~
~ 0
~ 0
~ ~r × ∇
~ ~r × d3 r0 j(~r ) = 1 ∇
~ ~r × d3 r0 ∇~r 0 × j(~r ) .
~j⊥ = 1 ∇
4π
|~r − ~r 0 |
4π
|~r − ~r 0 |
Finden Sie die Koeffizienten in die SI und die Gausschen Einheitssystemen.
Das Helmholz-Theorem hat mit der Einheitssystemen gar nichts zu tun. Deswegen
sind die Koeffizienten in die SI und die Gausschen Einheitssystemen gleich.
(b) Berechnen Sie die fouriertransformierte parallele und senkrechte Stromdichte ~jk (~k)
und ~j⊥ (~k). Die Fouriertransformation ist dabei definiert als
Z
d3 k ~ ~ i~k·~r
~j(~r) =
j(k)e .
(2π)3
Die Umkehrtransformation lautet
~j(~k) =
Z
~
d3 r~j(~r)e−ik·~r .
Es gilt die Orthogonalitätsbeziehung
Z
~
d3 re−ik·~r = (2π)3 δ(~k),
und
Z
d3 k i~k·~r
e = δ(~r).
(2π)3
Wir betrachten zunächst die parallele Stromdichte:
Z
~jk (~r) =
R
Z
~ 0 · d3 k3 ~j(~k)ei~k·~r 0
∇
d3 k ~ ~ i~k·~r
1 ~
(2π)
= − ∇ d3 r 0
3 jk (k)e
4π
|~r − ~r 0 |
(2π)
Z
Z 3 ~ ~~
1 ~
d k ik · j(k) i~k·~r 0
3 0
=− ∇ d r
e
4π
(2π)3 |~r − ~r 0 |
und translatieren ~r 0 um ~r. Da wir nur translatieren, verändert sich das Integrationsmaß nicht und da wir über den ganzen Raum integrieren, ändern sich die
Integrationsgrenzen nicht:
Z
Z 3 ~ ~~
~
r1 ≡~
r 0 −~
r
d k ik · j(k) i~k·~r1 i~k·~r
1
z}|{
3
~ d r1
~jk (~r) = − ∇
e
e
4π
(2π)3 |~r1 |
!
Z 3
Z
~k · ~j(~k) ~
dk
1
i
~
=
−
eik·~r1 eik·~r .
d3 r1 (i~k)
3
(2π)
4π
|~r1 |
Es folgt,
Z
i~k·~
r1
~k Z
~k · ~j(~k) ~
i
i
1
3
i
k·~
r
3 e
1
~
~
~
~jk (~k) = −
~
d r1
e
k k · j(k)
d r1
.
=
4π
|~r1 |
4π
|~r1 |
Kümmern wir uns nun um die Fouriertransformation von 1/ |~r|:
Z
~
eik·~r
=
dr
|~r|
3
Z2π Zπ
Z∞
Z1 Z∞
ikr cos θ
dφ dθ sin θ dr re
= 2π dt dr reikrt
0
0
0
−1
0
Z∞
Z∞
sin kr
1 ikr
−ikr
.
= 4π dr
= −2πi dr e − e
k
k
0
0
Hierbei wurde die z-Achse in ~k-Richtung gelegt und zu Kugelkoordinaten gewechselt. Wir führen den konvergenzerzeugenden Faktor > 0 ein (am Ende schicken
wir → 0) und erhalten
Z
~
eik·~r
4π
dr
= lim
→0
r
k
3
Z∞
Z∞
4π
−r
dre sin kr = lim Im dre(ik−)r
→0 k
0
0
∞
4π
e(ik−)r
= lim Im
→0 k
ik − 0
= lim
→0
= lim
→0
∞
4π
Im (ik + ) (cos kr + i sin kr) e−r 0
2
+ )
k
(k 2
k
(k 2
4π
4π
Im (ik + ) = 2 .
2
+ )
k
Somit ergibt sich
~k ~k · ~j(~k)
~jk (~k) = 1 ~k ~k · ~j(~k) 4π =
.
4π
k2
k2
Da die Fouriertransformation linear ist, erhalten wir die Komponente j⊥α (~k) einfach
aus
k α k β j β (~k)
kαkβ
α ~
α ~
α ~
α ~
αβ
j⊥ (k) = j (k) − jk (k) = j (k) −
j β (~k).
= δ − 2
k2
k
Warum werden ~jk und ~j⊥ parallele bzw. senkrechte Stromdichte genannt?
Aus unsere Ergebnisse wird ersichtlich, dass ~jk (~k) in ~k-Richtung zeigt. Insgesamt
gilt also
~jk (~k)k~k,
~j⊥ (~k)⊥~k.
Die Bezeichnungen senkrechter (transversaler) Anteil für ~j⊥ und paralleler (longitudinaler) Anteil für ~jk beziehen sich also auf die Richtung von ~k.
(c) Finden Sie
~ · ~jk ,
∇
~ × ~jk ,
∇
~ · ~j⊥ ,
∇
~ × ~j⊥ .
∇
Wir betrachten zunächst die Divergenz einer Rotation und die Rotation eines Gradienten:
~
~
∇ · ∇ × ~a = ∂xi εijk ∂xj ak = 0,
h
i
~
~
∇× ∇·b
= εijk ∂xi ∂xj b = 0.
k
Beide Ausdrücke verschwinden, da die Kontraktion des antisymmetrischen Tensors
εijk mit den symmetrischen Tensoren ∂i ∂j ak , bzw. ∂i ∂j b verschwindet. Hierbei nehmen wir an, dass ak und b zweimal stetig differenzierbar sind. Es folgt
~ × ~jk = ∇
~ · ~j⊥ = 0.
∇
Betrachten wir nun
~ · ~jk = − 1 ∇
~2
∇
4π
Z
d3 r0
~ 0 · ~j (~r 0 )
∇
.
|~r − ~r 0 |
Benutzen wir jetzt die Identiät
~2
∇
und finden
~ · ~jk =
∇
Z
1
= −4πδ(~r − ~r 0 ) ,
|~r − ~r 0 |
~ 0 · ~j (~r 0 ) δ(~r − ~r 0 ) = ∇
~ · ~j.
d3 r 0 ∇
Betrachten wir nun die verbleibende Rotation
~ ×∇
~ ×∇
~ ×
~ × ~j⊥ = 1 ∇
∇
4π
Z
d3 r 0
~j (~r 0 )
.
|~r − ~r 0 |
Mit der Identität
∇ × (∇ × ~a) = ∇(∇ · ~a) − ∇2~a,
erhalten wir
h i
~ ×∇
~ ×∇
~ × ~a = ∇
~ × ∇
~ ∇
~ · ~a − ∇
~ 2~a = −∇
~ × ∇
~ 2~a .
∇
Letztendlich
~ × ~j⊥ = ∇
~ × ~j.
∇
Alternativ hätte man auch einfach die Rotation und Divergenz des Stromes betrachten können:
~ × ~j⊥ = ∇
~ × ~j⊥ ,
~ × ~j = ∇
~ × ~jk +∇
∇
| {z }
0
~ · ~j = ∇
~ · ~jk + ∇
~ · ~j = ∇
~ · ~jk .
∇
| {z ⊥}
0
(d) Beweisen Sie die folgende Identitäten (in Gaussschen Einheitssystem):
1~ ∂
4π
∇ ϕ = ~jk ,
c ∂t
c
~−
∇2 A
1 ∂2 ~
4π
A = − ~j⊥ .
2
2
c ∂t
c
Wir betrachten die beiden inhomogenen Maxwell Gleichungen im Vakuum
~ ·E
~ = 4πρ,
∇
~
~ ×B
~ = 4π ~j + 1 ∂ E .
∇
c
c ∂t
Wenn wir die Felder durch die elektromagnetischen Potentiale
~
~ = −∇ϕ
~ − 1 ∂A ,
E
c ∂t
~ =∇
~ × A,
~
B
ausdrücken, erhalten wir
~ ·A
~ = 4πρ,
~ ·E
~ = −∆ϕ − 1 ∂ ∇
∇
c ∂t
und
2~
~ ·A
~ − ∆A = 4π ~j − 1 ∂ A − 1 ∇
~ ×B
~ =∇
~ ×∇
~ ×A=∇
~ ∇
~ ∂ϕ .
∇
2
2
c
c ∂t
c ∂t
~ ·A
~ = 0 vereinfachen sich die Gleichungen zu
Durch die Coulomb-Eichung ∇
∆ϕ = −4πρ,
~ = 1∇
~ ∂ϕ − 4π ~j,
A
c ∂t
c
mit = ∆ − (1/c2 )∂ 2 /∂t2 .
Die erste Gleichung erkennen wir als Poisson-Gleichung mit der Lösung
Z
ρ(~r 0 , t)
ϕ(~r, t) = d3 r0
.
|~r − ~r 0 |
Mit der Kontinuitätsgleichung
∂ρ ~ ~
+ ∇ · j = 0,
∂t
erhalten wir
1 ~ ∂ϕ
1~
=− ∇
∇
c ∂t
c
und auch
~=
A
Z
d3 r 0
~ 0 · ~j(~r 0 , t)
4π
∇
= ~jk ,
0
|~r − ~r |
c
4π ~
4π ~
4π
jk −
jk + ~j⊥ = − ~j⊥ .
c
c
c
Wie sehen sich diese Identitäten in SI-System aus?
~ ∂ ϕ = 1 ~jk ,
∇
∂t
0
~−
∇2 A
1 ∂2 ~
A = −µ0~j⊥ .
c2 ∂t2
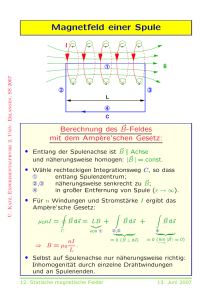
2. Drehimpuls einer langen Spule:
(10 Punkte)
Stellen Sie sich eine sehr lange Spule mit Radius R vor, die n Windungen pro Längeneinheit besitzt und den Strom I führt. Koaxial zur Spule liegen zwei lange zylinderförmige
Schalen der Länge L - die eine, mit Radius a innerhalb der Spule gelegen, trägt diegleichförmig auf die Oberfläche verteilte Ladung Q, die andere, mit Radius b L außerhalb der Spule gelegen, trägt die Ladung −Q. Wird der Strom in der Spule allmählich
zu Null reduziert, beginnen die Zylinder zu rotieren.
Berechnen Sie den Drehimpuls, der am Anfang in den Felder gespeichert war, und
vergleichen ihn mit dem mechanischen Drehimpuls der rotierenden Zylindern.
Wir benutzen die zylindrischen Koordinaten (ρ, ϕ, z).
Das elektrische Feld inzwischen der Schalen:
~ =
E
Q ~eρ
,
2π0 L ρ
a < ρ < b.
Mit dem Strom:
Das magnetische Feld innerhalb der Spule:
~ = µ0 nI~ez ,
B
ρ < R.
Die Impulsdichte des elektromagnetischen Feldes
~ = 0 µ0 S
~ = − µ0 nIQ ~eϕ ,
P
2πlρ
a < ρ < R.
Deswegen, finden wir die Drehimpulsdichte des Feldes als
~` = ~r × P
~ = − µ0 nIQ ~ez .
2πl
Die Dichte ist konstant. Der Drehimpuls ist denn
~ = ~rV,
L
~ = − 1 µ0 nIQ(R2 − a2 )~ez .
L
2
V = π(R2 − a2 )l,
Als man den Strom reduziert:
Finden wir erst das induzierten elektrischen Feld (nach dem Faraday Gesetz)
(
2
dI
1
~ = − µ0 n ~eϕ R /ρ, ρ > R,
E
2
dt
ρ,
ρ < R.
Das Drehmoment auf die Außenschale ist
~ b = −Q~r × E
~ = 1 µ0 nQR2 dI ~ez .
N
2
dt
Die Außenschale “picks up” den Drehimpuls
~ b = 1 µ0 nQR2~ez
L
2
Z0
dt
dI
1
= − µ0 nIQR2~ez .
dt
2
I
Änlicherweise für die Innenschale
~ a = − 1 µ0 nQa2 dI ~ez ,
N
2
dt
~ a = 1 µ0 nIQa2~ez .
L
2
Die Schalen rotieren gegenläufig!
Das Gesamtdrehimpuls ist erhalten
~ =L
~a + L
~ b.
L
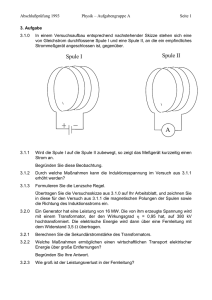
3. Poynting-Vektor:
(5+5=10 Punkte)
Eine sehr lange Spule mit Radius a und n Windungen pro Längeneinheit trägt einen
Strom I. Koaxial mit der Spule befindet sich bei b a ein kreisförmiger Drahtring
mit Widertand R. Verringert man den Strom in der Spule (allmählich), dann wird ein
Strom J im Ring induziert.
(a) Bestimmen Sie J in Abhängigkeit von dI/dt.
ξ=−
dΦ
,
dt
J=
Φ = πa2 B,
B = µ0 nI.
ξ
1
dI
= − µ0 πa2 n .
R
R
dt
(b) Die auf den Ring übertragene Leistung muss aus der Spule stammen. Bestätigen
Sie dies, indem Sie den Poynting-Vektor direct außerhalb der Spule berechnen. Integrieren Sie über die gesamte Fläche der Spule und überprüfen Sie, dass Sie die
richtige Gesamtleistung erhalten.
Das induzierte elektrische Feld finden wir vom Faraday Gesetz:
I
~ · d~l = − dΦ .
E
dt
E(2πa) = −µ0 πa2 n
dI
dt
⇒
~ = − 1 µ0 an dI ~eϕ .
E
2
dt
Das Magnetfeld des Drahtrings ist
b2
~ = 1 µ0 J
~ez .
B
2
(b2 + z 2 )3/2
Das findet man ähnlich zu Blatt 7, Aufgabe (a1):
~ r ) = µ0 J
B(~
4π
Z
Z
µ0 J
µ0 J cos θ
µ0 Jb2
d~l0 × ~r
cos θdl0
=
~
e
=
2πb~
e
=
~ez .
z
z
r3
4π
r2
4π r2
2 (b2 + z 2 )3/2
Der Poynting-Vektor ist
#
"
2
~ ×B
~
E
µ0 nJab2 dI
1
1
dI
1
b
~=
S
~
e
×
~
e
=
−
=
− µ0 an
µ0 J
~eρ .
ϕ
z
µ0
µ0
2
dt
2
(b2 + z 2 )3/2
4 (b2 + z 2 )3/2 dt
Die Leistung ist
Z
P =
Z∞
~ · dA
~=
S
π
dI
dzS2πa = − µ0 nJ a2 b2
2
dt
−∞
2 dI
= − πµ0 na
= J 2 R.
dt
Z∞
−∞
J
dz
(b2 + z 2 )3/2