ps.gz

Extrablatt (nicht mit einbinden!)
D fur = [IFPX;x '(X; x)]t
D'0
6
6
j
y := z
G
6y := z
y := x
E x? - H
I
i
`
`
`
`
`
j `
`
`
`
`
`
`
`
j `
`
`
`
`
`
`
`
-D
6
-A
x?
F
s0 : jxj = 1
`
jxj > 1
jxj jyj
j
Start
j
@@
@@ z?
xz := tt - C 6
j
j
z?
@
j
x := y
j
@
@@R ?
B
j `
`
`
`
jxj > jzj
?
`
`
`
`
`
:(jxj jzj + 1 jyj)
`
`
`
`
`
D'
s : jxj jzj + 1
`
i
`
`
e : jxj jzj
`
i
In D':
-
j
j
X r1!
X r2!
j
j
-
j
j
j
j
..
.
..
.
-
j
In D' :
In D'0 :
X rk!
j
-
j
j
-
x := r1
@
@@
- x := r-
-@RExit
..
.
- x := r-k j
j
j
2
j
j
j
j
Albert{Ludwigs{Universitat Freiburg
Freiburg im Breisgau
Remisfreie Spiele, Fixpunktlogiken und
Normalformen
Max Kubierschky
email: [email protected]
vorgelegt als Diplomarbeit
bei Herrn Professor Dr. Jorg Flum
im Dezember 1995
Inhaltsverzeichnis
0 Einleitung
0.1
0.2
0.3
0.4
Was bisher geschah : : : : : : : : : :
Was Sie in dieser Abhandlung lesen :
Aufbau : : : : : : : : : : : : : : : :
Sprache : : : : : : : : : : : : : : : :
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
Strukturen : : : : : : : : : : : : : : : : : :
Signaturen : : : : : : : : : : : : : : : : : : :
Belegungen und Interpretationen : : : : : :
Logiken : : : : : : : : : : : : : : : : : : : :
Tupel : : : : : : : : : : : : : : : : : : : : :
Die \Variable" d : : : : : : : : : : : : : : :
Abhangigkeit von Variablen, Einsetzungen :
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
1 Allgemeine Geschaftsbedingungen
1.1
1.2
1.3
1.4
1.5
1.6
1.7
3
3
3
4
4
7
7
7
7
8
8
8
8
2 Fixpunktlogiken
3 Reduktionen und vollstandige Probleme
4 Spiele
11
13
15
5 Diagramme
19
6 Zwischenspiel
7 Beweis des Hauptsatzes
8 Normalformen fur IFP
8.1 Vollstandigkeit von GAME : : : : : : : : : : : : : : : : : : : : : : :
23
29
39
9 Negative PFP-Fragmente
43
4.1 Denitionen : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 15
4.2 Remisfreie Spiele : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 16
4.3 Der Hauptsatz : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 17
5.1 Denition : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 19
5.2 Diagramme und quantorenfreie U bersetzungen : : : : : : : : : : : : 21
5.3 Subdiagramme : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 22
39
8.2 Skolemsche Normalform, IFP=LFP : : : : : : : : : : : : : : : : : : : 39
8.3 Beschrankte Skolemsche Normalform : : : : : : : : : : : : : : : : : : 40
9.1
9.2
9.3
9.4
Denition : : :
Klassizierung
negPFP : : : :
PFPNF(0,1) : :
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
1
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
43
43
44
45
2
9.5 Happy End : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 46
A Literatur
47
Kapitel 0
Einleitung
0.1 Was bisher geschah
Fixpunktlogiken sind Erweiterungen der Logik 1.Stufe durch einen Operator fur induktive Denitionen. Sie sind eng mit Komplexitatsklassen verwandt. So sind zum
Beispiel die endlichen Klassen geordneter Strukturen, die in der Fixpunktlogik IFP
denierbar sind, genau diejenigen, die in PTIME berechenbar sind [Var82,Imm82].
Auch andere Begrie der Komplexitatstheorie lassen sich in die Logik ubertragen,
insbesondere die der Reduktion und des vollstandigen Problems.
Das vollstandige Problem, das uns hier interessiert, ist das Geographiespiel1. Geographiespiele werden auf Strukturen mit einer Kantenrelation gespielt. Die Spielerinnen ziehen von einer Startposition aus einen Spielstein abwechselnd entlang
einer Kante. Wer nicht ziehen kann, hat verloren. Das Problem, zu entscheiden, wer
das Geographiespiel auf einer gegebenen Struktur mit einer gegebenen Startstellung gewinnt, ist vollstandig fur PTIME bezuglich LOGSPACE-Reduktion2 [JS76]3
Die entsprechende Aussage in der Logik ist, da das Geographiespiel auf geordneten Strukturen vollstandig fur IFP bezuglich DTC4 -Reduktion ist5 . Sie lat sich
in doppelter Weise verscharfen: Das Geographiespiel ist vollstandig fur IFP, sogar bezuglich quantorenfreier Reduktion auf allen endlichen Strukturen, auch ohne
Ordnungsrelation [Dah87]6 .
0.2 Was Sie in dieser Abhandlung lesen
Ausgangspunkt der Arbeit war die Frage, wie ausdrucksstark Fixpunktoperatoren
der Form [FPX x 9z2= X'(x; z)] mit quantorenfreiem ' sind. Diese stehen in engem
Zusammenhang mit dem Geographiespiel.
Betrachtet man '(x; z) als Denition einer Kantenrelation, so charakterisiert dieser
Operator die Gewinnstellungen im zugehorigen Geographiespiel, wenn der Fixpunkt
existiert.
1 Dieser Name kommt von einem Spiel, bei dem abwechselnd z.B. eine Stadt genannt wird, die
mit dem Buchstaben anfangen mu, mit dem die vorige aufgehort hat.
2 In obiger Variante. Meistens verbietet man beim Geographiespiel Wiederholungen, das heit
der Spielstein darf nicht ein zweites mal auf ein schon benutztes Feld gezogen werden. Mit diesem
Verbot ist das Geographiespiel vollstandig fur PSPACE (ndet man in [Rei90]).
3 In [JS76] wird dies f
ur eine Klasse GAME gezeigt, die etwas aufwendiger deniert ist, als das
Geographiespiel. Das Ergebnis lat sich aber leicht auf das Geographiespiel ubertragen.
4 DTC ist die Erweiterung der Logik erster Stufe durch einen Operator f
ur die transitive Hulle
denierbarer deterministischer (d.h. rechtseindeutiger) Relationen.
5 Diese Entsprechung ndet man als U
 bung in [EF95].
6 [Dah87] bezieht sich ebenfalls auf die Klasse GAME aus [JS76].
3
4
Konnte man sich darauf verlassen, da er existiert, so ware es dank der Vollstandigkeit des Geographiespiels leicht zu beweisen, da solche Operatoren so ausdrucksstark sind wie IFP. Leider ist dies nicht der Fall. Er existiert nur, wenn das zugehorige Spiel remisfrei ist, d.h. wenn es keine Stellungen gibt, in denen keine der beiden
Parteien eine Gewinnstrategie hat. Es stellt sich also die Frage, ob man mit solchen
Formeln '(x; z) auskommt, die remisfreie Spiele denieren. Anders formuliert: Sind
die remisfreien Geographiespiele vollstandig fur IFP?
Die Theorie der remisfreien Spiele hat sich als fruchtbar erwiesen. Unser Programm
ist folgendes: Zunachst wird ein \Hauptsatz" bewiesen, der in etwa sagt, da die remisfreien Geographiespiele tatsachlich vollstandig fur IFP bezuglich quantorenfreier
Reduktion sind. Dieser wird direkt bewiesen, also ohne Ruckgri auf Normalformen
oder sonstige Satze uber Fixpunktlogiken. Aus dem Hauptsatz folgt recht einfach
eine schone Normalform fur IFP, die gleichzeitig IFP=LFP beweist. Zum Schlu beantworten wir, sozusagen als Anwendung, die Ausgangsfrage in einer allgemeineren
Form.
0.3 Aufbau
Hier die Kapitel im Einzelnen:
Das erste Kapitel dient dazu, die Formalitaten zu regeln. Es werden Begriichkeiten
geklart und Grundannahmen benannt, die in der restlichen Arbeit implizit bleiben
oder verschwiegen werden. Einige Notationen und Konventionen werden festgelegt
und einige Schlampigkeiten legalisiert.
Die Kapitel Fixpunktlogiken sowie Reduktionen und vollstandige Probleme
sind Auistungen von Denitionen und einfachen Sachverhalten, diese Gegenstande
betreend. Sie sind weniger als Erklarung gedacht, sondern eher als Referenz. Alle
Satze sind dort ohne Beweis wiedergegeben, weil sie erstens leicht sind und zweitens
allgemein bekannt. Etwas ausfuhrlicher behandelt ndet man diesen Sto in [EF95].
Im Kapitel Spiele wird deniert, was wir unter Spielen und Gewinnstrategien verstehen. Es werden remisfreie Spiele eingefuhrt und der Hauptsatz formuliert.
Das Kapitel Diagramme stellt das zentrale Hilfsmittel zum Beweis des Hauptsatzes vor, namlich Diagramme. Sie werden uns das Lesen von Formeln erschreckender
Lange ersparen.
Im Kapitel Zwischenspiel wird ein Beweis fur den Hauptsatz skizziert, der aber
voraussetzt, da bereits bewiesen ist, da das Geographiespiel hart fur IFP ist. Diese Erkenntnis gewinnt man normalerweise aus einer Normalform [Dah87], deshalb
taugt er nichts fur das oben beschriebene Programm. Er wird trotzdem wiedergegeben, weil er anschaulich ist und Konzepte verstandlich macht, die im weniger
anschaulichen Beweis des Hauptsatzes verwendet werden.
Im Kapitel Normalformen fur IFP wird die Ernte eingefahren, diverse Normalformsatze und IFP=LFP werden bewiesen.
Im Kapitel Negative PFP-Fragmente werden die Fragmente von PFP, die von
Fixpunktoperatoren der Form
[FPX x '0 _ 9y1 2 X : : : 9yl 2 X 9z1 2= X : : : 9zm 2= X ' ]t
fur festgehaltene Werte von l und m erzeugt werden, klassiziert und damit die im
vorigen Abschnitt erwahnte Ausgangsfrage gelost.
0.4 Sprache
Ich verwende das geschlechtsneutrale Femininum: Mit \Spielerin" ist nicht
eine spielende Person bekannntermaen weiblichen sondern eine solche unbekannten Geschlechts gemeint. Ebenso fur \Leserin" etc.
5
Da ich kein Freund von Passivkonstruktionen bin und zu bescheiden, um zu
haug das Wort \ich" zu schreiben, habe ich mich nach einigem Hadern fur
das krankenschwesterliche \wir" entschieden. \Wir" meint hier mich selbst
und die Leserin.
6
Kapitel 1
Allgemeine
Geschaftsbedingungen
1.1 Strukturen
Wir betrachten nur endliche Strukturen
Wir betrachten nur Strukturen mit mindestens zwei Elementen
Die erste Einschrankung ist hier wesentlich, die zweite dient nur der Bequemlichkeit.
Der Fall der einelementigen Strukturen ist leicht zu behandeln, uninteressant und
fuhrt zu weniger schonen Normalformen.
1.2 Signaturen
Eigentlich sollten wir Logiken und verwandte Dinge in Abhangigkeit von einer Signatur denieren. Da dies lastig ist, sei hiermit ein fur alle mal gewahlt, und
alle Denitionen sind abhangig von , ohne da dies erwahnt wird. Wo nicht anders
vermerkt, sind Strukturen -Strukturen, Interpretationen -Interpretationen etc.
1.3 Belegungen und Interpretationen
Fur eine Struktur A teilt eine A-Belegung jeder Variable (1. und 2. Stufe) einen
geeigneten Wert in A zu. Eine Interpretation ist ein Paar (A; ). Wo immer es Sinn
macht, werden wir in Denitionen und Satzen mit Interpretationen arbeiten statt
mit Strukturen. Dies vereinfacht die Induktion uber Formeln und den Umgang mit
freien Parametern.
Substitutionen in Belegungen schreiben wir wie folgt: Mit [ xa ] meinen wir die Belegung, die der Variable x den Wert a zuordnet und sich ansonsten so verhalt wie
. Fur A~ = (A; ) sei A~[ xa ] := (A; [ xa ]) und A~(t) := (t). Das Entsprechende gilt
fur 2.Stufe Variablen.
Fur die Bezeichnungen fuhren wir folgende Konvention ein: Auch wenn es nicht
dazu gesagt wird, meint das Symbol A~ stets eine Interpretation (A; ), wobei A
eine Struktur mit Trager A ist.
7
8
1.4 Logiken
Eine Logik L ist fur uns eine Menge F von Formeln zusammen mit einer Modellrelation j= zwischen Interpretationen und Formeln aus F . Fur eine Formel ' ist
Mod(') := fA~ j A~ j= 'g die Modellklasse von '. Zwei Formeln ' und sind aquivalent (wir schreiben: ' =jj= ), wenn ihre Modellklassen gleich sind. Vergleiche
zwischen Logiken (z.B. LFP IFP, LFP = IFP) sind immer als Vergleiche zwichen den Mengen von Modellklassen, die durch die jeweilige Logik denierbar sind,
gemeint.
Eine Sublogik K von L nennen wir Normalform von L, wenn in diesem Sinne K=L
gilt (d.h. fur alle 2 L existiert ein 0 2 K mit =jj= 0 ). Der Name Normalform
macht naturlich nur Sinn, wenn sich die Formeln von K ahnlich sehen.
Wenn wir eine Logik L denieren, ist im Sinne von 1.2 diese Denition abhangig
von der Signatur . Mit L[] meinen wir die entsprechende Logik fur die Signatur
, wenn wir nur L schreiben, meinen wir implizit L[ ].
FO ist die Logik der 1.Stufe, QF sind die quantorenfreien Formeln. In beiden Fallen
erlauben wir freie 2.Stufe Variablen.
Wenn wir eine Denition oder eine Aussage fur eine Formel ' tatigen, ohne dazuzusagen, welcher Logik diese Formel angehoren soll, so ist eine beliebige Logik
gemeint und nur von Belang, da Mod(') deniert ist.
1.5 Tupel
Tupel (von Objekten wie Variablen, Termen oder Elementen einer Struktur) schreiben wir in der Form o0 o1 : : : on 1 (d.h. ohne Klammern
und Kommas) und kurzen
nm
p fur o0 : : : on 1 p0 : : : pm 1 . Wir
o
Schreibweisen
wie
sie durch on ab. Dies erlaubt
schreiben auch o statt on, wenn die Lange n des Tupels aus dem Kontext hervorgeht
oder nicht von Belang ist. Wir schrecken nicht davor zuruck, Tupel nochmals zu
indizieren. onk bedeutet dann ok0 : : : okn 1 .
1.6 Die \Variable" d
In manchen Situationen benotigen wir Tupel aus lauter gleichen Termen, wobei
egal ist, was fur einen Term wir wahlen. Wir verwenden dann stets d~. d sei eine
beliebige Variable, d~ := dd : : : d (die Lange des Tupels entnimmt man jeweils aus
dem Kontext). Auf diese Weise werden Formeln: entstehen, in denen d frei ist, die
aber nicht von d abhangen (triviales Beispiel: d = d ). Um Verwirrung zu vermeiden,
fat man d am besten als Konstante auf. Dies wollen wir aber oziell nicht tun, da
die Forderung, da eine solche Konstante verfugbar ist, eine unnotige Einschrankung
an die Signatur ware.
1.7 Abhangigkeit von Variablen, Einsetzungen
Die Schreibweise '(x) bedeutet weder, da die Variablen x alle frei in ' vorkommen,
noch, da ' keine anderen freien Variablen hat.
Sie dient zweierlei Zwecken. Erstens bietet sie eine einfache Moglichkeit, Substitutionen zu notieren: Fur ' = '(x) ist '(y) die Formel, die entsteht, wenn man in '
alle xi durch yi substituiert. In Modellbeziehungen erlauben wir uns auch, Elemente
von Strukturen einzusetzen. A~ j= '(a) ist als Abkurzung fur A~[ xa ] j= ' zu lesen.
Zweitens verwenden wir sie, um gewisse Variablen als \spezielle" Variablen auszuzeichnen, wie z.B. in der folgenden Denition:
9
Denition 1 ('A~(x;n yn)) Fur eine Formel ' = '(x;n yn) und eine Interpretation A~
ist
n n
n n
n n
y) := f(a;
'A~(x;
b) 2 An An j A~ j= '(a; b)g
n n
y) hangt naturlich nicht nur von der Formel ' und von A~ ab, sondern auch
'A~(x;
n
n n
n
von der Wahl der Variablen x und y. '(x; y) ist also je nach Kontext entweder
als Formel oder als ein Tripel aus
einer Formel und zwei Tupeln von Variablen
n n
y
aufzufassen. Wenn wir ' := '(x; ) schreiben, bedeutet dies, da ' ab sofort dieses
Tripel vertritt (in Kontexten, in denen ein solches gefragt ist).
Alles in diesem Abschnitt Gesagte gilt naturlich entsprechend fur 2.Stufe-Variablen.
10
Kapitel 2
Fixpunktlogiken
Denition 2 (Fixpunkt, F 1(R)) Sei eine Menge A und eine Abbildung
F : Pot(A) ! Pot(A) gegeben.
(i) S An heit ein Fixpunkt von F , wenn F (S ) = S .
(ii) Falls fur ein R An die Folge (F k (R))k2IN
(d.h. die Folge R; F (R); F (F (R)); : : :) bei einem m 2 IN stationar wird (also
F m (R) Fixpunkt ist), sagen wir F 1 (R) existiert und setzen F 1 (R) := F m (R)
(iii) F 1 := F 1 (;) heit der Fixpunkt von F .
Denition 3 (induktiv, monoton, antimonoton)
F : Pot(An ) ! Pot(An ) heit:
induktiv
:, F k (;) F k+1 (;)
fur alle k 2 IN .
monoton
:, R S ) F (R) F (S ) fur alle R; S An .
antimonoton :, R S ) F (R) F (S ) fur alle R; S An .
Satz 4 F monoton ) F induktiv 2
Satz 5 Sei F : Pot(An ) ! Pot(An ) monoton. Dann ist
(i) (F k (;))k2IN eine aufsteigende Folge. F 1(;) existiert und ist der Durchschnitt aller Fixpunkte von F .
(ii) (F k (An ))k2IN eine absteigende Folge. F 1(An ) existiert und ist die Vereinigung aller Fixpunkte von F .
2
Denition 6 (lfp(F ); gfp(F ))
lfp(F ) := F 1 (;) heit in diesem Fall der kleinste,
gfp(F ) := F 1 (An ) der grote Fixpunkt von F .
Denition 7 (F';A~) Gegeben sei eine Interpretation A~ und eine Formel
' := '(X; xn ), X n-stellig. Dann ist F';A~ deniert durch:
F';A~ : Pot(An ) ! Pot(An )
R 7! fanj A~ j= '(R; an )g
Falls unwichtig ist oder aus dem Kontext klar wird, welche Interpretation A~ gemeint
ist, lassen wir den Index A~ weg und schreiben einfach F' .
11
12
Denition 8 ' := '(X; x) heit induktiv (monoton, antimonoton), wenn fur alle
A~ die Abbildung F';A~ induktiv (monoton, antimonoton) ist.
Denition 9 (Atom) Fur alle Terme r1 ; r2; nt und alle nn-stelligenn 2.Stufe-Variablen
X und Relationssymbole R sind die Formeln r1 =: r2 , Rt und X t Atome (atomare
Formeln).
Denition 10 (PFP-Syntax) Die Syntax der Logik PFP ist durch folgenden Kalkul
gegeben:
' ';
'
'
' wenn ' Atom; :' ; ('^ ) ; 9x' ; [FP n '(X;xn )]nt , wenn X n-stellig.
Xx
Die Symbole 8, _, ! und $ betrachten wir als Abkurzungen. Klammern lassen wir
gerne weg, wenn es die ublichen Vorfahrtsregeln erlauben.
Wenn wir in Zukunft eine Formel Rt, X t oder [FPX x '(X; x)]t hinschreiben,
nehmen wir stillschweigend an, da die Stelligkeit von X bzw. R und die Lange von
x (und t) ubereinstimmen.
Denition 11 (PFP-Semantik) Die Relation A~ j= ist auf die ubliche Weise
induktiv uber den Aufbau von deniert. Im FP-Schritt gilt:
A~ j= [FPX x '(X; x)]t :, F'1(X;x) existiert und enthalt A~(t)
Denition 12 (IFP) IFP ist diejenige Sublogik von PFP, die man erhalt, wenn
man im Kalkul von Denition 10 die FP-Regel auf induktive Formeln '(X; x) einschrankt.
Um IFP-Formeln als solche kenntlich zu machen, schreiben wir auch [IFPX x : : :]
statt [FPX x : : :].
Die Semantik des Fixpunktoperators ist fur IFP-Formeln einfacher, da der Fixpunkt
stets existiert (An ist endlich!). Die Syntax von IFP ist weniger einfach, denn die
Menge der IFP-Formeln ist bedauerlicherweise nicht entscheidbar. Diesen Umstand
kann man beheben, indem man nur Formeln '(X; x) der Gestalt X x _ '0 (X; x)
zulat.
Denition 13 (positiv, negativ) Eine PFP-Formel ' heit positiv (negativ) in
X , falls jedes freie Vorkommen von X in ' im Geltungsbereich einer geraden (ungeraden) Anzahl von Negationszeichen steht.
Denition 14 (LFP) LFP ist diejenige Sublogik von PFP, die man erhalt, wenn
man im Kalkul von Denition 10 die FP-Regel auf Formeln '(X; x) einschrankt,
die positiv in X sind.
Um LFP-Formeln als solche kenntlich zu machen, schreiben wir auch [LFPX x : : :]
statt [FPX x : : :].
Satz 15 Eine LFP-Formel '(X; x) ist monoton (antimonoton), wenn sie positiv
(negativ) in X ist. 2
Aus Satz 15 und Satz 4 folgt:
Satz 16 LFP IFP 2
Der zum LFP-Operator duale GFP-Operator ist in LFP denierbar:
Denition 17 [GFPX x '(X; x)]t := :[LFPX x :'(:X; x)]t
Satz 18 A~ j= [GFPX x '(X; x)]t , A~(t) 2 gfp(F';A~) 2
Kapitel 3
Reduktionen und
vollstandige Probleme
Denition 19 (L-U bersetzung) Gegeben sei eine Signatur ohne Funktionssymbole und eine Logik L. heit (n-stellige) L-U bersetzung von , wenn eine
Abbildung ist, die jedem k-stelligen Relationssymbol R 2 eine L-Formel
R (xn 1 ; : : : ; xn k ) zuordnet, und jeder Konstante c 2 ein Tupel n c von L-Termen.
Im Sinne von Abschnitt 1.2 ist mit L implizit L[ ] gemeint. Eine L-U bersetzung von
ist also in Wirklichkeit eine U bersetzung von in . Eine L[0 ]-U bersetzung von
ist dann eine U bersetzung von in 0 .

Denition 20 (A~ ) Eine n-stellige Ubersetzung
von deniert zu jeder Interpretation A~ eine -Struktur A~ :
Der Trager von A~ ist An
R(A~ ) := RA~(x1 ; : : : ; xk ) fur alle k-stelligen R 2 c(A~ ) := A~(c ) fur alle Konstanten c 2 Wir lassen hier durchaus zu, da R (x1 ; : : : ; xk ) zusatzliche freie Variablen hat. In
diesem Falle hangt A~ von ab. Ebenso durfen in c Variablen vorkommen. Falls
A~ nicht von abhangt, schreiben wir stattdessen auch A .
Denition 21 (L-Reduktion) Sei C eine Klasse von -Strukturen, D eine Klasse

von Interpretation, eine L-Ubersetzung
von .
Dann heit eine L-Reduktion von D auf C , wenn gilt: A~ 2 D , A~ 2 C .
Denition 22 (hart,denierbar,vollstandig) Eine Klasse C von -Strukturen
heit fur eine Logik M
hart bezuglich L-Reduktion
:, fur jede M-Formel gibt es eine L-Reduktion von Mod( ) auf C
denierbar
:, C = Mod() fur ein 2 M
vollstandig (vollstandiges Problem) bezuglich L-Reduktion
:, (i) und (ii) ist der Fall
Man kann auch umgekehrt eine L-U bersetzung zur Expansion von -Formeln verwenden:
13
14

Satz 23 Sei M 2 fPFP, IFP, LFP, FO, QFg und eine M-Ubersetzung
von .
Dann gibt es fur jede Formel 2 M [] eine M-Formel mit A~ j= , A~ j= 2
Die Denition von ist lang und uninteressant, aber an einem Beispiel sieht man
sofort, was gemeint ist:
Beispiel 24 ([FPXx x =: v ^ 9yExy]c) = [FPX x x =: v ^ 9yE (x; y)]c
Fur Informatikerinnen ist also eine U bersetzung so etwas wie eine Makro-Denition.
Mit dieser Vorstellung ist folgender Satz klar:

Satz 25 Sei L 2 fPFP, IFP, LFP, FO, QFg, eine L[0 ]-Ubersetzung
von , 0
0

eine L-Ubersetzung
von .

Dann existiert eine L-Ubersetzung
0 von mit
0 = ( )0
2
Durch die Betrachtung von U bersetzungen als Expansionen von Formeln nden wir
auch einen Zusammenhang zwischen vollstandigen Problemen und Normalformen.
Betrachten wir hierfur ein fur M bezuglich L-Reduktionen vollstandiges Problem
C . C ist deniert durch eine Formel 2 M []. Fur jede M-Formel gibt es eine
L-Reduktion von Mod( ) auf Mod(), d.h. ein mit A~ j= , A~ j= . Nach
Satz 23 ist also =jj= . Da sich (jedenfalls fur L=QF) die alle sehr ahnlich
sind, verdient die Menge der den Namen Normalform.
Wir fassen dies in einem Satz zusammen:
Satz 26 Sei M wie in Satz 23, L eine Sublogik von M und Mod() hart fur M

bezuglich L-Reduktion. Dann ist jede M-Formel aquivalent zu fur eine L-Uber
setzung . Ist 2 M [], so ist f j ist L-Ubersetzung
von g eine Normalform
fur M. 2
Wir werden es im Folgenden nur mit L=QF, also mit QF-U bersetzungen zu tun
haben. Diese nennen wir quantorenfreie U bersetzungen.
Kapitel 4
Spiele
4.1 Denitionen
Wir wiederholen kurz die in der Einleitung gegebenen Regeln des Geographiespiels
auf einer Struktur mit Kantenrelation: Die Spielerinnen ziehen von einer Startposition aus einen Spielstein abwechselnd entlang einer Kante. Wer nicht ziehen kann,
hat verloren.
Wir werden die Geographiespiele und den Begri des Gewinnens jetzt exakt denieren. Dabei werden wir Geographiespiele einfach \Spiele" nennen, und zwar, weil
das Geographiespiel einen Prototyp fur die Strategiespiele fur zwei Personen ohne Zufallselemente darstellt. Sei hierzu S irgend ein solches Spiel (Muhle, Schach,
Halma...). S sei die Menge aller moglichen Stellungen des Spiels. Eine Stellung soll
dabei die gesamte Information uber den Zustand des Spiels wiedergeben, also welche
Figuren im Spiel sind, wo sie stehen, mit welcher Farbe als nachstes gezogen werden
darf usw. Z sei die Menge derjenigen (s1 ; s2 ) 2 S S , fur die die U berfuhrung des
Spiels von der Stellung s1 in die Stellung s2 nach den Regeln des Spiels ein erlaubter
Zug ist. So notiert kann man S als das Geographiespiel auf der Struktur mit Trager
S und Kantenrelation Z auassen1.
Denition 27 (s ) s := fZ; sg, Z zweistelliges Relationssymbol, s Konstante.
Denition 28 (Spiel) Eine s -Struktur S = (S; Z; s) heit Spiel.
Die Elemente von S nennen wir Stellungen, die Elemente von Z die erlaubten Zuge,
und s die Startstellung von S .
Denition 29 (Strategie) Eine Strategie fur ein Spiel S = (S; Z; s) ist eine partielle Abbildung Str : S ! S , deren Graph Teilmenge von Z ist.
D.h. eine Strategie Str bildet Stellungen auf Stellungen ab, so da (a; Str(a)) ein
erlaubter Zug ist. Es handelt sich um eine partielle Funktion, da nicht immer ein
Zug moglich ist. Da eine Strategie fur eine Stellung keinen Zug deniert, erlauben wir in obiger Denition auch dann, wenn einer moglich ware. Man kann das
so interpretieren, da die Spielerin, die diese Strategie verfolgt, in dieser Stellung
aufgibt.
1 F
ur die Endstellungen des Spiels, also solche, die anzeigen, da eine der beiden Parteien
verloren hat, mu man sich die Sache naturlich so zurechtbasteln, da es pat: Zuge in eine solche
Stellung sollen nur erlaubt sein, wenn man mit diesem Zug gewinnt, denn beim Geographiespiel
soll ja gewinnen, wer zuletzt zieht
15
16
Denition 30 (gewinnt, Gewinnstrategie, Gewinnstellung, Verluststellung)
Sei ein Spiel S = (S; Z; s) und eine Stellung a 2 S gegeben.
I gewinnt in a in k Halbzugen
:, Es gibt eine Strategie StrI , so da es fur alle Strategien
StrII eine ungej 1
2
rade Zahl 0 < j < k gibt, fur die StrI (StrII StrI ) (a) existiert, aber
nicht im Denitionsbereich von StrII liegt.
In diesem Fall heit:
{ StrI Gewinnstrategie fur I in a
{ a Gewinnstellung von S .
II gewinnt in a in k Halbzugen
:, Es gibt eine Strategie StrII , so da es jfur alle Strategien StrI eine gerade
Zahl 0 j < k gibt, fur die (StrII StrI ) 2 (a) existiert, aber nicht im Denitionsbereich von StrI liegt.
In diesem Fall heit:
{ StrII Gewinnstrategie fur II in a
{ a Verluststellung von S .
I gewinnt S :, s ist Gewinnstellung von S
II gewinnt S :, s ist Verluststellung von S
Denition 31 (GAME ) Die Menge der Spiele, die I gewinnt, heit GAME .
Bemerkungen:
\I(II) gewinnt a in k Halbzugen" ist oben so deniert, da in Partien, die mit
einer entsprechenden Gewinnstrategie gespielt werden, hochstens k 1 mal
gezogen wird. Der Zug, der nicht mehr moglich ist, wird also mitgezahlt. Dies
hat rechnerische Vorteile.
Eine Quelle moglicher Verwirrung soll hier praventiv genannt werden:
\I gewinnt a" bedeutet nach obiger Denition, da diejenige gewinnt, die am
Zug ist. Einen Halbzug spater ist aber die Andere am Zug. Deshalb wird bei
jedem Halbzug I in II umbenannt und umgekehrt. Dieser Mistand ist hier
nicht vermeidbar, da wir zulassen (und auch verwenden werden), da ein und
die selbe Stellung beiden Spielerinnen zuganglich ist.
Der langen Rede kurzer Sinn: Diejenige die dran ist heit I, nicht diejeige die
am Anfang des Spiels dran war.
Wenn wir die Strategie einer Spielerin uber mehrere Zuge hinweg verfolgen,
werden wir andere Wege nden, diese zu benennen.
4.2 Remisfreie Spiele
Unser Programm ist es (siehe Einleitung) zu zeigen, da GAME vollstandig fur
IFP bezuglich quantorenfreier Reduktion ist, um daraus Normalformen fur IFP zu
gewinnen, die IFP=LFP beweisen. Hierbei ergibt sich eine Komplikation: Will man
durch Induktion fur jede IFP-Formel eine quantorenfreie Reduktion auf GAME
angeben, bekommt man Schwierigkeiten mit der Negation. Denn die Negation von \I
gewinnt S " ist nicht \II gewinnt S ". Denn nicht in jeder Stellung gibt es fur eine der
17
beiden Parteien eine Gewinnstrategie. Anders ausgedruckt: Remis ist moglich. Die
Schwierigkeit besteht also darin, zweiwertige Formeln (wahr/falsch) auf dreiwertige
Spiele (gewinnt/remis/verliert) abzubilden. Der listige Ausweg besteht darin, sich
auf Spiele zu beschranken, bei denen Remis nicht moglich ist.
Denition 32 (Remisstellung, entschieden, remisfrei)
Fur ein Spiel S = (S; Z; s) heit a 2 S Remisstellung, wenn a weder Gewinn- noch
Verluststellung ist.
S heit entschieden, wenn s keine Remisstellung ist.
S heit remisfrei, wenn kein a 2 S Remisstellung ist.
An dieser Stelle ist es wichtig, kurz uber den Unterschied zwischen den Eigenschaften \entschieden" und \remisfrei" zu meditieren. Nicht alle entschiedenen Spiele
sind remisfrei.
Denition 33 (RF ) RF ist die Menge der remisfreien Spiele.
4.3 Der Hauptsatz
Unsere zentrale Behauptung ist es, da man tatsachlich mit remisfreien Spielen
auskommt. Genauer gesagt, da GAME hart fur IFP ist, und zwar vermittels solcher
quantorenfreier Reduktionen, die auf remisfreie Spiele abbilden.

Denition 34 Eine Ubersetzung
von s heit remisfrei (entschieden), wenn fur
~
~
alle A das Spiel A remisfrei ist.

Hauptsatz 35 Fur jede IFP-Formel gibt es eine remisfreie quantorenfreie Ubersetzung von s , die eine Reduktion von Mod( ) auf GAME ist.
Zusatz: Man kann mit s = d~ wahlen.
Es folgt sofort:
Korollar 36 GAME ist hart fur IFP bezuglich quantorenfreier Reduktion. 2
Korollar 37 RF \ GAME ist hart fur IFP bezuglich quantorenfreier Reduktion.
2
Korollar 37 ist um eine Spitzndigkeit schwacher als der Hauptsatz: Der Hauptsatz
liefert fur jede IFP-Formel eine quantorenfreie U bersetzung mit
A~ ist remisfrei ^ (I gewinnt A~ , A~ j= ),
Korollar 37 liefert higegen mit
(A~ ist remisfrei ^ I gewinnt A~ ) , A~ j= .
Wir werden zwei Beweise fur den Haupsatz angeben. Der erste, \vorlauge" (im
Kapitel Zwischenspiel) verwendet, da GAME hart fur IFP ist. D.h. er reduziert Spiele auf remisfreie Spiele. Er ist also nicht tauglich fur unser Programm,
einen neuen Beweis fur IFP=LFP zu liefern. Wir fuhren ihn trotzdem aus, weil
er anschaulich ist und Konzepte klar macht, die im zweiten \endgultigen" Beweis
benutzt werden.
Im ubrigen ist der Hauptsatz starker formuliert als notwendig ist, um daraus IFP=LFP
zu erhalten. Hierfur ware es ausreichend, entschiedene Spiele zu betrachten, wodurch
sich der Beweis (geringfugig) vereinfachen wurde. Da es dennoch interessant ist,
die Spiele remisfrei zu halten, zeigt die Anwendung in Kapitel 9.
18
Kapitel 5
Diagramme
5.1 Denition
Fur den Beweis des Hauptsatzes werden wir zu jeder IFP-Formel eine quantorenfreie U bersetzung von s angeben mussen. Da dies zu recht langen und unleserlichen
quantorenfreien Formeln fuhrt, werden wir so vorgehen: Wir wandeln IFP-Formeln
zunachst in (noch zu denierende) Diagramme um und geben eine Vorschrift an,
wie man aus einem solchen Diagramm eine quantorenfreie U bersetzung von s gewinnt. Stellvertretend fur die zugehorige U bersetzung von s wird ein Diagramm
zu jeder Struktur ein Spiel denieren, das uber die Gultigkeit der einer IFP-Formel
entscheidet.
Diagramme haben den Vorteil, da sie leichter zu lesen und beweistechnisch leichter
handhabbar sind als quantorenfreie U bersetzungen.
Denition 38 (Diagramm) Ein -Diagramm D besteht aus einer endlichen Menge von Feldern und einer Menge von beschrifteten oder unbeschrifteten Pfeilen zwischen diesen Feldern. Eines der Felder ist mit \Start" beschriftet und heit das
Startfeld von D. Die Beschriftung jedes beschrifteten Pfeils hat eine der folgenden
Formen:
\v?" fur ein Tupel v von Variablen
\v := t" fur gleichlange Tupel v von Variablen und t von Termen.
\ !" fur ein 2 QF[].
Wenn die Signatur eines Diagramms nicht explizit genannt wird, meinen wir ein
-Diagramm.
Beispiel 39
D(v; w) :=
6x =: w!
- y? 6
j
-
Start xy := vv
j
j
j
x := y
ist ein fE g-Diagramm.
19
-
:Exy !
j
j
20
Denition 40 (Figur von D) Sei D ein Diagramm. Dann heien die Variablen,
die in einer Beschriftung \x?" oder \x := t" im Tupel x auftauchen, Figuren von
D.
Zu Beispiel 39: Die Figuren von D(v; w) sind x und y.
Denition 41 (A~D ) Ein -Diagramm D deniert zu jeder -Interpretation
A~ = (A; ) ein Spiel A~D :
Die Stellungen dieses Spiels sind die Paare ( f ; ), wobei f ein Feld von D ist
und eine A-Belegung, die alle Variablen auer den Figuren von D so belegt
wie (D.h wenn x die Figuren von D sind, so ist = [ xa ] fur irgendwelche
Elemente a von A).
Die Startstellung ist (Start,).
(( f ; ); ( f 0; 0 )) ist ein erlaubter Zug,
wenn es in D einen Pfeil von f nach f 0 gibt so da eine der folgenden
Aussagen zutrit:
{ Der Pfeil ist unbeschriftet und 0 = .
{ Der Pfeil ist mit \v?" beschriftet und 0 = [ va ] fur irgendwelche a 2 A.
{ Der Pfeil ist mit \v := t" beschriftet und 0 = [ v(t) ]
{ Der Pfeil ist mit \ !" beschriftet, 0 = und (A; ) j=
Man stellt sich das Spiel A~D am besten so vor:
Gespielt wird auf einem Spielbrett, das aus zwei Teilen besteht, A und D. Die
Figuren von D sind Spielguren, die sich auf A bewegen, d.h. die Elemente von A
sind die moglichen Positionen dieser Spielguren. Ein zusatzlicher Spielstein bewegt
sich nur auf den Feldern von D. Er wird von den beiden Spielerinnen abwechselnd
entlang eines Pfeils gezogen. Die Beschriftung des Pfeils gibt an, wie wahrenddessen
die Figuren auf A von der jeweiligen Spielerin bewegt werden durfen. Lies \v?" als
\Stelle die Figuren v in beliebige Positionen" und \v := t" als \Stelle die Figuren v
in die Positionen t". Entlang eines mit \ !" beschrifteten Pfeiles darf nur gezogen
werden, wenn fur die aktuelle Position der Figuren erfullt ist.
Wer nicht mehr ziehen kann, hat verloren.
i
i
i
i
i
i
Beispiel 42 Fur das Diagramm D(v; w) aus Beispiel 39 und fur alle fE g-Interpretationen
G~ = (G ; ) gilt:1
I gewinnt G~D(v;w) , es gibt einen Weg von (v) nach (w)
Anders ausgedruckt: I gewinnt G~D(v;w) , G~ j= (v; w), mit
(v; w) := [IFPXx x =: w _ 9y(Exy ^ Xy)]v
An diesem Beispiel kann man die Rolle der verschiedenen Variablen in Diagrammen
studieren.
Die Belegung von v und w andert sich wahrend des Spiels nicht. Wer das Spiel gewinnt, hangt davon ab, wie v und w durch die vorgegebene Belegung interpretiert
werden. Dies entspricht der Tatsache, da v und w frei in (v; w) sind.
1 Das Beispiel funktioniert nat
urlich nur, wenn x, y, v und w tatsachlich verschiedene Variablen
bezeichnen. Wir nehmen ab jetzt stets an, da je zwei verschiedene Variablennamen, die zusammen
explizit in einem Diagramm auftauchen, dort auch verschiedene Variablen bezeichnen (damit das
nicht falsch verstanden wird: zwei verschiedene Variablen konnen naturlich gleich belegt werden.).
21
Die Figuren x und y von D(v; w) entsprechen gebundenen Variablen von (v; w).
Ihre Belegung andert sich im Laufe des Spiels. Wer das Spiel gewinnt, hangt nicht
von (x) und (y) ab. Wir werden Diagramme in der Regel so angeben, da der
Ausgang des Spiels nicht davon abhangt, wie die Figuren zu Beginn des Spiels belegt
sind. Diagramme, die das beachten, nennen wir \brav":
Denition 43 (brav) Ein Diagramm D heit brav, wenn fur alle A~, jede Figur
x von D und alle a 2 A gilt:
I (II) gewinnt A~D , I (II) gewinnt A~[ x ]D
a
Da ein Diagramm brav ist, erreichen wir dadurch, da wir jeder Figur x durch eine
Beschriftung \x := t" einen sinnvollen Anfangswert zuweisen, bevor sie anderweitig
benutzt wird.
Denition 44 Ein Diagramm D heit remisfrei (entschieden), wenn fur alle Interpretationen A~ das Spiel A~D remisfrei (entschieden) ist.
5.2 Diagramme und quantorenfreie U bersetzungen

Satz 45 Fur jedes brave Diagramm D gibt es eine quantorenfreie Ubersetzung
von s mit
I (II) gewinnt A~ , I (II) gewinnt A~D
und s = d~. Wenn D remisfrei ist, ist auch remisfrei.
Beweis: Wir verzichten auf einen formalen Beweis und zeigen an unserem Beispiel
D(v; w), wie man ein Diagramm in eine quantorenfreie U bersetzung umsetzt:
Numeriere zunachst die Felder des Diagramms, das Startfeld erhalt die Nummer 0.
D(v; w)
5
6x =: w!
Start xy := vv
- 1 - 2 y? - 3 :Exy-! 4
0
j
j
j
6
j
j
j
x := y
Setze nun
6
u6 0 x0 y0 ) = (\u6 = 0" ^ \u6 0 = 1" ^ x0 =: v ^ y0 =: v
Z (uxy;
_ (\u66 = 1" ^ \u66 0 = 2" ^ x0 =: x ^ y0 =: y
_ (\u6 = 2" ^ \u6 0 = 3" ^ x0 =: x
_ (\u6 = 3" ^ \u6 0 = 4" ^ x0 =: x ^ y0 =: y ^ :Exy
_ (\u6 = 3" ^ \u6 0 = 2" ^ x0 =: y ^ y0 =: y
_ (\u= 2" ^ \u0 = 5" ^ x0 =: x ^ y0 =: y ^ x =: w
Hierbei sei
V
:
k=0
\u6 = k" := (V0<j<6 uu0 ==: uuj ) ^ u 6=: u falls
falls
0<k<6
j
0
k
0
0<j<k
)
)
)
)
)
)
22
Jedes Disjunktionsglied der Formel Z (u6 xy; u6 0 x0 y0 ) entspricht einem Pfeil im Diagramm und gibt an, welche Bewegungen des Spielsteins und der Figuren durch den
Pfeil erlaubt werden.
Die erlaubten Zuge in G~ entsprechen also erlaubten Zugen in G~Dvw und umgekehrt. Man beachte, da in jeder Interpretation fur genau ein 0 k < 6 die
Formel \u6 = k" erfullt ist. Deshalb korrespondiert jede Stellung von G~ zu einer
von G~D(v;w) . Setzt man auerdem s := dddddddd, beginnt das Spiel tatsachlich bei
Start (denn in jeder Interpretation gilt u6 =: dddddd ! \u6 = 0").
Da das Diagramm brav ist, kommt es auf die Startposition von x und y nicht an,
wir konnen also ebenfalls jeweils d wahlen.
Dieses Verfahren lat sich ohne weiteres auf jedes brave Diagramm ubertragen. 2
5.3 Subdiagramme
Bei der Wiedergabe von Diagrammen werden wir bereits denierte Diagramme
als Subdigramme verwenden. Pfeile, die in ein solches Subdiagramm fuhren, sollen
dabei immer an dessen Startfeld enden.
Beispiel 46 Fur das Diagramm
Dzsh :=
Start
j
-
j
vw?-D(v; w)
und alle Graphen G gilt:
D , G ist zusammenhangend.
I gewinnt Gzsh
Auerdem wollen wir auch Pfeile wieder aus einem Subdiagramm herausfuhren.
Dazu werden wir in diesem ein Exitfeld ausweisen, an dem alle Pfeile starten, die
aus dem Subdiagramm herausfuhren.
Kapitel 6
Zwischenspiel
In diesem Kapitel skizzieren wir einen Beweis fur folgenden Satz:
Satz 47 Es gibt eine remisfreie quantorenfreie Reduktion von GAME 1 auf GAME .
Aus Satz 47 kann man den Hauptsatz (ohne den Zusatz) folgern, wenn man voraussetzt, da folgende Behauptung schon bewiesen ist:
(}) GAME ist hart fur IFP bezuglich quantorenfreier Reduktion.
Beweis des Hauptsatzes auf Basis von (}) und Satz 47: Sei eine IFPFormel. (}) liefert eine quantorenfreie Reduktion von Mod( ) auf GAME , Satz
47 eine remisfreie quantorenfreie Reduktion 0 von GAME auf GAME . Dann ist
0 eine remisfreie quantorenfreie Reduktion von Mod( ) auf GAME .
2
Im nachsten Kapitel werden wir den Hauptsatz direkt beweisen, woraus (}) sofort
folgt (in der Tat haben wir (}) schon Korollar 36 genannt). Man erhalt (}) aber
auch aus Normalformsatzen fur IFP (z.B. in [Dah87] oder auch Bemerkung 57).
Beweis (-Skizze) fur Satz 47 Nach Satz 45 genugt es, ein remisfreies braves
s -Diagramm Drf anzugeben mit2
I gewinnt S , I gewinnt S Drf
Die Felder aller Diagramme in diesem Kapitel sind schwarz-wei gefarbt. Wir stellen uns hierzu vor, da das Spiel S Drf von zwei Spielerinnen namens \Wei" und
\Schwarz" gespielt wird. Auf Grund der alternierenden Farbung ist Wei immer auf
den weien Feldern am Zug, Schwarz auf den schwarzen. Wei beginnt. Wir basteln
Drf also so, da Wei das Spiel S Drf gewinnt, wenn I das Spiel S gewinnt.
Um das Spiel remisfrei zu machen, mussen wir es auf irgend eine Weise in der
Lange beschranken. Auf geordneten Strukturen ist dies einfach. Man kann eine Figur als Zahler verwenden, der bei jedem Halbzug dekrementiert wird. Ist der Zahler
1 Wir hatten Reduktionen so deniert, da von einer Klasse von Interpretationen auf eine Klasse
von Strukturen reduziert wird. Korrekter muten wir also denieren:
g := f(S ; ) j S 2 GAME ; s -Belegungg
GAME
und Satz 47 so formulieren:
g auf GAME .
Es gibt eine remisfreie quantorenfreie Reduktion von GAME
2 Im Sinne der vorigen Funote m
uten wir hier eigentlich \I gewinnt S , I gewinnt S~Drf "
schreiben. Wir mussen darauf achten, da der Ausgang des Spiels S~Drf nicht von der zur Interpretation S~ gehorigen Belegung abhangt. Dies ist gewahrleistet, wenn alle Variablen, die in Drf
auftauchen, Figuren sind und Drf brav ist.
23
24
abgelaufen bevor jemand gewonnen hat, so gewinnt Schwarz.3 Auf ungeordneten
Strukturen fehlt uns die Moglichkeit zu zahlen. Wir brauchen also eine andere Art
der Zeitmessung. Hierzu verwenden wir ein parallel gespieltes Spiel grotmoglicher
endlicher Lange (auf der selben Struktur S ). Um zwei parallel gespielte Spiele innerhalb von S Drf simulieren zu konnen, denieren wir zwei Bausteine:
1 Runde(x) :=
1 Runde(y) :=
Start
Start
j
j
w?
?:Zxw-!
z
j
x?
?:Zwx-!
j
?
z
Exit
?
z
w?
z
?:Zyw-!
j
z
y?
?:Zwy-!
z
Exit
j
Man mache sich klar, da diese beiden Diagramme jeweils eine Runde (d.h. zwei
Halbzuge) im ursprunglichen Spiel S simulieren, wobei x (bzw. y) auf dem Startfeld
mit der Stellung vor dieser Runde belegt ist, auf dem Exitfeld mit der Stellung nach
dieser Runde. w ist eine Hilfsvariable und taucht auerhalb dieser Subdiagramme
nicht auf.
Man bemerke, da in 1 Runde(x) Wei zuerst zieht, in 1 Runde(y) hingegen
Schwarz (im simulierten Spiel, nicht im Diagramm!).
Zu Zwecken des Vergleichs der beiden Spiele brauchen wir noch folgende Denition:
Fur eine Stellung a 2 S sei
l(a) :=
minfk j I gewinnt S in a in 2k Halbzugeng; falls a Gewinnstellung
sonst
1
l(a) nennen wir die \Lange" von a. Die Lange einer Stellung ist also die Anzahl der
Runden, die bei optimaler Strategie schlimmstenfalls notig ist, um das Spiel von
dieser Stellung aus zu gewinnen.
Man uberlege sich, da Wei in 1 Runde(x) gewinnt, wenn zuvor l(x) = 1 war.
Schwarz gewinnt in 1 Runde(y) , wenn zuvor l(y) = 1 war.
Wir betrachten nun zunachst ein entschiedenes Diagramm Dent mit der Eigenschaft
() I gewinnt S , I gewinnt S Dent
um dieses dann nachtraglich zu einem remisfreien Diagramm auszubauen.
3 F
ur geordnete Strukturen zeigt man auf diese Weise leicht, da schon die azyklichen Spiele
vollstandig fur IFP bezuglich quantorenfreier Reduktion sind.
25
Dent :=
Start
j
x := s
? -
z
y?
?
j
j
x? -
z
- 1 Runde(x) -
j
x?
?xy := yx
z
?
?
1 Runde(x)
1 Runde(y)
- j
- z
?
1 Runde(x)
?
@@
1 Runde(y)
Um das Spiel S Dent zu verstehen, bilden wir dieses Diagramm in einer kommentierten Version auf der nachsten Seite nochmal ab.
26
Dent , kommentiert
wei: \Die Lange von
endlich."
x = s ist
schwarz: \Die
Lange von x =
s ist unendlich,
weil es in S keine Gewinnstellung gibt."
Start
j
`
`
`
x := s
`
`
`
`
`
`
`
j
y?
?
x?
j
schwarz: \x ist
wei: \y ist
nicht kurzer
als x"
`
`
`
um mehr als 1
langer als y. Du
bekommst eine
Runde Vorsprung
und verlierst den
Vergleich"
x? -
- 1 Runde(x) `
`
`
`
z
`
`
`
`
`
maximaler endlicher Lange und
trotzdem kurzer als x"
\Es gibt Gewinnstellungen in S ,
x ist eine der
Lange 1."
`
? -
schwarz: \y ist eine Stellung mit
wei:
z
j
wei: \y ist zwar kurzer als x
und hat endliche Lange, aber
nicht maximale. Ich zeige dir eine neue Stellung x, die um genau
1 langer ist als y."
?xy := yx
schwarz:
\x ist nicht langer
als y. Wir tauschen
?
die Stellungen, ich
1 Runde(y) bekomme eine Runde Vorsprung und
gewinne den Vergleich"
`
`
z
`
`
`
`
`
`
?
1 Runde(x)
`
`
`
`
`
`
`
`
`
`
`
`
`
`
-
`
`
`
`
`
`
j
- z
?
1 Runde(x)
?
@@
1 Runde(y)
Vergleich
Diese Schleife ist ein Vergleich
der Langen von x und y. Wei
gewinnt, wenn l(x) < 1 und
l(x) (y) war (vor Eintritt in
die Schleife). Schwarz gewinnt,
wenn l(y) < 1 und l(y) < l(x)
war.
Die Texte im Diagramm sind als Dialoge zu lesen. Sie geben das wieder, was die
jeweilige Spielerin durch die Benutzung des zugehorigen Pfeiles implizit behauptet.
Zu Beginn des Spiels steht Aussage gegen Aussage: Wei behauptet \I gewinnt S ",
Schwarz behauptet, da das nicht der Fall ist.
Man prufe nach, da
jede Behauptung die zuvor von der Gegnerin aufgestellte Behauptung widerlegt,
im Fall, da eine Behauptung falsch ist, sie in einer der angegebenen Weisen
widerlegt werden kann,
jede der beiden Spielerinnen in der Vergleichsschleife (unten) gewinnen kann,
wenn sie mit allen Behauptungen recht hatte.
27
Auf diese Weise sollte es klar werden, da Dent () erfullt und entschieden ist.
Nun ist aber Dent nicht remisfrei, denn dazu durfte keine Stellung ( f ; ) von S Dent
eine Remisstellung sein. Sei nun f z.B. das erste Feld der Vergleichsschleife, und belege x und y mit Remisstellungen (von S ). Dann ist oensichtlich ( f ; ) Remisstellung von S Dent .
Wir mussen Schwarz also in jeder Runde von neuem die Gelegenheit geben, x als
Remisstellung zu entlarven. Dies leistet das folgende Diagramm Drf :
i
i
i
Drf
Start
j
x := s
-? z
y?
?
j
j
x? -
z
- 1 Runde(x) -
j
x?
?xy := yx
z
?
?
1 Runde(x)
1 Runde(y)
- j
- z
?
1 Runde(x)
?
@@
?
1 Runde(y)
j
Schwarz kann im Spiel S Drf nach jedem beliebigen Durchlauf der Vergleichs-Schleife
das zuvor dargestellte Verfahren bemuhen, um zu gewinnen, wenn x keine Gewinnstellung in S ist. Wenn hingegen x eine Gewinnstellung in S ist, kann Schwarz
das Spiel nicht dadurch verzogern, da sie dieses Verfahren von vorne aufrollt:
Wahlt sie l(y) l(x), so kann dies von Wei ignoriert werden (linker Pfeil). Wahlt
sie l(y) < l(x), so mu Wei zwar den rechten Pfeil nehmen, wahlt aber x mit
28
l(x) = l(y) + 1, also jedenfalls so, da die Lange von x nicht groer ist als vorher.
Wei verliert also nichts, wenn x Gewinnstellung war.
Ich hoe, diese Skizze hat es einigermaen klar gemacht, da Drf tatsachlich das
gewunschte leistet. Die Tatigkeit des induktiven Angebens von Gewinnstrategien,
wie sie fur einen exakteren Beweis notwendig ware, wollen wir hier nicht uben, da
wir ihrer schon im nachsten Kapitel in ermudender Ausfuhrlichkeit huldigen werden.
Kapitel 7
Beweis des Hauptsatzes
Satz 48 Fur jede IFP-Formel gibt es ein braves, remisfreies Diagramm D mit
I gewinnt A~D , A~ j=
Aus diesem Satz folgt mit Satz 45 der Hauptsatz (inclusive Zusatz). Der Rest des
Kapitels besteht aus dem Beweis von Satz 48.
Wir denieren D induktiv uber den Aufbau von :
(b) falls = :'
D :=
(a)falls Atom
D :=
Start
j
!-
Start
j
(c) falls = (' ^ )
D :=
Start
j
*
- H
HHH
j
j
-
D'
(d) falls = 9x'
D :=
D'
Start x?
j
j
D
29
-
j
-
D'
30
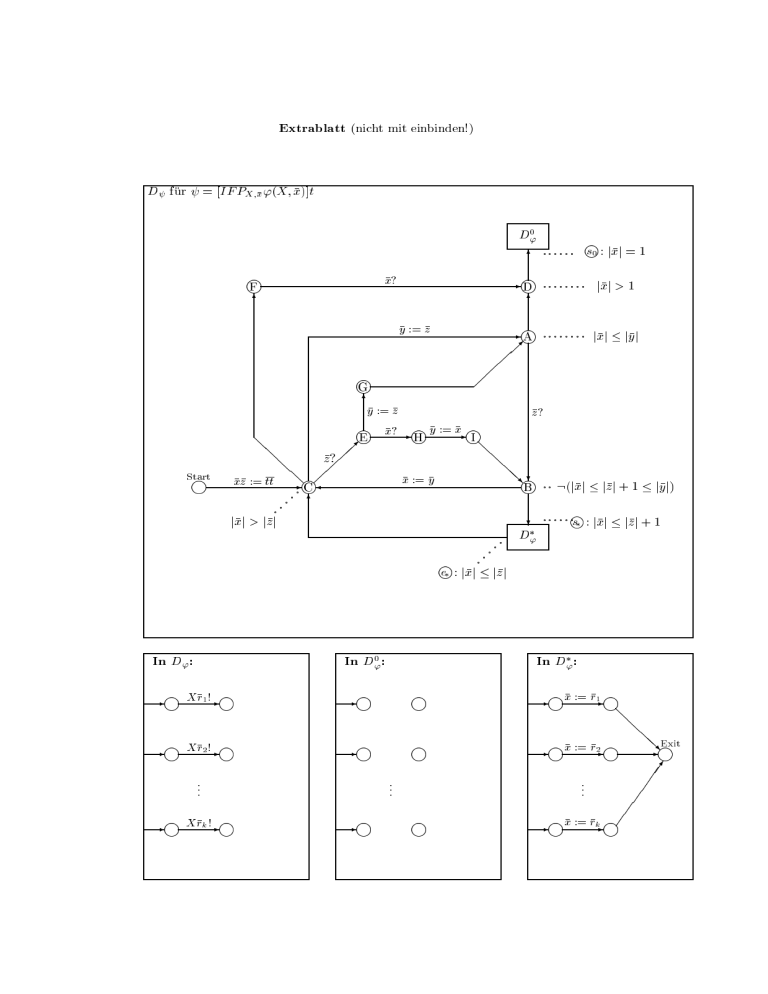
(e) falls = [IFPX x '(X; x)]t
D :=
D'0
6
-D
6
-A
x?
F
6
j
j
y := z
j
G
6y := z
y := x
E x? - H
I
j
Start
j
@@
xz := tt
z?
@@
-C
6
j
j
j
x := y
z?
@@
@@R ?
B
j
j
?
D'
y und z seien Tupel von Variablen, die in D' nicht vorkommen. Ihre Lange sei
die selbe wie die von x.
D'0 sei das Diagramm, das aus D' entsteht, wenn man fur alle Terme r jeden
mit \X r!" beschrifteten Pfeil entfernt.
D' sei das Diagramm, das aus D' entsteht, wenn man
{ ein neues Feld namens Exit (bzw. Exitfeld) hinzufugt,
{ fur alle Terme r jeden mit \X r!" beschrifteten Pfeil durch einen Pfeil
ersetzt, der mit \x := r" beschriftet ist,
{ von jedem Feld, das am Ende eines solchermaen abgeanderten Pfeiles
liegt, einen Pfeil zum Exitfeld hinzufugt.
Siehe auch die Skizze auf der nachsten Seite.
Die Konstruktion von D'0 und D' mag hier etwas seltsam anmuten. Diese Subdiagramme werden in U bung 2 auf Seite 33 naher erlautert. Hier sei soviel verraten,
da D'0 die Formel '(;; x) vertritt und D' die Abbildung F' .
Aus der Konstruktion wird klar, da in jedem der induktiv denierten Diagramme
Beschriftungen der Form \ !" nur mit atomarem vorkommen, und da solchermaen beschriftete Pfeile immer an einem Feld enden, von dem aus es nicht mehr
weiter geht.
Folgende Skizze gibt also die Verhaltnisse in D' korrekt wieder:
31
Vorher (in D')
Nachher (in D' )
-
-
-
j
j
X r1!
X r2!
j
X rk!
j
j
j
..
.
-
x := r1
@@
@-@RExit
- x := r-
..
.
- x := r-k j
2
j
j
j
j
j
j
Wir erinnern uns auerdem, da der Pfeil von D' nach C (im Diagramm auf der
vorigen Seite) am Exitfeld von D' anfangt (siehe Abschnitt 5.3).
Soweit die Denition der Diagramme.
In den Fallen (a) bis (d) sieht man sofort, da D die geforderten Eigenschaften
erfullt, wenn sie fur D' (und D ) gelten.
Bleibt also Fall (e). Fur den Rest des Kapitels sei = [IFPX;x '(X; x)]t und D
das zugehorige Diagramm. D ist oensichtlich brav, wenn D' brav ist. Wir mussen
noch zeigen, da das Diagramm D remisfrei ist und da gilt:
I gewinnt A~D , A~ j=
i
Als Induktionsvoraussetzung haben wir, da D' remisfrei ist und da gilt:
I gewinnt A~D' , A~ j= '(X; x)
Ebenfalls fur den Rest des Kapitels sei A~ fest gewahlt.
s0 und s seien die Startfelder von D'0 bzw. D' , e das Exitfeld von D' .
i
i
i
Um das Spiel A~D zu erklaren denieren wir Xk := F'k (;) (die Xk sind also die
Iterationsstufen von X in ). Auedem sei
k , wenn a 2 Xk nXk 1
jaj := 1
, wenn a 2= X1
Wir schreiben auch j= jxj = k statt j (x)j = k, j= jxj jyj statt j (x)j j (y )j
usw. Wenn wir uns auf eine bestimmte Stellung ( f ; ) beziehen, schreiben wir auch
einfach, da die Gleichung/Ungleichung gilt, und meinen damit, da diese erfullt.
Wir verwenden die ublichen Konventionen fur 1, insbesondere gilt k < 1 fur alle
k 2 IN .
Ab hier wird der Beweis sehr formal, langlich und wenig aufschlureich. Deshalb
schieben wir zunachst ein paar U bungen ein, anhand derer die Leserin das Diagramm D verstehen kann. Der Vorteil dieses Vorgehens ist, da ich Erklarungen
in einer Reihenfolge angeben kann, die zwar beweistechnisch ungunstig ist, aber von
hoherem Erklarungswert. Wer nicht mit U bungen behelligt werden will, kann auf
Seite 35 weiterlesen.
i
32
U bungen
In diesen Ubungen erlauben wir uns, auer quantorenfreie Formeln auch andere
Bedingungen an an die Pfeile zu schreiben. \jxj = 1!" heit hier z.B: dieser Pfeil
darf nur gezogen werden, wenn jxj = 1.
U bung 1: Zeigen Sie fur das folgende Diagramm D1, da es remisfrei ist und da
fur alle gilt:
(i) I gewinnt in ( A ; ) , j= jxj jyj ^ jxj < 1
(ii) I gewinnt in ( B ; ) , j= (jyj jzj ^ jyj < 1) _ (jxj > jzj + 1 _ jxj = 1)
(iii) I gewinnt in ( C ; ) , j= jxj > jzj _ j xj = 1
D1 :=
i
i
i
D
6jxj = 1!
j
-A
y := z
j
z?
Start
j
xz := tt
-C
j
E
j
jxj = 1!
?
x := y
B
j
?
Z
jx
j > jzj + 1
_ jx
j = jzj = 1!
j
Hinweis: Man uberlege sich dies zunachst fur Stellungen, in denen x, y und z endlich sind, und zwar mit folgender Idee: In jeder Runde A !B !C !A tauschen
die Spielerinnen die Rollen. Immer abwechselnd darf im Zug A ! B ein Tupel
z gewahlt werden. Dieses darf dem Betrag nach um hochstens 1 kleiner sein, als
das von der selben Spielerin 2 Runden zuvor gewahlte (welches inzwischen x heit),
sonst bestraft das die Gegnerin mit einem Zug nach Z . Wer zuerst beim Betrag
1 angekommen ist kann das nachste mal nach D ziehen und gewinnen. Auf diese
Weise werden die Betrage zweier Tupel verglichen.
i
i
i
i
i
i
Bemerkung: Aus (iii) kann schlieen, da gilt:
I gewinnt AD1 , t 2 X1 (, A~ j= )
i
i
33
U bung 2: Zeigen Sie dasselbe fur D2:
D2 :=
D'0
6
D
6
j
y := z
-A
j
z?
Start
j
xz := tt
-C
6
j
E
j
jxj = 1!
x := y
?
B
j
?
D'
Hinweise:
Da in D'0 genau die Kanten geloscht sind, die in D' mit \X r!" beschriftet
waren, gilt:
0
I gewinnt (A; )D' , I gewinnt (A; [ X; ])D'
, (A; [ X; ]) j= ' (das hatten wir fur D' vorausgesetzt)
, jxj = 1
Der Zug nach D ist also genau dann vorteilhaft, wenn jxj = 1.
Wer auf dem Exitfeld von D' am Zug ist, gewinnt, wenn jzj endlich ist, genau
dann, wenn jxj jzj (also wenn x 2 Xjzj ), weil es noch zwei Zuge bis A sind.
Wenn man sich die Denition von D' ansieht, sieht man, da deshalb
I gewinnt ( s ; ) , I gewinnt (A; [ XXjzj ])D'
, (A; [ XXjzj ]) j= '
, jxj jzj + 1
Wenn jzj endlich ist, ist der Zug nach s also genau dann vorteilhaft, wenn
jxj jzj + 1. Wenn jzj = 1 ist, argumentiere entsprechend fur X1 .
Man mache sich klar, da es sich bei der Argumentation im vorigen Punkt
nicht um einen Zirkelschlu handelt, weil die Voraussetzung fur A nur fur
den nachstkleineren Betrag von x benotigt wird.
i
i
i
i
i
34
U bung 3: Zeigen Sie dasselbe fur D auf Seite 30 (oder auf dem Extrablatt).
Hinweis: Wer auf C mit jxj = 1 am Zug ist, zieht nach F , wenn X1 = ;,
andernfalls nach E und wahlt z so da jzj endlich, aber maximal ist. Aus (i) und
(ii) folgt, das keine mogliche Gegenstrategie eine Chance hat (verwende jxj = 1!).
Ist umgekehrt jxj < 1, so bringt der Zug nach E keine Vorteile. Falls dabei z mit
jzj < jxj gewahlt wird, kann die Gegnerin nach H ziehen und x mit jxj = jzj + 1
i
i
i
i
i
wahlen, andernfalls kann sie nach G ziehen.
Bemerkung: Wie schon in U bung 1 bemerkt erhalt man aus (iii):
A~D , A~ j= ;
i
also das, was zum Beweis des Hauptsatzes noch fehlt.
35
Wer die U bungen erfolgreich absolviert hat, darf auf Seite 39 weiterlesen. Wer nicht,
mu mit mir durch einen kleinen Morast von Hilfssatzen waten.
Wir erinnern uns kurz an die Situation vor Einschub der U bungen:
Wir haben = [IFPX;x '(X; x)]t und D das zugehorige Diagramm (auf Seite 30
oder auf dem Extrablatt). Wir mussen zeigen, da das Diagramm D remisfrei ist
und da gilt:
I gewinnt A~D , A~ j=
Als Induktionsvoraussetzung haben wir die entsprechenden Eigenschaften fur D' .
A~ ist fest gewahlt. s0 und s sind die Startfelder von D'0 bzw. D' , e das Exitfeld
von D' .
Stellungen seien ab jetzt, wenn nichts anderes gesagt wird, Stellungen von A~D ,
Belegungen A-Belegungen.
i
i
i
Hilfssatz 1 Fur alle f 2 D'0 und alle gilt:
I (II) gewinnt in ( f ; ) (im Spiel A~D )
, I (II) gewinnt in ( f ; [ X; ]) im Spiel A~D'
Beweis: Da X in D nicht vorkommt,
spielt die Belegung von X im Spiel A~D
X
i
i
i
keine Rolle. O.B.d.A ist also = [ ; ]. D'0 unterscheidet sich von D' nur durch
die weggelassenen Pfeile, die in D' mit X r! beschriftet sind. Diese durfen aber mit
(X ) = ; sowieso nicht gezogen werden.
2
Hilfssatz 2 I gewinnt in ( s0; ), wenn j= jxj = 1, II sonst.
Beweis: jxXj=1 bedeutet nach Denition dasselbe wie (A; ) j= '(;; x),
bzw. (A; [ ; ]) j= '. Nach der Induktionsvoraussetzung gilt dies genau dann, wenn
I gewinnt (A; [ X; ])D' , Nach Hilfssatz 1 ist dies genau dann der Fall, wenn ( s0; )
Gewinnstellung von A~D . Da andernfalls II gewinnt, folgt aus der Remisfreiheit
i
i
2
von D'.
Rezept 49 (Schokoladenmakronen I [Haa94])
8 groe Eiklar
500g Puderzucker
500g Mandeln
100-200g SchmelzSchokolade
1 Vanillezucker
Man stellt mit ungeschalt geriebenen Mandeln und geriebener Schokolade eine Makronenmasse her. Mit zwei
Kaeeloeln formt man Makronen.
8 Eiklar
500g Sandzucker
1 Zitronensaft
500g Mandeln
300g Schokolade
Bei dieser Makronenmasse geht man von ungeschlagenem Eiklar aus. Die Mandeln werden nicht geschalt.
Man formt kleine Kugeln.
Rezept 50 (Schokoladenmakronen II [Haa94])
Hinweis: Man erhalt 80-90 Stuck
[Haa94] gibt fur Makronen 30-45 Minuten Backzeit bei 140 160C an, zuzuglich
5-10 Minuten Nachhitze.
36
Hilfssatz 3 Fur alle k 2 IN gilt:
(i) I gewinnt in ( A ; ), wenn j= jxj k ^ jxj jyj
(ii) II gewinnt in ( C ; ), wenn j= jxj k ^ jxj jzj
(iii) I gewinnt in ( e ; ), wenn j= jxj k ^ jxj jzj
(iv) I gewinnt in ( B ; ), wenn j= jyj k ^ :(jxj jzj + 1 jyj)
(v) II gewinnt in ( A ; ), wenn j= jyj k ^ jxj > jyj
(vi) I gewinnt in ( C ; ), wenn j= jzj k ^ jxj > jzj
(vii) II gewinnt in ( e ; ), wenn j= jzj k ^ jxj > jzj
(viii) Fur alle1 f 2 D' gilt: I (II) gewinnt in ( f ; ) (im Spiel A~D ),
wenn jzj k und I (II) gewinnt in ( f ; [ XXjzj ]) im Spiel A~D'
(ix) I gewinnt in ( s ; ), wenn j= jzj k ^ jxj jzj + 1
(x) II gewinnt in ( s ; ), wenn j= jzj k ^ jxj > jzj + 1
(xi) II gewinnt in ( B ; ), wenn j= jzj k ^ jxj jzj + 1 jyj
i
i
i
i
i
i
i
i
i
i
i
i
i
Der U bersichtlichkeit halber ist fur einige Felder von D in der Abbildung auf dem
Extrablatt je eine Ungleichung angegeben. Der Hilfssatz sagt dann (bis auf Endlichkeitsbedingungen): I gewinnt auf einem Feld, wenn die zugehorige Ungleichung
erfullt ist, II gewinnt, wenn sie nicht erfullt ist.
Beweis: Wir zeigen alle Behauptungen simultan durch Induktion uber k. Fur
k = 0 ist nichts zu zeigen, da X0 = ;. Wir nehmen nun an, da die Behauptungen
fur k 1 schon bewiesen sind und zeigen sie der Reihe nach fur k. Hierzu geben wir
jeweils die behauptete Gewinnstrategie in Form einer Anleitung wieder.
(i) Falls jxj = 1 ist, ziehe nach D. Du bist auf s0 wieder am Zug und gewinnst
gema Hilfssatz 2. Falls jxj > 1 ist, ziehe nach B , wahle z mit jzj = jxj 1
und gewinne gema (xi) fur k 1.
i
i
i
(ii) Fall 1 Die Gegnerin zieht nach A :
i
Gewinne gema (i)
Fall 2 Die Gegnerin zieht nach F :
Ziehe nach D und wahle x mit jxj = 1. Das geht, denn ware X1 = ; so
ware auch X1 = ; und jxj k unmoglich. Du bist auf s0 wieder am
Zug und gewinnst gema Hilfssatz 2.
Fall 3 Die Gegnerin zieht nach E und wahlt z mit jxj jzj:
Ziehe nach G (dann ist jxj jyj), du bist auf A wieder am Zug und
gewinnst gema (i)
Fall 4 Die Gegnerin zieht nach E und wahlt z mit jxj > jzj:
Ziehe nach H, wahle x mit jxj = jzj + 1. ( jzj kann nicht maximal sein,
denn sonst ware jxj > jzj nicht moglich gewesen). Dann ist auf B die
Gegnerin am Zug, jxj = jzj + 1 = jyj und du gewinnst gema (xi) fur
k 1 (jzj k 1, denn nach Voraussetzung dieses Falles wurde im Zug
nach E z mit jzj < jxj k gewahlt).
i
i
i
i
i
i
i
i
i
i
(iii) Folgt aus (ii).
(iv) Fall 1 jzj + 1 > jyj (also jyj jzj):
Ziehe nach C und gewinne gema (ii)
Fall 2 jzj + 1 jyj und jxj > jzj + 1:
Da nach Voraussetzung jyj k ist, ist jzj k 1. Ziehe nach s und
gewinne gema (x) fur k 1.
i
i
1
Fast: Alle auer Exit und denen, die am Ende eines der abgeanderten Pfeile liegen
37
(v) Da jxj > jyj ist, ist jxj mindestens 2. Zieht die Gegnerin nach D , so ist sie
auf s0 wieder am Zug und du gewinnst gema Hilfssatz 2. Zieht sie nach B ,
gewinne gema (iv) (jxj jzj + 1 jyj geht nicht wegen jxj > jyj!)
(vi) und (vii) Folgen aus (v)
(viii) Sei Str eine Gewinnstrategie fur I (II) fur ( f ; [ XXjzj ]) im Spiel A~D' . Wir
geben eine Gewinnstrategie fur I (II) fur ( f ; ) im Spiel A~D an:
i
i
i
i
i
Verfahre innerhalb von D' stets gema Str. Ziehst du dabei einen Pfeil, der
in D' mit \X r" beschriftet war, so gilt jrj jzj, sonst ware Str keine Gewinnstrategie gewesen. Da in D' dieser Pfeil mit \x := r" beschriftet ist, gilt
nach diesem Zug jxj jzj. Du bist auf e wieder am Zug und gewinnst gema
(iii).
Zieht die Gegnerin einen abgeanderten Pfeil, so gilt nach diesem Zug: jxj > jzj,
sonst ware Str ebenfalls keine Gewinnstrategie gewesen. Die Gegnerin ist dann
auf e wieder am Zug und du gewinnst gema (vii).
(ix) Wegen jxj jzj + 1 gilt (x) 2 F' (Xjzj), also (A; [ XXjzj ]) j= ' und damit
I gewinnt (A; [ XXjzj ])D' . Mit (viii) fur f = s0 folgt die Behauptung.
i
i
i
i
(x) Analog zu (ix), die Remisfreiheit von D' ausnutzend
(xi) Falls die Gegnerin nach s zieht, gewinne gema (ix). Falls sie nach C zieht,
ist dann jzj + 1 jxj, also jxj > jzj und du gewinnst gema (vi).
i
i
2
Hilfssatz 4 I gewinnt ( C ; ) wenn dort gilt: jxj = 1
Beweis: Wir geben eine Gewinnstrategie fur I an:
Fall 1 X1 = ;:
Ziehe nach F . Die Gegnerin ist auf s0 wieder am Zug. Unabhangig von der
Wahl von x ist dort jxj = 1 und du gewinnst gema Hilfssatz 2
Fall 2 X1 = Xm =6 Xm 1:
Ziehe nach E und wahle z mit jzj = m (also maximal).
Fall 2.1 Die Gegnerin zieht nach H und wahlt x mit jxj < 1:
Du bist auf B wieder am Zug. Dort ist dann jyj = jxj < 1 und deshalb
jzj + 1 > jyj, weil jzj maximal war. Gewinne gema Hilfssatz 3(iv).
Fall 2.2 Die Gegnerin zieht nach H und wahlt x mit jxj = 1:
i
i
i
i
i
i
i
Du bist auf B wieder am Zug. Ziehe2 nach s und gewinne gema
Hilfssatz 3(x).
Fall 2.3 Die Gegnerin zieht nach G :
Danach gilt jyj = m und jxj = 1, also jxj > jyj Die Gegnerin ist auf A
wieder am Zug, und du gewinnst gema Hilfssatz 3(v)
i
i
i
i
2
2
Hier ist deshalb ein weiterer Zug notwendig, weil Hilfssatz 3(iv) ungeschickt formuliert ist.
38
Hilfssatz 5 Fur alle3 f 2 D' und alle mit j= jzj = 1 gilt:
I (II) gewinnt ( f ; ) (in A~[ XX1 ]D' ) ) I (II) gewinnt ( f ; ) in A~D
Beweis: Der Beweis verlauft analog zu dem von Hilfssatz 3(viii), was uns nicht
daran hindert, ihn nochmal hinzuschreiben.4 Sei Str eine Gewinnstrategie fur I (II)
fur ( f ; [ XX1 ]) im Spiel A~D' .
Wir geben eine Gewinnstrategie fur I (II) fur ( f ; ) im Spiel A~D an:
Verfahre innerhalb von D' stets gema Str. Ziehst du dabei einen der abgeanderten
Pfeile, so gilt in der Stellung nach diesem Zug jxj < 1, sonst ware Str keine Gewinnstrategie gewesen. Du bist auf e wieder am Zug und gewinnst gema Hilfssatz
3(iii). (Nach Voraussetzung war jzj = 1).
Zieht die Gegnerin einen abgeanderten Pfeil, so gilt in der Stellung nach diesem Zug:
jxj = 1, sonst ware Str ebenfalls keine Gewinnstrategie gewesen. Die Gegnerin ist
i
i
i
i
i
i
dann auf e wieder am Zug, zieht nach C und du gewinnst gema Hilfsatz 4 2
Wir zeigen jetzt, da D remisfrei ist, indem wir die Ergebnisse der Hilfssatze zusammentragen.
( C ; ) ist Gewinnstellung, wenn jxj > jzj (Hilfssatz 3(vi)) oder wenn jxj = 1 (Hilfssatz 4). Andernfalls ist ( C ; ) Verluststellung (Hilfssatz 3(ii)), also jedenfalls keine
Remisstellung.
Fur f in D' ist ( f ; ) keine Remisstellung (wenn jzj endlich nach Hilfssatz 3(viii)
und wenn jzj unendlich nach Hilfssatz 5. Beachte zu beidem: D' ist remisfrei!)).
Fur f in D'0 ist ( f ; ) ebenfalls keine Remisstellung (Hilfssatz 1).
Da von einer beliebigen Stellung aus nach spatestens 4 Halbzugen eine der vorgenannten Stellungen erreicht ist, ist D remisfrei.
i
i
i
i
i
i
i
i
Wer gewinnt nun das Spiel insgesamt (d.h. in der Startstellung)?
Nach dem ersten Halbzug ist die Stellung ( C ; [ xt ; yt ]), also jxj = jzj = jtj. Wenn
nun A~(t) 2 X1 , also jtj endlich, ist dies eine Verluststellung (Hilssatz 3(ii)) also die Startstellung eine Gewinnstellung. Andernfalls verhalt sich dies umgekehrt
(Hilfssatz 4). Wir haben also:
i
I gewinnt A~D , (t) 2 X1
3
4
(, A~ j= )
2
Wie vorher: Alle auer Exit und denen, die am Ende eines der abgeanderten Pfeile liegen
Redundanz ist gut. Redundanz ist gut. Redundanz ist gut.
Kapitel 8
Normalformen fur IFP
8.1 Vollstandigkeit von GAME
Mit dem Hauptsatz haben wir gezeigt, da GAME hart fur IFP bezuglich quantorenfreier Reduktion ist (= Kor 36). Wir zeigen nun, da GAME sogar in LFP
denierbar ist.
Satz 51 Fur alle s -Strukturen S gilt:
S 2 GAME , S j= [LFPXux
(u =:: x ^ 9vy(Zxy ^ v =
6 : y ^ Xvy))
_ (u =6 x ^ 8y(Zxy ! Xyy))
]ss
Beweis: Sei S fest gewahlt und ' := '(X; ux) der 1.Stufe-Anteil der Formel im
Satz. Man zeigt leicht durch Induktion uber k, da
falls k gerade ist, gilt:
I gewinnt (S; Z; a) in k Halbzugen , aa 2 F'k (;)
falls b 6= a ist und k ungerade, gilt:
II gewinnt (S; Z; a) in k Halbzugen , ba 2 F'k (;)
(Idee: In den ungeraden Iterationsstufen kommen nur Stellungen x hinzu, in denen
ich gewinne, wenn ich nicht dran bin. Diese werden mit u 6= x markiert. In den
geraden Iterationsstufen kommen nur Stellungen x hinzu, in denen ich gewinne,
wenn ich dran bin. Letztere werden mit u = x markiert.)
2
Es folgt ss 2 F'1 (;) , I gewinnt S
GAME ist also denierbar in LFP. Insgesamt haben wir also:
Satz 52 GAME ist vollstandig fur IFP bezuglich quantorenfreier Reduktion.
2
8.2 Skolemsche Normalform, IFP=LFP
Wir nutzen nun den in Kapitel 3 besprochenen Zusammenhang zwischen vollstandigen Problemen und Normalformen:
Satz 53 (Skolemsche Normalform fur IFP [Dah87])
Jede IFP-Formel ist aquivalent zu einer Formel der Gestalt
[LFPX x ']t mit einer 2 -denierbaren 1.Stufe-Formel '.
39
40
Beweis: Sei die Formel aus Satz 51. Diese deniert ein vollstandiges Problem
fur IFP bezuglich quantorenfreier Reduktion. Nach Satz 26 ist dann
f j ist quantorenfreie U bersetzung von s g eine Normalform fur IFP. Der 1.StufeAnteil von und damit auch der von ist 2 -denierbar.1 Also haben alle die geforderte Gestalt
2
Bemerkung: Die U bersetzung im obigen Beweis wird letztlich durch den Hauptsatz geliefert. Verwendet man den Zusatz, so kann man in der Normalform t = d~
erreichen (zur Variable d siehe auch Abschnitt 1.6). Obwohl d dann frei in der Formel [LFPX x ']d~ vorkommt, hangt diese nicht von der Belegung von d ab. Wer
aus weltanschaulichen oder denitionstechnischen Grunden keine unquantizierten
Variablen duldet, kann d auch mit 8, 9 oder einem anderen Quantor eigener Wahl
abquantizieren.
Das hier gesagte gilt auch fur alle weiteren Normalformen in diesem Aufsatz.
Aus Satz 53 folgt unmittelbar:
Satz 54 ([GS86]) IFP=LFP 2
8.3 Beschrankte Skolemsche Normalform
Nach dem selben Schema erhalten wir noch weitere Normalformen fur IFP.
Satz 55 Fur alle s -Strukturen S gilt:
(a) I gewinnt S , [LFPXx 9y(Zxy ^ 8z(Zyz ! Xz))]s
(b) II gewinnt S , [LFPXx 8y(Zxy ! 9z(Zyz ^ Xz))]s
Beide Teile des Satzes sind leicht einzusehen. Auerdem werden wir in Abschnitt
9.4 einen Beweis nachliefern.
Satz 56 (Beschrankte Skolemsche Normalform fur IFP [Gro94]) Jede IFP-
Formel ist aquivalent zu einer Formel der Gestalt
(a) [LFPX x 9y8z(X z _ '(x; y; z))]t
und einer Formel der Gestalt
(b) [LFPX x '0 (x) _ 8y9z(X z ^ '(x; y; z))]t,
wobei '(x; y; z) (und '0 (x)) jeweils eine quantorenfreie Formel ist, in der X nicht
vorkommt.
Beweis:
zu (a) Sei die Formel aus Satz 55(a). Zxy ^ 8z(Zyz ! Xz) ist aquivalent zu
8z (Xz _ (Zxy ^ :Zyz )), unter der Voraussetzung, da es ein z gibt mit :Xz . Dies
aber ist in jeder Iterationsstufe von X der Fall, denn sonst waren alle Stellungen
Gewinnstellungen (sagt Satz 55(a)). Also ist aquivalent zu
~ := [LFPXx 9y8z (Xz _ (Zxy ^ :Zyz ))]s
Damit ist ~ eine Denition von GAME . Nach Satz 26 sind die Formeln ~ dann
eine Normalform fur IFP. Sie haben die geforderte Gestalt.
zu (b) Der Beweis ist sozusagen dual zu dem von (a), mit einer kleinen Zusatzkomplikation. Sei diesmal die Formel aus Satz 55(b). Zxy ! 9z (Zyz ^ Xz ) ist
aquivalent zu 9z (Xz ^ (Zxy ! Zyz )), unter der Voraussetzung, da es bereits ein
1
Sogar eine Boolesche Kombination von 1 -Formeln, falls das jemand interessiert.
41
z gibt mit Xz. Dies ist argerlicherweise fur X0 = ; nicht der Fall. Deshalb mussen
wir uns kunstlich einen Induktionsanfang verschaen. ist aquvivalent zu
~ := [LFPXux u =
6 : x _ 8y9wz (Xwz ^ (Zxy ! Zyz ^ w =: z ))]ss
Sei nun 2 IFP gegeben. Dann liefert uns der Hauptsatz fur : eine remisfreie
quantorenfreie U bersetzung von s mit
A~ j= : , I gewinnt A~ Da remisfrei ist, gilt auch
A~ j= , II gewinnt A~
Wegen ~ =jj= und Satz 55(b) haben wir insgesamt:
A~ j= , II gewinnt A~ , A~ j= ~ , A~ j= ~
2
Also ist ~ aquvivalent zu . ~ hat die geforderte Gestalt.
Bemerkung 57 Aus Teil (a) der beschrankten Skolemschen Normalform bekommt
man auch leicht wieder die Vollstandigkeit von GAME bezuglich quantorenfreier
Reduktion.
Fur das Diagramm
Dsko :=
6'(x; y; z)!
z? j
-
Startx := t
j
j
-
6
j
y? -
j
j
j
x := z
gilt:
I gewinnt A~Dsko , A~ j= [LFPX x 8y9z(X z _ '(x; y; z))]t
Grohe beweist in [Gro94] die beschrankte Skolemsche Normalform rein auf Formelbasis. Zusammen mit dem Beweis in Kapitel 6 ergibt sich dadurch eine weitere
Moglichkeit unseren Hauptsatz zu beweisen.
42
Kapitel 9
Negative PFP-Fragmente
Grohe betrachtet in [Gro94] unter anderem Formeln der Gestalt
[FPX x '0 _ 9y1 2 X : : : 9yl 2 X 9z1 2= X : : : 9zm 2= X ' ]t
mit quantorenfreien Formeln '0 und ', in denen X nicht vorkommt. 9v2 X' ist hierbei eine Abkurzung fur 9v(X v ^ ') und 9v2= X' eine Abkurzung fur
9v(:X v ^ ').
Diese Formeln sind im allgemeinen Fall (d.h l und m unbeschrankt) eine Normalform
fur PFP. Beschrankt man l und m durch konkrete Zahlenwerte, so erhalt man
verschiedene interessante Fragmente von PFP.
Denition 58 (PFPNF(l,m)) Fur alle l; m 2 IN ist eine PFPNF(l,m)-Formel,
wenn sie die Gestalt
[FPX x '0 _ 9y1 2 X : : : 9yl0 2 X 9z1 2= X : : : 9zm0 2= X ' ]t
hat, mit l0 l; m0 m und quantorenfreien Formeln '0 und '.
PFPNF(l,m) ist die hierdurch denierte Sublogik von PFP.
9.1 Denition
Denition 59 (PFP(l,m)) Fur alle l; m 2 IN ist PFP(l,m) die durch folgenden
Kalkul denierte Sublogik von PFP:
'
';
' wenn ' Atom; :' ; ('^ ) ;
wenn l0 l; m0 m und X
'0 ;'
[FPX x '0 _9y1 2X:::9yl0 2X 9z1 2=X:::9zm0 2=X ' ]t, nicht frei in '0 , '
Die Logik PFP(l,m) ist also die stratizierte Variante von PFPNF(l,m).
9.2 Klassizierung
.
Fur jeden Wert von l und m ist PFP(l,m) bzw. PFPNF(l,m) genauso ausdrucksstark
wie eine wohlbekannte Logik:
Pl PPm 0
0 QF
1
PFPNF(l,m) = 1 9TC LFP
PFP
2 9LFP PFP
PFP(l,m) =
43
Pl PPm 0
0 QF
1
LFP
1 TC PFP
2 SFP PFP
44
Hierbei ist TC die Logik mit einem Operator fur die transitive Hulle einer denierbaren 2k-stelligen Relation, 9TC deren existentielles Fragment, 9LFP das existentielle
Fragment von LFP und SFP die stratizierte Variante von 9LFP. Wir wollen diese
Logiken nicht denieren, da sie hier nicht Gegenstand der Diskussion sind.
Alle Falle mit l > 0 sind in [Gro94] abgehandelt. PFPNF(0,0)=PFP(0,0)=QF ist
trivial. Es bleibt also zu zeigen, da PFPNF(0,m)=PFP(0,m)=LFP fur alle m 1.
9.3 negPFP
Zunachst zeigen wir PFP(0,m) LFP. Hierzu denieren wir eine Logik, die oberhalb
aller PFP(0,m) liegt.
Denition 60 (negPFP) negPFP ist die Sublogik von PFP, die durch folgenden
Kalkul gegeben ist:
' ';
'
' wenn ' Atom; :' ; ('^ ) ; 9x' ;
' n , wenn ' negativ in X ist und X nicht frei im Geltungsbereich eines
Fixpunktoperators innerhalb von ' vorkommt
[FPX nx '] t
.
In negPFP wirken Fixpunktoperatoren nur auf Formeln die negativ und damit
antimonoton sind. Deshalb untersuchen wir jetzt antimonotone Abbildungen.
Satz 61 Sei F : Pot(An ) ! Pot(An ) antimonoton. Dann gilt
(i) F 2 ist monoton
(ii) (F 2k (;))k2IN ist eine aufsteigende Folge. Ihr Grenzwert ist lfp(F 2).
(iii) (F 2k (An))k2IN ist eine absteigende Folge. Ihr Grenzwert ist gfp(F 2).
(iv) (F 2k+1 (;))k2IN ist eine absteigende Folge. Ihr Grenzwert ist gfp(F 2 ).
(v) F 1(;) existiert , lfp(F 2) = gfp(F 2)
(vi) Wenn F 1(;) existiert, gilt fur alle R An :
F 1 (R) existiert und F 1 (R) = F 1 (;)
Beweis:
(i) klar.
(ii) und (iii) Siehe Satz 5, Denition 6.
(iv) Aus ; F (An) folgt An F (;) F 2(An ). Durch Iteration erhalten wir
allgemein F 2k (An ) F 2k+1 (;) F 2k+2 (An ). Mit (iii) folgt die Behauptung.
(v) folgt aus (ii) und (iv).
(vi) Sei F 1(;) = F 2m(;) der Fixpunkt von F . Aus ; F (R) F (;) erhalten wir
dann fur alle k m: F 1 (;) = F 2k (;) F 2k+1 (R) F 2k+1 (;) = F 1 (;).
2
Denition 62 ('2 (X; x)) Sei '(X; x) eine PFP-Formel und die Stelligkeit von X
gleich der Lange von x. Dann ist '2 (X; x) die Formel, die man erhalt, wenn man
in '(X; x) alle Subformeln der Form X r durch '(X; r) ersetzt.
45
Fur Freunde und Bekannte der Notation mit dem Unterstrich: '2 (X; x) = '('(X; ); x).
Folgende Eigenschaften der Formel '2 (X; x) sind leicht zu sehen:
Satz 63 Sei ' := '(X; x) eine PFP-Formel und die Stelligkeit von X gleich der
Lange von x. Dann gilt:
(i) F'2 = F'2
(ii) ' ist negativ in X ) '2 ist positiv in X
(iii) ' 2 LFP ) '2 2 LFP
2
Satz 64 negPFP LFP
Beweis: Es genugt zu zeigen, da jede Formel [FPX x '(X; x)]t aquivalent zu
einer LFP-Formel ist, wenn ' := '(X; x) eine in X negative LFP-Formel ist. (Dann
konnen wir in einer gegebenen negPFP-Formel von innen nach auen nacheinander
alle Fixpunktoperatoren durch LFP-Formeln ersetzen).
Nach Satz 15 ist ' antimonoton, weil negativ in X . Nach Satz 61(v) existiert F'1
genau dann, wenn lfp(F'2 ) = gfp(F'2 ). So das der Fall ist, gilt F'1 = lfp(F'2 ).
Insgesamt ist also [FPX x '(X; x)]t aquivalent zur Formel
8v [LFPX x '2 (X; x)]v $ [GFPX x '2 (X; x)]v ^ [LFPX x '2 (X; x)]t
Die Fixpunktoperatoren in obiger Formel sind tatsachlich LFP-Operatoren, da nach
Satz 63 '2 eine LFP-Formel ist und positiv in X . Zur Denition des GFP-Operators
siehe Denition 17 und Satz 18.
2
9.4 PFPNF(0,1)
Um die Logiken PFPNF(0,m) und PFP(0,m) nach unten abzuschatzen zeigen wir,
da bereits PFPNF(0,1) IFP.
Satz 65 Sei ' := '(X; x) := 9y(Zxy ^:Xy). Dann gilt fur alle Spiele S = (S; Z; s)
und alle a 2 S :
(i) Falls k gerade: a 2 F';k S (;) , I gewinnt (S; Z; a) in k Halbzugen
Falls k ungerade: a 2 F';k S (;) , II gewinnt (S; Z; a) nicht in k Halbzugen
(ii) a 2 lfp(F';2 S ) , a ist Gewinnstellung von S
(iii) a 2 gfp(F';2 S ) , a ist nicht Verluststellung von S
(iv) Der Fixpunkt von F';S existiert genau dann, wenn S remisfrei ist. In
diesem Fall ist er gleich der Menge der Gewinnstellungen von S .
Beweis:
(i) Sieht man leicht durch Induktion uber k.
(ii) ' ist antimonoton, weil negativ in X. Nach Satz 61(ii) ist lfp(F';2 S ) der Grenzwert der aufsteigenden Folge (F';2kS (;))k2IN . Nach (i) ist dies die Menge der
Gewinnstellungen von S .
(iii) Analog mit Satz 61(iv).
46
(iv) ' ist antimonoton, weil negativ in X. Nach Satz 61(v) existiert der Fixpunkt
von F';S genau dann, wenn lfp(F';2 S ) = gfp(F';2 S ). Mit (ii) und (iii) ist dies
genau dann der Fall, wenn fur alle a 2 S gilt: a ist Gewinnstellung , a ist
nicht Verluststellung, also wenn S remisfrei ist.
2
Wir tragen nun den in Abschnitt 8.3 angekundigten Beweis von Satz 55 nach:
Beweis von Satz 55: Sei '(X; x) := 9y(Zxy ^ :Xy), wie im vorigen Satz. Dann
gilt nach (ii) und (iii):
(a) I gewinnt S , [LFPXx '2(X; x)]s
(b) II gewinnt S , :[GFPXx '2(X; x)]s
Man rechnet nach, da
[LFPXx '2 (X; x)]s = [LFPXx 9y(Zxy ^ 8z (Zyz ! Xz ))]s
und
:[GFPXx '2 (X; x)]s = [LFPXx 8y(Zxy ! 9z (Zyz ^ Xz ))]s.
Dies sind erfreulicherweise die Formeln aus Satz 55.
(Zu letzterem verwende man :[GFPXx '2 (X; x)]s = [LFPXx :'2 (:X; x)]s ) 2
Denition 66 (\) \ := [FPXx 9y(:Xy ^ Zxy)]s
Satz 67 Mod(\) = GAME \ RF
Beweis: Folgt aus Satz 65(iv).
2
Satz 68 GAME \ RF ist in LFP denierbar.
Beweis: \ 2 negPFP LFP (nach Satz 64).
2

Satz 69 Jede IFP-Formel ist aquvivalent zu \ fur eine quantorenfreie Uberset-
zung von s
Beweis: Nach Korollar 37 ist Mod(\) = GAME \ RF hart fur IFP bezuglich
quantorenfreier Reduktion. Satz 26 liefert die Behauptung.
2
Es handelt sich hier nicht um eine Normalform fur IFP. Zwar sind alle IFP-Formeln
aquivalent zu einem \ , aber diese Formeln sind im Allgemeinen keine IFPFormeln. Der Iterationsprozess ist bei ihnen nur in pathologischen Fallen induktiv.
Dafur ist es eine Normalform fur negPFP, da \ 2 negPFP ist und negPFP=IFP,
wie wir gleich sehen werden.
Satz 70 IFP PFPNF(0,1)
Beweis: Dies folgt aus dem vorigen Satz, da die Formeln \ oensichtlich
PFPNF(0,1)-Formeln sind.
2
9.5 Happy End
Satz 71 LFP = IFP = PFPNF(0,m) = PFP(0,m) fur alle m 2 IN
Beweis: Mit Satz 70 und Satz 64 haben wir:
LFP = IFP PFPNF(0,1) PFPNF(0,m) PFP(0,m) negPFP LFP 2
Anhang A
Literatur
[Dah87] E.Dahlhaus. Skolem normal forms concering the least xed point. In
E.Borger (Hg) Computation Theory and Logic, 270, Lecture Notes in Computer Science, pp. 20-36. Springer-Verlag, 1987
[EF95] H.-D. Ebbinghaus und J. Flum. Finite Model Theory. Springer-Verlag, 1995
[Gro94] M. Grohe. The Structure of Fixed-Point Logics, Dissertation an der Universitat Freiburg i. Br. 1994
[GS86] Y. Gurevich und S. Shelah. Fixed point extensions of rst order logic. In
Annals of pure and applied logic, 32, pp. 265-280, 1986
[Haa94] L. Haarer. Kochen und Backen nach Grundrezepten - Neuausgabe mit
farbigen Phasenfotos. Schneider Verlag Hohengehren, 1994
[Imm82] N. Immerman, Relational Queries Computable in Polynomial Time. In
Proceedings of 14th ACM symposion on the theory of computing, pp. 147-152,
1982
[JL76] N.D. Jones und W.T.Laaser. Complete problems for deterministic polynomial time. In Theoretical Computer Science, 3, pp. 105-117, 1976
[Rei90] K.R. Reischuk. Einfuhrung in die Komplexitatstheorie. Teubner, 1990
[Var82] M. Vardi. The complexity of relational query languages. In Proceedings of
14th ACM symposion on the theory of computing, pp. 137-146, 1982
47
Index
( f ; ), 20
F 1 (R), 11
F';A~, 11
Xk , 31
A~, 7
A~[ xa ], 7
A~D , 20
A~ , 13
GAME , 16
nn c , 13
o, o, 8
, 13
RF , 17
=jj=, 8
: [ xa ], 7
=, 12
'2 (X; xn), 44
n
y), 9
'A~(x;
Mod(
'), 8
R (xn 1 ; : : : ; xn k ), 13
, 14
\ , 46
s , 15
, 7
d; d~, 8
l(a), 24
jaj, 31
s0, s , e , 31
gfp(F), 11
lfp(F), 11
antimonoton
Abbildung, 11
Formel, 12
Atom, 12
atomare Formel, 12
Beschriftung, 19
brav, 21
denierbar, 13
Diagramm, 19
entschieden
Diagramm, 21
Spiel, 17
U bersetzung von s , 17
Exitfeld, 22
Feld, 19
Figur von D, 20
Fixpunkt, 11
FO, 8
Gewinnstellung, 16
Gewinnstrategie, 16
gewinnt, 16
hart, 13
Hauptsatz, 17
IFP, 12
induktiv
Abbildung, 11
Formel, 12
Interpretation, 7
L[], 8
LFP, 12
Logik, 8
monoton
Abbildung, 11
Formel, 12
negativ, 12
negPFP, 44
Normalform, 8
Pfeil, 19
PFP(l,m), 43
PFP-Semantik, 12
PFP-Syntax, 12
PFPNF(l,m), 43
positiv, 12
QF, 8
Reduktion, 13
remisfrei
Diagramm, 21
Spiel, 17
U bersetzung von s , 17
Remisstellung, 17
Spiel, 15
Startfeld, 19
Startstellung, 15
Stellung, 15
Strategie, 15
U bersetzung, 13
Verluststellung, 16
vollstandig, 13
Zug, erlaubter, 15
i
i
i
i
48