Abschnitt 1, 1. Übungsstunde
Werbung
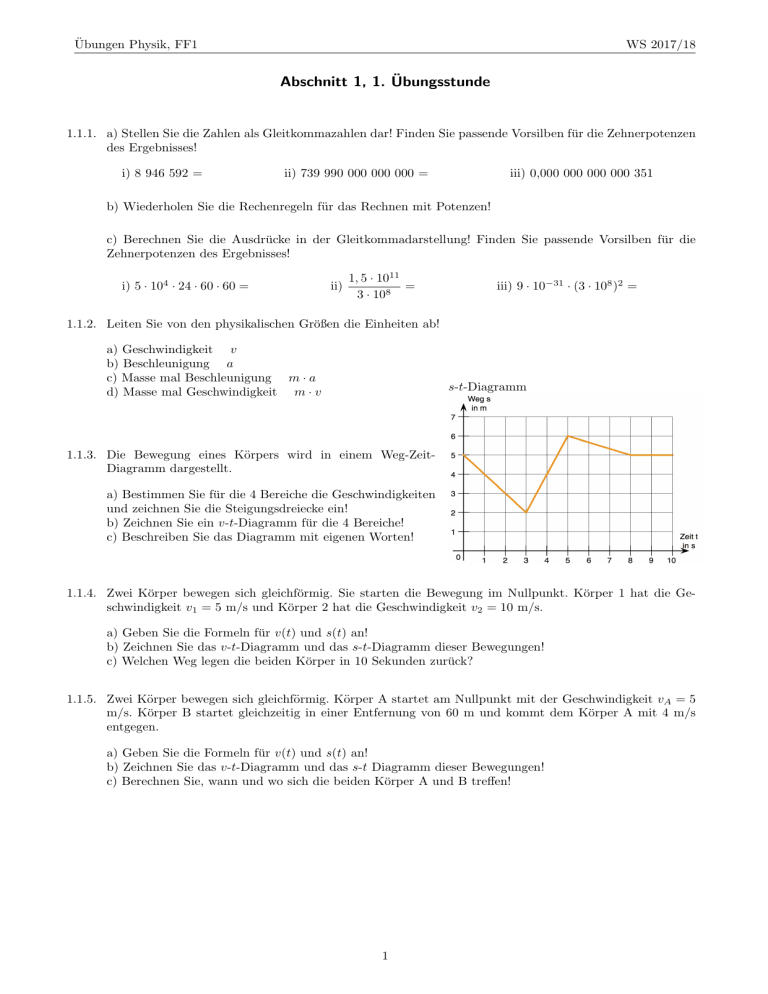
Übungen Physik, FF1 WS 2017/18 Abschnitt 1, 1. Übungsstunde 1.1.1. a) Stellen Sie die Zahlen als Gleitkommazahlen dar! Finden Sie passende Vorsilben für die Zehnerpotenzen des Ergebnisses! i) 8 946 592 = ii) 739 990 000 000 000 = iii) 0,000 000 000 000 351 b) Wiederholen Sie die Rechenregeln für das Rechnen mit Potenzen! c) Berechnen Sie die Ausdrücke in der Gleitkommadarstellung! Finden Sie passende Vorsilben für die Zehnerpotenzen des Ergebnisses! i) 5 · 104 · 24 · 60 · 60 = ii) 1, 5 · 1011 = 3 · 108 iii) 9 · 10−31 · (3 · 108 )2 = 1.1.2. Leiten Sie von den physikalischen Größen die Einheiten ab! a) Geschwindigkeit v b) Beschleunigung a c) Masse mal Beschleunigung m · a d) Masse mal Geschwindigkeit m · v s-t-Diagramm 1.1.3. Die Bewegung eines Körpers wird in einem Weg-ZeitDiagramm dargestellt. a) Bestimmen Sie für die 4 Bereiche die Geschwindigkeiten und zeichnen Sie die Steigungsdreiecke ein! b) Zeichnen Sie ein v-t-Diagramm für die 4 Bereiche! c) Beschreiben Sie das Diagramm mit eigenen Worten! 1.1.4. Zwei Körper bewegen sich gleichförmig. Sie starten die Bewegung im Nullpunkt. Körper 1 hat die Geschwindigkeit v1 = 5 m/s und Körper 2 hat die Geschwindigkeit v2 = 10 m/s. a) Geben Sie die Formeln für v(t) und s(t) an! b) Zeichnen Sie das v-t-Diagramm und das s-t-Diagramm dieser Bewegungen! c) Welchen Weg legen die beiden Körper in 10 Sekunden zurück? 1.1.5. Zwei Körper bewegen sich gleichförmig. Körper A startet am Nullpunkt mit der Geschwindigkeit vA = 5 m/s. Körper B startet gleichzeitig in einer Entfernung von 60 m und kommt dem Körper A mit 4 m/s entgegen. a) Geben Sie die Formeln für v(t) und s(t) an! b) Zeichnen Sie das v-t-Diagramm und das s-t Diagramm dieser Bewegungen! c) Berechnen Sie, wann und wo sich die beiden Körper A und B treffen! 1 Übungen Physik, FF1 WS 2017/18 1.1.6. Von zwei Radfahrern wird der zurückgelegte Weg gemessen und im Diagramm dargestellt. a) Beschreiben Sie, was die zwei Kurven darstellen und wie sich die Radfahrer bewegen! Was bedeutet der Schnittpunkt? b) Berechnen Sie die Geschwindigkeiten der 2 Radfahrer in m/s und in km/h! (Beachten Sie die Einheiten auf den Achsen!) c) Zeichnen Sie das v-t Diagramm von beiden Bewegungen! d) Bestimmen Sie die Bewegungsgleichungen s1 (t) und s2 (t) der Radfahrer! e) Berechnen Sie wann und wo sich die Radfahrer treffen! 1.1.7. Ein Auto beschleunigt gleichmäßig aus dem Stillstand mit 2 m/s2 . a) Geben Sie die Formeln für a(t), v(t) und s(t) an! b) Zeichnen Sie das a-t-Diagramm, das v-t-Diagramm und das s-t-Diagramm dieser Bewegung! c) Welchen Weg hat das Auto nach 10 Sekunden zurückgelegt? Welche Geschwindigkeit hat das Auto nach 10 Sekunden? 1.1.8. Die Bewegung eines Elektroautos wird Geschwindigkeit-Zeit-Diagramm dargestellt. in einem a) Bestimmen Sie für die 5 Bereiche die Beschleunigungen und zeichnen Sie die Steigungsdreiecke ein! b) Zeichnen Sie ein a-t-Diagramm für die 5 Bereiche! c) Ordnen Sie den 5 Bereichen folgende Begriffe zu: gleichförmige Bewegung gleichmäßig beschleunigte Bewegung ungleichmäßig beschleunigte Bewegung Stillstand d) Beschreiben Sie das Diagramm mit eigenen Worten! 1.1.9. Ein Auto hat die Geschwindigkeit 180 km/h. Es bremst gleichmäßig und kommt nach 150 m zum Stillstand. a) Geben Sie die Formeln für a(t), v(t) und s(t) an! b) Berechnen Sie die Bremsbeschleunigung und die Bremszeit! c) Zeichnen Sie das a-t-Diagramm, das v-t Diagramm und das s-t Diagramm dieser Bewegung! d) Nennen Sie die wichtigsten Merkmale der gleichförmigen Bewegung und der gleichmäßig beschleunigten Bewegung! 1.1.10. Ein Fahrzeug bescheunigt gleichmäßig aus dem Stillstand in 4 Sekunden auf 3 m/s. Diese Geschwindigkeit behält es 3 Sekunden lang, und dann beschleunigt es gleichmäßig innerhalb von 2 Sekunden auf 6 m/s. Anschließend bremst es gleichmäßig in 5 Sekunden bis zum Stillstand. a) Zeichnen Sie das v-t-Diagramm dieser Bewegung! b) Berechnen Sie für die 4 Bereiche die Beschleunigungen und zeichnen Sie das a-t-Diagramm! c) Berechnen Sie den gesamten zurückgelegten Weg! 2

