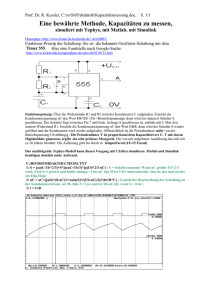
XFER mit Tephys und mit Matlab berechnet

Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 1/1
Komplexe Übertragungsfunktion
mit FFT berechnet (Tephys und Matlab)
R1
Tiefpass 5.Ordnung
2 CLC –Pi-Glieder,
hat 5 Energiespeicher,
also Tiefpass 5. Ordnung
u0
C1
i1
L1
u1 C2
i2 R2
u2
L2
fak*R1
C3
u3
Methode zum Aufstellen der DGLn von RLC-Schaltungen vgl.
http://www.home.hs-karlsruhe.de/~kero0001/aufst6/AufstDGL6hs.html
1 d=drei(fd*t+del) { d = Dreieckfunktion, Frequenz fd, Phase del }
2 u01=As0*sin(2*pi*fs*t)+ar*ja(d-sw)+DC+aD*d+ap*ja(t-t1)*ja(t2-t)
3 u0=u01+aG*glock((t-t1)/dtG) {u0 = Eingangsspannung. wahlweise sinus, periodisches Rechteck,
Dreieck, pulsförmiges Rechteck oder Glockenimpuls (Hinweis: glock(x)=exp(-x*x)}
4
5
6
7
8
9
u1=u1+((u0-u1)/R1-i1)*dt/C1 { u1 = Spannung am Kondensator C1}
i1=i1+(u1-u2)*dt/L1 { i1 = Strom durch Spule L1}
u2=u2+(i1-i2)*dt/C2 { u2 = Spannung am Kondensator C2 }
i2=i2+(u2-R2*i2-u3)*dt/L3 { i2 = Strom durch Spuile L2 }
u3=u3+(i2-u3/(fak*R1))*dt/C3 {u3 = Spannung am Kondenstor C3}
t=t+dt {}
Datei RCLK_41.txt, 2 CLC-Pi-Glieder, also Tiefpass 5. Ordnung.
Schaltung: u0 über R1 mit C1 an Erde. C1 über L2 mit C2 (C2 ebenfalls an Erde). C2 mit
L2 an C3. C3 ebenfalls an Erde. Parallel C3 liegt Widerstand fak*R1 (fak=1)
Anschließend die Berechnung in Matlab, ist dem Tephys-Algorithmus „nachempfunden“
Wichtig: Ausgabevektoren groß (U0, U1, U2,U3) innerhalb der Berechnungsschleife klein (u0,u1,u2,u3)
function [t,U0,U3]=RCLK32(dt,tmax,Bild, aUp,t1,dt1,R1, C1,RL1,L1, C2,RL2,L2,C3,fakt, F, N)
%function [t,U0,U3]=RCLK32(dt,tmax,Bild,aUp,t1,dt1, R1, C1 ,RL1,L1, C2,RL2, L2,C3, fakt,N)
% mit Anzahl Speicherpunkte = 2048 --> Anpassen tmax an dt, im Spekrum N Punkte darstellen
%
nur jeder nsp-te Rechenwert wird gespeichert
%
% gute XFer:
RCLK32(0.01,150, 1, 1 ,1 ,0.5,0.8,1, 0, 1, 2, 0, 1, 1, 1,'g',100);
% mit scharfen Res: RCLK32(0.01,150, 1, 1 ,1 ,0.5, 20,1, 0, 1, 2, 0, 1, 1, 1,'g',100);
%
also R1 =20
% R. Kessler Januar 2005
% Tiepass 5. Ordnung, 2 CLC-Pi-Glieder, vgl Tephysdatei RCLk_41.txt
format compact; % verhindert unnötige Leezeilen
tmaxalt=tmax; Nmax=2048;
nsp=floor(tmaxalt/(Nmax*dt)) % nur jeder nsp-te Rechenwert wird gespeichert
tmax=nsp*Nmax*dt % tmax wird angepasst
t=0:dt:tmax-dt;
Lt=length(t)
% Initialisierungen Ausgabevektoren:
T=zeros(0,Nmax); U0=T; U1=T; U2=T; U3=T;
u1=0; u2=0; u3=0; i1=0; i2=0; % Anfangswerte
dn=1; n=1; % Zähler für Speichern
if F=='g' x=((t-t1)/dt1) .^2; U0q=aUp*exp(-x );end; % Glockeninpuls
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 2/2
for k=1:length(t);
if F=='g' u0=U0q(k); % Glockenimpuls
else
u0=aUp* (t(k)>t1) * (t1+dt1>t(k)); % RechteckPuls im Bereich t1...t2
end;
if dn==1 % Ausgabevektoren füllen:
T(n)=t(k); U0(n)=u0; U1(n)=u1; U2(n)=u2; U3(n) = u3;
end;
u1=u1+( (u0-u1)/R1-i1)*dt/C1;
i1=i1+(u1-u2-RL1*i1)*dt/L1;
u2=u2+(i1-i2)*dt/C2;
i2=i2+( u2-u3-RL2*i2 )*dt/L2;
u3=u3+( i2-u3/(fakt*R1) )*dt/C3;
dn=dn+1; % Speicherzähler
if dn > nsp dn=1; n=n+1; end; % Speicherzähler aktualisieren
end; % for k=1...
figure(Bild); plot(T,U0/10, T,U3); grid on; %zoom on;
xlabel('Zeit/sec'); ylabel('U0,U3');
fftu3=fft(U3,Nmax); fftu0= fft(U0,Nmax); % Spektren von U3 und U0
xfer=fftu3 ./ fftu0; % Transferfunktion ("xfer")
% beachte die gliedweise Division der Spektren von U3 und U0:
xfer1=xfer(1:Nmax/2); % Transferfunktion nur bis Nmax/2,
% denn ab Nmax/2 wiederholt sich das Spektrum
fftu01=fftu0(1:Nmax/2); % Spektrum U0
nur bis Nmax/2
Lf=length(xfer) % sollte 2048 ergeben
Lf1=length(xfer1);
LT=length(T)
df=1/tmax; % df= Frequenzschrittweite
f=0:df:Lf1*df-df;
Lf1=length(f);
figure(Bild+1);
% Spektrum, aber nur N Frequenzpunkte werden gezeichnet
plot(f(1:N),abs(xfer1(1:N)),f(1:N),-0.2+angle(xfer1(1:N))*0.18/pi);
grid on;
xlabel('Freq/Hz'); ylabel('abs(xfer) und angle(xfer) -0.2');
figure(Bild+2);
plot(f,abs(fftu01)); % Spektrum von U0 bis Nmax/2
grid on; xlabel('Freq/Hz'); ylabel('abs(fftu01)');
% Als Eingabe-Erleichterung:
disp(' RCLK32(dt,tmax,Bild,aUp,t1,dt1, R1, C1 ,RL1,L1, C2,RL2, L2,C3, fakt, N) ');
Anschließend zunächst drei Aufrufe mit Matlab, dann drei Aufrufe mit Tephys.
Dabei Widerstand R1 variiert: R=0.2, R1=20, R1=0.8
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 3/3
0.3
0.25
0.2
R C L K 3 2 (0 . 0 1 , 1 5 0 , 1 , 1 , 5 , 1 . 1 , 0 . 2 , 1 , 0 , 1 , 2 ,
0,
1 , 1 , 1 , 'g ', 1 0 0 );
U 0,U 3
0.15
0.1
0.05
0
-0 . 0 5
0
50
100
150
Ze it / s e c
0.5
0.4
abs (x fer)und angle(x fer) -0.2
0.3
0.2
R C LK 32(0.01,150, 1, 1 ,5 ,1.1,0.2,1, 0, 1, 2,
0,
1, 1, 1,'g',100);
0.1
0
-0.1
-0.2
-0.3
-0.4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
F req/H z
Aufruf für die beiden obigen Bilder war:
RCLK32(0.01,150, 1, 1 ,5 ,1.1,0.2,1, 0, 1, 2,
0,
1, 1, 1,'g',100);
RCLK32(dt,tmax,Bild,aUp,t1,dt1, R1, C1 ,RL1,L1, C2,RL2, L2,C3, fakt, N)
Erkenntnis: Widerstand R1=0.2 ist zu klein, drum Resonanzstelle in Übertragungsfunktion u3/u0
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 4/4
0.1
0.08
RCLK32(0.01,150, 4, 1 ,5 ,1.1,20,1, 0, 1, 2,
0,
1, 1, 1,'g',100);
0.06
U0,U3
0.04
0.02
0
-0.02
-0.04
0
50
100
150
Zeit/sec
0.5
0.4
abs (x fer)und angle(x fer) -0.2
0.3
0.2
0.1
0
RCLK 32(0.01,150, 4, 1 ,5 ,1.1,20,1, 0, 1, 2,
0,
1, 1, 1,'g',100);
-0.1
-0.2
-0.3
-0.4
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
F req/Hz
Aufruf für die beiden obigen Bilder war:
RCLK32(0.01,150, 4, 1 ,5 ,1.1,20,1, 0, 1, 2,
0,
1, 1, 1,'g',100); also R1=20 Ohm
RCLK32(dt,tmax,Bild,aUp,t1,dt1, R1, C1 ,RL1,L1, C2,RL2, L2,C3, fakt, N)
Erkenntnis: Widerstand R1=20 ist zu groß, drum 2 Resonanzstellen in Übertragungsfunktion u3/u0
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 5/5
0 .4
0 .3 5
0 .3
R C L K 3 2 (0 . 0 1 , 1 5 0 , 7 ,
1 ,5 ,1 .1 , 0 .8 , 1 ,
0,
1,
2,
0,
1,
1 , 1 , 'g ', 1 0 0 ) ;
0 .2 5
U 0 ,U 3
0 .2
0 .1 5
0 .1
0 .0 5
0
-0 . 0 5
-0 . 1
0
50
100
150
Z e it / s e c
0 .6
a b s ( x fe r ) u n d a n g l e ( x fe r ) - 0 . 2
0 .5
0 .4
0 .3
0 .2
0 .1
0
R C L K 3 2 (0 . 0 1 , 1 5 0 , 7 ,
1 ,5 ,1 .1 , 0 .8 , 1 ,
0,
1,
2,
0,
1,
1 , 1 , 'g ', 1 0 0 ) ;
-0 . 1
-0 . 2
-0 . 3
-0 . 4
0
0 .1
0 .2
0 .3
0 .4
0 .5
0 .6
0 .7
F re q / H z
Aufruf für die beiden obigen Bilder war:
RCLK32(0.01,150, 7, 1 ,5 ,1.1, 0.8 , 1, 0, 1, 2,
0,
1, 1, 1,'g',100);
RCLK32(dt,tmax,Bild,aUp,t1,dt1, R1, C1 ,RL1,L1, C2,RL2, L2,C3, fakt, N)
Erkenntnis: Widerstand R1=0.8 ist optimal, drum glatter Verlauf (ohne Resonanzstellen) in
Übertragungsfunktion u3/u0
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 6/6
Bild 1 und Bild F1 mit R1=0.2, also zu klein, drum XFER u3/u0 NICHT optimal, hat eine Resonanzfrequenz
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 7/7
Bild 2 und Bild F2 mit R1=20, also zu groß, drum XFER u3/u0 NICHT optimal, hat zwei Resonanzfrequenzen
Bild 3 und Bild F3 mit R1=0.8, das ist optimal, denn XFER u3/u0 optimal glatt, ohne Resonanzfrequenz
Prof. Dr. R. Kessler, FH-Karlsruhe, C:\ro\Si05\f4ueb\F4UEB\XFERer_Tphys_Matlab_2.doc,
Seite 8/8
Frequenztabellen bei R1 groß (R1= 20)
C1=1, C2=2, C3=1, L1=1, L2=1
Eingabe Referenzposition: 1
Die Positionen steigend oder fallend numeriert? (s/f)
Zu grunde liegende FreqTabellen: rclk.*
-------------------------------------------FreqNr:
1 :
-----------Freq
U
Wink(grd) U/Uref Pos Form 1: 0.16 Hz
0.160
1.0000
0.00
1.000 1
|-----+
0.160
0.0014
-40.48
0.001 2
+
0.160
1.0016
-178.70 -1.002 3
+------|
FreqNr:
2 :
-----------Freq
U
Wink(grd) U/Uref Pos Form 2: 0.22 Hz
0.223
1.0000
0.00
1.000 1
|-----+
0.223
1.0037
178.82 -1.004 2
+-----|
0.223
1.0052
1.63
1.005 3
|-----=> Frequenzverhältnis f2/f1 = 0.223214 / 0.160435 = 1.39313
Theoretische Deutung der Frequenzen bei R1 hochohmig:
Tiefe Frequenz f1; u1 gegenphasig zu u2, u2=0, entspricht LC-Kreis mit L=1, C=C1=1, => f1=1/(2*pi*sqrt(1*1) = 1/(2*pi)
Hohe Frequenz f2: u1 und u3 gleichphasig, u2 gegenphasig. Entspricht Schwingkreis mit L, C1 in Reihe mit C2/2,
also Gesamtes C= 1 in Reihe mit 1, also C=1/2 => f2=1/(2*pi*sqrt(1*1/2) ) = sqrt(2)/(2*pi).
==> Frequenzverhältnis f2/f1 = sqrt(2) = 1.414
Wenn R1 niederohmig, dann sind C1 und C3 kurzgeschlossen. Also hat man Schwingkreis mit C =C2=2 und Parallelschaltung
von L1 und L2, also Lges = 0.5. Das ergibt Frequenz f = 1/(2*pi*sqrt(2*0.5) = 1/(2*pi) , also die gleiche Frequenz wie oben f1.
So auch in Simulation