P i P i i PPL Programmieren Programmierenin PPLin PPL

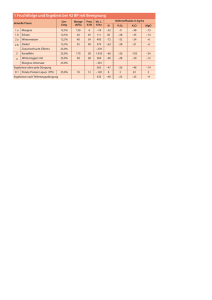
P
Programmieren
i
i PPL
in PPL
Was Sie schon immer über funktionale Programmierung wissen wollten, aber bisher nicht zu fragen wagten
g
g
PPL at a PPL at
PPL a glance
a glance
• KIV ist im wesentlichen in PPL programmiert
• PPL (proof programming language) ist eine ML‐artige funktionale Sprache
p
• PPL entstand zur Zeit von ML, Ende der 1980er
• PPL setzt die damals neuesten Konzepte um, PPL setzt die damals neuesten Konzepte um
beispielsweise eine virtuelle Maschine (SECD Maschine) und Bytecode Polymorphie Typisierung
und Bytecode, Polymorphie, Typisierung
• PPL‐Syntax ist ähnlich zu LISP (viele Klammern!)
• PPL ist statisch typisiert, Typen werden inferiert
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
2
Typinferenz
PPL 1> (+ 3 ″ab″)
Error:
types of arguments
INT x STRING
do not match type of built in function
(INT x INT -> INT)
in
(+ 3 ab)
PPL 1> (list 2 ″ab″)
Error:
Expressions
(2 n)
must be of same type, but their types
INT x STRING
are not unifiable
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
3
Typinferenz
PPL
Th
The
The
[a,
25.6.2008
1>(ppltype (list ″a″ ″b″))
t
type of
f (LIST a b) is
i (LIST (STRING))
computed substitution is ((239428) (STRING))
b]
Beweisbar korrekte Software — Sommersemester 2008
4
PPL at a PPL at
PPL a glance
a glance
• KIV hat kein
– Pattern matching
f and(true,true) = true
fun
d(t
t ) t
|
and(_,_) = false
– Modulkonzept für Code
– Automatisches Currying
(+ 2) : nat → nat
– Lazy evaluation
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
5
Ausdrücke
Ausdrücke in PPL
in PPL
• Ausdrücke werden interpretiert
• Konstante
PPL 1> 3
3
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
6
Ausdrücke
Ausdrücke in PPL
in PPL
• Ausdrücke werden interpretiert
• Konstante
PPL 1> 3
3
PPL 1>
• Variable
PPL 1> x
Error:
The identifier X has no definition
PPL 1> (def (x 1))
PPL 1> x
Wert von x
Fehlermeldung
1
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
7
Ausdrücke
Ausdrücke in PPL
in PPL
• Befehl oder Funktion
(f param1 param2 … paramn)
param1 … paramn sind wieder Ausdrücke
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
8
Funktionen
• KIV kennt 3 Arten von Funktionen
– Vordefinierte Funktionen, z.B. +, equal, emptyp
– Selbst definierte Funktionen
– Lambda‐Ausdrücke
• Wichtigstes Syntaxkonstrukt in KIV: g
y
Funktionsanwendung
(fun p
(
param1 … p
paramn)
)
Funktionsname
Ausdruck für Argument
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
9
Funktionen
• KIV kennt 3 Arten von Funktionen
– Vordefinierte Funktionen, z.B. +, equal, emptyp
– Selbst definierte Funktionen
– Lambda‐Ausdrücke
• Wichtigstes Syntaxkonstrukt in KIV: g
y
Funktionsanwendung
(fun p
(
param1 … p
paramn)
)
Ausdruck für Argument
• Beispiel: PPL 1> (+ 3 4)
7
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
10
Funktionen
• Funktionsanwendungen können geschachtelt sein. Ein Argument kann eine Funktionsapplikation sein:
PPL 1> (- 7 (+ 2 3))
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
11
Funktionen
• Funktionsanwendungen können geschachtelt sein. Ein Argument kann eine Funktionsapplikation sein:
PPL 1> (- 7 (+ 2 3))
• Funktionen werden mit lambda definiert:
p
(lambda (var1 … varn) expr)
Formaler Parameter
25.6.2008
Funktionsrumpf
Beweisbar korrekte Software — Sommersemester 2008
12
Funktionen
• Funktionsanwendungen können geschachtelt sein. Ein Argument kann eine Funktionsapplikation sein:
PPL 1> (- 7 (+ 2 3))
• Funktionen werden mit lambda definiert:
p
(lambda (var1 … varn) expr)
Formaler Parameter
Funktionsrumpf
• Beispiel: PPL 1>((lambda (x y) (*
( x y)) 3 4)
12
Bisher keine Rekursion möglich
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
13
Definition von Werten
Definition von Werten
• def bindet beliebige PPL‐Objekte an Variablen
(def (var1 expr1)
def darf nicht (def (var2 expr2)
innerhalb anderer PPL‐Ausdrücke ⁞
auftreten
(def(varn exprn)
)
• Beispiel:
p
PPL 1> (def (x 3)
(y (list t f)))
PPL 1> x
3
PPL 1> y
[T F]
[T,
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
14
Definition von Werten
Definition von Werten
• Die Ausdrücke in def werden parallel ausgewertet:
PPL 1> (def (x 0))
0
PPL 1> (def (x 3)
(y (+ 1 x)))
PPL 1> y
1
PPL 1> x
3
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
15
Funktionsdefinitionen
• Auch Funktionsrümpfe werden mit def an Namen gebunden:
PPL 1> (def (fun (lambda (x) (+ x x))))
PPL 1>
1 (f
(fun 3)
6
• Was fehlt noch: Rekursion! Dafür benützt man defrec:
Was fehlt noch: Rekursion! Dafür benützt man defrec:
PPL 1> (defrec (fac (lambda (x)
(if (
(
(= 0 x)
) 1 (
(* x (
(fac
ac (
(- x 1)))
)))
))))
def kann hier nicht anstelle von defrec
PPL 1> (fac 4)
verwendet werden, da sonst eine ggf. ,
gg
24
schon bestehende alte Definition von fac
verwendet würde.
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
16
Funktionsdefinitionen
• PPL ist higher‐order: Funktionen als Parameter und als Rückgabewerte sind zulässig:
PPL 1> (defrec (filter (lambda (test alist))
(cond ((emptyp
p yp alist) (list))
((test (car alist))
(cons (car alist) (filter test (cdr alist))))
(t (filter test (cdr alist)))
)))
PPL 1> (filter (lambda (x) (< x 10)) (list 1 2 3 11 22 33))
[1, 2, 3]
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
17
Funktionsdefinitionen
• PPL ist higher‐order: Funktionen als Parameter und als Rückgabewerte sind zulässig:
PPL 1> (defrec (filter (lambda (test alist))
(cond ((emptyp
p yp alist) (list))
((test (car alist))
(cons (car alist) (filter test (cdr alist))))
(t (filter test (cdr alist)))
)))
PPL 1> (filter (lambda (x) (< x 10)) (list 1 2 3 11 22 33))
[1, 2, 3]
PPL 1> (def (mkplusx (lambda (x) (lambda (y) (+ x y)))))
PPL 1> (mkplusx 2)
<< A FUNCTION OF TYPE (INT ->
> INT) >>
PPL 1> ((mkplusx 2) 6)
8
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
18
Typausdrücke
• PPL ist stark typisiert. Jeder PPL‐Ausdruck hat einen Typ.
• Typfehler in Funktionsdefinitionen sind unmöglich.
Typausdrücke sind:
• Typausdrücke sind:
<typevar> := *t*, *t2*, *t3*,…
<typeexpr> := <typevar>|
(<typeconstructor> <typeexpr1> … <typeexprn>)
• Typkonstruktoren sind:
–
–
–
–
25.6.2008
bool, string,
bool
string int,
int tree,
tree … (0‐stellig)
(0 stellig)
list
(1‐stellig)
Alle mkpair
(2 stellig)
(2‐stellig)
Listenelemente haben fun
(n‐stellig)
denselben Typ!
Beweisbar korrekte Software — Sommersemester 2008
19
Typausdrücke
•
25.6.2008
Einige Beispiele:
A d k
Ausdruck
T
Typ
3
(int)
″ab″
(
(string)
g)
(mkpair 3 t)
(pair (int) (bool))
(lambda (x y) (+ x y))
(fun (int)(int)(int))
(list 3)
(list (int))
nil
(list *t*)
(lambda (x) x)
(fun *t* *t*)
(lambda (x) (cons x nil))
(fun *t* (list *t*))
Beweisbar korrekte Software — Sommersemester 2008
20
Typausdrücke
•
•
Einige Beispiele:
A d k
Ausdruck
T
Typ
3
(int)
″ab″
(
(string)
g)
(mkpair 3 t)
(pair (int) (bool))
(lambda (x y) (+ x y))
(fun (int)(int)(int))
(list 3)
(list (int))
nil
(list *t*)
(lambda (x) x)
(fun *t* *t*)
(lambda (x) (cons x nil))
(fun *t* (list *t*))
Pretty printing von Typen in KIV anders:
Pretty‐printing
von Typen in KIV anders:
–
–
–
–
25.6.2008
(int) ⇒ int
(list (int)) ⇒ int*
(fun (
(
(int)
) (
(int))
)) ⇒ int -> int
(pair (int) (int)) ⇒ [ int | int ]
Beweisbar korrekte Software — Sommersemester 2008
21
Vordefinierte Funktionen
Vordefinierte Funktionen
• Es gibt in PPL eine Reihe von vordefinierten Funktionen, z.B.:
– +, ‐, *, div
– <, >, =
– (list arg1,…,argn), car, cdr, emptyp,
member, append
– (mkpair arg1 arg2), fst, snd
– (and arg1 … argn), or, not
• Details siehe Praktikumsdoku
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
22
Listenfunktionen
• Listen sind in PPL vordefiniert. Wichtige Funktionen:
• nil oder (list): Erzeugt leere Liste
expr2): Fügt expr1
Fügt expr1 vorne an Liste vorne an Liste
• (cons expr1 expr2):
expr2 and
• (append expr1 expr2):
expr2): Hängt expr2
Hängt expr2 hinten an hinten an
expr1 an
• (car
(
expr): Liefert das erste Element von expr
) Li f t d
t El
t
• (cdr expr): Liefert die Restliste (ohne das erste Element) von expr
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
23
Beispiele zu Listen
Beispiele zu Listen
PPL
1
PPL
[2
[2,
PPL
[2]
PPL
F
PPL
25.6.2008
1> (car (cons 1 (list 2 3)))
1> (cdr (append (list 1 2) (list 3 4)))
3
3, 4]
1> (cons 2 nil)
1> (emptyp (cons t nil))
1>
Beweisbar korrekte Software — Sommersemester 2008
24
Kontrollstrukturen
• PPL kennt nur wenige Kontrollstrukturen: g
– Fallunterscheidungen
– Definition lokaler Variablen
– backtracking
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
25
Fallunterscheidung
• Fallunterscheidungen werden mit cond oder if
durchgeführt:
– (if condexpr thenexpr elseexpr)
– (cond (test1 expr1)
(test2 expr2)
⁞
(t exprn))
• Beispiele:
B i i l
PPL 1> (if t (+ 2 3) 0)
5
PPL 1> (cond ((emptyp (list)) 0)
(t 1))
(
))
0
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
26
Lokale Variablen
Lokale Variablen
• Lokale Variablen werden mit let* deklariert:
(let* ((var1 expr1)
(var2 expr2)
⁞
(varn exprn))
expr)
p )
• Zuerst wird expr1 ausgewertet und das Ergebnis an var1 gebunden, dann expr2, in der var1
gebunden dann expr2 in der var1 benutzt benutzt
werden kann, usw.
• Das Ergebnis des let*
Das Ergebnis des let* ist expr
ist expr
• Bei let (statt let*) werden expr1,…,exprn
parallel ausgewertet
ll l
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
27
Lokale Variablen
Lokale Variablen
• Beispiel:
PPL 1> (let* ((x (+ 2 5))
(y (+ x x ))
)
(+ y y ))
28
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
28
backtracking
• KIV hat ein generisches System für Exceptions und Exception‐Handler
g
p
g
• Hier nur ein wichtiger Spezialfall für backtracking
• backtracking ist in PPL sehr leicht zu realisieren
• backtracking wird mit dem Kommando (fail)
wird mit dem Kommando (fail)
ausgelöst oder durch andere vordefinierte Funktionen wie makettree refine,
wie makettree,
refine infer,
infer match
• Die Fortsetzungsstelle für die Programmausführung wird mit orL
it L deklariert:
d kl i t
(orL expr1 expr2)
Wird zuerst ausgewertet
25.6.2008
Falls fail in expr1 wird expr2 ausgewertet
Beweisbar korrekte Software — Sommersemester 2008
29
Backtracking
• Beispiele
PPL 1> (orL 3 4)
3
PPL 1> (orL (fail) (+ 3 (fail)) 4)
4
PPL 1> (equal (fail) (fail))
Error:
operation FAIL failed
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
30
Schnittstelle zum Dateisystem
Schnittstelle zum Dateisystem
• Laden von PPL‐Source‐Dateien: load und require
PPL 1> (load ″~/ppl/proplogic″)
;;; loading proplogic
;;; loaded proplogic
• exit in einer Datei beendet das Laden an dieser Stelle • Schnittstelle zum Dateisystem: cd, pwd
PPL 1> (cd ″~″)
T
PPL 1> (pwd)
/home/dominik
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
31
Ein‐‐/Ausgabe
Ein
• Textausgabe:
PPL 1>
x wird
PPL 1>
10
PPL 1>
4
25.6.2008
before
(def (x (before ″x wird initialisiert″ 3)))
initialisiert
(def (y (before (+ x 7) (+ x 1))))
y
Beweisbar korrekte Software — Sommersemester 2008
32
Ein‐‐/Ausgabe
Ein
• Mit read kann man Eingaben vom Benutzer verlangen
(read x (<typ> expr))
Datentyp der Eingabe
25.6.2008
Ausdruck für das Ergebnis des read
Beweisbar korrekte Software — Sommersemester 2008
33
Ein‐‐/Ausgabe
Ein
• Beispiel für read:
PPL 1> (read x ((INT) x))
PPL 2> ″c″
c
PPL 2> exit
Error:
no positive type case for read found in function
<-PPL
PPL 1> (
(def (y (
(read x ((
((INT)
) (
(* x x)))))
)))))
PPL 2> 4
4
PPL 2> exit
it
PPL 1> y
16
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
34
Formeln
Formeln und Sequenzen in KIV
und Sequenzen in KIV
• Datentypen für Formeln (fl) und Sequenzen (seq) sind in KIV fest eingebaut
p
g
g g
• Werden am PPL‐Prompt wie folgt eingegeben:
1. Durch direkte Konstruktion der PPL‐Datenstruktur
PPL 1> (mkall (mkvl1 (list (mkxov
( k
(mkxov
(mkeq (mkxov (mksym
(mkxov (mksym
all s
s, s0
s0. s = s0
PPL1>
(mksym ″s″))
( k
(mksym
″ 0″))))
″s0″))))
″s″))
″s0″))))
2. Über den Parser
PPL 1> % ″all s , s0 . s = s0″
all s, s0. s = s0
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
35
Formeln
Formeln und Sequenzen in KIV
und Sequenzen in KIV
• Man benötigt allerdings zuerst eine geeignete Signatur
• Variante 1: Aus Projekt laden
PPl 1> (resetsig)
PPL 1>
1 (def (dvg
(load-devgraph-dir-til-ok
(mkdirectory ″?/lib/basic″))))
PPL 1> (add-specsig-dvg ″nat″ dvg)
T
PPL 1> %″0 +1 = 0 + 1″
Top‐level Spezifikation, 0 +1 = 0 + 1
deren Signatur man PPL 1>
nutzen will
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
36
Formeln
Formeln und Sequenzen in KIV
und Sequenzen in KIV
• Variante 2: Eingabe am PPL‐Prompt
PPL 1> %″sorts s ;″
[s]
PPL 1> %″variables s, s0, s1 : s ;″
[s, s0, s1]
• Aus Formeln kann man Sequenzen bauen:
PPL 1> (def (formel1 %″not n +1 +1 = 0 +1″))
PPL 1> (def (formel2 %″ex n . not (n = 0 +1)″))
PPL 1> (def (seq
q (mkseq
q
(mkfl1 (list formel1 %″true″))
(mkfl1 (list formel2)))))
PPL 1> seq
not n +1 +1 = 0 +1, true |- ex n. not n = 0 +1
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
37
Beweisbäume
Beweisbäume in KIV
in KIV
• (Beweis‐)Bäume sind ebenfalls ein fest in KIV eingebauter Datentyp
• Ein Beweisbaum ist entweder
– Eine Sequenz
PPL 1> (ppltype seq)
The type of SEQ is (TREE)
The computed substitution is NIL
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
38
Beweisbäume
Beweisbäume in KIV
in KIV
– Ein zusammengesetzer Baum
PPL 1>
1 (
(ppltype
l
di
dis_r)
)
The type of DIS_R is (TREE)
The computed substitution is NIL
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
39
Beweisregeln
Beweisregeln als Bäume
als Bäume
• Sequenzenkalkülregeln werden als Bäume repräsentiert
Konklusion und Prämissen enthalten Metavariablen, die durch K
kl i
dP ä i
h l
M
i bl
di d h
pattern‐matching instanziiert werden
– Formeln: $phi,
$phi $psi
– Formellisten: $Gamma, $Delta
– Programme:
P
$ l h $beta
$alpha,
$b t
– Boolesche Werte: $epsilon
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
40
Matching von Formelpatterns
von Formelpatterns
PPL 1> (def (seq (mkseq
(mkfl1 (list))
(mkfl1 (list %″n = n or n < n″)
))))
|- n = n or n < n
PPL 1> (concl dis_r)
$Γ |- $ϕ or $ψ, $Δ
PPL 1> (matchp seq (concl dis_r))
T
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
41
Beweisbäume konstruieren
Beweisbäume konstruieren
• Beweisbäume werden durch Regelanwendungen konstruiert
,
ein Beweisbaum an einer offenen • In PPL heißt das, daß
Prämisse um einen Regelbaum erweitert wird. Dazu:
1. Matchen der Konklusion des Regelbaums und der Prämisse g
des Beweisbaums
2. Instanziieren der Prämisse des Regelbaums
3. Kombination der beiden Teilbäume zu einem neuen Baum
• Dies erledigt die Funktion refine
g
e
e
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
42
refine
PPL 1> seq
|- n = n or n < n
PPL 1> (refine seq 1 dis_r)
** A TREE **
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
43
refine
PPL 1> (def (id (lambda (x) x)))
PPL 1> (orL (refine (id seq) 1 neg_r)
(before ″Pech gehabt″ seq))
Pech gehabt
|- n = n or n < n
PPL 1>
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
44
refine und und backtracking
und backtracking
PPL 1> (orL (refine(id
(refine(id
(refine(id
(refine(id
** A TREE **
PPL 1>
25.6.2008
seq)
seq)
seq)
seq)
Beweisbar korrekte Software — Sommersemester 2008
1
1
1
1
neg_r)
con_r)
imp_r)
dis_r))
45
Fehlersuche
• PPL hat einen Debugger: Siehe Praktikumsdoku
• Funktionsaufrufe werden mit dem Tracer überwacht. Er g
gibt bei jedem Funktionsaufruf die Parameterwerte und j
beim Verlassen der Funktion den Ergebniswert aus.
Aufruf erfolgt mit (trace fun)
• Aufruf erfolgt mit (trace
• Will man nur manche Argumente sehen:
(trace (fun
0
2
3))
Ergebnis ausgeben
Aufrufparameter 2 und 3 ausgeben
und 3 ausgeben
• Das Tracen wird beendet mit ( t
(untrace
f )
fun)
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
46
Der Tracer
Der Tracer
PPL 1> (trace reverse-h)
(reverse-h)
PPL 1> (reverse (list 1))
+++ REVERSE-H +++++++++++++++++++
first argument:
[1]
second argument:
[]
++++++ REVERSE-H ++++++++++++++++
first argument:
[]
second argument:
g
[1]
------ REVERSE-H ---------------[1]
--- REVERSE-H ------------------[1]
25.6.2008
Beweisbar korrekte Software — Sommersemester 2008
47