Tiefensuche – Überblick (1)
Werbung

Tiefensuche – Überblick (1)
Die Tiefensuche durchsucht wie die Breitensuche
einen Graphen.
Allerdings wird immer eine Kante vom zuletzt entdeckten Knoten v erforscht. Gibt es keine solche
Kante mehr, wird zum Knoten, von dem aus v entdeckt wurde, zurück gegangen (backtracking).
Suche wird so lange fortgesetzt, wie noch nicht besuchte Knoten existieren.
Sind alle von einem Knoten aus erreichbaren Knoten
entdeckt und existieren noch unentdeckte Knoten,
so beginnt Tiefensuche mit einem noch nicht entdeckten Knoten.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
1
Tiefensuche – Überblick (2)
Definieren Vorgänger π[v ] wie bei Breitensuche
und definieren Gπ := (V,E π ) durch
E π := {(π[v ], v ) | v ∈ V }.
Gπ ist kein Baum, sondern nur ein Wald, d.h. ein
Graph zusammengesetzt aus Bäumen auf disjunkten Knotenmengen. Dieser Wald wird Tiefensuch-Wald genannt.
Benutzen Färbung von Knoten wie bei Breitensuche.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
2
Tiefensuche – Überblick (3)
Definieren zusätzlich zu π[v ], d[v ] noch Feld f [v ].
Dabei ist d[v] der Zeitpunkt, an dem v entdeckt wird
und f [v ] ist der Zeitpunkt, an dem Adj[v ] vollständig
untersucht wurde.
Es gilt 1 ≤ d[v ] < f [v ] und f [v ] ≤ 2 V . Denn in jedem
Schritt wird ein neuer Knoten entdeckt oder die Durchsuchung eine Adjazenzliste wird beendet.
Vor d[v ] ist v weiss, zwischen d[v ] und f [v ] ist v grau,
nach f [v ] ist v schwarz.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
3
Pseudocode für Tiefensuche
DFS (G )
1 for jeden Knoten u ∈ G
2
do color [u] ← WHITE
3
π [u] ← NIL
4 time ← 0
5 for jeden Knoten u ∈ G
6
7
do if color [u] = WHITE
then DFS - Visit(u)
DFS − Visit (u )
1 color [u] ← GRAY
2 time ← time + 1
3 d[u] ← time
4 for jeden Knoten v ∈ Adj [u ]
5
6
do if color [v ] = WHITE
then π [v ] ← u
7
DFS - Visit(v )
8 color [u] ← BLACK
9 time ← time + 1
10 f [u] ← time
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
4
Illustration Tiefensuche (1)
u
1/
v
w
u
1/
v
2/
w
x
y
z
x
y
z
u
1/
v
2/
w
u
1/
v
2/
w
4/
3/
x
y
3/
x
SS 2006
y
z
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
z
5
Illustration Tiefensuche (2)
u
1/
v
2/
w
u
1/
v
2/
w
B
4/
3/
x
y
u
1/
v
2/
z
w
4/5
3/
x
y
u
1/
v
2/7
w
B
B
4/5
3/6
x
y
SS 2006
z
z
4/5
3/6
x
y
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
z
6
Illustration Tiefensuche (3)
u
1/
v
2/7
w
B
F
4/5
3/6
x
y
z
u
1/8
v
2/7
w
9/
F
B
3/6
x
y
z
v
2/7
w
B
4/5
3/6
x
y
u
1/8
F
4/5
SS 2006
u
1/8
z
v
2/7
C
B
4/5
3/6
x
y
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
w
9/
z
7
Illustration Tiefensuche (4)
u
1/8
F
v
2/7
4/5
3/6
x
y
u
1/8
v
2/7
F
v
2/7
w
9/
C
B
4/5
3/6
10/
z
x
y
z
w
9/
u
1/8
v
2/7
w
9/
C
B
F
4/5
3/6
10/
x
y
z
SS 2006
u
1/8
C
B
F
w
9/
B
C
B
4/5
3/6
10/11
x
y
z
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
B
8
Illustration Tiefensuche (5)
u
v
1/8
F
SS 2006
2/7
9/12
C
B
4/5
x
w
3/6
y
10/11
z
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
B
9
Tiefensuche - Laufzeitanalyse
Satz 15.8: Bei Eingabe von Graph G=(V,E) besitzt
Algorithmus DFS Laufzeit O ( V + E ).
Analyse: Wie bei Breitensuche. Nutzen aus dass
Gesamtgröße aller Adjazenzlisten O (E )
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
10
Tiefensuche – Eigenschaften (1)
Satz 15.9: Für jede Tiefensuche eines gerichteten oder
ungerichteten Graphen G=(V,E) und für je zwei
Knoten u,v des Graphen G trifft genau eine der drei
folgenden Aussagen zu:
1. Die Intervalle [d[u ], f [u ]] und [d[v ], f [v ]] sind disjunkt
und weder u noch v ist im Tiefensuch-Wald ein
Nachfahre des jeweils anderen Knotens.
2. Das Intervall [d[u ], f [u ]] ist im Intervall [d[v ], f [v ]]
enthalten und im Tiefensuch-Wald ist u ein
Nachfahre von v.
3. Das Intervall [d[v ], fv ] ist im Intervall [d[u ], f [u ]]
enthalten und im Tiefensuch-Wald ist v ein
Nachfahre von u.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
11
Tiefensuche – Eigenschaften (2)
Korollar 15.10: Im Tiefensuch-Wald ist Knoten v ein
Nachfahre von Knoten u ≠ v dann und nur dann, wenn
gilt d[u] < d[v ] < f [v ] < f [u].
Satz 15.11: Im Tiefensuch-Wald eines Graphen G=(V,E)
ist v ein Nachfahre von u dann und nur dann, wenn
zum Zeitpunkt, an dem die Suche u entdeckt, v von u
aus auf einem Pfad erreichbar ist, der nur weisse
Knoten enthält.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
12
Ergebnis einer Tiefensuche mit Klammerung
y
z
s
t
3/6
2/9
1/10
11/16
F
B
4/5
C
x
7/8
C
C
w
12/13
v
B
14/15
C
u
s
t
z
v
y
u
w
x
1
(s
SS 2006
2
(z
3
(y
4
(x
5
x)
6
y)
7
(w
8
w)
9
z)
10
s)
11
(t
12
(v
13
v)
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
14
(u
15
u)
16
t)
13
Ergebnis einer Tiefensuche (2)
y
z
s
t
3/6
2/9
1/10
11/16
F
B
4/5
7/8
C
x
C
C
w
12/13
v
s
B
C
14/15
u
t
B
C
B
F
z
y
C
v
C
u
w
C
x
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
14
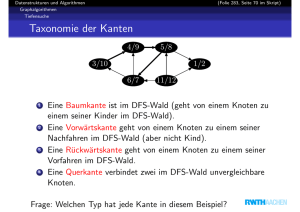
Klassifikation von Kanten
Betrachten Graphen G=(V,E) und einen Tiefensuch –
Wald Gπ = (V,E π ) entstanden durch eine Tiefensuche.
1. Kanten in G, die auch in Gπ liegen, heissen
Baumkanten.
2. Kanten (u,v), die eine Knoten u zu einem Knoten
v verbinden, der in Gπ ein Vorfahre von u ist,
heissen Rückkanten.
3. Kanten (u,v), die einen Knoten u zu einem Knoten
v verbinden, der in Gπ ein Nachfahre von u ist,
heissen Vorwärtskanten.
4. Die restlichen Kanten heissen Kreuzungskanten.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
15
Ergebnis einer Tiefensuche (2)
B:= Rückkante
y
z
s
t
3/6
2/9
1/10
11/16
F:= Vorwärtskante
C:= Kruezungskante
F
B
4/5
7/8
C
x
C
12/13
C
w
v
B
C
14/15
u
Baumkante
s
t
B
C
B
F
z
y
C
v
C
u
w
C
x
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
16
Zusammenhangskomponenten
Definition 15.11: Ein ungerichteter Graph G=(V,E) heisst
zusammenhängend, wenn es für je zwei Knoten u,v
in G einen Pfad in G gibt, der die Knoten miteinander
verbindet.
Definition 15.12: Die Mengen C1,K, Ck ⊆ V heissen die
Zusammenhangskomponenten von G, wenn
1.
2.
SS 2006
Ci ∩ C j = { } und C1 ∪ L ∪ Ck = V
Zwei Knoten u,v in G sind genau durch einen
Pfad in G miteinander verbunden, wenn es
ein j, 1 ≤ j ≤ k , gibt, so dass u, v ∈ C j .
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
17
Zusammenhangskomponenten - Beispiel
a
b
e
g
d
h
i
f
c
Pfad von a nach f
Zusammenhangskomponenten
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
18
Zusammenhangskomponenten - Berechnung
Satz 15.13: Für einen ungerichteten Graphen G=(V,E)
sind die Zusammenhangskomponenten C1,K, Ck
gegeben durch die Knotenmengen der Bäume eines
beliebigen Tiefensuch-Waldes von G.
Korollar 15.14: Die Zusammenhangskomponenten eines
ungerichteten Graphen G können in Zeit O ( V + E )
berechnet werden.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
19
Starke Zusammenhangskomponenten
Definition 15.15: Ein gerichteter Graph G=(V,E) heisst
stark zusammenhängend, wenn es für je zwei
Knoten u,v in G gerichtete Pfade von u nach v und
von v nach u in G gibt.
Definition 15.16: Die Mengen C1,K, Ck ⊆ V heissen die
starke Zusammenhangskomponenten von G, wenn
1.
2.
SS 2006
Ci ∩ Cj = { } und C1 ∪ L ∪ Ck = V
Für je zwei Knoten u,v existieren genau dann
gerichtete Pfade von u nach v und von v nach
u, wenn es ein j, 1 ≤ j ≤ k , gibt, so dass u, v ∈ Cj .
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
20
Starke Zusammenhangskomponenten - Beispiel
1
2
3
4
5
6
Starke Zusammenhangskomponenten
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
21
Starke Zusammenhangskomponenten - Berechnung
Satz 15.17: Die starken Zusammenhangskomponenten
eines gerichteten Graphen G können in Zeit O ( V + E )
berechnet werden.
SS 2006
Datenstrukturen und Algorithmen
15. Elementare Graphalgorithmen
22