Kernphysik

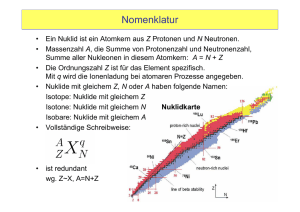
Wintersemester 2011/2012
Radioaktivität und Radiochemie
Kernphysik
27.10.2011
Udo Gerstmann
Bundesamt für Strahlenschutz
[email protected] & [email protected]
089-31603-2430
Der Atomkern
• besteht aus Protonen und Neutronen (Nukleonen)
• hat einen Durchmesser von ca. ein Zehn- bis
Hunderttausendstel der Elektronenhülle
• hat eine Massendichte von ca. 2∙1017 kg m-3
• bislang gibt es kein Modell zur umfassenden Beschreibung
aller Eigenschaften von Atomkernen
• Man kennt ca. 280 Nuklide, von denen 271 stabil sind. Es
handelt sich um 162 g,g-Kerne, 104 g,u- und u,g-Kerne sowie
um 5 u,u-Kerne (2H, 6Li, 10B, 14N, 50V)
Fundamentale Wechselwirkungen
Teilchen und Felder
Wechselwirkung
Physikalisches
Phänomen
Relative
Stärke
Effektive
Reichweite (m)
Wechselwirkungsfeldquanten
Spin
Masse
Materiefeld
Teilchen
Spin
Art der WW zw.
identischen
Teilchen
stark
Kernbindung
1
10-15
Gluonen
1ħ
0
Quarks
½ħ
abstoßend
elektromagnetisch
Elektrizität
Magnetismus
Optik aller Wellenlängen
10-2
∞
Photonen
1ħ
0
Quarks,
geladene
Leptonen
½ħ
abstoßend
schwach
radioaktiver Zerfall
10-5
10-18
W±, Z, Bosonen
1ħ
≈ 100 GeV
Quarks,
Leptonen
abstoßend
Gravitation
gekrümmtes Raum-ZeitKontinuum
10-38
∞
Gravitation
2ħ
0
alle Teilchen
anziehend
Elementarteilchen - Quarks
Name
Symbol
El. Ladung (e0) Ruheenergie (GeV)
Up
u
2/3
1,5.10-3 - 4.10-3
Down
d
-1/3
4.10-3 - 8.10-3
Charme
c
2/3
1,15 - 1,35
Strange
s
-1/3
0,080 - 0,130
Top
t
2/3
170 - 188
Bottom
b
-1/3
4,1 - 4,4
Generation 1
Generation 2
Generation 3
Elementarteilchen - Leptonen
Name
Symbol El. Ladung (e0)
Ruheenergie (MeV)
Elektron
e-
-1
0,510998902
Elektron-Neutrino
νe
0
< 2,5.10-6
Myon
µ
-1
105,658357
Myon-Neutrino
νµ
0
< 0,19
Tau
τ
-1
1776,99
Tau-Neutrino
ντ
-1/3
4,1 - 4,4
Generation 1
Generation 2
Generation 3
Beta-Zerfall
d
d
d
u
u
u
ßt½ = 614 s
-⅓
⅔
-⅓
Neutron
0
Feynman-Diagramm
Quelle: Wikipedia
-⅓
⅔
⅔
Proton
+1
Bindungs- und Separationsenergie, Massendefekt
mK(Z,N) c2 = Z mp c2 + N mn c2 - ∆m(Z,N) c2
ES = - EB
z. B. Separation eines Protons: ES(p) = mK(Z,N) c2 - mK(Z-1,N) c2 - mp c2
ES(n)
3.937 MeV
209Pb
Z = 82, N = 127
ES(p)
3.799 MeV
209Bi
Z = 83, N = 126
Definition des Masse-Standards
mK(Z,N) c2 = Z mp c2 + N mn c2 - ∆m(Z,N) c2
mA(Z,N) c2 = Z (mp + me) c2 + N mn c2 - ∆m(Z,N) c2 - EB(e-)
mp c2 = 938,27231 MeV
mn c2 = 939,56563 MeV
12C
6 mpc2
5629,6320 MeV
6 mnc2
5637,3938 MeV
6 mec2
3,0660 MeV
Summe
- ∆m(6,6)c2
11270,0918 MeV
92,1618 MeV
11177,9300 MeV
1 u = mu = 931,5 MeV c-2 = 1,661 . 10-27 kg
Experimentelle mittlere Bindungsenergie pro Nukleon
Kernmodelle - Übersicht
• keines der bestehenden Modelle kann alle Eigenschaften des
Atomkerns ausreichend beschreiben!
starke WechselwirkungsModelle
unabhängige-TeilchenModelle
Grundannahme
Atomkern besteht aus eng
gepaarten Nukleonen
die Nukleonen bewegen
sich relativ frei im Kern
Beispiel(e)
Tröpfchen-Modell
Alpha-Teilchen-Modell
Fermigas-Modell
Schalenmodell
Flüssigkeitströpfchen-Modell
(liquid drop model)
• "Nukleonen im Kern wie Moleküle in einer Flüssigkeit"
–
–
–
–
nicht komprimierbar
Bindungskräfte kurzer Reichweite
Kondensationswärme bzw. Bindungsenergie
"Oberflächenspannung"
EB = EVolumen + EOberfläche + ECoulomb + EAsymmertrie + EPaarung
Flüssigkeitströpfchen-Modell
(liquid drop model)
EB = EVolumen + EOberfläche + ECoulomb + EAsymmertrie + EPaarung
EVolumen
= aV A
(da V ~ R3 bzw. R ~ A⅓)
EOberfläche = - aO A⅔
ECoulomb
(da O ~ R2)
= - aC Z2 R-1 = -aC Z2 A-⅓
EAsymmertrie = - aA (N-Z)2 A-1
EPaarung
= aP A-½
aV ≈ 15,5 MeV
aO ≈ 16,8 MeV
aC ≈ 0,715 MeV
aA ≈ 23 MeV
aP ≈ 11,3 MeV (gg)
- 11,3 MeV (uu)
0 (ug, gu)
Mittlere Bindungsenergie pro Nukleon als Funktion
der Massenzahl nach Bethe-Weizsäcker
Erklärbar mit dem Tröpfchenmodell:
Energiegewinn bei Kernumwandlungen
• Verschmelzung von leichteren Kernen
D + T  4He + n + 17,6 MeV
• Spaltung von schwereren Kernen
235U
+ n  93Sr + 140Xe + 3 n + 198 MeV
Isobaren-Parabeln
allg. bei konst. A  EB = α Z2 + β Z + γ + δ/A  Paarungsterm
Parabel mit Scheitelpunkt ZA = A/(1,98 + 0,01493 A⅔)
Trägt man ZA als Funktion von A in die Nuklidkarte ein, so erhält
man die Linie der ß-Stabilität
Bindungsenergie für Nuklide mit ungerader Nukleonenzahl
Bindungsernergie für Nuklide mit gerader Nukleonenzahl
Einzelteilchen-Schalenmodell
• beruht auf quantenmechanischen Gesetzmäßigkeiten.
• gut zur Erklärung einiger empirischer Erfahrungen:
– Häufigkeit von gg-, ug/gu- und uu-Kernen
– viele Isotone und Isotope bei magischen Nukleonenzahlen
• Z = 2, 8, 20, 28, 50, 82, (114, 120, 164, 210)
• N = 2, 8, 20, 28, 50, 82, 126, (184, 196, 228, 272, 318)
• Kerne mit magischen Nukleonenzahlen zeichnen sich aus durch:
– hohe erste Kernanregungsenergien
– kleine Einfangsquerschnitte für Kernreaktionen
– hohe Seprationsenergien für Protonen bzw. Neutronen
ES(n)
ES(p)
7.367 MeV
208Pb
Z = 82, N = 126
3.937 MeV
209Pb
Z = 82, N = 127
8.007 MeV
208Pb
Z = 82, N = 126
3.799 MeV
209Bi
Z = 83, N = 126
Einzelteilchen-Schalenmodell
7
10
9
6
8
7
Zahl stabiler Isoto
Zahl stabiler Isoto
5
4
3
6
5
4
3
2
2
1
1
0
0
10
20
30
40
50
60
70
Neutronenzahl
80
90
100
110
120
10
20
30
40
Protonenzahl
50
60
70
80
Häufigkeit der Seltenen Erden (Harkin'sche Regel)
Elemente mit gerader Ordnungszahl sind häufiger als benachbarte Elemente
mit ungerader Ordnungszahl.
Weitere Modelle
Fermigas-Modell
beschreibt die Konstitutenten des Kerns als
statistisches Ensemble mit der Fermi-DiracStatistik
α-Teilchen-Modell
berücksichtigt α-Teilchen als stabile
Untereinheiten des Kerns
vereintes Modell
...
Potentialtopf-Modell
...
...
...
Weitere Eigenschaften von Atomkernen
•
•
•
•
•
Spins
elektrische und magnetische Momente
Parität
Anregungsenergien
Isospin
Schalenmodell-Zustände
mit Berücksichtigung der Spin-Bahn-Kopplung
Einzelniveaus als Funktion des Deformationsparameters
Zusammenfassung
• Atomekerne sind aus Neutronen und Protonen
zusammengesetzt, die durch die Restwechselwirkungen aus
der starken Wechselwirkung zwischen den
Nukleonenbausteinen Quarks aneinander gebunden sind.
• Kernkräfte sind kurzweitige Paarkräfte, die Nukleonen in
unmittelbarem Kontakt aneinander binden. Kernmaterial hat
eine extrem hohe Dichte.
• Mit zunehmender Massenzahl wird die Stabilität der Kerne
eine anwachsender Neutronenüberschuss benötigt, der bei
schweren Kernen bis etwa 50 % betragen kann.
• Wegen des Fehlens einer primären zentralen Kernkraft
werden Atomkerne durch eine Reihe quantitativer
Kernmodelle beschrieben, die je nach Anwendungszweck
ausgewählt werden, aber jeweils nur Teilaspekte der
Kernphysik beschreiben können.
Zusammenfassung
• Das Tröpfchenmodell hat sich als ein für pauschale
Energieberechnungen sehr geeignetes Kernmodell erwiesen, das
sowohl die Stabilität als auch die Instabilität (Radioaktivität) von
Atomkernen pauschal vorhersagen kann.
• Es versagt aber bei der Energieberechnung individueller Kerne,
vor allem wenn diese sich weit entfernt vom Stabilitätsbereich
befinden.
• Kerne können wie Elektronen in den Atomhüllen durch
Energiezufuhr in höherenergetische Zustände angeregt werden.
• Beim Zerfall bzw. der Abregung dieser Zustände kommt es zur
Emission charakteristischer Kernstrahlung, i. d. R.
Gammastrahlung
Radioaktiver Zerfall: Erhaltungssätze
X → Y +R
•
•
•
•
•
•
Energie:
Impuls:
Ladung:
Nukleonenzahl:
Kernspinquantenzahl:
Q-Wert
EX=EY+ER
mXvX=mYvY+mRvR
ZX=ZY+ZR
AX=AY+AR
∆I = 0, 1, 2, 3, ...
Alpha-Zerfall
A
Z
241
95
241,056822
-237,048166
-4,002603
0,006053
Q = 5,63 MeV
X→
Am →
A−4
Z −2
X + He
237
93
4
2
Np + He
4
2
E = m v2
1 u = 931,5 MeV
ENp vNp = Eα vα
Eα = mNp/mα ENp
Eα = 5,63 MeV/(mα/mNp +1) = 5,54 MeV
α-Zerfall
• beim α-Zerfall ist zusätzlich die hohe Bindungsenergie des αTeilchens zu beachten!
ES(α) = mK(Z,N) c2 - mK(Z-2,N-2) c2 - 2mpc2 - 2mnc2 - EB(Z=N=2)
Zusammenhang Energie-Halbwertszeit bei Alphastrahlern
12000
11000
Geiger-Nuttall-Regel
log λ = a + b . log E
10000
Zerfallsenergie in keV
9000
8000
7000
6000
5000
4000
3000
2000
1000
0
1E-18
1E-15
1E-12
1E-9
1E-6
1E-3
1E+0
1E+3
Halbwertszeit in Jahren
1E+6
1E+9
1E+12
1E+15
1E+18
α-Zerfall
PROTONENZERFALL
• nur bei ca. 10 künstlich hergestellten Nukliden
• entdeckt 1981 durch Beschuss von 96Ru mit 261-MeV-58NiIonen
96
58
Ru ( Ni , p2n )
p + ,t 1 =85 ms
Lu   →
151
2
150
Yb
CLUSTEREMISSION
• selten, aber kommt in der Natur vor
• 1984 bei 223Ra entdeckt
14
223
C ,t 1 ≈1010 a
Ra    →
2
209
Pb
Beta-Zerfall
p+ → n + ß+ + ν
X + ß+ + ν
A
Z
X→
A
Z −1
13
6
N→
13
6
C + ß+ + ν
n → p+ + ß− + ν
A
Z
X→
Cs →
137
X + ß− + ν
A
Z +1
137 m
Ba + ß − + ν
ß-Teilchen - Energiespektrum
Gammastrahlung nach ß--Zerfall
Gamma-Strahlung: Isobarenparabel A = 60
Konversionselektronen
Nuklide
E γ (keV)
Iγ
E ß-
α
22Na
1.275
100 %
-
6,7 . 10-7
14
9%
13
8,2
122
87 %
115
0,02
40
9%
34
22
39
0,01 %
33
461
52
0,02 %
47
269
57Co
129I
239Pu
Karlsruher Nuklidkarte
Karlsruher Nuklidkarte
Karlsruher Nuklidkarte
Beispiel: 146Pm
Z
63
62
61
60
59
N=
82
83
84
85
86
87
88
89
90