Zeitschrift für Naturforschung / B / 21 (1966) - ZfN - Max

366
H. POSSNER UND H. GRIMM
Zur Häufigkeitsverteilung der Sequenzen und Nucleotide für Polynucleotidketten
der DNS
H e in z P o s s n e r
und
H il m a r G r im m *
Institut für Mikrobiologie und experimentelle Therapie Jena der Deutschen Akademie der Wissen­
schaften zu Berlin (Direktor: Prof. Dr. med. H. K n ö l l )
(Z. Naturforschg. 21 b, 366—372 [1966]; eingegangen am 28. Juli 1965)
Es werden Tabellen und Diagramme zur Häufigkeitsverteilung der Nucleotid-Sequenzen der
DNS aufgestellt. Sie beziehen sich auf die von C h a r g a f f und H a b e r m a n n entwickelten Methoden
der Sequenz-Analytik, mit deren Hilfe die Purin- bzw. Pyrimidinbasen der DNS quantitativ abge­
spalten werden können. Die mathematische Berechnung der Häufigkeiten der Sequenzketten unter­
schiedlicher Länge beruht auf einem Modell, bei dem n gleichartige Nucleotide auf die verschie­
denste Art und Weise zu Sequenzen zusammengefügt werden. (Zerlegung der ganzen Zahl n in
ganzzahlige Bestandteile = Partitionen.) Nach den Gesetzen der Kombinatorik wird die diskrete
Verteilung der Sequenz- bzw\ Nucleotidhäufigkeiten auf die ganzzahligen Sequenzen von 1 bis n
in einem Faden der abgebauten DNS für die Sequenztypen n = l , . . . , 27 berechnet. Dabei stellt
die Zahl n die Anzahl der Nucleotide in der längsten, für die betreffende DNS charakteristischen,
Polynucleotidkette dar. Die daraus abgeleiteten theoretischen Werte für die relativen Häufigkeiten
in % für die Sequenzen und Nucleotide und die zugehörigen Werte für die Mol.-Gew. der DNS
sind aus 3 weiteren Tabellen und 2 Diagrammen zu entnehmen.
3 und seinen M itarb b . 4 beobachtet w urde. Da
die T und C nicht untersch eid b ar sind, setzen w ir
T = C = a und denken uns den linken D oppelstrang
in der durch p u n k tierte L inien v erbundenen W eise
zu einem S trang m it folgender K ette von Sequenzen
unterschiedlicher Länge vereinigt
Bereits von C h a r g a f f und M ita r b b .1 w urde eine
M ethode (kontrollierte E inw irkung von Salzsäure)
angegeben, m it deren H ilfe die P u rin b asen A denin
(A) und G uanin (G) aus DNS quantitativ abge­
spalten w erden können, w ährend die P y rim id in ­
basen Cytosin ( C ) und Thym in (T) zunächst an das
Z uckerphosphat-G erüst gebunden bleiben. Diese sog.
A p u rin säu re kann durch w eiteren A bbau schließlich
in U ntereinheiten von unterschiedlicher Gliedzahl
zerlegt w erden, die den nachbarständigen P yrim idinnucleotiden (C luster) in der ursprünglichen DNS
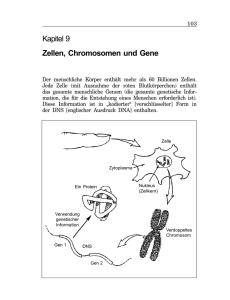
entsprechen (s. A bb. 1 ). Die analytische T rennung
solcher P yrim idinsequenzen erfolgt durch S äulen­
chrom atographie, wobei der A nteil der einzelnen
Mono- und O ligonucleotide durch M essung der A b­
sorption bei 260 nm vorgenom m en w ird.
In analoger W eise ist es möglich, durch E in w ir­
kung von H ydrazin nach H a b e r m a n n 2 aus DNS
A p yrim idinsäure zu erhalten, die nach A btrennung
der P yrim id in b asen in ihre P urinnucleotid-Sequenzen unterschiedlicher K ettenlänge aufgetrennt w er­
den kann. A uf G rund der G esetzm äßigkeiten der
Basenzusam m ensetzung und deren A nordnu n g in
der D N S-D oppelhelix m üssen in beiden Fällen die
gleichen Z ahlenw erte fü r die M ono- und O ligomerenN ucleotide erhalten w erden, was auch von H a b e r ­
mann
* Anschrift der Verfasser: 69 Jena, Beuthenbergstraße 11.
1 C h . T a m m , M . E. H o d e s u . E. C h a r g a f f , J . biol. Chemistry
195. 49 [1952].
2 V. H a b e r m a n n , Collect, czechoslov. chem. Commun. 26. 3147
[1961].
3 V.
4 S.
aa + aa + a + aaa + a + a + aa + . . .
Ebenso kann m an im rechten D oppelstrang A =
G = a setzen. Zur B erechnung der verschiedenen
M öglichkeiten soldier n u r aus P u rin - oder Pyrim idinbasen bestehender Sequenzketten d er DNS h at
H a b e r m a n n 3 ein einfaches m athem atisches M odell
verw endet, das eine q u an titativ e A bschätzung der
V erteilung der theoretisch zu erw arten d en H äufig­
keiten der N ucleotidsequenzen ih re r G röße nach ge­
stattet.
D as M odell b au t sich au f einer kleinen aus n
gleichartigen N ucleotiden bestehenden G run d g esam t­
heit auf, in der sich die N ucleotide au f die verschie­
denartigste W eise zu N ucleotidsequenzen u n te r­
schiedlicher Länge, 1, . . . , n, zusam m enfügen la s­
sen. Die G esam tzahl der N ucleotide säm tlicher Se­
quenzen in einer solchen G rundgesam theit m uß also
stets der konstanten G esam tzahl n entsprechen. In
dieser G rundgesam theit k an n als längste Sequenz
H aberm ann,
Nature [London] 200, 782 [1963].
u. M. C e r h o v Ä , Biophys. Biochem. Acta
H aberm annovÄ
76,310 [1963].
Dieses Werk wurde im Jahr 2013 vom Verlag Zeitschrift für Naturforschung
in Zusammenarbeit mit der Max-Planck-Gesellschaft zur Förderung der
Wissenschaften e.V. digitalisiert und unter folgender Lizenz veröffentlicht:
Creative Commons Namensnennung-Keine Bearbeitung 3.0 Deutschland
Lizenz.
This work has been digitalized and published in 2013 by Verlag Zeitschrift
für Naturforschung in cooperation with the Max Planck Society for the
Advancement of Science under a Creative Commons Attribution-NoDerivs
3.0 Germany License.
Zum 01.01.2015 ist eine Anpassung der Lizenzbedingungen (Entfall der
Creative Commons Lizenzbedingung „Keine Bearbeitung“) beabsichtigt,
um eine Nachnutzung auch im Rahmen zukünftiger wissenschaftlicher
Nutzungsformen zu ermöglichen.
On 01.01.2015 it is planned to change the License Conditions (the removal
of the Creative Commons License condition “no derivative works”). This is
to allow reuse in the area of future scientific usage.
H Ä UFIG KEITSVERTEILU NG DER SEQUENZEN UND NUCLEOTIDE
367
Native DNS
T
—
T—
—A ~
T—
—A
—
T
—
T—
—A ~
T—
—A
—
t
C
—C
—
—C ~
G—
—
G—
C
—C
—
—C ~
G—
—
G—
C—
—G ~
C—
—G
—
—T ~
A—
—
—C ~
G—
—T ~
—
-T
Weiterer
Abbau
—T
—
fr ^
A—
—
A—
A
—G ~
C—
—G
—
\~ G
—
—C ~
G—
—
—
T—
—A ~
T—
—A
—
C—
—G ~
C—
_
—T
—T
—
—
—C
+ 12 Zucker­
phosphate
G
G—
—
a
G
—
—C
T
A
A — weiterer
Abbau
G—
—C
C^9
t
A
C
+ 3A + 2A
+ 3G + 4G
H®
*—
t
Wasserstoff­
brücken
Hydrazin
G—
G
—
—
+ 4C + 3C
+ 2T + 3T
insgesamt
+ 5 A + 7G
A-
G'9
t
+ 12 Zucker­
phosphate
insgesamt
+ 5T + 7 C
Abb. 1. Schema der Apurin- bzw. Apyrimidinsäure-Bildung aus einem Teilstück einer DNS-Doppelhelix.
auch einm al, aber auch nur einm al diejenige auftreten, die aus dem Zusam menschluß säm tlicher n N u ­
cleotide der G rundgesam theit entstanden ist.
Die A ufgabe besteht nun darin, festzustellen
1. W ieviele solcher A nordnungen bei gegebener A n­
zahl n der N ucleotide a überhaupt möglich sind,
2. wieviele solcher Sequenzen der verschiedenen
Cluster-Typen in allen diesen A nordnungen en t­
halten sind und
3. wie sich diese Sequenzen und die in ihnen en t­
haltenen N ucleotide prozentual auf die einzelnen
Sequenztypen verteilen.
Es handelt sich hier um das bereits von L. E u l e r
(1 6 7 4 ), N e t t o 5 und R i o r d a n 6 behandelte kom bi­
natorische Problem , eine beliebige ganze Zahl n au f
alle möglichen A rten in ganzzahlige Sum m anden zu
zerlegen, wobei deren Reihenfolge au ß er Betracht
bleiben soll und gleichgroße Sum m anden auch m e h r­
fach Vorkommen können. Eine solche Z usam m en­
stellung additiver Z ahlengruppen m it k onstanter
Sum m e n bezeichnet m an in der K om binatorik als
vollständige P a rtitio n (m it W iederholungen) und
ih re S um m anden als Teile der P artitio n , n w ird
auch die zerlegbare Zahl d er P artitio n genannt. Ih r
entspricht in dem M odell von H a b e r m a n n die Länge
der aus n N ucleotiden bestehenden „G ru n d ein h eit“
des D N S-Fadenm oleküls. Den Teilen der P artitio n ,
also den ganzen Z ahlen von 1 bis n, entsprechen in
diesem M odell die verschieden langen Sequenzen
aus 1 bis n gleichartigen N ucleotiden. Die H ochzah­
len bedeuten h ier die A nzahl der gleichartigen N u ­
cleotide in n erh alb ein er Sequenz und entsprechen
den ganzen Z ahlen in der P artitio n .
F ü r die G esam tzahl p (n ) aller vollständigen P a r ­
titionen der ganzen Zahlen n gibt es um fangreiche
Tafeln, die diese W erte fü r alle natürlichen Zahlen
von 1 bis 6 0 0 en th alten ( G u p t a 7 ) . B isher gibt es
jedoch noch keine T afeln für die Anzahl bzw. H äu ­
figkeiten der S equenzen innerhalb säm tlicher P a rti­
tionen der Z ahlen n. Diesem M angel soll m it den
in dieser A rbeit berechneten Tabellen abgeholfen
w erden.
5 E.
7 H.
N e t t o , Lehrbuch der Combinatorik, B. G . Teubner, Leipzig 1901.
6 J. R io r d a n , An Introduction to Combinatorical Analysis,
John Wiley a. Sons, New York 1958.
G u p t a , Proc. London mathem. Society 2. Ser. 39, 142
[1935] ; H. G u p t a , Proc. London mathem. Society 2. Ser.
42,546 [1937].
368
H. PO SSNER UND H. GRIM M
F ü r kleine Zahlen n, etwa bis n = 8, lassen sich
die H äufigkeiten der einzelnen Sequenztypen durch
A ufstellung der einzelnen Z erlegungen (für n = 8
sind es 22 M öglichkeiten) und A bzählen der Ziffern
(Sequenzen) 1, 2, 3, . . . , 8 leicht bestim m en. A ber
bereits fü r n = 1 3 ist dieses V erfahren schon eine
recht zeitraubende Angelegenheit. Es m üßten in die­
sem Falle 101 P artitionen aufgestellt und nach den
verschiedenen Ziffern ausgezählt w erden. F ü r n = 25
sind es bereits nahezu 2000 P artitio n en und für
n = 100 über 190 M illionen P artitio n en .
A us dem G u p t a sehen Z ahlenm aterial für p ( n )
lassen sich jedoch durch ein einfaches A dditio n sv er­
fah ren die H äufigkeiten säm tlicher Sequenzen au f­
bauen, ohne erst die ganze Reihe der Zerlegungen
durchführen zu müssen.
Diese Berechnung ist ein stufenw eises R ekursio n s­
verfahren, das m it der niedrigsten Sequenz a b e­
gin n t und Schritt für Schritt bis zur höchsten Se­
quenz a” weitergeht.
Die Sequenz a tritt näm lich zunächst beim erst­
m aligen A btrennen einer Sequenz a von der ganzen
K ette n, also so oft auf, wie die G esam tzahl der P a r ­
titionen fü r (n — 1) beträgt, also p {n — l)-m a l.
Die Sequenz a tritt w eiterhin beim nochm aligen
A btrennen einer Sequenz a von der bereits um ein
N ucleotid gekürzten Kette n — 1 und zw ar so oft auf,
wie der Gesamtzahl der P artitio n en fü r (n — 2) en t­
spricht, also p (n —2 ) -mal.
D ieser G edankenversuch des stückw eisen A b tren ­
nens w ird nun solange fortgesetzt, bis die K ette au f­
gebraucht ist, also so lange, bis der letzte T erm p (0 )
der fallenden Reihe p {n — 1 ), p {n — 2 ) , p {n — 3 ) ,
. . . , p ( l ) , p ( 0 ) , erreicht bzw. unterschritten w ird.
Die Sequenz a tritt also innerhalb aller P artitio n en
der Zahl n so oft auf, wie die Sum m e der folgenden
R eihe der P artitionszahlen b eträ g t: H äufigkeit der
Sequenz a 1 = p ( n — 1) + p ( n —2) + p (n —3) + • • •
. . . + p ( l ) + p ( 0 ) . H ierbei w ird definitionsgem äß
die A nzahl p (0 ) der P artitionen der Z ahl 0 gleich 1
und die A nzahl der P artitionen für negative Zahlen
gleich 0 gesetzt.
Ganz entsprechend erhält m an durch sukzessives
A btrennen der Sequenz a 2 für die H äufigkeit der
Sequenz a 2 innerhalb säm tlicher P artitio n en der
Zahl n die folgende Summe der jew eils um das A r­
gum ent 2 fallenden P artitionsfunktionen. H äufigkeit
von a 2 = p (n —2) + p (n —4) + p ( n —6) + . . . Bei
der Summe für die H äufigkeit der Sequenz a 3 fällt
das A rgum ent der P artitio n sfu n k tio n jew eils um
den W ert 3 und es ergibt sich fü r die
H äufigkeit der Sequenz
a 3 = p (n - 3) + p ( n —6) + p { n - 9) + . . .
H äufigkeit der Sequenz
a4 = p ( n - 4) + p ( n - 8) + p (n - 12) + . . .
Die S um m ierung w ird in der fallenden R eihe der
p ( n ) jew eils solange fortgesetzt, bis der E ndw ert
p ( 0 ) d er R eihe unterschritten ist.
Die allgem eine Form el fü r die H äufigkeit sn der
Sequenz a' ( i = l , . . . , n ) in der G rundkette der
L änge n lautet d em nach:
■Sn(a')
wobei
'Z p ( n - h i ) ,
h= l
die kleinste Zahl des Quotienten
(1)
ist.
W erden auf diese W eise die H äufigkeiten fü r
säm tliche Sequenztypen von 1 bis n aufgestellt, und
die einzelnen H äufigkeitszahlen m it der A nzahl i der
in der jew eiligen Sequenz enthaltenen N ucleotide
m ultipliziert, so m uß die A ufsum m ierung der P ro ­
dukte fü r alle Sequenztypen 1 bis n die Gesamtzahl
säm tlicher N ucleotide eines Fadens der abgebauten
D oppelhelix ergeben. Diese Gesamtzahl setzt sich
aus p { n ) P artitio n en m it der jeweils gleichen Nucleotidanzahl n der G rundgesam theit zusam m en und
m uß d ah er den bei gegebener Zahl n festliegenden
W ert n p ( n ) besitzen. D ieser W ert w urde fü r die
jew eilige V erteilung der Sequenzen als K ontrolle
verw endet. A us Form el (1) erhält m an durch Sum ­
m ierung der sH(al)-W erte ü ber alle Sequenzen 1 bis
n u n ter M ultiplikation m it dem jew eiligen z’-W ert
folgende Form el (2) :
(2)
B eispiel fü r n = 13
M an entnim m t der G u p t a sehen Tafel, oder
auch dem Lehrbuch von R i o r d a n 6 (S. 122) die
W erte fü r die P artitio n sfu n k tio n für n = 13, 12, 11,
10, . . . , 1, 0 in fallender Reihenfolge (Tab. 1 ).
U nter A nw endung der F orm eln (1) und (2) e r­
g ib t sich d an n die T ab. 2 fü r die G rundgesam theit
n = 13. F ü r n = 13 b eträg t die Gesamtzahl aller N u­
cleotide in säm tlichen Sequenzen n 'p { n ) = 13■ 101
= 1313.
H Ä U FIG K E ITSV E R TE ILU N G DER SEQUENZEN UND NUCLEOTIDE
» —1
n —2
n —3
13
12
11
10
9
p (n ) 101
77
56
42
30
n
n —5
n —4
n —6
369
n — 10 » - 1 1 n — 12 n — 13
n - 7
n —8
n —9
8
7
6
5
4
3
2
1
0
22
15
11
5
3
2
1
1
7
Tab. 1. Werte für die Partitonsfunktion für n in fallender Reihenfolge.
Sequenztyp
(al)
Anzahl der
Sequenzen
i
sn (a*)
Rel. Sequenzhäufigkeit (%)
100
Rel. Nucleotidhäufigkeit [%]
100 i sn (a *)
Anzahl der
Nucleotide
sn(a*)
i Sniat)
n ■p (n )
2 «n(as)
(aus Tab. 3)
1
2
272
3
4
5
63
38
25
6
16
7
8
9
10
11
12
13
Summe
112
11
7
5
3
2
1
1
556
46
i= l
(aus Tab. 4)
(aus Tab. 5)
1 272 = 272
2 112 = 224
48,92
20,14
11,33
6,83
4,50
3
4
5
2 ,8 8
6
1,98
1,26
0,90
0,54
0,36
0,18
0,18
7
8
8,27
100
9
10
11
12
13
63 =
38 =
25 =
16=
11=
7=
5=
3=
2 =
1=
1=
189
152
125
96
77
56
45
30
22
12
13 J
1313
351
20,72
17,06
14,39
11,58
9,52
7,31
5,86
4,27
3,43
2,28
26,73
1,68
0,91
0,99
100
Tab. 2. Absolute und relative Häufigkeiten der Sequenzen und Nucleotide für n = 13.
Abb. 2. Sequenz-Häufigkeiten (n = Maximal-Sequenz der jeweiligen D NS).
Abb. 3. Nucleotid-Häufigkeiten (/i=Maximal-Sequenz der
jeweiligen DNS).
370
H. POSSNER UND H. GRIM M
§ g
'S
O 03)
E- S
"O •—
0)
1-6
3 m
S
_rj4>J1r—
/5I ^3
<D.2
‘S ^
N B
5 C
»
<"
csß
u3 —
;
5
2 N
’S ’S
£ N
r- GW
5 .a
3 O.
trc/j
Nach vorliegendem R ek u rsio n sv erfah ren w urden
die in den T abellen 3, 4 u n d 5 zusam m engestellten
H äufigkeiten d er Sequenztypen u n d der in ihnen
enthaltenen N ucleotide fü r n = 1 ( 1 ) 2 7 bzw. n — 3,
5 ( 3 ) 2 7 , 50, 100, 600 berechnet. F ü r den g rößten
W ert von n = 6 0 0 w urden die bis auf 24 Stellen
ansteigenden W erte der P artitio n sfu n k tio n p ( n ) aus
den G u p t a sehen Tafeln au f 3 gültige Ziffern re d u ­
ziert und so die H äufigkeit der Sequenzen a 1 bis a 127
berechnet. T rotz dieses abgekürzten V erfahrens b lie­
ben die F eh ler fü r die prozentuellen H äufigkeiten
der einzelnen Sequenzen g ering, und es ergab sich
n u r ein Defizit von etwa 6%0 vom Sollw ert n 'p ( n )
der Gesam tzahl d er N ucleotide.
D ie A bbn. 2 u n d 3 zeigen die in den T abn. 4
und 5 enthaltenen H äufigkeitsverteilungen der Se­
quenztypen a 1 b is a 10 fü r verschiedene D N S-Typen
m it den M axim alsequenzen n = 3, 5, 8, 11, 14, 17,
20, 23, 27, 5 0 , 100, 600. A uf der horizontalen
Achse sind die Sequenztypen in logarithm ischem
M aßstab u n d a u f d er vertikalen Achse die relativen
H äufigkeiten in P rozenten abgetragen.
W enn nun die K urve der experim entellen W erte
fü r die S equenzhäufigkeiten m it ein er der th eo reti­
schen K urven fü r einen bestim m ten W ert von n zur
D eckung gebracht w erden kan n , so bedeutet dies,
daß die längsten in diesem DN S-M olekül v o rk o m ­
m enden P u rin - o d er P yrim idinsequenzen von n Nucleotiden gebildet w erden. E in solcher T eilfaden von
n N ucleotiden w u rd e oben als „G ru n d ein h eit“ b e­
zeichnet und d er gesam ten H äufigkeitsberechnung
zugrunde gelegt. D ie G esam theit säm tlicher N ucleo­
tide in einem S tran g e des D N S-M oleküls besitzt nach
obiger B etrachtung den W ert n mp { n ) N ucleotide.
D a diese G röße jedoch n u r die Basen zählt und
außerdem das ganze D N S-M olekül aus einer D o p ­
pelhelix, d. h. aus zwei S trängen besteht, so besitzt
aus G ründen der Sym m etrie das ganze D NS-M ole­
kül 4 n - p ( n ) N ucleotide. W ird das Mol.-Gew. eines
N ucleotids zu 3 0 8 gerechnet, so läß t sich ganz all­
gem ein als F o rm el fü r das Mol.-Gew. einer doppelsträn g ig en DNS d er W ert 4 n ' p ( n ) -3 08 = 1232
n - p ( n ) angeben, wo n die längste in der betreffen­
den DNS vorkom m ende N ucleotidsequenz (NucleotidCluster) bedeutet. T ab. 6 en thält die zu den W erten
von 7i = l ,
...,
30 gehörenden Mol.-Gew. einer
doppelsträngigen D N S.
H Ä U FIG K EITSV ERTEILU N G DER SEQUENZEN UND NUCLEOTIDE
371
n
Sequenz-
3
5
8
11
14
17
20
23
27
50
66,67
16,67
16,67
60 00
20,00
10,00
5,00
5,00
52,33
22,09
10,47
6,98
3,49
2,33
1,16
1,16
50,54
20,36
11,27
6,54
4,36
2755
1,82
1,09
0,73
0,36
0,36
47,82
20,51
11,15
7,05
4,49
3,08
2,05
1,41
0,90
0,64
0,38
0,26
0,13
0,13
46,56
19,80
11,30
7,07
4,78
3,21
2,29
1,58
1,12
0,76
0,56
0,36
0,25
0,15
0,10
0,05
0,05
45,08
19,68
11,21
7,26
4,88
44,17
19,28
11,23
7,25
5,01
3,53
2,58
1,87
1,39
1,02
0,76
0,55
0,41
0,29
0,22
0,15
0,11
0,07
0,05
0,03
0,02
0,01
0,01
42,98
18,98
11,17
7,31
5,10
3,67
2,71
2,01
1,52
1,14
0,87
0,66
0,50
0,37
0,28
0,21
0,15
0,11
0,08
0,05
0,04
0,03
0,02
0,01
0,01
0,00
0,00
38,92
17,79
10,81
7,37
5,34
4,02
3,10
2,44
1,94
1,55
1,26
1,02
0,83
0,68
0,55
0,45
0,37
0,30
0,25
0,20
0,16
0,13
0,11
0,09
0,07
0,06
0,04
0,04
0,03
0,02
100
600
\
Typ i
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
3743
2,42
1,77
1,25
0,93
0,65^
0,48
0,32
0,24
0,15
0,11
0,06
0.04
0,02
0,02
Iz T
22
23
24
25
26
27
28
29
30
Tab. 4. Sequenzhäufigkeiten =
35,04
16,44
10,27
7,21
5,39
4,19
3,34
2,72
2,25
1,88
1,58
1,34
1,14
0,98
0,84
0,72
0,62
0,54
0,47
0,41
“ 0,35
0,31
0,27
0,23
0,20
0,17
0,15
0,13
0,11
0,10
27,48
13,39
8,70
6,35
4,94
4,01
3,35
2,84
2,47
2,15
1,90
1,70
1,52
1,38
1,24
1,13
1,04
0,95
0,87
0,80
0,74
0,69
0,64
0,59
0,55
0,51
0,48
0,45
0,42
0,39
100 Sn (a1)
~
—-----------(in %).
£ sn(a‘)
t= l
F ü r die von H a b e r m a n n 3, als auch von S e d a t
und S i n s h e i m e r 8 untersuchte zw eisträngige KalbsT hym us-D N S ergab sich beim V ergleich der Se­
quenzhäufigkeiten m it den theoretischen W erten
eine günstige A npassung an die theoretische
K urve fü r eine M axim alsequenz von n = 13 Nucleotiden. Nach der Z usam m enstellung in T ab. 2 erge­
ben sich fü r diesen F all insgesam t 5 5 6 Sequenzen.
Diese enthalten nach obiger F orm el n 'p ( n ) =
1 3 p ( 1 3 ) = 1 3 1 3 N ucleotide, da fü r n = 13 die Ge­
sam tzahl aller m öglichen P artitio n en p (13) = 1 0 1
b eträgt. D em nach enthält ein M olekül ein er solchen,
von diesen A utoren zu r U ntersuchung verw endeten,
DNS insgesam t 5252 N ucleotide. Es m uß daher ein
Mol.-Gew. von 1,6 M illionen besessen haben (s.
T ab. 6 ) .
Das Mol.-Gew. kan n som it als F unk tio n des M axi­
m alw ertes n der Polynucleotidketten der jew eiligen
8 I. S edat
[1 9 6 4 ].
u
.
R. L.
S in s h e im e r ,
J. molecular Biol. 9,
489
DNS abgeschätzt w erden. F ü r die von S e d a t und
untersuchte P hagen-D N S
174, die
einsträngig ist, trifft die V oraussetzung fü r kom ple­
m entäre Z u ordnung der N ucleotide nicht m ehr zu,
u n d es treten auch erhebliche A bw eichungen von der
theoretischen V erteilung fü r n = 13 auf.
S in s h e im e r 8
Nach Abschluß dieser Arbeit wurde uns noch eine
Veröffentlichung von S h a p ir o und M itarbb. 9 über die
Verteilung der Pyrimidin-Sequenzen in Desoxyribonucleinsäuren bekannt. Bei S h a p ir o werden zur Anpas­
sung an die experimentelle Häufigkeitsverteilung der
Nucleotid-Sequenzen Exponentialkurven verwendet, die
von N atur aus stetig sind, während in der hier vorlie­
genden Berechnungsweise der diskrete Charakter der
Nucleotidverteilung berücksichtigt wird.
Wir danken H errn Dr. habil H. V e n n e r für die An­
regung zu dieser Arbeit und die wertvollen Hinweise
zum biochemischen Teil.
9 H.
S . S h a p i r o , R . R u d n e r , K. I. M
ture [London] 205, 1068 [1965].
iu r a
u
.
E.
C harga ff,
Na­
372
HÄ U FIG K EITSV ERTEILU N G DER SEQUENZEN UND NU CLEOTIDE
n
SequenzTyp i
\ .
..\
3
5
8
25,57
21,59
15.34
13.64
8,52
1
2
44,44
34,29
22,22
22,86
3
4
5
33,33
6
7
8
9
10
11
12
11
22.56
18,18
17,14
15.09
11,43
11,69
14,29
9,74
~6,82~ 6,82
3,98
5,68
4,55
3,90
2,92
1,62
1,79
13
14
15
16
17
18
19
14
17
20
23
27
50
19,74
16,93
13,81
11,64
9,26
7,62
5,93
4.66
3,33
2,65
1,75
1,27
0,69
0,74
18,12
15,41
13,19
1,66
2,11
1,29
0,83
0,59
0,32
0,34
1,56
1,23
0,84
0.64
0,41
0,29
0,15
0,16
15,62
13,64
11.91
10,25
8,85
~^48"
6,38
5,29
4,43
3,60
2.97
2,33
1,89
1,46
1,14
0.83
0,65
0,44
0,33
14,44
12,75
11,26
9,82
8,57
7,39
6,37
5,40
4,61
3,84
3^22
2,64
2,18
1,74
1,42
10,69
9,77
8,91
9,31
7^49
6,24
4,91
3,92
2,97
2,40
16,64
14,53
12,42
10,72
9,01
7^61
6,25
5,23
4,16
3,43
2,63
11,01
20
0,21
0,15
0,08
0,08
21
22
23
24
25
26
27
28
29
30
0,06
0,03
0,03
1,10
0,88
0,66
0,51
0,37
0,28
0,19
0,14
0,09
0,33
j
7,33
6,63
5,96 1
5,35
4,79
4,27
3,79
3,36
2,96
2,61
2,28
1,99
1,73
1,50
1,29
8 ,10
Tab. 5. Nucleotidhäufigkeiten =
np{n)
— (in %).
« M C C O O N O N O O N C O f f l O O N O O O N N T f K O ' f O I N O M O O
M N X ^ I N - i O J J ' f ^ r t O ' H X X t ' O a J ’- H t ' N O O O C O i O T f f N N ' #
( N S O O r - i C O C C X C C - ^ C 5 C O C O ' < t ' > # - ^ C O C ^ f O C C i C C < N < ^ 5 0 - ^ a i C C ’- ^ f C i C C
-H N T)iXF(N
^n'-'lO m rt(N »0>O N «N iO ffllO O t'0(M lN iS05(M
H ( N M l O t ' H t D C O I M > n N l O - ^ ' > i < T ) l H l O l C C O O ^ N O ' H
HHi MM' l t EOOHLOOt ' l Of f l OMOWn t '
HH(M«n^ct'0N00
■ ^ ONOCi O
Ot'M
C ONOHf fMl ^H«ffi^C
O O O5'<
f f i)(ei5
OOO
N ' '#
#C
^ iXO(N
O
O®
tOiO
H (^M
®O
OO
lOO«O
t'O
H H N ^ e ® M
* ® ® O f f l W
W
5 f f l O X O O ® M N H C i 5 H
H HC^ « l ! 5 ®®H®( NQ0 t ' XMHi J ( NX
h h NNCO^®XO«®
O
600
7,62
7.15
6,70
6,27
5,86
5,46
5,09
4,74
4.40
4.08
3,78
3,49
3,22
2,97
2,73
2,51
2,31
3,15
3.07
2,99
2,91
2.83
2,76
2,68
2,61
2,54
2,46
2^40
0,22
0,80
0,72
0,65
2.33
2,27
2,21
2,14
2.07
2,02
1,97
1,90
1.84
1/79
1,73
1,67
1,63
1,57
1,53
1,48
1,44
1,39
1.34
0,71
4,98
35,28
1,11
0.94
0,80
0,6 8
0,57
0,48
0,40
0,89
0,27
0,18
Längere
Sequenzen
100
2,11
1,93
1,85
1.61
1,46
1,33
1,21
1,09
0,99