Bipartite Graphen Beispiele

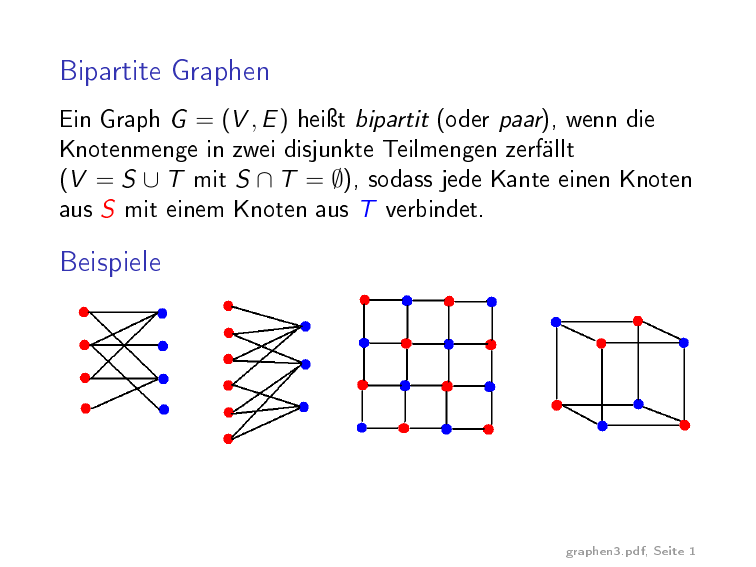
Bipartite Graphen
Ein Graph
G = (V , E ) heiÿt bipartit (oder paar), wenn die
Knotenmenge in zwei disjunkte Teilmengen zerfällt
V = S ∪ T mit S ∩ T = ∅), sodass jede Kante einen Knoten
aus S mit einem Knoten aus T verbindet.
(
Beispiele
graphen3.pdf, Seite 1
Eigenschaften
I Ein Graph ist genau dann bipartit, wenn es keinen aus
einer ungeraden Anzahl von Kanten bestehenden
geschlossenen Weg gibt.
I Bei einem zusammenhängenden bipartiten Graphen ist die
V = S ∪ T eindeutig bestimmt.
Ist G = (V , E ) bipartit mit V = S ∪ T , so gilt:
Zerlegung
I
Bei einem aus einer geraden Anzahl von Kanten
bestehenden Weg gehören Start- und Endpunkt zur
selben Menge
S
oder
T , bei einem aus einer ungeraden
Anzahl von Kanten bestehenden Weg gehören Start- und
Endpunkt zu verschiedenen Mengen.
graphen3.pdf, Seite 2
Konstuktion einer Zerlegung V = S ∪ T
durch Markierung der Knoten eines zusammenhängenden
(ungerichteten) Graphen:
1. Markiere einen (beliebigen) Startknoten mit
s.
2. Markiere alle Nachbarknoten des Startknotens mit
t.
3. Markiere alle noch unmarkierten Knoten, die einen mit
markierten Nachbarknoten haben, mit
unmarkierten Knoten, die einen mit
Nachbarknoten haben, mit
t.
s
t
s , sowie alle noch
markierten
4. Wiederhole Schritt 3 so lange, bis entweder
I alle Knoten markiert sind oder
I zwei benachbarte Knoten die gleiche Markierung haben.
In diesem Fall ist der Graph nicht bipartit und der
Algorithmus kann abgebrochen werden.
graphen3.pdf, Seite 3
Matchings
Sei
G = (V , E ) bipartit mit V = S ∪ T .
I Ein
Matching (oder Paarung) ist eine Teilmange E0 ⊂ E
der Kantenmenge, so dass jeder Knoten mit maximal
einer Kante aus
E0
inzident ist.
I Ein Matching heiÿt maximal, wenn es kein anderes
Matching gibt, das mehr Kanten enthält.
vollständige Paarung ist ein Matching E0 , so dass
jeder Knoten mit einer Kante aus E0 inzident ist.
I Eine
Matchings E
0
graphen3.pdf, Seite 4
Eigenschaften und Bemerkungen
I Jeder bipartite Graph hat ein maximales Matching. Dieses
ist i. a. nicht eindeutig.
I Nicht jeder bipartite Graph hat eine vollständige Paarung.
I Jede vollständige Paarung ist ein maximales Matching.
E0 deniert eine bijektive
S → T , wenn man jedem
Element s ∈ S das (eindeutige) Element von T zuordnet,
das mit s durch eine Kante aus E0 verbunden ist.
I Eine vollständige Paarung
Abbildung (1:1Zuordnung)
Insbesondere ist eine vollständige Paarung nur möglich,
wenn
S
und
T
gleich viele Elemente haben.
Aber auch in diesem Fall ist die Existenz einer
vollständigen Paarung nicht garantiert.
graphen3.pdf, Seite 5
Konstruktion maximaler Matchings
über
augmentierende Wege (ungarischer Algorithmus,
Algorithmus von Hopcroft und Karp)
Augmentierender Weg
G = (V , E ) mit V = S ∪ T
E0 .
Ein augmentierender Weg (erweiternder Weg;
Verbesserungsweg) ist ein Weg in G mit folgenden
Gegeben sei ein bipartiter Graph
und ein (beliebiges) Matching
Eigenschaften:
ungepaarte Knoten, d. h. sie
sind mit keiner Kante aus E0 inzident,
I Start- und Endknoten sind
I Die Kanten des des Weges gehören abwechselnd zu
E \ E0
und zu
E0
(der Weg ist
alternierend).
graphen3.pdf, Seite 6
Beispiel
Ein augmentierender Weg führt zur Verbesserung eines
gegebenen Matchings
E0 , indem die zu E0
gehörenden Kanten
des Weges aus dem Matching entfernt und die nicht zu
E0
stattdessen hinzugefügt werden (Umschalten des Weges).
Das neue Matching enthält eine Kante mehr als das alte, da
die erste und letzte Kante des augmentierenden Weges nicht
zu
E0
gehören.
graphen3.pdf, Seite 7
Bemerkung
Jeder augmentierende Weg besteht aus einer ungeraden
Anzahl von Kanten, da er alterniernend ist und die erste und
die letzte Kante nicht zum Matching gehören.
Damit liegt entweder der Startpunkt in
T
S
und der Endpunkt in
oder umgekehrt.
Es genügt dabei, augmentierende Wege zu betrachten, die in
einem ungepaarten Knoten aus
ungepaarten Knoten aus
T
S
beginnen und in einem
enden.
graphen3.pdf, Seite 8
Der Ungarische Algorithmus
beruht auf dem
E0
Satz: Ein Matching
ist genau dann maximal, wenn es
keinen augmentierenden Weg gibt. Damit
1. Starte mit einem bekannten Matching
E0
(z. B.
E0 = ∅).
2. Suche einen augmentierenden Weg.
I Gibt es einen augmentierenden Weg, so ersetzte das
aktuelle Matching
E
n
+1
E
n
durch ein neues besseres Matching
durch Umschalten entlang des Weges.
Formal: Ist
A die Menge der zum augmentierenden Weg
gehörenden Kanten, so setze
E
n
+1
= E ∆ A = (E \ A) ∪ (A \ E ).
n
n
n
I Gibt es keinen augmentierenden Weg, so ist das aktuelle
Matching
E
n
maximal.
3. Wiederhole Schritt 2, so lange es augmentierende Wege
gibt.
graphen3.pdf, Seite 9
Finden eines augmentierenden Weges
durch Markierung der Knoten oder (äquivalent) Betrachten
eines gerichteten Graphen:
Die zum aktuellen Matching
die Richtung von
von
S
nach
T
T
nach
S
E
n
gehörenden Kanten bekommen
(von rechts nach links), die übrigen
(von links nach rechts). Ein augmentierender
Weg ist dann ein gerichteter Weg, dessen Startpunkt (in
und Endpunkt (in
T ) in E
n
S)
ungepaarte Knoten sind. Dieser
kann z. B. durch eine Breitensuche gefunden werden.
graphen3.pdf, Seite 10
Bemerkungen
I Ist
n
die Zahl der Knoten und
m
die Zahl der Kanten, so
hat der ungarische Algorithmus die Komplexität
O (n · m) = O (n3 ).
I Beim Algorithmus von Hopcroft und Karp werden
simultan mehrere augmentierende Wege betrachtet. Dies
führt zu einer Verbesserung der Komplexität auf
√
O ( n · m) = O (n ).
5
2
I Der ungarische Algorithmuis berechnet simultan zum
maximalen Matching eine
minimale Knotenüberdeckung
(duales Problem).
I Man kann Paarungen auch in nicht bipartiten Graphen
betrachen. Auch hier kann eine maximale Paarung über
augmentierende alternierende Wege gefunden werden.
graphen3.pdf, Seite 11
Beispiel
Gesucht ist ein maximales Matching im bipartiten Graphen
G = (S ∪ T , E ) mit S = {1, 2, 3, 4}, T = {a, b, c , d } und
E = {1a, 1c , 2a, 2b, 2d , 3a, 3c , 3d , 4c }.
Als Startpunkt für den ungarischen Algorithmus kann das
E0 = ∅ genommen werden.
Dann bildet jede Kante aus V einen augmentierenden Weg der
triviale Matching
Länge 1, d. h. es gibt die augmentierenden Wege
a c
a b d
a c
1 , 1 , 2 , 2 , 2 , 3 , 3 , 3
d
c
und 4 .
graphen3.pdf, Seite 12
Beispiel: Übergang E → E
0
von links: Graph mit Matching
1
E0 = ∅, zugehöriger gerichteter
Graph mit möglichen Anfangs- und Endpunkten
augmentierender Wege, ausgewählter augmentierender Weg
a
2 , Matching
E1 = {2a} nach Umschalten.
graphen3.pdf, Seite 13
Beispiel: Übergang E → E
1
Zu
E1
2
gibt es noch augmentierende Wege der Länge 1, d. h. es
können Kanten hinzugefügt werden, ohne andere aus dem
c
c und 4c .
Mit Auswahl von 3c erhält man E2 = {2a, 3c }.
Matching herauszunehmen: 1 , 3
graphen3.pdf, Seite 14
Beispiel: Übergang E → E
2
3
Jetzt lässt sich keine Kante mehr direkt hinzufügen,
augmentierende Wege haben mindestens die Länge 3. Es gibt
folgende Möglichkeiten:
a b a d c a b c a d c a b (ausgewählt) und
c a d
E3 = E2 ∪ {4c , 3a, 2b} \ {2a, 3c } = {4c , 3a, 2b}.
1 2 , 1 2 , 1 3 2 , 1 3 2 , 4 3 2
4 3 2 . Umschalten liefert ein neues Matching
graphen3.pdf, Seite 15
Ende des Algorithmus
Jetzt gibt es keine augmentierenden Wege mehr. Jeder
Versuch, einen solchen (der im Knoten 1 beginnen muss) zu
a c
c
bilden, endet in der Sackgasse 4: 1 3 4, 1 4.
Somit ist das Matching
E3
maximal. Insbesondere gibt es keine
vollständige Paarung.
Bemerkung: Das maximale Matching ist nicht eindeutig,
sondern das Ergebnis hängt von der Auswahl der
augmentierenden Wege in den einzelnen Teilschritten ab.
graphen3.pdf, Seite 16
Netzwerke
Ein Netzwerk ist ein zusammenhängender, gerichteter und
G = (V , E ) mit Gewichten g (i , j ) > 0 mit
Knoten: Quelle q ∈ V und Senke s ∈ V .
gewichteter Graph
zwei speziellen
graphen3.pdf, Seite 17
Anwendungen
I Datennetze
I Leitungsnetze (Wasser, Gas, ...)
I Verkehrsplanung
Die Gewichte werden dabei als (Transport-)Kapazitäten
interpretiert.
Ziel ist, möglichst viel von der Quelle zur Senke zu
transportieren.
Der Transport wird durch
zulässige Flüsse beschrieben.
graphen3.pdf, Seite 18
Flüsse in einem Netzwerk
Ein zulässiger Fluss ist eine Abbildung
I 0
≤ f (i , j ) ≤ g (i , j )
f : E → R mit
für jede Kante
(i , j ) ∈ E
(die durch die Kante transportierte Menge übersteigt
nicht deren Kapazität),
I Für jeden Knoten
P
i
f (i , j ) =
P
k
j
mit
j 6= q
und
j 6= s
ist
f (j , k ), d. h. die Summe der Flüsse
über alle in den Knoten j hineinzeigenden Kanten ist
gleich der Summe über die aus j herauszeigenden Kanten
(
Kirchhosches Gesetz, die Gesamtmenge des in den Knoten
hinein transportierten Flusses ist gleich der Gesamtmenge des
aus dem Knoten heraus transportierten Flusses).
graphen3.pdf, Seite 19
Gesamtuss
Der
Gesamtuss oder Wert des Flusses ist gegeben durch
X
f (q , j ) =
X
j
(Gesamtmenge, die von
Ein Fluss ist
f (i , s )
i
q
nach
s
transportiert wird).
maximal, wenn sein Gesamtuss so groÿ wie
möglich ist.
graphen3.pdf, Seite 20
Beispiel: Fluss mit Wert 4
Die blauen Zahlen geben den Fluss der jeweiligen Kanten an.
Der Gesamtuss
F
ist die Summe aller Flüsse, die aus der
Quelle herauskommen bzw. in die Senke hineinlaufen:
F = f (q , a) + f (q , b) = 1 + 3 = 4 = 3 + 1 = f (c , s ) + f (d , s ).
graphen3.pdf, Seite 21
Konstruktion von maximalen Flüssen
Naiver Ansatz, Teil 1: Finde einen (gerichteten) Weg von
q
nach
s
und ordne allen Kanten entlang des Weges den
gleichen Fluss zu, der sich nach der Kante mit der geringsten
Kapazität richtet. Die übrigen Kanten des Netzwerks
bekommen Fluss 0.
graphen3.pdf, Seite 22
Konstruktion von maximalen Flüssen
Naiver Ansatz, Teil 2: Suche einen weiteren Weg von
s über noch nicht benutzte Kanten (i , j ) mit Fluss
f (i , j ) = 0 und transportiere gröÿtmögliche Menge über
q
nach
diesen Weg.
graphen3.pdf, Seite 23
Konstruktion von maximalen Flüssen
Naiver Ansatz, Teil 3: Gibt es keine unbenutzten Wege
mehr, so suche einen Weg von
ausgelastete Kanten
(i , j )
mit
q nach s über noch nicht voll
f (i , j ) < g (i , j ). Vergröÿere
den Fluss entlang des Weges so weit wie möglich.
graphen3.pdf, Seite 24
Ende des naiven Ansatzes
Jetzt führt jeder Weg von
q
nach
s
über mindestens eine voll
ausgelastete Kante.
Bedeutet dies, dass keine Verbesserung mehr möglich und der
Fluss maximal ist?
graphen3.pdf, Seite 25
Nein!
Weitere Verbesserung über
augmentierende Wege möglich!
graphen3.pdf, Seite 26
Ein augmentierender Weg
ist ein Pfad von
q
nach
s , bei dem Kanten auch in der
falschen Richtung benutzt werden dürfen, wobei:
I Ist
(i , j )
eine Kante des augmentierenden Weges, die in
der richtigen Richtung benutzt wird, so gilt
I Ist
(j , i )
f (i , j ) < g (i , j ).
eine in der falschen Richtung durchlaufene
Kante mit
(i , j ) ∈ E ,
so gilt
f (i , j ) > 0.
graphen3.pdf, Seite 27
Auswerten des augmentierenden Weges
Wähle
I
I
k > 0 so groÿ wie möglich, so dass
f (i , j ) + k ≤ g (i , j ) für alle Vorwärtskanten des Weges.
f (i , j ) ≥ k für alle Rückwärtskanten (j , i ) des Weges.
Dann entsteht ein neuer besserer zulässiger Fluss, indem der
Fluss der Vorwärtskanten um
Rückwärtskanten um
k
k
erhöht und der der
erniedrigt wird (im Beispiel ist
k = 1).
graphen3.pdf, Seite 28
Bemerkung
Die im naiven Ansatz betrachteten Wege sind Spezialfälle
von augmentierenden Wegen, nämlich solche ohne
Rückwärtskanten.
Algorithmus von Ford-Fulkerson
zur Bestimmung eines maximalen Flusses:
1. Starte mit bekanntem zulässigen Fluss
(z. B.
f (i , j ) = 0 für alle Kanten)
2. Suche augemtierenden Weg. Existiert ein solcher, ändere
den Fluss entsprechend. Existiert kein augmentierender
Weg, so ist der aktuelle Fluss maximal.
3. Wiederhole Schritt 2, solange augmentierende Wege
existieren.
graphen3.pdf, Seite 29
Aunden eines augmentierenden Weges
durch Markierung der Knoten
oder durch Betrachten eines gerichteten Graphen
G̃ = (V , Ẽ )
mit
I
I
(i , j ) ∈ Ẽ ,
(j , i ) ∈ Ẽ ,
falls
falls
(i , j ) ∈ E
(i , j ) ∈ E
f (i , j ) < g (i , j ),
und f (i , j ) > 0,
und
G̃ ihre Richtung, voll
ausgelastete Kanten mit f (i , j ) = g (i , j ) kehren die Richtung
um und teilweise ausgelastete Kanten sind in G̃ in beiden
d. h. Kanten mit Fluss 0 behalten in
Richtungen vorhanden.
Ein augmentiender Weg in
G
entspricht dann einem
gerichteten Pfad (d. h. einem Weg, der keine Knoten mehrfach
durchläuft) von
q
nach
s
in
G̃ . Ein solcher kann z. B. durch
Tiefen- oder Breitensuche gefunden werden.
graphen3.pdf, Seite 30
Gerichteter Graph im Beispiel
s , jeder in q beginnende
Pfad in G̃ führt zwagsläug über a, d und b nach q zurück.
Hier gibt es keinen Weg von
q
nach
Somit gibt keine weiteren augmentierenden Wege im Netzwerk
und der gefundene Fluss ist maximal.
graphen3.pdf, Seite 31
Bemerkungen
I Man kann Beispiele konstruieren, bei denen der
Algorithmus von FordFulkerson nicht nach endlich vielen
Schritten einen maximalen Fluss erreicht.
g (i , j ) ganzzahlig, so hat der
Algorithmus die Komplexität O (m · w ), wobei m die Zahl
der Kanten und w der Wert des maximalen Flusses ist.
Eine Variante ist der Algorithmus von Edmonds und Karp,
I Sind die Kapazitäten
I
bei dem immer der kürzeste augmentierende Weg gesucht
wird. Dieser Algorithmus hat in jedem Fall eine
polynomiale Komplexität.
I Der maximale Wert eines Flusses ist gleich der minimalen
Kapazität eines Schnittes
(Dualitätssatz von FordFulkerson).
graphen3.pdf, Seite 32
Im Beispiel: Kapazität eines Schnitts
Über die rote Linie können maximal 8 Einheiten transportiert
werden, d. h. der Schnitt hat Kapazität 8.
graphen3.pdf, Seite 33
Schnitt mit minimaler Kapazität 6
Ein Schnitt durch die Kanten
ac , bc
und
ds
hat die
Kapazität 6, die dem Wert des aktuellen Flusses entspricht.
Folglich ist der gefundene Fluss mit Wert 6 maximal. Alle
Kanten, die diesen Schnitt kreuzen, sind voll ausgelastet.
graphen3.pdf, Seite 34
Allgemeinere Netzwerke
s
s
I Hat ein Netzwerk mehrere Senken 1 , .., n , so fügt man
∗
∗
einen Noten Knoten
sowie Kanten von i nach
für
alle
i
s
s
s
mit jeweiliger Kapazität unendlich hinzu.
Ein maximaler Fluss im erweiterten Netzwerk mit Quelle
∗
und der einzigen Senke
entspricht dann einem
q
s
maximalen Fluss im ursprünglichen Netzwerk mit
mehreren Senken.
I Analog geht man bei einem Netzwerk mit mehreren
Quellen
q1 , ..., q
n
und Kanten von
vor: Man denietrt eine neue Quelle
∗
nach i für alle .
q
q
i
q∗
graphen3.pdf, Seite 35
Netzwerk mit mehreren Quellen und Senken
graphen3.pdf, Seite 36
Bemerkung
Je nach Anwendung können die neuen Kanten endliche
Kapazitäten zugewiesen bekommen.
Die Kapazität der Kante
q∗q
j
kann die maximale Menge
beschreiben, die von der Quelle
q
j
in das Netz eingespeist
werden kann.
Die Kapazität der Kante
s s∗
i
kann die maximale bzw.
gewünschte Menge angeben, die an der Senke
s
i
zu entnehmen
ist.
graphen3.pdf, Seite 37
Modellierung von Knoten mit beschränkter Kapazität
Hat ein (innerer) Knoten
i
nur eine beschränkte Kapazität
i
i
k,
so ersetzt man ihn durch zwei Knoten − und + , die durch
k verbunden sind.
Die bisher in i ankommenden Kanten (j , i ) kommen nun in i−
an, die von i ausgehenden Kanten gehen nun von i+ aus,
d. h. Kanten (j , i ) werden zu (j , i− ) und Kanten (i , j ) zu (i+ , j ).
Dies hat zur Folge, dass der gesamte durch i laufende Fluss
nun durch die neue Kante (i− , i+ ) laufen muss.
eine (neue) Kante
(i − , i + )
mit Kapazität
graphen3.pdf, Seite 38
Knoten i mit beschränkter Kapazität k
graphen3.pdf, Seite 39
Beispiel
Gegeben sei obiges Wasserleitungssystem mit zusätzlichen
Beschränkungen:
I
An der Quelle Q1 können maximal 5 Einheiten in das Netz
eingespeist werden, an Q2 6 Einheiten.
I
Am zentralen Knotenpunkt Z können maximal 9 Einheiten
durchgeleitet werden.
I
Die Verbraucher S1 und S3 möchten jeweils 3 Einheiten entnehmen,
S2 5 Einheiten.
graphen3.pdf, Seite 40
Erweiterter Graph
mit einer Quelle
Q∗
und einer Senke
S ∗.
graphen3.pdf, Seite 41
Maximaler Fluss
(nicht eindeutug bestimmt) mit Wert 11 und zwei Schnitte
minimaler Kapazität.
Da die Kanten
Q ∗ Q1
und
Q ∗ Q2
voll ausgelastet sind, wird die
maximal mögliche Menge in das Netzwerk eingespeist.
Da die Kanten
S1 S ∗ , S2 S ∗
und
S3 S ∗
voll ausgelastet sind,
können alle Verbraucher die gewünschte Menge entnehmen.
graphen3.pdf, Seite 42
Flüsse und Paarungen
G = (V , E ) mit V = L ∪ R
ein zugehöriges Netzwerk Ĝ = (V̂ , Ê ) deniert werden:
Zu jedem bipartiten Graphen
I
I
I
kann
V̂ = V ∪ {q , s } (zu den ursprünglichen Knoten wird eine
Quelle q und eine Senke s hinzugefügt.)
Die Kanten aus G bekommen in Ĝ die Richtung von L
nach R und die Kapazität 1.
Zusätzlich enthält Ê zu jedem Knoten l ∈ L eine Kante
(q , l ) mit Kapazität 1 und zu jedem Knoten r ∈ R eine
Kante (r , s ) mit Kapazität 1.
Dann entspricht jedem Matching in
zulässiger Fluss in
Ĝ
G
und umgekehrt.
Die zum Matching gehörenden Kanten
(q , l )
bzw.
dabei in
Ĝ
(r , s )
ein ganzzahliger
(l , r )
für alle gepaarten Knoten
l
sowie die Kanten
und
r
haben
Fluss 1, die übrigen Kanten Fluss 0.
graphen3.pdf, Seite 43
Matching und zugehöriger Fluss
Im Netzwerk haben alle Kanten die Richtung von links nach
rechts. Die grünen Kanten haben Fluss 1, die schwarzen
Kanten Fluss 0. Der Gesamtuss ist 2 und entspricht der Zahl
der Kanten im Matching.
graphen3.pdf, Seite 44
Augmentierende Wege
Jedem augmentierenden Weg bezüglich eines Matchings
entspricht ein augmentierender Weg bezüglich des zugehörigen
Flusses im Netzwerk.
Damit ist das Problem, ein maximales Matching zu nden, ein
Speziallfall des Problems, einen maximalen Fluss zu nden.
graphen3.pdf, Seite 45