A1 - Institut für Technische und Numerische Mechanik

Technische Mechanik II
SS17
A1.1
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 1: Arbeitsblatt zum Mohrschen Spannungskreis
Der ebene Spannungszustand im Punkt P eines Kontinuums führt bezüglich eines kartesischen Koordinatensystems auf die in der Skizze angegebenen Spannungen.
Gesucht sind die Hauptspannungen nach Größe und Richtung.
Der Lösungsweg wird am folgenden Zahlenbeispiel erläutert.
σ x = 140 N mm 2 ,
σ y = − 100 N mm 2 ,
τ xy = τ yx = − 90 N mm 2
Technische Mechanik II
SS17
A1.2
na
nb
nb
na
na
nb
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A1.3
Aufgabe 2: Teil einer Prüfungsaufgabe (Wintersemester 05/06)
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A1.4
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 3: Prüfungsaufgabe (Wintersemester 01/02)
Technische Mechanik II
SS17
A1.5
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A1.6
Schubspannung für einen um 45° entge-
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Ein Werkstattkran besteht aus einem waagerechten, einseitig eingespannten
I −Träger (Elastizitätsmodul E , Flächenträgheitsmoment I , Länge 2 a ) und
Technische Mechanik II
SS 17
A2.1
Skizze:
einer Laufkatze.
Der Träger ist in seiner Mitte
noch durch ein vertikales
Stahlseil (Elastizitätsmodul
E s , Querschnittsfläche A s )
gegen die Decke abgehängt. Im unverformten
Zustand der Konstruktion
hat das Seil die Länge L .
Die Eigengewichte von Träger und Seil seien vernachlässigbar.
Die Gewichte von Laufkatze
und Last können in einer
Einzelkraft F im variablen
Abstand r von der Einspannstelle A zusammengefasst werden.
A
b) Berechnen Sie die Lagerreaktionen F A , M A .
(Lassen Sie S als vorläufig unbekannt stehen)
FA =
_ _ _ _ _ _ _ _ _ _
MA =
_ _ _ _ _ _ _ _ _ _
c) Bestimmen Sie die Querkraft Q ( x ) , das Biegemoment M ( x ) , die
erste Ableitung der Biegelinie w ′ ( x ) und die Biegelinie w ( x ) mit Hilfe
von Klammerfunktionen. Setzen Sie die Ergebnisse von b) ein.
a) Tragen Sie am Balken die eingeprägten Kräfte und die Lagerreaktionen
F A , M A ein ( F A senkrecht zur x −Achse), und ersetzen Sie das Seil
durch die äquivalente Schnittkraft S . Ergänzen Sie die Skizze um die
geometrischen Abmessungen.
Q (x) =
________________________________
M (x) =
________________________________
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
E I w ′ (x) =
________________________________
E I w (x) =
________________________________
Technische Mechanik II
SS 17
A2.2
h) Die Seilkraft nimmt mit wachsender Entfernung der Laufkatze von der
Einspannstelle beständig zu.
Wie groß ist die maximale Seilkraft?
S max =
d) Wie groß ist der Biegepfeil f in der Balkenmitte?
EIf =
__________________________________
e) Wie groß ist die Dehnung ε des Seils?
ε =
f)
____________________________________
Geben Sie den Zusammenhang zwischen der Längenänderung ε und
der Spannung σ s im Seil an (Hookesches Gesetz).
σs =
____________________________________
g) Berechnen Sie die Seilkraft S .
S =
___________________________________
i)
_________________________________
Skizzieren Sie den Querkraft− Q ( x ) und Momentenverlauf M ( x ) für
die Werte r =
a
2
und S = F .
2
3
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 1: Prüfungsaufgabe Wintersemester 05/06
Technische Mechanik II
SS17
A3.1
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A3.2
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A3.3
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 2: Prüfungsaufgabe Sommersemester 2003
Technische Mechanik II
SS17
A3.4
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 3: Prüfungsaufgabe Wintersemester 2001/2002
Technische Mechanik II
SS17
A3.5
Technische Mechanik II
SS17
A4.1
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 1: Der Massenmittelpunkt eines starren Körpers habe in einem Inertialsystem den
Ortsvektor
r = [bsin(kt), bcos(kt),
𝑇
1
ct 2 ] , b, c, k = konst.
2
a) Wie lauten der Geschwindigkeits− und der Beschleunigungsvektor?
_____________________
𝐯=
_____________________
,
𝐚=
_____________________
_____________________
[_____________________]
[_____________________]
b) Ist der Betrag der Geschwindigkeit bzw. der Beschleunigung konstant?
ja
nein
v = konst.
a = konst.
Aufgabe 2:
Ein Massenpunkt m bewegt sich auf einer
ebenen, gekrümmten Bahn.
Welche der Skizzen sind kinematisch möglich?
a
v
a
v
a
v
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A4.2
Aufgabe 3: Gegeben ist das Geschwindigkeits−Zeit−Diagramm v = v(t) einer geradlinigen Bewegung in Richtung der x−Achse. Zeichnen sie den Weg x = x(t) mit der Anfangsbedingung des
Weges x(0) = 0 und die Beschleunigung a = a(t) maßstabsrichtig in die vorbereiteten Achsenkreuze ein.
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A4.3
Aufgabe 4: Ein Punkt P bewegt sich entlang der x−Achse. Die Lage des Punktes ist durch
1
𝑥 (𝑡) = 2 − 2𝑡 + 2𝑡 2 ,
0 ≤ 𝑡 ≤ 1,
gegeben.
a) Bestimmen Sie die Funktion 𝑥̇ = 𝑥̇ (𝑥) (Phasenkurve).
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
b) Zeichnen Sie die Phasenkurve in das gegebene Diagramm ein.
c) Markieren Sie die Punkte t = 0, t = 0.5 und t = 1 auf der Phasenkurve.
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A4.4
Aufgabe 5: Um die zulässige Höchstgeschwindigkeit von 50 km/h einzuhalten, leitet ein Autofahrer rechtzeitig vor einer geschlossenen Ortschaft den Bremsvorgang ein.
In welcher Entfernung vor dem Ortsschild muss er mit dem Bremsvorgang beginnen, wenn seine
Geschwindigkeit 100 km/h beträgt und die Bremsverzögerung während der Bremsdauer T linear
von 0 auf 0.7g (g = 9.81 m/s2 ) ansteigt?
a) Skizzieren Sie den Verlauf der Beschleunigung und der Geschwindigkeit des Bremsvorgangs.
b) Bestimmen Sie zunächst die Dauer T der Verzögerung.
T=_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
c) In welcher Entfernung s vor dem Ortsschild beginnt der Bremsvorgang?
s= _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 6: Eine von einem Motor angetriebene
Scheibe dreht sich um ihre Achse. Auf einem Messschrieb wurde die Winkelgeschwindigkeit 𝛼̇
der
Scheibe festgehalten.
Ermitteln Sie daraus den Verlauf des Drehwinkels 𝛼
und der Winkelbeschleunigung 𝛼̈ und zeichnen Sie
diese maßstabsrichtig in die Diagramme ein.
Für die Anfangsbedingungen gilt: 𝛼(𝑡 = 0) = 0.
Technische Mechanik II
SS17
A4.5
Technische Mechanik II
SS17
A5.1
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 1: Relativbewegung
Viele Punktbewegungen, die z.B. durch den Ortsvektor r = r(t) eines Punktes P in einem raumfesten Koordinatensystem K{O, x, y, z} gegeben sind, lassen sich einfacher beschreiben, wenn man
die Bewegung in einem geeignet gewählten bewegten Koordinatensystem K′{O′, x′, y′, z′} darstellt. Die Bewegung setzt sich dann zusammen aus der Relativbewegung in K′ und der Bewegung von K′.
Nun sei die Bewegung in K′ durch
r O′P K ′ = [ u(t), v(t), 0 ] T
und der Ortsvektor des Ursprungs O′ von K′ (beschrieben in K) durch
r OO′ K = [ 1, 1, 1 ] T
gegeben. Die Drehung von K′ gegen K werde durch folgende Transformationsmatrix dargestellt:
CKK ′
 0.6 0.8 cos ϕ − 0.8 sin ϕ 
=  − 0.8 0.6 cos ϕ − 0.6 sin ϕ  , ϕ = ϕ ( t ) .
 0
sin ϕ
cos ϕ 
Gesucht ist jetzt die Absolutgeschwindigkeit des Punktes P (gegenüber K), dargestellt in K′
v OP K′ = v OO′ K′ + ω KK′ K′ × rO′P K′ + v O′P K′ .
 ⋅C gewonnen werDer Drehvektor ω KK′ K (im K−System) kann aus dem Matrizenprodukt C
KK ′
K ′K
den:
 ′ ⋅C ′
C
KK
KK



=













=













⋅










Technische Mechanik II
SS17
A5.2
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Mit Hilfe des Rösselsprungs kann man ω KK ′ K ablesen
ω KK′ K

=

,



,
T
Welche Koordinaten hat ωKK ′ K′ ?
ω KK ′ K ′ = _ _ _ _ ω KK ′ K



=



 
 
 
⋅
 
 
 



=

















Welche Relativgeschwindigkeit hat der Punkt P (dargestellt in K′ )?
v O′P K′

d′
= rO′P K ′ = 
dt

,



,
T
Welche Absolutgeschwindigkeit hat der Punkt P (dargestellt in K′ )?
v OP K ′



= 



 
 
 
 + 
 
 
 
 
 
 
 + 
 
 
 
ω KK ′ K ′ × rO′P K ′
v OO′ K ′
 
 
 
 = 
 
 
 







v O′P K ′
Zum Vergleich soll jetzt die Absolutgeschwindigkeit im raumfesten Koordinatensystem K ermittelt
werden.
Welche Koordinaten hat dort der Ortsvektor r(t) des Punktes P?
r OP K



= 



 
 
 
⋅
 
 
 
CKK ′
 
 
 
 + 
 
 
 
rO′P K ′
 
 
 
 = 
 
 
 
r OO′ K







Technische Mechanik II
SS17
A5.3
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Die Absolutgeschwindigkeit in K erhält man durch Differenzieren der Koordinaten von rOP K (t)
nach der Zeit
v OP K =
d
rOP K
dt










= 



Zur Überprüfung der Rechnung wird v OP K ′ in das raumfeste System K transformiert.
v OP K



= 



 
 
 
⋅
 
 
 
CKK ′
Vergleichen Sie die beiden letzten Ergebnisse.
 
 
 
 = 
 
 
 
v OP K ′







Technische Mechanik II
SS17
A5.4
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 2:
Die Transformationsmatrix zwischen den Koordinatensystemen K und K′ lautet
CKK ′
0
0 
1

=  0 cos α − sin α  .
 0 sin α cos α 
a) Welche Lage haben die Systeme zueinander?
b) Wie lautet der Drehgeschwindigkeitsvektor ω KK ′ K , mit dem sich K′ gegen K dreht, dargestellt im System K?
ω KK ′ K

=

,
,



T
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Technische Mechanik II
SS17
A5.5
Aufgabe 3: Gegeben ist die Matrix der Richtungskosinusse für die beiden kartesischen Koordinatensysteme K und K′
CKK ′
 0 − sin ϕ cos ϕ 
=  1
0
0  ,
 0 cos ϕ sin ϕ 
ϕ = ω t, ω > 0 .
a) Welche Lage haben die Systeme zueinander?
b) Der Drehvektor ω KK ′ , mit dem sich K′ gegen K dreht, liegt in
positiver
x − Richtung
negativer
y − Richtung
z − Richtung.
Technische Mechanik II
SS17
A6.1
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
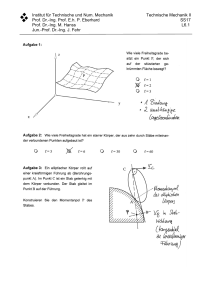
Aufgabe 1:
Wie viele Freiheitsgrade besitzt ein Punkt P, der sich
auf der skizzierten gekrümmten Fläche bewegt?
f=1
f=2
f=3
Aufgabe 2: Wie viele Freiheitsgrade hat ein starrer Körper, der aus zehn durch Stäbe miteinander verbundenen Punkten aufgebaut ist?
f=3
f=6
Aufgabe 3: Ein elliptischer Körper rollt auf
einer kreisförmigen Führung ab (Berührungspunkt A). Im Punkt C ist ein Stab gelenkig mit
dem Körper verbunden. Der Stab gleitet im
Punkt B auf der Führung.
Konstruieren Sie den Momentanpol P des
Stabes.
f = 30
f = 60
Technische Mechanik II
SS17
A6.2
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 4:
Die Stäbe AB und CD sind bei C durch ein
Gelenk verbunden und gleiten in einer
rechteckigen Vertiefung mit glatten Seitenwänden.
Wo liegen die Momentanpole PAB und PCD
der Stäbe AB und CD in der skizzierten Lage?
Pol
Punkt
A
B
C
D
E
F
PAB
PCD
Aufgabe 5:
Konstruieren Sie die Geschwindigkeit des Punktes C nach Größe und Richtung.
G
H
Technische Mechanik II
SS17
A6.3
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 6:
Eine exzentrisch gelagerte Kreisscheibe
drehe sich in der x,y−Ebene mit der Winkel-
 um die z−Achse. Die
geschwindigkeit ω = ψ
Lage des Punktes Q der Scheibe sei durch
den Winkel ϕ zwischen OM und MQ festgelegt.
a) Welche Koordinaten hat der Ortsvektor r
von Q im Koordinatensystem {x, y, z}?


 ______________ 




r = 

 ______________ 




 _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
b) Welche Koordinaten hat die Geschwindigkeit v von Q?
v =

 ______________________



 ______________________


 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _









c) Welcher Punkt ist der Momentanpol P der Scheibe?
P=M
P=O
P=Q
Technische Mechanik II
SS17
A6.4
Institut für Technische und Num. Mechanik
Prof. Dr.-Ing. Prof. E.h. P. Eberhard
Prof. Dr.-Ing. M. Hanss
Jun.-Prof. Dr.-Ing. J. Fehr
Aufgabe 7:
Ein Punkt P bewege sich geradlinig auf der
x−Achse. Zur Zeit t 0 = 0 sei er an der Stelle
x = x0 > 0 .
Seine Geschwindigkeit v =
dx
dt
sei stets
zum Ursprung O gerichtet, ihr Betrag sei
proportional
zum
Abstand
x vom Ur-
sprung O (Proportionalitätsfaktor k > 0 ).
a) Wie lauten die Funktionen v = v ( x ) , a = a ( x ) und x = x ( t ) ?
Dabei sei a =
d2x
die Beschleunigung von P.
dt 2
v( x ) = _ _ _ _ _ _ _ _ _ _ _ _ _ ,
a (x) = _ _ _ _ _ _ _ _ _ _ _ _ ,
x(t) = _ _ _ _ _ _ _ _ _ _ _ _
b) Erreicht P den Ursprung in endlicher Zeit?
Ja
Aufgabe 8: Der Bewegungswinder eines starren
Körpers im Punkt B sei ( ω , v B ).
Wie lautet der äquivalente Winder im Punkt A?


 _ _ _ _ _ _,



_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 
Nein