Statistische Formeln in Excel Beschreibung =MTTELWERT(A1:F1

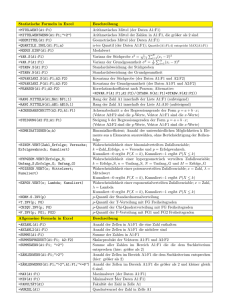
Statistische Formeln in Excel
=MTTELWERT(A1:F1)
=GEOMITTEL(A1:F1)
=HARMITTEL(A1:F1)
=MITTELWERTWENN(A1:F1;”>2”)
=VAR.S(A1:F1)
=VAR.P(A1:F1)
=STABW.S(A1:F1)
=STABW.N(A1:F1)
=QUARTILE.INKL(A1:F1;n)
=KOVARIANZ.S(A1:F1;A2:F2)
=KOVARIANZ.P(A1:F1;A2:F2)
=PEARSON(A1:F1;A2:F2)
=ACHSENABSCHNITT(A2:F2;A1:F1)
=STEIGUNG(A2:F2;A1:F1)
=RANG.MITTELW(A1;$A1:$F1;1)
=MODUS.EINF(A1:F1)
=SCHIEFE(A1:F1)
=BINOM.VERT(Zahl_Erfolge; Versuche;
Erfolgswahrsch; Kumuliert)
=HYPGEOM.VERT(Erfolge_S;
Umfang_S;Erfolge_G; Umfang_G)
=POISSON.VERT(x; Mittelwert;
Kumuliert)
=EXPON.VERT(x; Lambda; Kumuliert)
=NORM.S.INV(γ)
=T.INV(γ; FG)
=CHIQU.INV(γ; FG)
=F.INV(γ; FG1; FG2)
Allgemeine Formeln in Excel
=ANZAHL(A1:F1)
=ANZAHL2(A1:F1)
=SUMME(A1:F1)
=SUMMENPRODUKT(A1:F1; A2:F2)
=SUMMEWENN(A1:F1; ”>2”)
Beschreibung
Arithmetisches Mittel (der Daten A1:F1)
Geometrisches Mittel (der Daten A1:F1)
Harmonisches Mittel (der Daten A1:F1)
Arithmetisches Mittel der Zahlen in A1:F1, die größer als 2 sind
PN
Varianz der Stichprobe s2 = N 1−1 i=1 (xi − x)2
PN
Varianz der Grundgesamtheit σ 2 = N1 i=1 (xi − x)2
Standardabweichung der Stichproben
Standardabweichung der Grundgesamtheit
n-tes Quartil (der Daten A1:F1);
Quartile(A1:F1;4) entspricht MAX(A1:F1)
Kovarianz der Stichprobe (der Daten A1:F1 und A2:F2)
Kovarianz der Grundgesamtheit (der Daten A1:F1 und A2:F2)
Korrelationskoeffizient nach Pearson;
Alternative: =KOVAR(A1:F1;A2:F2)/(STABWN(A1:F1)*STABWN(A2:F2))
Achsenabschnitt a der Regressionsgerade der Form y = a + b · x;
(Vektor A2:F2 sind die y-Werte, Vektor A1:F1 sind die x-Werte)
Steigung b der Regressionsgeraden der Form y = a + b · x;
(Vektor A2:F2 sind die y-Werte, Vektor A1:F1 sind die x-Werte)
Rang der Zahl A1 innerhalb der Liste A1:F1 (aufsteigend)
Modalwert
Symmetrieparameter γ
Wahrscheinlichkeit einer binomialverteilten Zufallsvariable;
k =Zahl_Erfolge, n = Versuche und p = Erfolgswahrsch.
Kumuliert=0 ergibt P (X = k), Kumuliert=1 ergibt P (X ≤ k)
Wahrscheinlichkeit einer hypergeometrisch verteilten Zufallsvariable;
k = Erfolge_S, n = Umfang_S, N = Umfang_G und M = Erfolge_G
Wahrscheinlichkeit einer poissonverteilten Zufallsvariable; x = Zahl, λ =
Mittelwert
Kumuliert=0 ergibt P (X = k), Kumuliert=1 ergibt P (X ≤ k)
Wahrscheinlichkeit einer exponentialverteilten Zufallsvariable; x = Zahl,
λ = Lambda
Kumuliert=0 ergibt P (X = k), Kumuliert=1 ergibt P (X ≤ k)
γ-Quantil der Standardnormalverteilung
γ-Quantil der T-Verteilung mit FG Freiheitsgraden
γ-Quantil der Chi-Quadratverteilung mit FG Freiheitsgraden
γ-Quantil der F-Verteilung mit FG1 und FG2 Freiheitsgraden
Beschreibung
Anzahl der Zellen in A1:F1 die eine Zahl enthalten
Anzahl der Zellen in A1:F1 die nichtleer sind
Summe der Zahlen in A1:F1
Skalarprodukt der Vektoren A1:F1 und A2:F2
Summe aller Zahlen im Bereich A1:F1 die dem Suchkriterium
entsprechen (hier: größer als 2)
=ZÄHLENWENN(A1:F1;”>2”)
Anzahl der Zellen im Bereich A1:F1 die dem Suchkriterium entsprechen
(hier: größer als 2)
=ZÄHLENWENNS(A1:F1;”>2”;A1:F1;”<=6”) Anzahl der Zellen im Bereich A1:F1 die größer als 2 und kleiner gleich
6 sind.
=MAX(A1:F1)
Maximalwert (der Daten A1:F1)
=MIN(A1:F1)
Minimalwert (der Daten A1:F1)
=FAKULTÄT(A1)
Fakultät der Zahl in Zelle A1
1 der Zahl in Zelle A1
=WURZEL(A1)
Quadratwurzel