Institut für Mechanik Prof. Dr.-Ing. habil. P. Betsch Prof. Dr

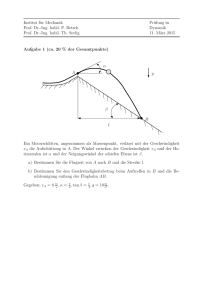
Institut für Mechanik
Prof. Dr.-Ing. habil. P. Betsch
Prof. Dr.-Ing. habil. Th. Seelig
Prüfung in
Dynamik
12. August 2015
Aufgabe 1 (ca. 18 % der Gesamtpunkte)
r
g
l
θ
m
In der Abbildung ist ein rotierendes Karussell skizziert. Sitz und Fahrgast können
als Massenpunkt m angesehen werden. Das Karussell rotiert mit konstanter Winkelgeschwindigkeit. Wie groß ist die Geschwindigkeit der Fahrgäste auf dem Karussell,
wenn die Halteseile (Länge l) um den Winkel θ gegen die Senkrechte geneigt sind?
Gegeben: θ, m, g, r, l.
Institut für Mechanik
Prof. Dr.-Ing. habil. P. Betsch
Prof. Dr.-Ing. habil. Th. Seelig
Prüfung in
Dynamik
12. August 2015
Aufgabe 2 (ca. 25 % der Gesamtpunkte)
Ein massiver Kreiszylinder rollt schlupffrei auf einer horizontalen Ebene und wird von
einer Feder mit der Federkonstanten c und einem Dämpfer mit der Dämpfungskonstanten d, die im Abstand a vom Mittelpunkt angreifen, in der dargestellten Mittellage
gehalten. Im abgebildeten Zustand ist die Feder entspannt.
g
ϕ
d
c
a
r
S
m
a) Schneiden Sie das System frei und stellen Sie mit Hilfe der synthetischen Methode
die Bewegungsgleichungen für kleine Auslenkungen aus der Gleichgewichtslage auf.
b) Berechnen Sie den Dämpfungsgrad D, die Eigenfrequenzen ω und ωd des Systems
bei kleinen Auslenkungen.
c) Wie groß muss die Dämpfungskonstante d gewählt werden, damit der aperiodische
Grenzfall eintritt.
Gegeben: r, a, m, c, d, g
Institut für Mechanik
Prof. Dr.-Ing. habil. P. Betsch
Prof. Dr.-Ing. habil. Th. Seelig
Prüfung in
Dynamik
12. August 2015
Aufgabe 3 (ca. 22 % der Gesamtpunkte)
A und B sind reibungsfrei gelagert und durch einen dünnen,
Zwei homogene Walzen masselosen Riemen schlupffrei miteinander verbunden. Nach dem Ausschalten des anA gleich ω0 . Um die
treibenden Motors ist die Winkelgeschwindigkeit der Walze A mit einer konstanten
Drehung abzubremsen, wird ein Bremsklotz an der Walze Kraft N angepresst. Der Gleitreibungskoeffizient zwischen der Walze und dem Klotz
sei µ.
A
B
ϕA
R
r
N
θA
µ
ϕB
θB
A von Beginn der Bremsung zum
Bestimmen Sie wie viele Umdrehungen n die Walze Zeitpunkt t0 bis zum vollständigen Anhalten vollzieht.
Geg.: N, µ, θA , θB , R, r, ϕ̇A (t0 ) = ω0 , ϕA (t0 ) = 0
Institut für Mechanik
Prof. Dr.-Ing. habil. P. Betsch
Prof. Dr.-Ing. habil. Th. Seelig
Prüfung in
Dynamik
12. August 2015
Aufgabe 4 (ca. 35 % der Gesamtpunkte)
k
m
m
k
ϕ
y
L
L
L
Ein starrer, masseloser Stab der Länge 3L ist an den Enden durch gleiche Federn der
Steifigkeit k gelagert. Im Abstand L von außen sind am Stab die Massenpunkte m
befestigt.
Durch entsprechende Maßnahmen findet keine Horizontalbewegung statt. Die Bewegung des Systems wird daher allein durch die y-Koordinate des Schwerpunktes und
den Winkel ϕ beschrieben. Der Einfluss des Schwerefeldes ist im folgenden nicht zu
berücksichtigen. Es kann von kleinen Auslenkungen aus der Ruhelage ausgegangen
werden.
a) Berechnen Sie die kinetische Energie Ek .
b) Berechnen Sie die potentielle Energie Ep der Federn.
c) Ermitteln Sie mit Hilfe des Lagrangeschen Formalismus die Bewegungsgleichungen.
d) Wie groß sind die Eigenkreisfrequenzen?
e) Skizzieren Sie die Eigenformen!
Gegeben: m, k, L
Lösung zu Aufgabe 1
z
r
θ
l
θ
S
m
m
R
G
r
y
v
eϕ er
m
R
ϕ
x
ω = ϕ̇
R = r + l sin(θ)
F = ma
ar = r̈ − r ϕ̇2
aϕ = r ϕ̈ + 2ṙϕ̇
  

  

Fr
−S sin(θ)
ar
−Rϕ̇2

0
F = Fϕ  = 
a = aϕ  =  0 
Fz
S cos(θ) − G
az
0
Komponentenweise:
−S sin(θ) = −mRω 2
S cos(θ) − G = 0
(1)
(2)
Aus (2):
S=
mg
cos(θ)
(3) in (1):
6 mg
sin(θ) = − 6 m(r + l sin(θ))ω 2
cos(θ)
g
ω 2 = tan(θ)
r + l sin(θ)
r
g
ω = tan(θ)
r + l sin(θ)
p
mit v = ωR = tan(θ)g(r + l sin(θ))
(3)
Lösung zu Aufgabe 2
a) Freikörperbild:
x
ϕ
Fd Fc
r+a
A
Momentanpol
Bewegungsgleichung (Drallsatz):
θA ϕ̈ = − Fd (r + a) − Fc (r + a)
(4)
Dämpfungskraft und Federkraft:
Kinematik:
Fd = d ẋ
Fc = c x
(5)
x = (r + a) ϕ
ẋ = (r + a) ϕ̇
(6)
eingesetzt in die Bewegungsgleichung:
θA ϕ̈ + d ( r + a )2 ϕ̇ + c ( r + a )2 ϕ = 0
(7)
mit
θA = θS + m r 2 =
folgt:
ϕ̈ +
3
2
1
2
m r2 + m r2 =
d
( r + a )2 ϕ̇ +
2
mr
3
2
3
2
m r2
c
( r + a )2 ϕ = 0
2
mr
(8)
b) die Eigenfrequenz des ungedämpften Systems:
ω02 =
ω0 =
3
2
c
( r + a )2
m r2
r
2c
3m
r +a
r
(9)
(10)
der Dämpfungsgrad:
2 D ω0 =
3
2
d
( r + a )2
m r2
d
( r + a )2
3 ω0 m r 2
die Eigenfrequenz des gedämpften Systems:
q
√
r +a
2
2
2
2
6 m r c − d ( r + a)
ωd = ω0 1 − D =
3 m r2
D =
c) Der aperiodischer Grenzfall tritt ein wenn D = 1. Die Gleichung (12) folgt:
r
√
r
3 m r2
2c r + a
3 ω0 m r 2
=
=
d =
6mc
( r + a )2
( r + a )2 3 m
r
r+a
(11)
(12)
(13)
(14)
Lösung zu Aufgabe 3
Kinematik
R
r
R
⇒ ϕ˙B = ϕ˙A ·
r
ϕA · R = ϕB · r ⇔ ϕB = ϕA ·
0 →
1
Arbeitssatz (Ek )0 + W01 = (Ek )1
1
1
⇔ θA ϕ̇2A,0 + θB ϕ̇2B,0 + W01 = 0
2
2
Dissipierte Bremsenenergie
W01 =
Zx1
F dx
x0
mit F = −FR = −µN
dx = R · dϕ
Z ϕA,1
⇒ W01 = −
µNRdϕ
ϕA,0
= −µNRϕ1
Eingesetzt in Arbeitssatz
1
1
θA ϕ̇2A,0 + θB ϕ̇2B,0 − µNRϕ1 = 0
2
2
1
R2
1
⇔ θA ω02 + θB ω02 2 − µNRϕ1 = 0 (Kinematik eingesetzt)
2
2
r
1
R2
1
· (θA + 2 θB )ω02
⇔ ϕ1 =
µNR 2
r
mit ϕ1 = 2πn
1
R2
⇒n=
· (θA + 2 θB )ω02
2µNR · 2π
r
Lösung zu Aufgabe 4
a) Kinetische Energie:
1
1
EK = (2m)ẏ 2 + θS ϕ̇2
2
2
L 2 m 2
θS = 2m( ) = L
2
2
b) Potentielle Energie:
3
1
3
1
EP = k(y + Lϕ)2 + k(y − Lϕ)2
2
2
2
2
c)
1
1
3
1
3
L = EK − EP = mẏ 2 + θS ϕ̇2 − k(y + Lϕ)2 − k(y − Lϕ)2
2
2
2
2
2
d ∂L
( ) = 2mÿ
dt ∂ ẏ
∂L
3
3
= −k(y + Lϕ) − k(y − Lϕ)
∂y
2
2
d ∂L
( ) = θS ϕ̈
dt ∂ ϕ̇
∂L
3
3
3
3
= −k(y + Lϕ) L − k(y − Lϕ)(− L)
∂ϕ
2
2
2
2
Bewegungsgleichungen:
3
3
2mÿ + k(y + Lϕ) + k(y − Lϕ) = 0
2
2
3
3
3
3
θS ϕ̈ + k(y + Lϕ)( L) − k(y − Lϕ)( L) = 0
2
2
2
2
Umformen:
6 2mÿ+ 6 2ky = 0
k
ÿ + y = 0
m
9 2
θS ϕ̈ + L kϕ = 0
2
9L2 k
ϕ=0
ϕ̈ +
2θS
d) Die Bewegungsgleichungen sind entkoppelt. Die Eigenkreisfrequenzen sind einfach:
r
r
r
r
k
k
k
k
ω2 = 3L
= 3L
=3
ω1 =
2
m
2θS
mL
m
e)
1EF
ϕ≡0
k
ω12 =
m
2EF
y≡0
k
ω22 = 9
m