2001-2002-3-LK Binaerbaum ALI\374

3. INFORMATIK-KLAUSUR
Name:
04.03.2002
− Seite 1 −
Bearbeitungszeit: 135 min
Info 12 LK (GA)
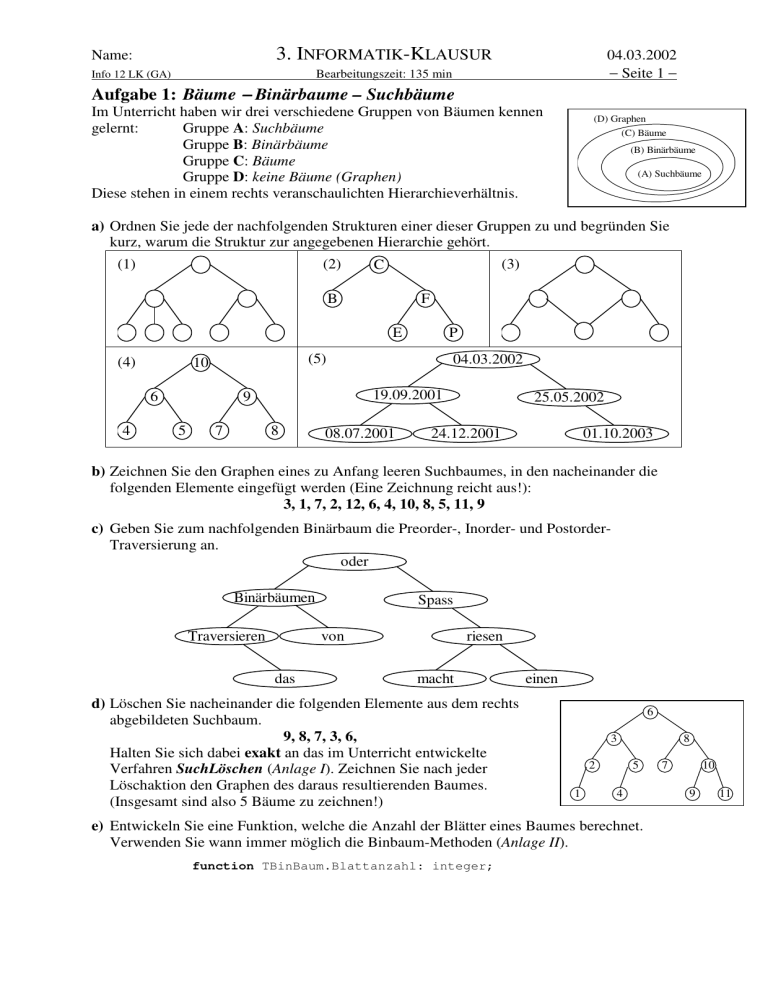
Aufgabe 1: Bäume − Binärbaume – Suchbäume
Im Unterricht haben wir drei verschiedene Gruppen von Bäumen kennen
gelernt:
Gruppe A: Suchbäume
Gruppe B: Binärbäume
Gruppe C: Bäume
Gruppe D: keine Bäume (Graphen)
Diese stehen in einem rechts veranschaulichten Hierarchieverhältnis.
(D) Graphen
(C) Bäume
(B) Binärbäume
(A) Suchbäume
a) Ordnen Sie jede der nachfolgenden Strukturen einer dieser Gruppen zu und begründen Sie
kurz, warum die Struktur zur angegebenen Hierarchie gehört.
(2)
(1)
(3)
C
B
F
E
(4)
(5)
10
6
4
7
04.03.2002
19.09.2001
9
5
P
8
08.07.2001
25.05.2002
24.12.2001
01.10.2003
b) Zeichnen Sie den Graphen eines zu Anfang leeren Suchbaumes, in den nacheinander die
folgenden Elemente eingefügt werden (Eine Zeichnung reicht aus!):
3, 1, 7, 2, 12, 6, 4, 10, 8, 5, 11, 9
c) Geben Sie zum nachfolgenden Binärbaum die Preorder-, Inorder- und PostorderTraversierung an.
oder
Binärbäumen
Traversieren
Spass
von
das
riesen
macht
d) Löschen Sie nacheinander die folgenden Elemente aus dem rechts
abgebildeten Suchbaum.
9, 8, 7, 3, 6,
Halten Sie sich dabei exakt an das im Unterricht entwickelte
Verfahren SuchLöschen (Anlage I). Zeichnen Sie nach jeder
Löschaktion den Graphen des daraus resultierenden Baumes.
(Insgesamt sind also 5 Bäume zu zeichnen!)
einen
6
3
2
1
8
5
4
e) Entwickeln Sie eine Funktion, welche die Anzahl der Blätter eines Baumes berechnet.
Verwenden Sie wann immer möglich die Binbaum-Methoden (Anlage II).
function TBinBaum.Blattanzahl: integer;
7
10
9
11
3. INFORMATIK-KLAUSUR
Name:
04.03.2002
− Seite 2 −
Bearbeitungszeit: 135 min
Info 12 LK (GA)
Aufgabe 2: ALI – von der Hochsprache zur Maschinenebene
a) Schreiben Sie ein Pascal- sowie das zugehörige RePascal-PROGRAM Quadratsumme,
welches nach Eingabe einer natürlichen Zahl n die Summe der ersten n natürlichen
Quadratzahlen, d.h. 12 + 22 + 32 + ... + n2, berechnet und anschließend ausgibt.
Übersetzen Sie das Programm anschließend aus der Zwischensprache nach ALI!
b) Die Summe aus Teilaufgabe a) soll nun mit Hilfe der Formel
n(n + 1)(2n + 1)
berechnet werden.
12 + 2 2 + 3 2 + ... + n 2 =
6
Notieren Sie die Umwandlung der Zuweisung Summe:= n*(n+1)*(2*n+1) div 6 in
das Dreiadressformat mit Hilfe des Zerlegungsalgorithmus aus Anlage III (Achtung:
Endergebnis alleine reicht nicht aus; dokumentieren Sie die Ausführung des Algorithmus
u. a. mit passenden Stacks und Zwischenergebnissen).
Gegeben ist folgendes Pascal-Programm:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
program WasTueIch;
var i, j: integer;
hilf: integer;
feld: array[-6..2] of integer;
begin
for i := -6 to 2 do readln(feld[i]);
for i := -6 to 2
do begin
j:= i;
while (j > -6) and (feld[j] < feld[j-1])
do begin
hilf
:= feld[j];
feld[j] := feld[j-1];
feld[j-1]:= hilf;
j := j - 1;
end;
end;
end;
c) Veranschaulichen Sie den obigen Algorithmus an der folgenden Feld-Belegung.
0
1
−6
−5
−4
−3
−2
−1
6
3
1
7
5
9
2
4
2
8
Geben Sie dazu jedes Mal, wenn sie die Zeile 15 passieren, die aktuelle Feldbelegung an.
Der Anfang wurde bereits gemacht.
−6
−5
−4
−3
−2
−1
0
1
2
6
3
3
1
3
6
1
3
1
1
6
6
7
7
7
7
5
5
5
5
9
9
9
9
2
2
2
2
4
4
4
4
8
8
8
8
Erläuteren Sie, was der Algorithmus leistet und geben Sie ihm anschließend den aus
Informatikersicht korrekten Namen.
d) Übersetzen Sie den Algorithmus in die Zwischensprache RePascal.
e) Übersetzen Sie die for-Schleife zur Dateneingabe (Zeilen 6) in ALI!
Viel Erfolg!
Anlage II:
{
{
{
{
{
{
{
{
{
{
{
{
{
{
{
Der Datentyp TBinbaum in Delphi
----------------------------------------------------------------------------------------------------------------- }
}
Die Unit stellt einen inhaltslosten Datentypen TBinBaum zur Verfügung. Um einen Binärbaum mit Inhalt zu erhalten, }
muss eine hiervon abgeleitete Klasse erstellt werden, z. B.:
}
}
type TIntBinBaum = class(TBinBaum)
}
public
}
Wurzelinhalt: integer;
}
constructor Create(w: Integer);
}
function WurzelinhaltToString: string; override;
}
end;
}
}
Ein Binärbaum kann entweder leer sein (NIL) oder eine Wurzel mit zwei evtl. leeren Teilbäumen rtb, ltb
}
}
----------------------------------------------------------------------- Tool zum Binärbaum, (C) 2001 D. Garmann - }
unit Binbaum;
interface
type
TBinBaum = class
private
ltb, rtb: TBinBaum;
public
constructor Create;
destructor
function
function
function
function
procedure
procedure
function
function
function
function
function
end;
{ Erzeugt ein Blatt, d.h. "leeres Element mit rtb=ltb=NIL
}
Destroy;
{ Zerstört das Element inklusive seiner Teilbäume
}
Leer: boolean;
{ Liefert "true" wenn der Baum leer ist, d. h. der Baum ist = NIL
}
WurzelinhaltToString: string; virtual; abstract;
{ Abstracte Methode zur Darstellung des Inhalts auf dem Bildschirm (Editfeld, etc.) }
LinkerTeilbaum: TBinBaum;
{ Liefert den Linken Teilbaum im Funktionsergebnis zurück.
RechterTeilbaum: TBinBaum;
{ Liefert den Rechten Teilbaum im Funktionsergebnis zurück.
FuegeTeilbaumLinksAn(tb: TBinBaum);
{ Fügt einen Teilbaum an das aktuelle
{ VORSICHT! Ein eventuell vorhandener
FuegeTeilbaumRechtsAn(tb: TBinBaum);
{ Fügt einen Teilbaum an das aktuelle
{ VORSICHT! Ein eventuell vorhandener
}
}
Baumelement links an.
linker Teilbaum geht verloren!
}
}
Baumelement rechts an.
rechter Teilbaum geht verloren!
}
}
LinksLeer: Boolean;
{ Liefert "true" wenn der linke Teilbaum leer ist, d. h. ltb=NIL
{ VORSICHT! Ein leerer Baum hat keinen linken Teilbaum => Laufzeitfehler
RechtsLeer: Boolean;
{ Liefert "true" wenn der rechte Teilbaum leer ist, d. h. rtb=NIL
{ VORSICHT! Ein leerer Baum hat keinen rechten Teilbaum => Laufzeitfehler
IstBlatt: Boolean;
{ Liefert "true", wenn das aktuelle Element leere Teilbäume hat.
ErsetztDurchLinkenTeilbaum: TBinBaum;
{ Liefert den Linken Teilbaum im Funktionsergebnis zurück und LÖSCHT den Rest.
ErsetztDurchRechtenTeilbaum: TBinBaum;
{ Liefert den Rechten Teilbaum im Funktionsergebnis zurück und LÖSCHT den Rest.
}
}
}
}
}
}
}
Anlage I:
Ja
Algorithmus Suchlöschen
aktueller Baum leer?
Ja
Nein
aktueller Baum „gleich“ Suchelement?
Nein
akt. Baum „größer“ Suchel.?
{Nicht gefunden}
•
{gefunden}
Führe „EchtLöschen“
aus
ExistiertBereits
↑
FALSCH
ExistiertBereits
↑
WAHR
•
Ja
Betrachte den
linken
Teilbaum und
führe
„Suchlöschen“
darin aus
Hänge diesen
Teilbaum wieder
an den aktuellen
Baum links an
Nein
• Betrachte den
rechten Teilbaum
und führe
„Suchlöschen“
darin aus
• Hänge diesen
Teilbaum wieder
an den aktuellen
Baum rechts an
Algorithmus: „EchtLöschen“
Ja
aktueller Baum rechts leer?
Nein
aktueller Baum links leer?
Ersetze akt. Baum
durch linken
Teilbaum
Ja
Ersetze akt. Baum
durch rechten
Teilbaum
{inklusive Blatt
abschneiden}
{inklusive Blatt
abschneiden}
•
•
•
•
•
Nein
Betrachte den linken Teilbaum
„IsolieregrößtesElement:“ darin:
GroesstesElement
Hänge beide Teilbäume vom aktuellen
Baum an das GroesstesElement
Isoliere die Wurzel des aktuellen Baumes
und gib dafür den Speicher frei
Ändere den aktuellen Baum ab in
GroesstesElement
Anlage III:
Der Zerlegungsalgorithmus
Zerlegung
Zerlegung:
TZeichenketten (z. B. als Schlange oder Liste)
Ausdruck:
TZeichenkette
ODK, OTK:
TKeller (= TStack)
Zeichen:
TZeichen
• Richte zwei Keller ein (ODK, OTK)
• Wiederhole
• Lies das nächste Zeichen.
• Falls das Zeichen
a) ein Operand ist,
• kellere ihn im ODK ein (push)
b) ein Operator ist,
• überprüfe seine Priorität.
• Solange der Operator keine Priorität gegenüber dem obersten Operator
• des OTK besitzt,
wiederhole: • werte den OTK aus.
• Speichere den neuen Operator im OTK.
c) eine öffnende Klammer ist,
• speichere diese im OTK.
d) eine schließende Klammer ist,
• führe eine Auswertung aller Operatoren zurück bis zur
• entsprechenden öffnenden Klammer aus
• entferne die öffnende Klammer aus dem OTK (pop).
• bis Ausdruck ganz abgearbeitet ist.
• Solange der OTK nicht leer ist,
wiederhole: • werte den OTK aus.
ALGORITHMUS
I/O-OBJEKTE
Inp-OBJEKT
HILFSOBJ.
3. INFORMATIK-KLAUSUR
04.03.2002
− Seite 1 −
Lösungen
Info 12 LK (GA)
Aufgabe 1: Bäume − Binärbaume – Suchbäume
a) (1): Gruppe C. Nicht B, da 3 Teilbäume an einem Knoten hängen
(2): Gruppe A.
(3): Gruppe D. Nicht C, da ein Knoten zwei Väter hat.
(4): Gruppe B. Nicht A, da Ordnungsrelation verletzt.
(5): Gruppe A.
b) Der Baum sieht wie folgt aus:
c) PreOrder: oder Binärbäumen Traversieren das von Spass riesen macht einen
InOrder: Traversieren das Binärbäumen von oder Spass macht reisen einen
PostOrder: das Traversieren von Binärbäumen macht einen riesen Spass oder
d) Die Bäume sehen wie folgt aus:
6
3
2
8
5
1
6
7
3
10
4
2
11
6
3
2
1
4
5
1
10
4
11
6
10
5
7
2
11
1
5
10
5
2
11
1
10
4
4
e) Eine Implementierung könnte wie folgt aussehen:
function TBinBaum.Blattanzahl: integer;
begin
if leer
then Blattanzahl:= 0
else if istBlatt
then Blattanzahl:= 1
else Blattanzahl:= linkerTeilbaum.Blattanzahl +
rechterTeilbaum.Blattanzahl;
end;
11
3. INFORMATIK-KLAUSUR
04.03.2002
− Seite 2 −
Lösungen
Info 12 LK (GA)
Aufgabe 2: ALI – von der Hochsprache zur Maschinenebene
a) Der Algorithmus sieht wie folgt aus:
program Quadsum;
var n: integer;
i, Summe: integer;
begin
Summe:= 0;
Readln(n);
for i:= 1 to n
do Summe:= Summe + i * i;
Writeln(Summe);
end.
Quadsum START
L
ST
INI
L
ST
M1
L
C
BH
L
M
ST
L
A
ST
L
A
ST
B
M2
OUTI
EOJ
n
DS
i
DS
Summe
DS
h1
DS
END
program Quadsum_RePascal;
var n: integer;
i, Summe: integer;
h1: integer;
label M1, M2;
begin
Summe:= 0;
Readln(n);
i:= 1;
M1: if i > n then goto M2;
h1:= i * i;
Summe:= Summe + h1;
i:= i + 1;
goto M1;
M2: Writeln(Summe);
end.
0
0,’0’
0,Summe
n
0,’1’
0,i
0,i
0,n
M2
0,i
0,i
0,h1
0,Summe
0,h1
0,Summe
0,i
0,’1’
0,i
M1
Summe
F
F
F
F
Quadsum
b) Die Formel Summe:= n*(n+1)*(2*n+1) div 6 wir im Dreiadressformat zu:
div
+
*
(
*
+
(
*
:=
h6
6
h5
h4
1
h3
n
2
h2
h1
1
n
n
Summe
OTK
ODK
h1:= n + 1;
h2:= n * h1;
h3:= 2 * n;
h4:= h3 + 1;
h5:= h2 * h4;
h6:= h5 div 6;
Summe:= h6;
c) Der Algorithmus könnte wie folgt veranschaulicht werden:
−6
−5
−4
−3
−2
−1
0
1
2
6
3
1
7
5
9
2
4
8
3
6
1
7
5
9
2
4
8
3
1
1
3
6
6
7
7
5
5
9
9
2
2
4
4
8
8
1
3
6
7
5
9
2
4
8
1
1
3
3
6
5
5
6
7
7
9
9
2
2
4
4
8
8
1
3
5
6
7
9
2
4
8
1
1
1
1
1
3
3
3
3
2
5
5
5
2
3
6
6
2
5
5
7
2
6
6
6
2
7
7
7
7
9
9
9
9
9
4
4
4
4
4
8
8
8
8
8
1
1
1
1
2
2
2
2
3
3
3
3
5
5
5
4
6
6
4
5
7
4
6
6
4
7
7
7
9
9
9
9
8
8
8
8
1
2
3
4
5
6
7
8
9
Der Algorithmus sortiert die eingegebenen Zahlen mit Hilfe des Verfahrens InsertionSort.
3. INFORMATIK-KLAUSUR
04.03.2002
− Seite 3 −
Lösungen
Info 12 LK (GA)
d) Die Übersetzung sieht wie folgt aus:
program WasTueIch;
var i, j: integer;
hilf: integer;
feld: array[-6..2] of integer;
h1: integer;
label M1, M2, M3, M4, M5, M6;
begin
i:= -6;
M1: if i > 2 then goto M2;
readln(feld[i]);
i:= i + 1;
goto M1;
M2: i:= -6;
M3: if i > 2 then goto M4;
j:= i;
M5: if j <= -6 then goto M6;
h1:= j - 1;
if j feld[j] >= feld[h1] then goto M6;
hilf
:= feld[j];
feld[j] := feld[h1];
feld[h1]:= hilf;
j:= j - 1;
goto M5;
M6: i:= i + 1;
goto M3;
M4:
end.
e) Die ALI-Übersetzung der While-Schleife ist wie folgt (hier das ganze Programm):
InsSort
M1
M2
M3
M5
START
L
ST
L
C
BH
L
S
M
INI
L
A
ST
B
L
ST
L
C
BH
L
ST
L
C
BNH
L
S
ST
L
S
M
L
L
S
M
C
0
0,'-6'
0,i
0,i
0,'2'
M2
4,i
4,'-6'
4,'2'
feld(4)
0,i
0,'1'
0,i
M1
0,'-6'
0,i
0,i
0,'2'
M4
0,i
0,j
0,j
0,'-6'
M6
0,j
0,'1'
0,h1
4,j
4,'-6'
4,'2'
0,feld(4)
4,h1
4,'-6'
4,'2'
0,feld(4)
M6
M4
i
j
hilf
feld
h1
BNL
L
S
M
L
ST
L
S
M
L
L
S
M
ST
L
L
S
M
ST
L
S
ST
B
L
A
ST
B
EOJ
DS
DS
DS
DS
DS
END
M6
4,j
4,'-6'
4,'2'
0,feld(4)
0,hilf
4,h1
4,'-6'
4,'2'
0,feld(4)
4,j
4,'-6'
4,'2'
0,feld(4)
0,hilf
4,h1
4,'-6'
4,'2'
0,feld(4)
0,j
0,1
0,j
M5
0,i
0,'1'
0,i
M3
F
F
F
9F
F
InsSort