Grundwissen Jahrgangsstufe 9 Lösungen 144 6 + = ( + )² 144 +

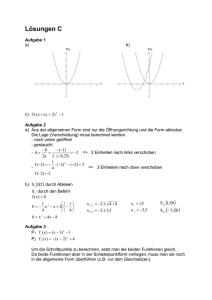
Grundwissen Jahrgangsstufe 9
Lösungen
Berechne ohne Taschenrechner:
a) −√2,25 + √7
1
9
a) = -1,5 +√
9
6
16
6
=
7
6
4
√81𝑎8
Gib die Lösungsmenge der folgenden Gleichungen an:
a) (√𝑥)² = 9
b) -x² = -5
c) 2x² + 50 = 0
Sind folgende Gleichungen richtig oder falsch?
Begründe.
𝑎
a)
= √𝑎
für a > 0
a) 𝐿 = {9}
b) 𝐿 = {−√5; √5}
c) 𝐿 ={ }
a) Wahr, da
2
b) (√√𝑎²) = 𝑎
+
=(
𝑎
√𝑎
=
𝑎∙√𝑎
√𝑎∙√𝑎
=
𝑎∙√𝑎
𝑎
= √𝑎
b) Falsch z. B. a = −1
für 𝑎 ∈ ℝ
c) √𝑎² − 𝑏² = 𝑎 − 𝑏 für 0 < b < a
Berechne die Kantenlänge x eines Würfels mit einem
Volumen von 512 Liter.
Vervollständige die Lücken so, dass sich eine
binomische Formel ergibt:
144𝑐 6
8
3
c) = √3 ∙ 3 ∙ 3 ∙ 3 ∙ 𝑎² ∙ 𝑎² ∙ 𝑎² ∙ 𝑎² = 3𝑎²
4
√𝑎
3
2
=− + =− +
b) = √4 ∙ 4 ∙ 1000 ∙ 1000 = 4 ∙ 1000 = 4000
b) √16 000 000
c)
64
9
1
+ 2 𝑑)²
Verwandle in eine Summe bzw. Differenz:
3
a) (2 𝑥² + 3)²
b) (√2 - 4x)²
Verwandle in ein Produkt:
a) 3p² - 6pv + 3v²
4
4
b) 9 𝑥² + y² + 3 𝑦𝑥
c) Falsch z. B. a = 4 und b = 2: √16 − 4 = √12 ≠ 2
3
x = √512𝑑𝑚³ = 8𝑑𝑚
1
𝑑²
4
144𝑐 6 + 12c³d +
=(
12c³
1
+ 2 𝑑)²
9
a) = 4 𝑥 4 + 9𝑥² + 9
b) = 2 − 8√2𝑥 + 16𝑥²
a) = 3 (p - v)2 = (√3𝑝 − √3𝑣)²
2
b) = ( 𝑥 + 𝑦)²
3
Vereinfache mit Hilfe der Potenzgesetze und gib das
Ergebnis als Wurzel an:
3
1
1
1
3
b) 𝑥 2 ∙ 𝑥 −0,25 ∶ 𝑥 − 4
2
41
3
3
a) (√𝑥 4 )2 = 𝑥 3∙2 = √𝑥²
a) (√𝑥 4 )2
2
c) 4𝑛 ∶ 2𝑛
6
d) √ √ℎ− 3
1 1 3
b) …= 𝑥 2−4+4 = 𝑥
2
𝑛
c) … = (4: 2)𝑛 = √4
31
1
d) …= ℎ−2∙6 = ℎ−4 =
1
4
√ℎ
Bestimme im unten stehenden Dreieck mit einem
rechten Winkel bei C sin𝛼, cos𝛼, tan𝛼, sin𝛽, cos𝛽 und
tan𝛽.
Sinus und Kosinus am Einheitskreis
Welche der Aussagen sind wahr? Begründe.
a) sin0° < sin15°
b) cos90° > sin0°
a) Wahr, da sich mit wachsendem Winkel die
Sinuswerte erhöhen (bis 90°)
b) Falsch, da cos90° = 0; sin 0° = 0;
also gilt cos90° = sin0°!
Eine Leiter der Länge 7,5 m lehnt in der
Höhe 6,6 m an einer Hauswand.
Bestimme den Winkel 𝛼 und wie weit das
untere Ende der Leiter von der Hauswand
entfernt ist.
15
Berechne sin𝛼, wenn gilt cos𝛼 = 17
Ein Tetraeder-Würfel wird zweimal
geworfen und jedes Mal die Ziffer notiert,
die auf der Unterseite steht.
a) Gib die Ergebnismenge Ω an.
b) Schreibe folgende Ereignisse als Menge:
A: Es wird zwei Mal dieselbe Zahl gewürfelt
B: Es wird mindestens einmal eine 1
gewürfelt.
c) Bestimme P(A) und P(B)
Aus einer Urne mit zwei weißen und drei roten Kugeln
werden nacheinander drei Kugeln ohne zurücklegen
gezogen. Zeichne ein passendes Baumdiagramm und
lies ab.
a) Gib die Wahrscheinlichkeit an, mit der man
zuerst eine weiße Kugel zieht.
b) Gib die Wahrscheinlichkeit an, mit der man
zwei weiße Kugeln und eine rote Kugel zieht.
c) Gib die Wahrscheinlichkeit an, mit der man
beim zweiten Zug eine weiße Kugel zieht.
sin𝛼 =
6,6𝑚
7,5𝑚
= 0,88 ⇒ 𝛼 ≈ 61,6°
√(7,5m)² − (6,6m)² ≈ 3,6𝑚
8
sin²𝛼 + 𝑐𝑜𝑠²𝛼 = 1 ⇒ sin𝛼 = √1 − 𝑐𝑜𝑠²𝛼 = 17
a) Ω =
{(1; 1), (1; 2), (1; 3), (1; 4), (2; 1), (2; 2), (2; 3),
(2; 4), (3; 1), (3; 2), (3; 3), (3; 4), (4; 1), (4; 2), (4; 3),
(4;4)}
b) A = {(1;1),(2;2),(3;3),(4;4)}
B = {(1; 1), (1; 2), (1; 3), (1; 4), (2; 1), (3; 1), (4; 1)}
1
7
c) P(A) = 4 , P(B) = 16
2
a) P(„erste Kugel weiß“) = 5
b) Günstig sind die Ziehungen wwr, wrw und rww
P(„zwei Kugeln weiß, eine Kugel rot“)
2 1
2 3 1
3 1 1
= 5 ∙ 4 ∙ 1 + 5 ∙ 4 ∙ 3 + 5 ∙ 2 ∙ 3 = 0,3
c) Günstig sind die Ziehungen ww und rw (der 3. Zug spielt
keine Rolle)
2 1
3 2
4
2
P(„zweite Kugel weiß“) = ∙ + ∙ = =
5 4
a) Ergänze die fehlenden Wahrscheinlichkeiten
im folgenden Baumdiagramm, das zu einem
Urnenexperiment gehört.
b) Beschreibe ein dazu passendes
Urnenexperiment
Berechne die Längen der Seiten a und c sowie die
Höhe h für ein rechtwinkliges Dreieck ABC mit
Hypotenuse c, der Seite b = 9,6 cm und
Hypotenusenabschnitt q = 4,8 cm.
Berechne die Länge des Seite c für ein rechtwinkliges
Dreieck ABC mit = 90°, a = 7,3 cm und b = 4,7cm.
5 4
10
5
a)
b) In einer Urne befinden sich 8 Kugeln. Fünf gelbe,
zwei rote und eine blaue Kugeln. Es wird zweimal
ohne Zurücklegen gezogen.
Kathetensatz: 𝑏 2 = 𝑐 ∙ 𝑞 => 𝑐 =
𝑏2
𝑞
=> 𝑐 = 19,2 𝑐𝑚;
 p = c – q = 14,4 cm;
 𝑎 = √𝑐 ∙ 𝑝 ≈ 16,6 𝑐𝑚; (Kathetensatz)
 ℎ = √𝑝 ∙ 𝑞 ≈ 8,3 𝑐𝑚; (Höhensatz)
= 90° => a ist Hypotenuse des Dreiecks
Also gilt:
𝑎2 = 𝑏 2 + 𝑐 2
𝑐 = √𝑎2 − 𝑏 2
𝑐 ≈ 5,6 𝑐𝑚;
Konstruiere mit Hilfe des Höhensatzes
(Kathetensatzes) eine Strecke der Länge √12 cm.
Höhensatz: ℎ2 = 𝑝 ∙ 𝑞
Man wählt z.B. für p = 4 cm und für q = 3 cm,
also gilt: ℎ2 = 4𝑐𝑚 ∙ 3𝑐𝑚 = 12𝑐𝑚2 => ℎ = √12 𝑐𝑚
Konstruktion:
1. Strecke c mit den oben genannten
Hypotenusenabschnitten p = 4 cm und q = 3 cm
2. Thaleskreis um die Strecke c geschnitten mit dem
Lot auf c durch den Punkt L (Höhenfußpunkt) ergibt
den Punkt C
3. Die Strecke ℎ = 𝐿𝐶 = √12 𝑐𝑚
Verwandle das untenstehende Rechteck durch eine
geeignete Konstruktion mit Hilfe des Kathetensatzes
(Höhensatzes) in ein flächengleiches Quadrat.
Kathetensatz: z.B.: 𝑏 2 = 𝑐 ∙ 𝑞
Man trägt zunächst die kürzere Seite des Rechtecks nach
innen ab (im Bild Punkt L), so dass die längere Seite in zwei
Abschnitte (Hypotenusenabschnitte) geteilt wird. Der Punkt
C (siehe Abb.)) liegt dann auf:
1. Lot auf die Längere Seite des Rechtecks durch den
Punkt L
2. Thaleskreis um die längere Seite des Rechtecks
Die Strecke b = [AC] (siehe Abb.) hat dann nach dem oben
genannten Kathetensatz die Länge der Seite des gesuchten
Quadrats.
Gegeben ist ein Dreieck ABC, von dem die Seitenlängen a = 13 cm, b = 12 cm und c = 4 cm bekannt sind.
Entscheide durch Rechnung, ob es dabei um ein
rechtwinkliges Dreieck handelt!
Wegen a2 ≠ b2 + c2 (Kehrsatz des Satzes von Pythagoras) ist
das Dreieck nicht rechtwinklig!
Berechne die Kantenlänge s sowie den
Oberflächeninhalt O der unten abgebildeten
Pyramide mit quadratischer Grundfläche G mit
Seitenlänge a = 6,0 cm und der Höhe h = 8,0 cm.
Für O gilt: 𝑂 = 𝐺 + 4 ∙ 𝑆 = 𝑎2 + 4 ∙ 0,5 ∙ 𝑎 ∙ ℎ𝑆𝑒𝑖𝑡𝑒𝑛𝑓𝑙ä𝑐ℎ𝑒 =
𝑎 2
= 𝑎2 + 2 ∙ 𝑎 ∙ √( ) + ℎ2 = 36𝑐𝑚2 + 12√73𝑐𝑚2
2
≈ 139 𝑐𝑚2
𝑎 2
Für s gilt: 𝑠 2 = ℎ2 + (√2 ∙ 2 ) = ℎ2 + 2 ∙
 𝑠 = √(8𝑐𝑚)2 +
(6𝑐𝑚)2
2
𝑎2
4
= ℎ2 +
𝑎2
;
2
= √82𝑐𝑚 ≈ 9,1𝑐𝑚;
hSeitenfläche
𝑎 2
√2 ∙ ( )
2
Eine zylindrische Litfaßsäule ist 3,20 m hoch. Sie hat
einen Außendurchmesser von d = 14 dm. Wie groß ist
die Fläche, die beklebt werden kann?
Eine zylinderförmige Regentonne hat einen Innendurchmesser von 8,0 dm und eine Höhe von 1,10 m.
a) Wie viel Regenwasser passt maximal in die
Tonne?
MZylinder = 2 ∙ 𝜋 ∙ 𝑟 ∙ ℎ = 𝜋 ∙ 𝑑 ∙ ℎ ≈ 14,1 𝑚2
a) VZylinder = 𝐺 ∙ ℎ = 𝜋 ∙ 𝑟 2 ∙ ℎ = 176 𝜋 𝑑𝑚3 ≈ 553𝑑𝑚3
b) 𝑉𝑍𝑦𝑙 = 𝜋 ∙ 𝑟 2 ∙ ℎ
𝑉
b) Bis zu welcher Höhe ist die Tonne gefüllt,
wenn 180 Liter in ihr enthalten sind?
Stelle eine Gleichung für den Oberflächeninhalt O
eines Tetraeders in Abhängigkeit seiner Kantenlänge a
auf. (siehe Abbildung unten)
180𝑑𝑚3
 ℎ = 𝜋𝑟2 = 𝜋∙(4𝑑𝑚)2 ≈ 3,6 𝑑𝑚
𝑎 2
𝑎
𝑂 = 4 ∙ 0,5 ∙ 𝑎 ∙ √𝑎2 − ( ) = 2 ∙ 𝑎 ∙ √3 = 𝑎2 √3
2
2
Ein kegelförmiges Sektglas hat den Randdurchmesser
6 cm und eine Höhe von 15 cm.
Wie viel Prozent des Gesamtvolumens sind enthalten,
wenn es bis zur halben Höhe gefüllt ist.
1 21
𝑉𝐹𝑙ü𝑠𝑠𝑖𝑔𝑘𝑒𝑖𝑡 3 𝜋𝑟 2 ℎ 1 𝑟 2 1 𝑟 2 1 1,5 2
=
= ∙ 2 = ∙( ) = ∙( ) =
1 2
𝑉𝑔𝑒𝑠𝑎𝑚𝑡
2 𝑅
2 𝑅
2
3
𝜋𝑅 ℎ
3
= 12,5%
Gegeben ist die Funktion f(x) = −(x + 2)2 + 5.
Welche Aussagen lassen sich (ohne weitere
Rechnung) über den Graphen dieser Funktion
machen?
Eine Normalparabel mit dem Scheitel S(0∣0) hat
die Gleichung y = x2; diese Parabel wird nun um
drei Einheiten nach rechts und um zwei Einheiten
nach oben verschoben. Wie lautet die neue
Funktionsgleichung? - Bringe diese auch auf die
Form y = ax2 + bx + c!
Der Graph ist eine nach unten geöffnete
Normalparabel mit dem Scheitel S(−2∣5)!
y = (x − 3)2 + 2 (Scheitelform) ergibt umgeformt:
y = x2 − 6x + 11
Gegeben ist die Parabel p durch den
Funktionsterm p(x) = −3x2 + 12x + 9.
a) Bestimme den Scheitelpunkt der Parabel p!
b) Bestimme ohne Rechnung die Anzahl der
Nullstellen der Funktion p!
Bestimme die Anzahl der Nullstellen folgender
Parabeln:
a) f(x) = 7(x + 5)2 − 2016
b) g(x) = 0,125x2 + 17
c) h(x) = 5x2 − 2x + 3.
Gegeben ist die quadratische Funktion durch den
Term f(x) = −x2 + 3x + 4.
a) Berechne die Lösungen der quadratischen
Gleichung −x2 + 3x + 4 = 0.
b) Welche geometrische Bedeutung haben die
Lösungen für die quadratische Funktion?
c) Liegt der Scheitelpunkt des Graphen Gf unteroder oberhalb der x-Achse? - Begründe deine
Antwort ohne den Scheitelpunkt zu
bestimmen!
a) mittels quadratischer Ergänzung erhält man den
umgeformten Funktionsterm p(x) = −3⋅ (x −2)2 + 21;
also liegt der Scheitel bei S(2∣21)!
b) Da der Scheitel oberhalb der x-Achse liegt und die
Parabel nach unten geöffnet ist, muss es zwei
Nullstellen geben!
a) Die Parabel ist nach oben geöffnet und der Scheitel
S(−5∣−2016) liegt unterhalb der x-Achse; damit zwei
Nullstellen!
b) Die Parabel ist nach oben geöffnet und der Scheitel
S(0∣17) liegt oberhalb der x-Achse; damit keine
Nullstelle!
c) Die Diskriminante D hat den Wert D = b2 − 4ac =
= (−2)2 − 4 ⋅ 5 ⋅ 3 = −54 < 0;
damit gibt es keine Nullstellen!
a) z. B. mit „Mitternachtsformel” : x1 = −1 und x2 = 4!
b) Es wurden die Schnittpunkte des Graphen Gf mit der
x-Achse (y = 0) bestimmt; die Lösungen sind daher
die Nullstellen der Funktion f!
c) Die Parabel ist nach unten geöffnet; außerdem
besitzt die Funktion zwei Nullstellen. Daher muss
der Scheitel oberhalb der x-Achse liegen!
Die rechte Abbildung zeigt eine zur Normalparabel kongruente Parabel mit der Gleichung y = f(x)
a) Gib einen passenden Term für f(x) an!
b) Zeichne die Gerade mit der Gleichung
3
y = 2 − x in die Abbildung ein!
2
c) Beschreibe, wie man rechnerisch die
Koordinaten der Punkte bestimmen kann, in
denen sich die Parabel und die Gerade
schneiden!
a) y = 5 − x2 .
b) Geradengleichung y = mx + t: d. h. m = −1,5 („2
nach rechts und 3 nach unten”) und yAchsenabschnitt t = 2 verwenden!
c) Die beiden x-Koordinaten der Schnittpunkte erhält
man durch Lösen der Gleichung 5 − x2 = 2 −1,5 x; die
y-Koordinaten durch Einsetzen der beiden Lösungen
in den Funktionsterm f(x)!
Eine Parabel wird durch die Funktionsgleichung
y = −0,5(x − 2)2 + 4 beschrieben. Entscheide, ob
die folgenden Aussagen richtig oder falsch sind!
- Die Parabel ist symmetrisch zur Geraden y = 2.
- Die Parabel schneidet die y-Achse im Punkt
P(0∣2).
- Die Parabel enthält den Punkt Q(6∣−10).
- Die Parabel verläuft für x < −2 unterhalb der xAchse.
- Die Parabel schneidet die x-Achse nicht.
Bestimme die Lösungsmenge der folgenden
Gleichung:
x4 − 7x2 − 18 = 0
-
falsch (x = 2)
richtig
-
falsch (denn f(6) = −4)
richtig
-
falsch (zwei Nullstellen!)
Mit der Substitution u := x2 ergibt sich die quadratische
Gleichung u2 − 7u − 18 = 0;
deren Lösungen sind u1 = −2 und u2 = 9.
Durch Resubstituieren (u1 = −2 = x2 nicht lösbar!)
ergeben als Lösung der Ausgangsgleichung −3 und +3!