3.3-1 „Änderung der Bilanzgr

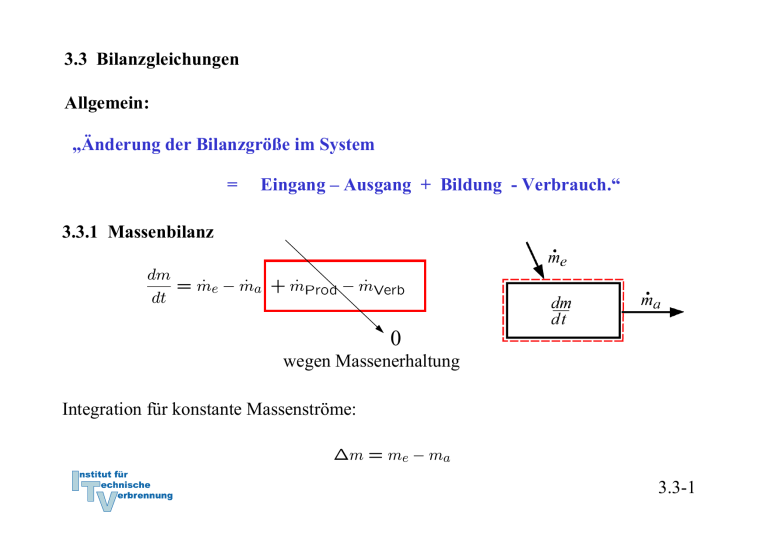
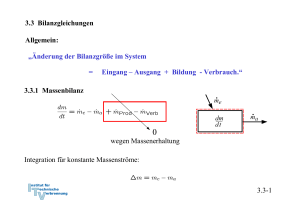
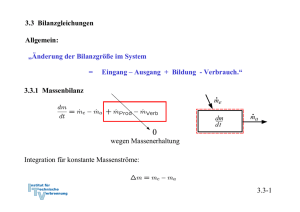
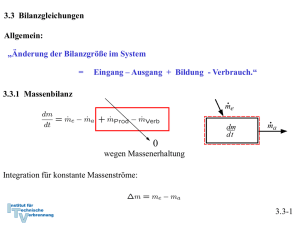
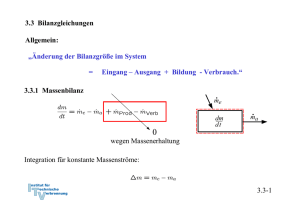
3.3 Bilanzgleichungen
Allgemein:
„Änderung der Bilanzgröße im System
=
Eingang – Ausgang + Bildung - Verbrauch.“
3.3.1 Massenbilanz
0
wegen Massenerhaltung
Integration für konstante Massenströme:
3.3-1
3.3.2 Energiebilanz und 1. Hauptsatz der Thermodynamik
0
wegen Energieerhaltung
oder
1. Hauptsatz der
Thermodynamik
Integration:
Zustandsänderung
Arbeit, Wärme, mit Massenstrom mitgeführte Energie
3.3-2
Verschiedene Schreibweisen
Integrale Form:
Ratenform:
Massenbezogene integrale Form:
Massenbezogene differentielle Form:
Formulierung der Energiebilanz:
1.
Geschlossenes oder offenes System
2.
Absolut- oder Ratenform
3.
Spezifisch oder Massenform
3.3-3
Energiebilanz in geschlossenen Systemen
Zustandsänderung
Zustandsänderung 1 → 2
oder
bzw.
3.3-4
Beispiel 1: Wasserdampf in Zylinder
m = 5 kg
p1 = 500 kPa, ϑ1 = 200 oC
p2 = p1 = 500 kPa, ϑ2 = 120 oC
Wie groß ist die ausgetauschte Wärmemenge Q12?
Skizze im T,v – Diagramm!
Lösung:
1. Hauptsatz:
da
3.3-5
Zustand 1 überhitzt
Zustand 2 unterkühlt
Tabelle Überhitzter Dampf
Inkompressible Flüssigkeit, Sättigungstabelle
3.3-6
Skizze im T,v - Diagramm
3.3-7
Näherung:
u’ (ϑ2) = 503,5 kJ/kg, v’ (ϑ2) = 0,00106 m3/kg
Sättigungsenthalpie gute Näherung, aber
( h’(ϑ2) = 503,71 kJ/kg )
oft nicht genau genug.
h2 (ϑ2) = 504,03 kJ/kg
3.3-8
h1 = 2855,4 kJ/kg
Q12 = m (h2-h1) = 5 kg ( 2855,4 kJ/kg - 504,03 kJ/kg ) ≅ - 11757 kJ
3.3-9
Beispiel 2: Kolben-Zylindersystem im Schwerefeld der Erde
Ein Kolben mit Masse mK schließt einen mit Gas,
Masse mG, gefüllten Zylinder nach oben ab.
Der Kolben werde ein kleines Stück dz langsam nach oben
bewegt, so dass das Gas im Inneren stets im Gleichgewicht sei.
Der Kolben gleite ferner reibungsfrei.
Formulieren Sie die differenzielle Energiebilanz für diesen Prozess!
Lösung:
Der 1. Hauptsatz für ein geschlossenes System mit Änderung äußerer Energien lautet allgemein:
3.3-10
Nebenstehend sind zwei mögliche Systemabgrenzungen skizziert.
Für beide Systeme sollen die Bilanzen formuliert werden.
Für beide Systeme wird der Vorgang als langsam angenommen,
so dass diese stets im Gleichgewicht stehen.
Die Systeme besitzen dann keine kinetische Energie.
Weiterhin wird angenommen, dass der Kolben
reibungslos gleite.
3.3-11
Die Bilanz lautet unter diesen Voraussetzungen für beide Systeme:
System 1:
Bei Verschiebung der oberen Grenze gewinnt das Gas die
potentielle Energie. Damit ist die Arbeit der Gewichtskraft bei der
Verschiebung des Schwerpunkts erfasst.:
Die Volumenänderungsarbeit ist:
Die Bilanz für System 1 lautet also:
3.3-12
System 2:
Bei Verschiebung der oberen Grenze gewinnen das Gas und der
Kolben die potentielle Energie:
Die Volumenänderungsarbeit ist Verschiebearbeit gegen die
Umgebung:
Die resultierende äußere Kraft
leistet die Arbeit:
Die Bilanz für System 2 lautet also:
Wegen der hydrostatischen Aussage
folgt wieder wie für System 1:
3.3-13
3.3.3 Spezifische Wärmekapazitäten
Spezifische Wärmekapazitäten bei konstantem Volumen: cv
Änderung der Inneren Energie:
Definition der spezifischen Wärmekapazität bei konstantem Volumen:
Zur Bestimmung der Änderung der Inneren Energie auf Grund einer
Temperaturänderung ist es zweckmäßig isochore Prozesse zu betrachten.
Dann gilt:
Mit dem 1. Hauptsatz du = δq folgt
cv ist die spezifische Wärme, die zugeführt werden muss, um die Temperatur im
System bei konstantem Volumen um 1 K zu erhöhen.
3.3-14
Bei konstantem Volumen gilt:
Bemerkung:
Wir haben die Änderung der inneren Energie mit der zugeführten Wärme
gekoppelt, indem wir einen isochoren Prozess betrachtet haben:
Für ideale Gase ist die Einschränkung auf einen isochoren Prozess aber nicht
notwendig, da hier wegen
gilt und damit immer:
Der 1. Hauptsatz liefert für ideale Gase:
3.3-15
Spezifische Wärmekapazität bei konstantem Druck: cp
Änderung der Enthalpie:
Definition der spezifischen Wärmekapazität bei konstantem Volumen:
Zur Bestimmung der Änderung der Enthalpie auf Grund einer
Temperaturänderung ist es zweckmäßig isobare Prozesse zu betrachten.
Dann gilt:
3.3-16
Isobarer Prozess:
1. Hauptsatz
isobar
Mit
folgt
und
cp ist die spezifische Wärme, die zugeführt werden muss, um die Temperatur
im System bei konstantem Druck um 1 K zu erhöhen.
3.3-17
Bei konstantem Druck gilt:
Bemerkung:
Wir haben die Änderung der inneren Energie mit der zugeführten Wärme
gekoppelt, indem wir einen isobaren Prozess betrachtet haben:
Für ideale Gase ist die Einschränkung auf einen isochoren Prozess aber nicht
notwendig, da hier wegen
gilt und damit immer:
Der 1. Hauptsatz liefert für ideale Gase:
3.3-18
Spezifische Wärmekapazitäten idealer Gase
Bei idealen Gasen sind die innere Energie und die Enthalpie ausschließlich
Funktionen der Temperatur.
Daher müssen auch die molaren und spezifischen Wärmekapazitäten reine
Temperaturfunktionen sein:
Es gilt ferner:
3.3-19
Ableitung
Ebenso
Verhältnis der spezifischen Wärmen: κ ∗)
Es ergibt sich:
Das Billardkugelmodell des idealen Gases beschreibt im angegebenen Temperaturbereich den Wert für einatomige Gase richtig (vergl. 3.2-26):
Verhältnis der spezifischen Wärmen κ spielt eine besondere Rolle. Wir werden sehen, dass für die
idealen Gase κ gleich dem Isentropenxponenten k ist.
*) Das
3.3-20
Das Verhältnis der spezifischen oder der molaren Wärmen
nimmt bei Umgebungstemperatur näherungsweise folgende Zahlenwerte an:
Einatomige Gase:
κ = 5/3 = 1,66
Zweiatomige Gase: κ = 7/5 = 1,4
3.3-21
Für mehratomige Gase zeigen Messungen, dass die spezifischen Wärmekapazitäten
deutlich größer und deutlich temperaturabhängig sind:
Für zweiatomige Gase bei Raumtemperatur liest man im vorstehenden Diagramm
folgenden Wert ab:
Zweiatomige Gase können bei diesen Temperaturen noch als starres Hantelmodell
dargestellt werden. Da die innere Energie als die Summe der Energien der frei
betrachteten Moleküle dargestellt werden kann, kommt bei zweiatomigen Gasen zu
den drei Energieanteilen der Translation des Billardkugelmodell noch die
Rotationsenergie um zwei Achsen hinzu.
Nach dem Gleichverteilungssatz erhält im statistischen Mittel jeder Freiheitsgrad
die gleiche innere Energie. Daher ist:
Noch höhere Temperaturen regen Molekülschwingungen und bisher eingefrorene
Freiheitsgrade an, so dass die Wärmekapazitäten mit der Temperatur weiter ansteigen.
3.3-22
Translatorische und rotatorische Freiheitsgrade
Einatomige Gase (Beispiel Edelgase wie He, Ar etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
alle eingefroren*)
Zweiatomige Gase (Beispiel Gase wie N2, O2 etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
2 (einer eingefroren*))
Dreiatomige Gase mit gewinkelter Struktur
(Beispiel Gase wie H2O, SO2 etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
3
Aus den Messwerten lässt sich deshalb folgern, dass CO2 keine
gewinkelte Struktur wie H2O oder SO2 hat!
*) Die Tatsache, dass einige rotatorische Freiheitsgrade eingefroren sind, ist ein quantenmechanischer Effekt und lässt sich
mit der klassischen Physik nicht erklären. Die Quantisierung des Drehimpulses erfordert bei kleinem Trägheitsmoment eine
ausreichend hohe Temperatur, um die Rotation um die entsprechende Achse anzuregen. Alle klassischen Erklärungen
widersprechen dem Gleichverteilungssatz, nachdem jeder Freiheitsgrad die gleiche Energie aufnimmt.
3.3-23
Spezifische Wärmekapazitäten idealer Flüssigkeiten
Annahme: inkompressibel, d. h. konstantes Volumen: dv = 0
1. Hauptsatz liefert mit pdv = 0:
Die innere Energie für ideale Flüssigkeiten ist also nur
von der Temperatur abhängig.
3.3-24
Folgerung für die Enthalpie idealer Flüssigkeiten und cp
Definition der Enthalpie:
Vollständiges Differential:
Vergleich:
⇒ Wärmekapazitäten cp und cv sind gleich für ideale Flüssigkeiten.
Die Enthalpie für ideale Flüssigkeiten ist also von der Temperatur und
vom Druck abhängig:
3.3-25
3.3.4 Bewertung von thermodynamischen Prozessen
Generell: Vergleich von Nutzen zu Aufwand
• bei Arbeitsmaschinen → thermischer Wirkungsgrad ηth
• bei Kühlprozessen und Wärmepumpen: → Leistungszahl ε
3.3-26
Beispiel: Otto-Motor
Viertaktmotoren (schematisch)
3.3-27
Der idealisierte Otto-Prozess (Gleichraumprozess)
•
Vernachlässigung von Verlusten ↔ Annahme eines reversiblen Prozesse
•
Massenaustausch mit der Umgebung (Ein- und Ausschieben) bleibt
unberücksichtigt
•
die mit der Materie transportierte Energie wird durch Wärmeabfuhr ersetzt
•
Kompression und Expansion werden als reversibel-adiabate Prozesse
aufgefasst.
•
Wärmezufuhr und Wärmeabfuhr erfolgen bei konstantem Volumen.
3.3-28
Darstellung im p,V-Diagramm
Wirkungsgrad:
3.3-29
Darstellung im T,pvk-Diagramm
Wirkungsgrad:
3.3-30
Bilanz des Kreisprozesses
Volumenänderungsarbeiten
Wärmezufuhr und –abfuhr
3.3-31
Thermischer Wirkungsgrad
Bestimmung der Temperaturverhältnisse:
analog
.
.
.
3.3-32
Thermischer Wirkungsgrad des idealisierten Otto-Prozesses
Der Wirkungsgrad steigt mit dem Verdichtungsverhältnis ε an.
*) Werden Wärmeverluste bei Kompression und Expansion und andere Verluste berücksichtigt, so
kann statt des Isentropenexponenten k auch ein adäquater Polytropenexponent n verwendet werden.
3.3-33
3.3.4 Stationärer Fließprozess in offenen Systemen
Annahmen:
Stationär → Masse und Gesamtenergie im System konstant:
3.3-34
Bilanz am stationären offenen System:
3.3-35
Beispiel: Kühlschrank
Gesamtsystem
1. Hauptsatz geschlossenes System, stationär:
Prozessbewertung durch Leistungszahl:
3.3-36
Bilanz am Kompressor:
System Kompressor
1. Hauptsatz offenes System, stationär und adiabat:
Annahme Δekin = Δepot ≅ 0 :
3.3-37
Bilanz am Verdampfer:
System Verdampfer
1. Hauptsatz offenes System, stationär:
Annahme Δekin = Δepot ≅ 0 :
⇒ Leistungszahl:
3.3-38
Bilanz am Kondensator:
Gesamtsystem
System Kondensator
Aus Bilanz am Gesamtsystem, stationär
oder 1. Hauptsatz offenes System, stationär, Δekin = Δepot ≅ 0 :
( Es folgt:
)
3.3-39
Bilanz an der Drossel:
System Drossel
1. Hauptsatz offenes System, stationär, adiabat, Δekin = Δepot ≅ 0 :
Eine adiabate Drossel ist isenthalp!
3.3-40
T,v - Diagramm:
•
In der Drossel soll mit dem Druck auch die Temperatur absinken → Kühlmittel μ > 0
(siehe Joule-Thomson-Koeffizient (Thermodynamik II):
•
Die Drücke p1 und p2 werden so gewählt, dass
T3 > TRaum
T4 < TKühlschrank
3.3-41
Kühlmittel R – 134a
Aus Tabellen:
h1 = 231,4 kJ/kg
h2 = 280,2 kJ/kg
h3 = h4 = 105,3 kJ/kg
⇒ ε = 2,58
• Die Kühlleistung ist damit um einen Faktor 2,58 höher als die eingesetzte Leistung !
• Energie wird zur Verschiebung der thermischen Energie eingesetzt.
3.3-42
Beispiel: Elektrische Heizung
1. Hauptsatz geschlossenes System
Leistungszahl:
Heizung mit Strom ineffizient, da Wirkungsgrad der Stromerzeugung im Kraftwerk
ηKW ≅ 40 %, so dass Gesamtleistungszahl
3.3-43
Beispiel: Konventionelle Heizung
Wärmeleistung
aus chemischer Energie
1. Hauptsatz geschlossenes System
für stationäre Verhältnisse im Haus
(In der Heizung wird gespeicherte chemische Energie in Wärme überführt ⇒ dEH/dt ≠ 0.)
Leistungszahl:
3.3-44
Beispiel: Heizung mit elektrischer Wärmepumpe
Wärmeleistung
aus chemischer Energie
1. Hauptsatz geschlossenes System
für stationäre Verhältnisse im Haus
Leistungszahl:
Mit Zahlenwert für Kühlschrank:
Berücksichtigung der Stromerzeugung:
3.3-45