Balancierte binäre Suchbäume

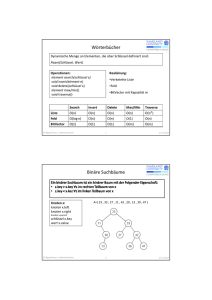
12. Balancierte binäre Suchbäume
Binäre Suchbäume:
• Ausgabe aller Elemente in O(n)
• Suche, Minimum, Maximum, Nachfolger in O(h)
• Einfügen, Löschen in O(h)
Frage:
• Wie kann man eine „kleine“ Höhe unter Einfügen und
Löschen garantieren?
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
1
Balancierte binäre Suchbäume
AVL-Bäume
• Ein Baum heißt AVL-Baum, wenn für jeden Knoten gilt:
Die Höhe seines linken und rechten Teilbaums
unterscheidet sich höchstens um 1.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
2
Balancierte binäre Suchbäume
Satz 12.1
Für jeden AVL-Baum der Höhe h mit n Knoten gilt:
(3/2) h ≤ n ≤ 2h+1 -1
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
3
Balancierte binäre Suchbäume
Satz 12.1
Für jeden AVL-Baum der Höhe h mit n Knoten gilt:
(3/2) h ≤ n ≤ 2h+1 -1
Beweis: Tafel
Korollar 12.2
Ein AVL-Baum mit n Knoten hat Höhe Θ(log n).
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
4
Balancierte binäre Suchbäume
Dynamische AVL-Bäume
• Operationen Suche, Einfügen, Löschen, Min/Max,
Vorgänger/Nachfolger,… wie für binäre Suchbäume
• Laufzeit O(h) für diese Operationen
• Nur Einfügen/Löschen verändern Struktur des Baums
Problem:
• Wir brauchen Prozedur, um AVL-Eigenschaft nach
Einfügen/Löschen wiederherzustellen.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
5
Balancierte binäre Suchbäume
Dynamische AVL-Bäume
Nach Korollar 12.2 gilt
= Θ(log n)
• Operationen Suche, hEinfügen,
Löschen, Min/Max,
Vorgänger/Nachfolger,… wie für binäre Suchbäume
• Laufzeit O(h) für diese Operationen
• Nur Einfügen/Löschen verändern Struktur des Baums
Problem:
• Wir brauchen Prozedur, um AVL-Eigenschaft nach
Einfügen/Löschen wiederherzustellen.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
6
Balancierte binäre Suchbäume
Rotationen, die Suchbaumeigenschaft bewahren:
y
x
x
C
A
SS 2016
y
Rechtsrotation(T,y)
Linksrotation(T,x)
A
B
B
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
C
7
Balancierte binäre Suchbäume
Beispiel 1:
15
15
21
9
x
7
17
SS 2016
y Rechtsrotation(T,y)
27
19
19
9
7
21 y
17
20
20
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
x
27
8
Balancierte binäre Suchbäume
Beispiel 2:
x
y
21
15
y
21
9
17
20
27
15
27
19
7
SS 2016
x
Linksrotation(T,x)
9
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
19
17
20
9
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7.
else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
10. h[x] ← 1+ max{h[lc[x]],h[rc[x]]}
11. h[y] ← 1+ max{h[lc[y]],h[rc[y]]}
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
10
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7.
else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
10. h[x] ← 1+ max{h[lc[x]],h[rc[x]]}
Im folgenden Beispiel werden die
Zeilen 10 und 11 nicht betrachtet
11. h[y] ← 1+ max{h[lc[y]],h[rc[y]]}
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
11
Balancierte binäre Suchbäume
Annahme: x hat
rechtes Kind.
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
12
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
27
19
7
17
20
13
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
y
17
20
14
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
y
17
20
15
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
y
17
20
16
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
y
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
nil
17
20
17
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
x
15
21
9
y
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
nil
17
20
18
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
root[T]
x
15
21
9
y
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
nil
17
20
19
Balancierte binäre Suchbäume
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
root[T]
x
15
21
9
y
27
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
nil
17
20
20
Balancierte binäre Suchbäume
root[T]
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
nil
21
y
x
15
27
9
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
17
20
21
Balancierte binäre Suchbäume
root[T]
Linksrotation(T,x)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
8. lc[y] ← x
9. p[x] ← y
SS 2016
nil
21
y
x
15
27
9
19
7
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
17
20
22
Balancierte binäre Suchbäume
root[T]
Linksrotation(T,x)
Laufzeit: O(1)
1. y ← rc[x]
2. rc[x] ← lc[y]
3. if lc[y]≠nil then p[lc[y]] ← x
4. p[y] ← p[x]
5. if p[x]=nil then root[T] ← y
9
6. else if x=lc[p[x]] then lc[p[x]] ← y
7. else rc[p[x]] ← y
7
8. lc[y] ← x
9. p[x] ← y
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
nil
21
y
x
15
27
19
17
20
23
Balancierte binäre Suchbäume
Zur Aufrechterhaltung der AVL-Baumeigenschaft
betrachten wir zunächst ein vereinfachtes
Problem.
Definition:
• Ein Baum heißt beinahe-AVL-Baum, wenn die AVLEigenschaft in jedem Knoten außer der Wurzel erfüllt ist
und die Höhen der Unterbäume der Wurzel sich um
höchstens 2 unterscheiden.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
24
Balancierte binäre Suchbäume
Problem:
• Umformen eines beinahe-AVL-Baums in einen AVLBaum mit Hilfe von Rotationen
• O.b.d.A.: Linker Teilbaum der Wurzel höher als der
rechte (Fall für den rechten Teilbaum analog)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
25
Balancierte binäre Suchbäume
Fall 1:
y
x
H-1
C
H
B
H oder
H-1
A
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
26
Balancierte binäre Suchbäume
Fall 1:
y
x
Rechtsrotation(T,y)
y
x
C
H
B
A
H oder
H-1
H-1 H
A
H oder
H-1
H-1
B
C
Korrekter AVL-Baum
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
27
Balancierte binäre Suchbäume
Fall 2:
y
x
H-1
C
H
H-1
A
SS 2016
B
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
28
Balancierte binäre Suchbäume
Fall 2:
y
x
H-1
C
H
H-1
A
SS 2016
B
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
29
Balancierte binäre Suchbäume
Fall 2:
y
x
H-1
C
z
H
H-1
A
H-2
oder
H-1
SS 2016
B‘
B‘‘
H-2
oder
H-1
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
30
Balancierte binäre Suchbäume
Fall 2:
y
y
Linksrotation(T,x)
z
x
H-1
H-1
C
C
x
z
B‘‘
H
H-1
A
H-2
oder
H-1
SS 2016
B‘
B‘‘
H-2
oder H-1
H-1
B‘
A
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
H-2
oder
H-1
H-2
oder
H-1
31
Balancierte binäre Suchbäume
Fall 2:
z
y
Rechtsrotation(T,y)
z
x
y
H-1
C
x
B‘‘
B‘
H-1
A
SS 2016
H-2
oder
H-1
H-2
oder
H-1
B‘
B‘‘
C
A
Korrekter AVL-Baum
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
32
Balancierte binäre Suchbäume
Annahme: beinahe-AVL-Baum mit t=root[T]
Balance(T,t)
1. if h[lc[t]] > h[rc[t]]+1 then
2. if h[lc[lc[t]]]< h[rc[lc[t]]] then
3.
Linksrotation(T,lc[t])
4. Rechtsrotation(T,t)
5. else if h[rc[t]]> h[lc[t]]+1 then
6. if h[rc[rc[t]]]< h[lc[rc[t]] then
7.
Rechtsrotation(T,rc[t])
8. Linksrotation(T,t)
y
x
H-1
C
H
B
H oder
H-1
A
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
33
Balancierte binäre Suchbäume
h gibt Höhe des Teilbaums an. Dies
müssen wir zusätzlich in unserer
Datenstruktur aufrecht erhalten.
Zeiger z undefiniert oder nil: h[z]:=-1
Balance(T,t)
1. if h[lc[t]] > h[rc[t]]+1 then
2. if h[lc[lc[t]]]< h[rc[lc[t]]] then
3.
Linksrotation(T,lc[t])
4. Rechtsrotation(T,t)
5. else if h[rc[t]]> h[lc[t]]+1 then
6. if h[rc[rc[t]]]< h[lc[rc[t]] then
7.
Rechtsrotation(T,rc[t])
8. Linksrotation(T,t)
y
x
H-1
C
H
B
H oder
H-1
A
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
34
Balancierte binäre Suchbäume
Balance(T,t)
1. if h[lc[t]] > h[rc[t]]+1 then
2. if h[lc[lc[t]]]< h[rc[lc[t]]] then
3.
Linksrotation(T,lc[t])
4. Rechtsrotation(T,t)
5. else if h[rc[t]]> h[lc[t]]+1 then
6. if h[rc[rc[t]]]< h[lc[rc[t]] then
7.
Rechtsrotation(T,rc[t])
8. Linksrotation(T,t)
y
x
H-1
C
H
B
H oder
H-1
A
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
35
Balancierte binäre Suchbäume
Balance(T,t)
1. if h[lc[t]] > h[rc[t]]+1 then
2. if h[lc[lc[t]]]< h[rc[lc[t]]] then
3.
Linksrotation(T,lc[t])
4. Rechtsrotation(T,t)
5. else if h[rc[t]]> h[lc[t]]+1 then
6. if h[rc[rc[t]]]< h[lc[rc[t]] then
7.
Rechtsrotation(T,rc[t])
8. Linksrotation(T,t)
x
y
A
B
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
C
36
Balancierte binäre Suchbäume
Balance(T,t)
1. if h[lc[t]] > h[rc[t]]+1 then
2. if h[lc[lc[t]]]< h[rc[lc[t]]] then
3.
Linksrotation(T,lc[t])
4. Rechtsrotation(T,t)
5. else if h[rc[t]]> h[lc[t]]+1 then
6. if h[rc[rc[t]]]< h[lc[rc[t]] then
7.
Rechtsrotation(T,rc[t])
8. Linksrotation(T,t)
Laufzeit: O(1)
x
y
A
B
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
C
37
Balancierte binäre Suchbäume
Kurze Zusammenfassung:
• Wir können aus einem beinahe-AVL-Baum mit Hilfe von
maximal 2 Rotationen einen AVL-Baum machen
• Dabei bleibt die Höhe des Baums gleich oder nimmt um
1 ab (siehe Schaubilder auf Folien 26-32)
Einfügen:
• Wir fügen ein wie früher
• Dann laufen wir den Pfad zur Wurzel zurück
• An jedem Knoten balancieren wir, falls der Unterbaum
ein beinahe-AVL-Baum ist.
• Das ergibt induktiv wieder einen korrekten AVL-Baum.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
38
Balancierte binäre Suchbäume
Aufruf mit AVL-Einfügen(nil,root[T],x)
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
39
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
40
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
41
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
42
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
43
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
44
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Einfügen 2
9
6
45
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
nil
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
46
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t]
thenKnoten
AVL-Einfügen(t,rc[t],x)
Neuen
erzeugen,
Zeiger lc[t]schon
und rc[t]vorhanden
auf
5. else return  Schlüssel
nil setzen, sowie p[t] auf
8
6. h[t] = 1 + max{h[lc[t]],
h[rc[t]]}
p und
den Zeiger (lc oder
5
rc) von p (falls ≠ nil) auf t
7. Balance(T,t)
setzen.
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
47
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
h[nil] definieren wir als -1.
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
48
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
49
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
50
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
51
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
8
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
5
7. Balance(T,t)
3
Einfügen 2
9
6
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
52
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
5
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
3
7. Balance(T,t)
2
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
6
Einfügen 2
8
9
53
Balancierte binäre Suchbäume
AVL-Einfügen(p,t,x)
1. if t=nil then
2. füge x an Position t unter p ein; return
3. else if key[x]<key[t] then AVL-Einfügen(t,lc[t],x)
4. else if key[x]>key[t] then AVL-Einfügen(t,rc[t],x)
5. else return  Schlüssel schon vorhanden
5
6. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
3
7. Balance(T,t)
Laufzeit:
2
6
Einfügen 2
8
9
• O(h) = O(log n)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
54
Balancierte binäre Suchbäume
Korrektheit:
• h(v): Höhe das Baumes mit Wurzel v vor dem Einfügen von x
• h´(v): Höhe das Baumes mit Wurzel v nach dem Einfügen von x
Direkt nach dem Einfügen von x gilt:
• Für alle Knoten v entlang des Suchpfades von x, h´(v)∈{h(v),h(v)+1},
und für alle anderen ist h´(v)=h(v).
• Ist h´(v)=h(v)+1, dann ist auch h´(w)=h(w)+1 für das Kind w von v in
Richtung x (da der andere Teilbaum von v die Höhe beibehalten
hat).
• Da h´(x)=h(x)+1 (an der Position von x war vorher nil, und h(nil)=-1),
gibt es einen Vorfahren v von x mit h´(w)=h(w)+1 für alle Knoten w
entlang des Suchpfades von v nach x, und für alle anderen Knoten
w gilt, h´(w)=h(w).
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
55
Balancierte binäre Suchbäume
Korrektheit:
• h(v): Höhe das Baumes mit Wurzel v vor dem Einfügen
• h´(v): Höhe das Baumes mit Wurzel v nach dem Einfügen
Wir wissen:
• Bei einer Balancierung bleibt die Höhe gleich oder sinkt um 1.
• Es gibt einen Vorfahren v von x mit h´(w)=h(w)+1 für alle Knoten w
entlang des Suchpfades von v nach x, und für alle anderen Knoten
w gilt, h´(w)=h(w).
• Eine Balancierung kann bei w nur dann stattfinden, wenn
h´(w)=h(w)+1 ist (da sonst die AVL-Eigenschaft gilt).
• Sobald zum ersten Mal die Balancierung eines Vorfahrens w von x
ergibt, dass danach h´(w)=h(w) ist, dann korrigieren sich dadurch
auch die Höhen aller anderen Vorfahren y von x über w auf
h´(y)=h(y), so dass keine weiteren Balancierungen mehr notwendig
sind.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
56
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung ist nur genau einmal notwendig.
Beweis:
• Fall 1: einfache Rotation.
Da h´(u)=h(u)+1, muss Höhe von Teilbaum A angewachsen sein,
d.h. für die aktuellen Höhen muss für ein H gelten:
u
Rechtsrotation(T,y)
v
u
v
C
H
A
B
H-1
H-1
H
A
x H-1
B
C
H-1
x
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
57
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung ist nur genau einmal notwendig.
Beweis:
• Fall 1: einfache Rotation.
Da nachher h´(v)=h(u) ist, gibt es keine weiteren Rebalancierungen
mehr.
u
Rechtsrotation(T,y)
v
u
v
C
H
A
B
H-1
H-1
H
A
x H-1
B
C
H-1
x
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
58
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung ist nur genau einmal notwendig.
Beweis:
• Fall 2: Doppelrotation.
Da h´(u)=h(u)+1, muss Höhe von Teilbaum B angewachsen sein,
d.h. für die aktuellen Höhen muss für ein H gelten:
u
w
Doppelrotation
v
v
C
w
H-1
A
B
H
u
H-1
A
B‘
x
B‘‘
C
x
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
59
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung ist nur genau einmal notwendig.
Beweis:
• Fall 2: Doppelrotation.
Da nachher h´(w)=h(u) ist, gibt es auch hier keine weiteren
Rebalancierungen mehr.
u
w
Doppelrotation
v
v
C
w
H-1
A
B
H
u
H-1
A
B‘
x
B‘‘
C
x
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
60
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
5
3
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
61
Balancierte binäre Suchbäume
k bezeichnet Schlüssel
des zu löschenden
Elements.
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
3
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
62
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
3
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
63
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
3
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
64
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
Und die anderen
2. else if k>key then AVL-Löschen(rc[t],l)
Zeiger aktualisieren
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
Löschen(3)
8.
AVL-Löschen(lc[t],key[u])
5
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
8
nil
10.Balance(T,t)
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
65
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
Oder h[t]=-1,
7.
Kopiere Informationen von ufalls
nach
t=nil t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
8
nil
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
66
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
Nichts zu tun,
8.
AVL-Löschen(lc[t],key[u])
da Baum leer.
9. h[t] = 1 + max{h[lc[t]],
h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
8
nil
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
67
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
Löschen(3)
5
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
68
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
5
Löschen(3)
8
9
6
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
69
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
8
9
6
7
70
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
8
9
6
7
71
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
8
9
6
7
72
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
8
9
6
7
73
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
8
9
6
7
74
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
7
75
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch
lc[t]
u hat kein
6. else u=MaximumSuche(lc[t])
rechtes Kind.
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
7
76
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
7
77
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
78
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
79
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
80
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
81
Balancierte binäre Suchbäume
AVL-Löschen(t,k)
1. if k<key[t] then AVL-Löschen(lc[t],k)
2. else if k>key then AVL-Löschen(rc[t],k)
3. else if t=nil then return  k nicht im Baum
4. else if lc[t]=nil then ersetze t durch rc[t]
5. else if rc[t]=nil then ersetze t durch lc[t]
6. else u=MaximumSuche(lc[t])
7.
Kopiere Informationen von u nach t
8.
AVL-Löschen(lc[t],key[u])
2
9. h[t] = 1 + max{h[lc[t]], h[rc[t]]}
10.Balance(T,t)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
Löschen(8)
5
3
7
9
6
82
Balancierte binäre Suchbäume
Korrektheit:
• h(v): Höhe das Baumes mit Wurzel v vor dem Einfügen von x
• h´(v): Höhe das Baumes mit Wurzel v nach dem Einfügen von x
Direkt nach dem Löschen von x (oder einem Nachfahren von x, den wir
in diesem Fall auch mit x bezeichnen) gilt:
• Für alle Knoten v entlang des Suchpfades von der Wurzel zum
Elternknoten y von x gilt h´(v)∈{h(v),h(v)-1}, und für alle anderen ist
h´(v)=h(v).
• Ist h´(v)=h(v)-1, dann ist auch h´(w)=h(w)-1 für das Kind w von v in
Richtung y (da der andere Teilbaum von v die Höhe beibehalten
hat).
• Gilt für den Elternknoten y, dass h´(y)=h(y), muss demnach für alle
Knoten v gelten, dass h´(v)=h(v), und es ist nichts zu rebalancieren.
Wir nehmen daher im folgenden an, dass h´(y)=h(y)-1.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
83
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung bei u ist nur für h´(u)=h(u) möglich.
Beweis:
• Fall 1: einfache Rotation.
Kann nur passieren, wenn sich die Höhe von C verkleinert hat. In
diesem Fall gilt dann aber, dass h´(u)=h(u).
u
Rechtsrotation(T,y)
u
v
x
C
H
A
SS 2016
v
B
H oder
H-1
H-1
H
A
x
H
oder H-1
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
B
C
H-1
84
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung bei u ist nur für h´(u)=h(u) möglich.
Beweis:
• Fall 1: einfache Rotation.
Nach der Rotation ist daher h´(v)={h(u),h(u)-1}.
u
Rechtsrotation(T,y)
u
v
x
C
H
A
SS 2016
v
B
H oder
H-1
H-1
H
A
H
x
oder H-1
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
B
C
H-1
85
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung bei u ist nur für h´(u)=h(u) möglich.
Beweis:
• Fall 2: Doppelrotation.
Kann auch nur passieren, wenn sich die Höhe von C verkleinert hat.
In diesem Fall gilt dann aber, dass h´(u)=h(u).
u
w
Doppelrotation
v
x
C
w
H-1
SS 2016
A
H
B
v
u
H-1
B‘
A
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
B‘‘
C
86
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung bei u ist nur für h´(u)=h(u) möglich.
Beweis:
• Fall 2: Doppelrotation.
Nach der Rotation ist daher h´(w)=h(u)-1.
u
w
Doppelrotation
v
x
C
w
H-1
SS 2016
A
H
B
v
u
H-1
B‘
A
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
B‘‘
C
87
Balancierte binäre Suchbäume
Korrektheit:
Behauptung: Eine Rebalancierung bei u ist nur für h´(u)=h(u) möglich.
Die Fälle im Beweis haben weiterhin gezeigt, dass
• Rotationen nur möglich sind, wenn für einen Knoten u gilt, dass
h´(u)=h(u), während für ein Kind v von u, h´(v)=h(v)-1 ist.
• Weiterhin gilt nach den Rotationen, dass schlimmstenfalls
h´(u)=h´(u)-1 gilt, so dass die Höhendifferenz bei den Vorfahren von
u nicht schlimmer als 2 werden kann.
• Allerdings können im Gegensatz zum Insert beim Remove
logarithmisch viele Rotationen notwendig sein. Da jede Rotation
aber nur konstanten Aufwand hat, ist das nicht weiter schlimm.
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
88
Balancierte binäre Suchbäume
Satz 12.3
Mit Hilfe von AVL-Bäumen kann man Suche, Einfügen,
Löschen, Minimum und Maximum in einer Menge von n
Zahlen in Θ(log n) Laufzeit durchführen.
Zusammenfassung und Ausblick:
• Effiziente Datenstruktur für das Datenbank Problem mit
Hilfe von Suchbäumen
• Kann man eine bessere Datenstruktur finden?
• Was muss man ggf. anders machen?
(untere Schranke für vergleichsbasierte Strukturen)
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
89
Changelog
23.05.16: fast alle Folien ab Folie 33
27.05.16: Folien 57-60 (neu), ab 83 neu oder überarbeitet
SS 2016
Datenstrukturen und Algorithmen
12.Balancierte Binärbäume
90