Ma III - Kapitel Stochastik - MB/ME Regressionsanalyse Beispiel 3

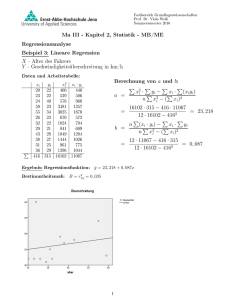
Fachbereich Grundlagenwissenschaften
Prof. Dr. Viola Weiÿ
Sommersemester 2015
Ma III - Kapitel Stochastik - MB/ME
Regressionsanalyse
Beispiel 3: Lineare Regression
X - Alter des Fahrers
Y - Geschwindigkeitsüberschreitung
in km/h
Daten und Arbeitstabelle:
P
xi
yi
x2i
xi · y i
20
22
400
440
23
22
529
506
24
40
576
960
59
23
3481
1357
55
34
3025
1870
26
22
676
572
32
22
1024
704
29
21
841
609
43
28
1849
1204
38
27
1444
1026
31
25
961
775
36
29
1296
1044
416
315
16102
11067
Berechnung von
b:
P 2 P
P
P
xi · yi − xi · (xi yi )
P
P
a =
n x2i − ( xi )2
a
und
16102 · 315 − 416 · 11067
= 23, 218
12 · 16102 − 4162
P
P
P
n (xi · yi ) − xi · yi
P
P
b =
n x2i − ( xi )2
=
=
12 · 11067 − 416 · 315
= 0, 087
12 · 16102 − 4162
Ergebnis: Regressionsfunktion: ŷ = 23, 218 + 0, 087x
2
Bestimmtheitsmaÿ: B = rxy
= 0, 035
1
Elimination des Ausreiÿers (24, 40)
Regressionsfunktion: ŷ = 17, 9718 + 0, 197x
2
= 0, 365
Bestimmtheitsmaÿ: B = rxy
Elimination von zwei Ausreiÿern (24, 40) und (59, 23)
Regressionsfunktion: ŷ = 12, 717 + 0, 375x
2
= 0, 831
Bestimmtheitsmaÿ: B = rxy
2
Beispiel 4: Regressionskurve für eine Exponentialfunktion
Die Entladung eines Kondensators mit Kapazität
nach dem Exponentialgesetz
C
über einen Ohmschen Widerstand
t
u(t) = u0 · e− RC
mit der Anfangsspannung
u0
zur Zeit
t≥0
t = 0.
In einem Experiment wurden folgende Werte gemessen (t in s und
ti
ui
R erfolgt
1,0
4,0
7,0
10,0
15,0
80,2
45,5
24,5
13,9
4,7
Aus diesen Daten sollen die Anfangsspannung
u0
u
in V):
.
und die Zeitkonstante
RC
geschätzt werden.
Des weiteren soll der Zeitpunkt bestimmt werden, wo die Spannung 0,1V unterschreitet.
1
) · t.
Transformation in eine lineare Funktion durch Logarithmieren: ln u = ln u0 + (− RC
Arbeitstabelle:
1
Berechnung von a = ln u0 und b = − RC
:
P
P
ti
ui
ln ui
t2i
1
80,2
4,384524
1
4
45,5
3,817712
16
7
24,5
3,198673
49
10
13,9
2,631889
100
15
4,7
1,547563
225
15,580361
391
37
a =
ti · ln ui
91,578411
t
Regressionsfunktion: û(t) = 100, 84 V · e− 4,94 s
t
=⇒
P
P
ln ui − ti · (ti · ln ui )
P
P
n t2i − ( ti )2
391 · 15, 580361 − 37 · 91, 578411
= 4, 6135
5 · 391 − 372
P
P
P
n (ti · ln ui ) − ti · ln ui
P
P
b =
n t2i − ( ti )2
1
RC = − −0,2024
= 4, 94
0, 1 = 100, 84 V · e− 4,94 s
P
=
=
u0 = e4,6135 = 100, 84
t2i ·
t = 34, 17 s.
3
12 · 91, 578411 − 37 · 15, 580361
= −0, 2024
5 · 391 − 372
Beispiel 5: Logistische Regression
Die folgende Tabelle zeigt die prozentuale Ausstattung von Haushalten einer deutschen Groÿstadt mit Videorecordern:
1992
1993
1994
1995
1996
1997
1998
3
8
19
33
50
63
74
.
Berechnen Sie zur Beschreibung der Entwicklung eine logistische Regressionsfunktion ŷ
mit Sättigungsgrenze
=
k = 80.
Schätzen Sie den Ausstattungsgrad für das Jahr 2000.
Lösung:
k
, b<0
mit
1 + ea+bx
P 2 P
P
P
xi · ln( yki − 1) − xi · (xi · ln( yki − 1))
P
P
a =
n x2i − ( xi )2
Logistische Funktion:
b =
n
ŷ =
bekannter Sättigungsgrenze
P
P
P
(xi · ln( yki − 1)) − xi · ln( yki − 1)
P
P
n x2i − ( xi )2
Arbeitstabelle:
xi = Jahr − 1991
Verwenden dabei folgende Zeittransformation:
− 1) xi · ln( 80
− 1)
ln( 80
yi
yi
Jahr
xi
x2i
yi
1992
1
1
3
3,245193
3,245193
1993
2
4
8
2,197225
4,394449
1994
3
9
19
1,166435
3,499305
1995
4
16
33
0,353640
1,414560
1996
5
25
50
-0,510826
-2,554128
1997
6
36
63
-1,309921
-7,859528
1998
7
49
74
-2,512306
-17,586139
28
140
2,629440
-15,446289
P
a =
140 · 2, 629440 − 28 · (−15, 446289)
800, 617683
=
= 4, 084784
2
7 · 140 − 28
196
b =
181, 74834
7 · (−15, 446289) − 28 · 2, 629440
=
−
= −0, 9273
7 · 140 − 282
196
Ergebnis:
ŷ =
80
1 + e4,085−0,927x
Schätzwert für 2000:
ŷ(9) =
80
1 + e4,085−0,927·9
= 78, 887
4
k
k
1 + ea+bx
5