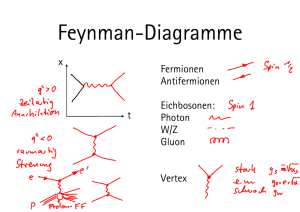
Vorwort - Springer

V
Vorwort
You can’t learn anything without teaching.
J. A. Wheeler
Dieses Lehrbuch ist – wie viele andere auch – aus Vorlesungen entstanden. An
der Technischen Hochschule Aachen habe ich die Kursvorlesung Elementarteilchenphysik I/II sehr oft gehalten. Naturgemäß wuchs der Umfang des sich
daraus entwickelnden Lehrbuchs weit über den Rahmen der Vorlesung hinaus,
obwohl die grundsätzliche Struktur übernommen wurde.
Ein Vorläufer dieses Buches ist mein 1992 erschienenes Lehrbuch ,,Teilchenphysik“, welches eine überraschend freundliche Aufnahme gefunden hat.
Allerdings wurde immer wieder das Fehlen eines Abschnitts über Teilchenbeschleuniger und Detektoren bedauert. Eine Behandlung dieser Themen war
daher für eine eventuelle Neuauflage vorgesehen. In der Zwischenzeit hat sich
aber unser Gebiet so stürmisch entwickelt, daß bei einer Berücksichtigung
der neuen Ergebnisse der Umfang von etwa 270 Seiten auf über 450 Seiten
anstieg. Daraus ist dann ein neuer Text entstanden.
Die Hörer der Vorlesung sind Studenten im 6. und 7. Semester. Ich versuche
daher, ein konsistentes Bild der modernen Teilchenphysik auf der Grundlage
einer soliden Kenntnis der nichtrelativistischen Quantenmechanik sowie der
Atom- und Kernphysik zu vermitteln. Alle anderen benötigten Hilfsmittel, wie
z.B. Dirac-Gleichung und Feynman-Graphen, werden im Buch bereitgestellt.
Insbesondere die Behandlung der Feynman-Graphen ist hierin beispielhaft für
eine moderne Form des Lernens. Es ist manchmal unumgänglich, zunächst
die Anwendung von intuitiv ansprechenden Regeln zu üben und erst in einem
späteren Teil des Studiums deren exakte Begründung zu erlernen. Jeder wendet
heute Computer zur Lösung numerischer oder algebraischer Probleme an,
ohne etwas über Turing-Maschinen oder Digitalelektronik usw. zu wissen.
Die Experimente der Teilchenphysik werden zur Zeit immer mit den Vorhersagen des sog. Standard-Modells verglichen. In diesem Sinne ist auch das
vorliegende Buch eine Abhandlung über das Standard-Modell. Da Physik
keine historische Wissenschaft ist, folge ich in der Entwicklung des Modells
nicht dem historischen Weg. Es erschien mir richtiger, gleich zu Beginn die
qualitativen Grundlagen zu beschreiben und die ausführliche Behandlung den
späteren Abschnitten zu überlassen. Es ist ganz im Sinne dieses unhistorischen Ansatzes, daß z.B. die Gruppe SU3 nicht an Hand der Quark-Arten
sondern über ihre Farben eingeführt wird.
Die Entwicklung des Standard-Modells ist untrennbar mit dem überwältigenden Erfolg der Eichtheorien verbunden, wozu es einige ausgezeichnete
Bücher gibt. Ich habe daher im vorliegenden Buch auf eine Darstellung der
theoretischen Grundlagen verzichtet. Hinzu kommt, daß einige der in diesem
formalen Rahmen erzielten Resultate auch an Hand der weit anschaulicheren
Diskussion des Verhaltens von Wirkungsquerschnitten bei hohen Energien
gewonnen werden können.
VI
Vorwort
Die Erfolge des Standard-Modells beim Berechnen der Reaktionswahrscheinlichkeiten für die verschiedensten Prozesse verstellen manchmal den
Blick darauf, daß sich manche dieser Ergebnisse auch ohne ein spezifisches
Modell erreichen lassen. Daher wurde im zweiten Kapitel des Buches der
Betrachtung der Symmetrieoperationen der Teilchenphysik ein breiter Raum
gewidmet. Besonderer Wert wurde hierbei auf den Helizitätsformalismus,
d.h. auf eine konsistente Beschreibung des Spins, gelegt. Dieser Formalismus ist gerade für den Experimentalphysiker von unschätzbarem Wert, wenn
es z.B. darum geht, aus Winkelverteilungen der Reaktionsprodukte auf den
Spin von Teilchen zu schließen. Vielleicht werden diese Kenntnisse bei der
Entdeckung neuer Teilchen und der Bestimmung ihrer Quantenzahlen an
zukünftigen Beschleunigern wieder besonders wichtig werden.
Der vorliegende Text ist auch aus vielen Diskussionen entstanden, die ich
mit jungen Physikern im Rahmen der Anfertigung ihrer Diplom- und Doktorarbeiten führen konnte. Es wurde deshalb versucht, die meisten der Begriffe
und Formeln, die in der täglichen Arbeit benötigt werden, zu diskutieren. In
einem einführenden Buch ist dies natürlich nur in einem beschränkten Umfang möglich. Nichtsdestoweniger habe ich das Buch in diesem Sinne auch
für mich selbst geschrieben.
Das Studium der Physik ist sicher schwierig. Es ist ganz natürlich, daß ein
Student den Text nicht einfach lesen kann, sondern sich den Inhalt mit Papier
und Bleistift in der Hand erarbeiten muß. Um dem Anfänger zu helfen, beziehen sich die Literaturangaben in den meisten Fällen nicht auf die Originalarbeiten, sondern auf weiterführende Lehrbücher. Inzwischen erlaubt das Internet einen engen Kontakt zwischen Leser und Autor. Auf der web page des Buches (http://mozart.physik.rwth-aachen.de/elmt.html) sind zusätzliche Angaben zu den Lösungen der Übungsaufgaben zu finden. Hier
sollen aber auch eventuelle Fehler oder Unklarheiten korrigiert werden. Damit
dies möglich ist, brauche ich Ihre Mitarbeit.
Aachen, im Juli 2001
Christoph Berger
5
Elektronen und Quarks
Einführung
Inhalt
D
5.1 Elektron-Positron-Annihilation
in Hadronen . . . . . . . . . . . . . . . 297
ieses Kapitel behandelt elektromagnetische Reaktionen von Elektronen und Hadronen, also die Prozesse, die durch den Austausch von
Photonen beschrieben werden können. Das ist v.a. die Elektron-PositronPaarvernichtung in Hadronen bei Schwerpunktsenergien weit unterhalb
der Masse des Z 0 -Bosons. Genausowichtig ist die (inelastische) ElektronProton-Streuung bei Werten von |q 2 |, die klein gegenüber der Masse
der W- und Z-Bosonen sind. Im Quarkmodell werden diese Reaktionen
als elektromagnetische Streuprozesse zwischen Elektronen und Quarks
interpretiert. Sobald Quarks im Spiel sind, kann die elektromagnetische
Wechselwirkung nicht mehr ohne Beachtung der Quantenchromodynamik
behandelt werden. Die QCD kommt auf zwei Weisen ins Spiel: erstens über
störungstheoretisch erfaßbare Korrekturen der elektromagnetischen Querschnitte, zweitens über die Beschreibung der Hadronisierung der Quarks
und Gluonen; letztere ist störungstheoretisch nicht berechenbar.
5.1 Elektron-Positron-Annihilation in Hadronen
5.1.1 Der Wirkungsquerschnitt
Falls freie Quarks beobachtet werden könnten, wäre die Reaktion
e− + e+ → q + q̄
(5.1)
nur eine fast triviale Variante der in Abschn. 3.2.1 behandelten Myon-Paarerzeugung in Elektron-Positron-Stößen mit einem totalen Wirkungsquerschnitt
σ=
f
Q 2f
4πα2
.
s
(5.2)
Die Summe √
läuft hier über alle Quarksorten f , die bei einer Schwerpunktsenergie von s = 2E erzeugt werden können. Die Summation über die drei
Farbfreiheitsgrade ergibt einen Faktor drei, der in (5.2) schon enthalten ist.
Die Reaktion (5.1) kann nicht direkt beobachtet werden, da es keine freien
Quarks gibt. Die Erzeugung von Hadronen in Elektron-Positron-Stößen, also
die Reaktion e− e+ → X, wobei X ein beliebiger hadronischer Endzustand
ist, kann jedoch im Quarkmodell als ein Zwei-Stufen-Prozeß interpretiert
werden. In der ersten Stufe werden Quark-Antiquark-Paare erzeugt, die anschließend hadronisieren. Man könnte nun zunächst vermuten, daß die durch
den Einschluß der Quarks erzwungene Hadronisierung die Amplitude auf
eine solche Weise verändert, daß jede Ähnlichkeit mit dem Wirkungsquerschnitt (5.2) verlorengeht. Das ist aber nicht so, da Paarerzeugung und
Hadronisierung bei zwei ganz verschiedenen Abstandsskalen d stattfinden.
5.2 Die elastische
Elektron-Nukleon-Streuung . . . 309
5.3 Inelastische
Elektron-Nukleon-Streuung . . . 316
5.4 Zwei-Photonen-Physik . . . . . . . 336
297
298
5
Elektronen und Quarks
1 Diese halbklassische Abschätzung wurde
schon in den Übungen zu Abschn. 1.1 benutzt.
Sie vernachlässigt den Spin der Quarks.
Um dieses Argument in voller Schärfe zu sehen, nehmen wir als Beispiel
eine Strahlenergie E von 5 GeV an. Das bei der Annihilation von Elektron
und Positron entstehende Photon hat den Spin 1. Wenn er durch den relativen
Bahndrehimpuls von Quark und Antiquark aufgebaut werden soll, gilt Ed ≈ 1,
so daß die Paarerzeugung bei einem Abstand von d ≈ 1/25 fm passiert.1 Bei
einem solchen Abstand sind die Quarks praktisch frei und können gemäß
der Kinematik freier Teilchen auseinanderlaufen. Das Einschluß-Potential
der QCD verhindert die Separation der Quarks auf Abstände, die wesentlich
größer als 1 fm sind. Im Prinzip müßte jetzt der Querschnitt (5.2) mit der
Wahrscheinlichkeit W f multipliziert werden, einen bestimmten hadronischen
Endzustand zu erreichen. Wenn man aber nicht einen speziellen hadronischen
Endzustand betrachtet,
sondern über alle möglichen Konfigurationen summiert, gilt natürlich
W f = 1, so daß (5.2) die theoretische Vorhersage des
Quarkmodells für die Hadronerzeugung in der Elektron-Positron-Vernichtung
ist. Mit diesem Trick werden die Probleme der Hadronisierung sehr elegant
ausgeschaltet.
Die Skala der Hadronerzeugung ist also durch den Wirkungsquerschnitt zur
Erzeugung von µ− µ+ -Paaren definiert. Man gibt daher i.allg. als Vorhersage
des Quarkmodells das Verhältnis
σ(e− e+ → Hadronen)
R=
Q 2f
(5.3)
=
3
σ(e− e+ → µ− µ+ )
f
an. Das ist eine sehr bemerkenswerte Voraussage, bedeutet sie doch, daß
dieses Verhältnis in Stufen anwächst, z.B. ∆R = 4/3 beim Überschreiten der
charm-Schwelle.
Die Abb. 5.1 zeigt die gute Übereinstimmung des Experiments
√ mit der
Theorie über einen sehr weiten Bereich der Schwerpunktsenergie s. Das Erstaunliche ist, daß schon bei sehr niedrigen Energien oberhalb der Schwelle
für die Erzeugung von ρ, ω, Φ-Mesonen die Hadronproduktion durch das
Quarkmodell weitgehend richtig wiedergegeben wird.
√ Andererseits darf nicht
übersehen werden, daß im Bereich von 5 GeV < s < 8 GeV die Daten deutlich oberhalb der theoretischen Vorhersage liegen. Eine Nachmessung wäre
hier sehr wünschenswert.
Die Formel (5.3) beschreibt die Hadronproduktion über den Mechanismus
der Erzeugung schneller Quarks mit anschließender Hadronisierung. Beim
Überschreiten einer neuen Schwelle ist die Relativbewegung der neuen Quarks
zunächst so langsam, daß gebundene Zustände, die Vektormesonen, erzeugt
werden können. Diese Reaktionen wurden schon in Abschn. 4.6.1 behandelt.
Der Bereich zwischen den Vektormesonen wird häufig als Kontinuum bezeichnet. Es gibt demnach zwei Möglichkeiten, eine weitere Sorte Quarks zu
finden: Beobachtung eines neuartigen Vektormesons oder eine Stufe von R
im Kontinuum.
Eine Schwelle in R muß allerdings nicht unbedingt von einer neuen Quarksorte herrühren. Auch andere neue Teilchen, die in Hadronen übergehen,
erhöhen dieses Verhältnis. Die τ-Leptonen z.B. zerfallen zu ca. 70 % in
Hadronen und tragen daher mit ∆R ≈ 0,9 zur Hadronerzeugung in ElektronPositron-Stößen oberhalb einer Schwerpunktsenergie von etwa 4 GeV bei.
5
5.1 Elektron-Positron-Annihilation in Hadronen
R
J/ψ ψ'
6
udscbt
udscb
4
udsc
2
uds
2
3
4
5
6 7 8 9 10
20
30
40
s/GeV
Beim Erstellen der Abb. 5.1 wurden aber Ereignisse mit Hadronen aus
τ-Zerfällen in der Bestimmung der Raten nicht berücksichtigt. Sie zeigt daher
nur die Produktion von Hadronen über Quarks, ist also sozusagen ,,theoretisch vorbelastet“. Man sieht daran vielleicht am deutlichsten, wie sehr wir
inzwischen von der Richtigkeit des Modells überzeugt sind.
Schlüsselexperiment
Das τ-Lepton wurde 1975 mit dem gleichen Detektor entdeckt, mit
dem schon die ψ-Resonanzen in der e− e+ -Vernichtung gefunden wurden [Per75]. Das Vorgehen der Experimentatoren kann als Musterbeispiel
für viele ähnliche, spätere Experimente auf der Suche nach neuen Teilchen gelten. Die Aufgabe war besonders schwierig, da im Bereich einer
Schwerpunktsenergie von 4 GeV auch die Paarerzeugung von c-Quarks
möglich ist. Die Autoren wählten zunächst Ereignisse mit genau zwei entgegengesetzt geladenen Spuren in einem ansonsten leeren Detektor aus.
Sie benutzten dann zu ihrer Suche nach neuen Leptonen die Signatur
e− + e+ → e± + µ∓ + fehlende Energie .
(5.4)
Auf den ersten Blick verletzen solche Ereignisse die Erhaltung der
Elektronen- und Myonenzahl. Der gewählten Signatur liegt jedoch die
Hypothese zugrunde, daß die in der Reaktion
e− + e+ → τ − + τ +
(5.5)
erzeugten τ-Paare Zerfallskanäle wie das Myon haben, also z.B.
τ + → ν̄τ µ+ νµ oder τ − → ντ e− ν̄e . Die auslaufenden Neutrinos sind demnach für die fehlende Energie im Detektor und für die scheinbare Verletzung
der L e - und L µ -Erhaltung verantwortlich. Es ist klar, daß der in einem
solchen Experiment verwendete Detektor eine sehr gute Erkennung von
Elektronen, Photonen und Myonen über einen großen Bereich des Raumwinkels erlauben muß. Auf diese Weise kann man dann z.B. beweisen,
Abb. 5.1
Die inklusive Hadronerzeugung in der
e− e+ -Annihilation. Die Meßwerte stammen von 14 verschiedenen Experimenten
mit Normierungsfehlern, die bis zu 20 %
betragen können. Die fast waagerechten Linien sind die Vorhersagen gemäß (5.3) nach
Berücksichtigung der QCD-Korrekturen
aus (5.17)
299
300
5
Elektronen und Quarks
daß ein Elektron nicht durch eine Myonspur vorgetäuscht wird, die zufällig
mit einem durch ein Photon ausgelösten elektromagnetischen Schauer zusammenfällt. Die Autoren führten diesen Beweis, indem sie zeigten, daß
der Impuls der Elektronkandidaten aus der Vermessung der Spur mit der
Energie des zugehörigen kalorimetrischen Signals übereinstimmte.
Die Eigenschaften und die Rate der so ausgewählten Ereignisse konnten
mit der Hypothese (5.5) erklärt werden, während keine andere Annahme
auf die Daten paßte. Eine typische Quelle von Untergrund, die studiert
werden muß, sind z.B. Zwei-Photonen-Reaktionen e− e+ → e− e+ µ− µ+ ,
bei denen jeweils ein Elektron und ein Myon, den Detektor entlang der
Strahlröhre verlassen.
Martin L. Perl, der Leiter dieser Analyse, erhielt 1995 den Nobelpreis
für Physik. Zusammen mit ihm wurde Frederick Reines für die Entdeckung
des Elektron-Neutrinos (Beschreibung auf S. 24f.) geehrt.
5.1.2 QCD-Korrekturen
Sobald Quarks im Spiel sind, macht es keinen Sinn, die elektromagnetische
Wechselwirkung von der starken Wechselwirkung getrennt zu behandeln.
In niedrigster Ordnung der Störungstheorie z.B. kann die elektromagnetische Paarerzeugung von Quarks (Abb. 5.2a) durch die Abstrahlung eines
zusätzlichen Gluons modifiziert werden (Abb. 5.2b,c). Die Berechnung des
differentiellen Wirkungsquerschnitts für die Reaktion
e− + e+ → q + q̄ + g
(5.6)
soll jetzt besprochen werden. Ein wichtiges Problem, das die Autoren
der ersten Rechnung [Ruj78] lösen mußten, war die Bestimmung des
Phasenraumintegrals für den Drei-Körper-Endzustand dieser Reaktion, das
im allgemeinsten Fall noch von fünf Variablen abhängt (Abschn. 2.1.2). Wir
werden dies hier nicht nachvollziehen, sondern den teilweise integrierten
Wirkungsquerschnitt auf eine einfachere Art finden.
+
Dazu interpretieren wir die Annihilationsreaktion e− e√
→ q q̄g als
Erzeugung und Zerfall eines virtuellen Photons der Masse s. Der Wirkungsquerschnitt läßt sich in der Gestalt der Breit-Wigner-Formel (2.261)
anschreiben, wobei im kinematischen Vorfaktor MR2 = s gesetzt wird. Die
r
relativistische Breit-Wigner-Funktion f BW
kann als das Betragsquadrat des
Propagators eines instabilen Teilchens aufgefaßt werden. Wir ersetzen sie
daher durch das Betragsquadrat 1/s2 des Photonpropagators und bekommen
12πΓee Γ f
.
(5.7)
s2
In diesem Formalismus wird die Annihilation e− e+ → µ− µ+ durch σ =
12πΓee2 /s2 beschrieben, da Myonen und Elektronen mit der gleichen Stärke
an Photonen koppeln. Der Vergleich mit (5.2) liefert dann das Resultat
√
α s
Γee =
.
(5.8)
3
σ=
5
5.1 Elektron-Positron-Annihilation in Hadronen
Abb. 5.2a–f
Feynman-Diagramme der Elektron-Positron-Annihilation bis zur Ordnung αS der
QCD. (a) Bornsche Näherung, (b), (c) reelle QCD-Korrekturen, (d)–(f) virtuelle
QCD-Korrekturen
g
−
q
e
q
−
e
+
a)
b)
c)
d)
e)
f)
Die Behandlung des Drei-Körper-Zerfalls eines Teilchens in Abschn. 2.1.2
lehrt uns, daß die Energien und relativen Winkel der drei Teilchen im Endzustand vollständig durch die Angabe von zwei Energien definiert sind.
Es ist praktisch, dimensionslose Variablen zu wählen, z.B. x1 = E q /E und
x2 = E q̄ /E. Um den differentiellen Querschnitt
d2 σ
4πα d2 Γ f
(e− e+ → q q̄g) = √
dx1 dx2
s s dx1 dx2
(5.9)
zu erhalten, müssen wir die differentielle Zerfallsbreite dΓ f / dx1 dx2 eines virtuellen Photons in ein Quark-Antiquark-Paar und ein Gluon berechnen. Dieser
Zerfall ist mit dem virtuellen Compton-Effekt (siehe Kasten auf S. 214f.) durch
eine crossing-Relation verwandt, die in Abb. 5.3 erläutert wird. Die Summe
der Amplitudenquadrate für den Zerfall des virtuellen Photons kann also sehr
schnell aus (3.234) gewonnen werden. Die Mandelstam-Variablen s, t, u werden zunächst mit einem Dachsymbol versehen, da es sich um die Berechnung
eines Subprozesses handelt. Wie bei der Comptonstreuung gilt û = (k − p )2
und tˆ = (k − k )2 . Entsprechend der Vorschrift der Abb. 5.3 wird aber ŝ durch
ŝ2 = (k − p̄)2 ersetzt. Außerdem muß beachtet werden, daß die Überkreuzung
301
302
5
Elektronen und Quarks
Abb. 5.3
Der Zusammenhang zwischen dem virtuellen Compton-Effekt und dem Zerfall eines
virtuellen Photons durch Kreuzen einer Fermionlinie. Die Symbole bezeichnen die
Viererimpulse der Teilchen
p'
k'
p'
k
p
k'
p = − p−
k
einer Fermionlinie ein globales Minuszeichen beisteuert. Die Ersetzung der
Elektronen und Photonen im Endzustand durch Quarks der Sorte f und
Gluonen läßt sich durch die Substitution e4 → e2 Q 2f g2 cF bewerkstelligen.
Zusammengefaßt erhalten wir also
û ŝ2 2k2 tˆ
2
2 2 2
.
(5.10)
|T fi | = 8e Q f g cF
+ +
ŝ2 û
ŝ2 û
Den Ausdruck in der Klammer werten wir im e− e+ -Schwerpunktsystem aus.
Dort gilt kµ = (2E, 0, 0, 0) und daher û = k2 (1 − x1 ) bzw. ŝ2 = k2 (1 − x2 ). Mit
tˆ = k2 − û − ŝ2 und k2 = 4E 2 kann der Klammerausdruck als eine Funktion
von x1 und x2 angegeben werden, welche die übersichtliche Form
f(x1 , x2 ) =
x12 + x22
(1 − x1 )(1 − x2 )
(5.11)
annimmt.
Mit den Methoden der Berechnung des Farbfaktors haben wir uns schon in
Abschn. 4.2.1 befaßt. Ihre Anwendung ergibt im Fall der Abstrahlung eines
Gluons von einem Quark einer bestimmten Farbe einen Faktor 4/3, der Beweis
wird als Übungsaufgabe gestellt. Nach Summation über die drei Farben folgt
demnach cF = 4.
Zur Mittelung über die Spins des zerfallenden virtuellen Photons wird die
Summe der quadrierten Amplituden durch drei geteilt. Die Anwendung von
(2.49) führt dann zum Resultat
d2 Γ f
2 √
=
sααS Q 2f f(x1 , x2 ) ,
(5.12)
dx1 dx2
3π
das in (5.9) eingesetzt werden muß. Wenn wir jetzt über alle Quarksorten
summieren und die Abkürzung
4πα2
(5.13)
σ0 =
Q 2f
s
f
benutzen, erhalten wir das Endergebnis
d2 σ
2αS
= σ0
f(x1 , x2 ) .
dx1 dx2
3π
(5.14)
5
5.1 Elektron-Positron-Annihilation in Hadronen
Diese berühmte Formel [Ruj78] beschreibt demnach die Abstrahlung von
Gluonen als Produkt des Querschnitts (5.2) der Elektron-Positron-Paarvernichtung in q q̄-Paare mit einem Faktor, der die Kopplung αS und die
Verteilungsfunktion der Energien enthält. Die gleiche Struktur haben wir
schon bei der Behandlung der Bremsstrahlung (3.275) vorgefunden und es
überrascht nicht, daß auch hier die Energie- und Winkelverteilung der Gluonen sehr ähnlich zu den Verteilungen der Photonen bei der Bremsstrahlung
sind. Die meisten Gluonen haben eine kleine Energie und einen kleinen Winkel relativ zum Quark, von dem sie abgestrahlt werden. Sie machen sich
daher nur in einer Modifikation des totalen Querschnitts (5.2) bemerkbar.
Um diese Modifikation in der Ordnung αS zu bekommen, müssen wir (5.14)
über x1 , x2 in den Grenzen von 0 bis 1 integrieren und sind wieder mit dem
Divergenzproblem konfrontiert.
Die Struktur der Divergenz ist hier noch komplizierter als bei der Bremsstrahlung. Auch hier finden wir die Infrarot-Divergenz, da mit der Definition
x3 = E g /E der Energiesatz die Form
x1 + x2 + x3 = 2
(5.15)
annimmt und daher ein verschwindender Wert von x3 gleichzeitig x1 → 1 und
x2 → 1 erzwingt. Zusätzlich haben wir aber noch die separaten kollinearen
Divergenzen x1 → 1 bzw. x2 → 1, die auftreten, wenn das Gluon parallel zum
Quark oder Antiquark abgestrahlt wird. In der Bremsstrahlung tauchen diese
Divergenzen bei Berücksichtigung der Masse der Elektronen nicht auf.
Auch jetzt lassen sich die Divergenzen durch Hinzunahme der virtuellen Korrekturen der Abb. 5.2 beheben. Genau wie bei der Behandlung der
Bremsstrahlung muß man die Werte aus Abb. 5.2b,c quadrieren und die Interferenz von a) mit d) bis f) der Abb. 5.2 berechnen. In einer durchsichtigen
Schreibweise läßt sich diese Vorgehensweise in die Form
σ ∼ |A|2 + |B + C|2 + 2 Re[A∗ (D + E + F)]
bringen. Das Ergebnis dieser Rechnung lautet
αS (s)
− +
σ(e e → Hadronen) = σ0 1 +
,
π
(5.16)
(5.17)
wobei im Sinne der verbesserten Bornschen Näherung die laufende Kopplungskonstante αS (q 2 ) mit q 2 = s eingesetzt wurde. Bei s = 1000 GeV2 gilt
aber αS ≈ 0,16, die Korrektur aufgrund der starken Wechselwirkung beträgt
daher etwa fünf Prozent. Die Genauigkeit moderner Annihilationsexperimente reicht aus, den Einfluß dieser Korrektur zu sehen. Dies ist in Abb. 5.1
angedeutet, in der die zu hohen Energien abnehmende Kurve mit Hilfe
der Formel (5.17) gewonnen wurde. Die inklusive Hadronerzeugung in der
Elektron-Positron-Paarvernichtung gilt trotz des numerisch kleinen Effektes als attraktiver Weg zur Bestimmung der Kopplungskonstanten αS , da es
hier keine theoretischen Unsicherheiten infolge von Hadronisierungskorrekturen gibt. Nicht zuletzt aus diesem Grunde wurden die störungstheoretischen
Rechnungen zu höheren Ordnungen hin erweitert. Heute ist die Reihe bis zur
303
304
5
Elektronen und Quarks
Ordnung αS3 bekannt. Bei Berücksichtigung von fünf Quarksorten lautet das
Ergebnis
α 2
α 3 αS
S
S
σ(e− e+ → Hadronen) = σ0 1 +
+ 1,409
− 12,805
,
π
π
π
(5.18)
eine wirklich bewundernswerte Leistung [Sur91] der theoretischen Physiker,
wenn man die große Zahl der beitragenden Diagramme bedenkt.
5.1.3 Der Endzustand
Den Übergang von Quarks (und Gluonen) zu Hadronen im Kontinuumsbereich bezeichnen wir häufig als Fragmentierung. Diese Fragmentierung ist
störungstheoretisch nicht berechenbar, da sie bei großen Abständen stattfindet. Der Endzustand der Reaktion (5.1) besteht aber trotzdem nicht in einer
statistischen Gleichverteilung von Hadronen über den Raumwinkel, sondern
zeigt ganz handgreiflich die q q̄-Natur der Ereignisse. Die Hadronen sind
nämlich in sog. Jetsgebündelt, deren Gesamtenergie durch die Energie E q des
Quarks, aus dem sie hervorgehen, festgelegt wird. Jets zeichnen sich dadurch
aus, daß in ihnen alle Hadronen bezüglich der Jetachse einen relativ kleinen Transversalimpuls von pT ≈ 300 MeV haben. Die Longitudinalimpulse
pL skalieren bis auf logarithmische Korrekturen mit der Energie E q der Jets,
werden also durch eine Verteilungsfunktion Dh (z) beschrieben, die nur von
der dimensionslosen Variablen
pL
z=
(5.19)
Eq
abhängt. Die logarithmischen Korrekturen am Skalenverhalten der Longitudinalimpulse sind so zu verstehen, daß ein kleiner Teil der zur Verfügung
stehenden Energie zur Produktion neuer Teilchen verbraucht wird, die Teilchenmultiplizität steigt logarithmisch mit der Energie an. Eine unmittelbare
Konsequenz des Skalenverhaltens besteht darin, daß die Öffnungswinkel der
Jets, die natürlich proportional zu pT / pL sind, bei höheren Energien wie 1/E
schrumpfen.
Die Reaktion (5.1) sollte infolge dieser qualitativen Überlegungen zu sog.
Zwei-Jet-Ereignissen führen, bei denen E q mit der Strahlenergie E identisch
wird und die Jetachse der Richtung der Quarks entspricht. Ein Beispiel eines
solchen Zwei-Jet-Ereignisses in der e− e+ -Annihilation zeigt Abb. 5.4. Aufgetragen sind die Spuren der Teilchen in einer Ansicht senkrecht zur Achse
der einfallenden Elektronen bzw. Positronen.
Experimentell läßt sich die Jetachse für Ereignisse der Reaktion (5.1) mit
Hilfe der thrust-Variablen T finden,
| pi n|
T = max i
.
(5.20)
i | pi |
Summiert wird über alle Hadronen eines Ereignisses. Man sucht hiermit also
eine Richtung n, bezüglich der die Summe der Longitudinalimpulse der Hadronen maximal wird. Wenn die Gleichsetzung der Jets mit den Quarks richtig
ist, muß die Winkelverteilung der T -Achse in der Annihilation dem Gesetz
5
5.1 Elektron-Positron-Annihilation in Hadronen
TASSO
1
Abb. 5.4
Ein Zwei-Jet-Ereignis der e− e+ -Vernichtung
im TASSO-Detektor am Speicherring PETRA des DESY. Gezeigt ist die Projektion
der Spuren auf eine Ebene, die senkrecht
zu den einfallenden Strahlen durch den
Wechselwirkungspunkt geht
14,9
11
10,5
2
3
13,1
10 12,8
13,7
6
14,2
8
y
5
10,4
x
13,3
(3.147) folgen. Dies wurde in der Tat gefunden und bedeutete eine wesentliche
Unterstützung für die Beschreibung der Elektron-Positron-Annihilation in
Hadronen durch das Quarkmodell.
Die thrust-Variable T ist auch sehr gut zur Charakterisierung der Ereignistopologie geeignet. Ihr Wert beträgt naturgemäß 1 für Ereignisse mit zwei
unendlich gut kollimierten Jets und 0,5, falls die auslaufenden Hadronen eine
isotrope Winkelverteilung haben. Es ist nun besonders reizvoll, die Mittelwerte T aus vielen vermessenen hadronischen Reaktionen im Detektor mit
den theoretischen Vorhersagen auf dem sog. Parton-Niveau zu vergleichen,
wobei nun die Summation in (5.20) über die Quarks und Gluonen des Endzustandes läuft.2 Bei der Betrachtung der Partonen gilt T = 1 im Grenzfall
reiner q q̄ Ereignisse, während durch die Abstrahlung von Gluonen T < 1
wird.
Die Observable T hängt im Zähler und im Nenner nur linear von den
Impulsen der betrachteten Teilchen ab. Sie gehört zu den theoretisch besonders
interessanten Variablen, die als ,,infrarot und kollinear“ stabil gelten, da sich
ihr Wert bei Abstrahlung eines weichen oder kollinearen Gluons von einem
Quark nicht ändert. Sie ist daher unempfindlich gegen die unvermeidlich
auftretenden Divergenzen in den störungstheoretischen Rechnungen.
In führender Ordnung der QCD kann T mit Hilfe von (5.14) berechnet
werden [Ruj78], das Ergebnis lautet
1 − T = 0,335αS .
(5.21)
2 Das
Wort Parton wird oft als Sammelbegriff
für Quarks und Gluonen verwendet.
305
306
5
Elektronen und Quarks
Wenn für αS jetzt wieder die laufende Kopplungskonstante eingesetzt wird,
stellt (5.21) eine relativ einfach zu überprüfende Vorhersage der QCD dar,
mit der v.a. das Konzept der asymptotischen Freiheit getestet werden kann:
1 − T muß in einer wohldefinierten Weise für hohe Werte von s gegen Null
streben.
Natürlich darf (5.21) nicht direkt mit dem hadronischen Wert verglichen
werden. Aufgrund der Fragmentierungseffekte wird auch ein Zwei-JetEreignis T < 1 haben. Auf die numerischen Verfahren zur Berechnung der
Hadronisierung gehen wir am Schluß dieses Abschnitts nochmal ein. Da die
einzelnen Hadronen in den Jets bevorzugt die Richtung des ursprünglichen
Quarks beibehalten und häufig nur kleine Bruchteile des Quarkimpulses
übernehmen, erwarten wir, daß T ebenfalls relativ unempfindlich gegen Details des Fragmentierungsprozesses ist. Aufgrund sehr allgemeiner
Überlegungen [Sti96] wurde gezeigt, daß die Korrekturen vom Hadron-Niveau auf das Parton-Niveau umgekehrt proportional zur Schwerpunktsenergie
0,20
1–T
JADE
0,18
Mark J
TASSO
DELCO
Mark II
AMY
DELPHI
L3
ALEPH
OPAL
SLD
0,16
0,14
0,12
0,10
0,08
0,06
0,04
Abb. 5.5
Der Mittelwert von 1 − T in der e− e+ Vernichtung in Hadronen. Es sind Daten verschiedener Experimente zusammengefaßt. Die gestrichelte Kurve gibt eine
perturbative QCD-Rechnung höherer Ordnung wieder, die durchgezogene Kurve
berücksichtigt zusätzlich die Hadronisierungskorrekturen nach [Sti96]
0,02
0
0
20
40
60
80
100
120
140
160
180
s/GeV
5
5.1 Elektron-Positron-Annihilation in Hadronen
abnehmen, so daß
λ
1 − T Hadronen = 0,335αS + √
s
(5.22)
mit λ ≈ 1 GeV angesetzt werden kann.
Das Verhalten der thrust-Observablen und anderer sog. event shapeVariablen wurde ausführlich an den e− e+ -Speicherringen untersucht. Von
diesen Experimenten stammen grundlegende Tests der asymptotischen Freiheit und präzise Messungen der starken Kopplungskonstanten. Für genaue
Analysen reicht (5.21) zum Vergleich mit der Theorie nicht aus, sondern
es werden auch zu dieser Formel die Beiträge höherer Ordnung benötigt.
Ebenso ist die Behandlung der Fragmentierungskorrekturen in keiner Weise
einfach. In Abb. 5.5 ist ein neueres Ergebnis einer zusammenfassenden Studie wiedergegeben, in der der Leser die erreichte Präzision und die gute
Übereinstimmung von Theorie und Experiment bewundern kann.
In einem kleinen Bruchteil aller Fälle führt die Abstrahlung von Gluonen zu spektakulären Drei-Jet-Ereignissen (Abb. 5.6). Diese wurden am
Elektron-Positron-Speicherring PETRA des DESY entdeckt. Die kinematischen Eigenschaften der Drei-Jet-Ereignisse entsprechen den theoretischen
Vorhersagen. Die Energien der beiden energiereichsten Jets werden mit E q
und E q̄ identifiziert, und ihre Verteilung wird mit (5.14) verglichen. Die hierbei gefundene quantitative Übereinstimmung manifestiert eine Art objektiver
Evidenz für Gluonen, die natürlich als farbige Feldquanten ebenfalls dem
e+e–
PLUTO
3
qqg
6
11
4
5
6
12
5
7
8
9
1
2
13
12
4
3
8
2
13
9
11 1
1
Abb. 5.6
Ein typisches Drei-Jet-Ereignis im PLUTODetektor, wie es kurz nach Beginn der Experimente am Speicherring PETRA gefunden
wurde
307
308
5
Elektronen und Quarks
Einschluß (confinement) unterliegen und daher nicht als freie Teilchen im
Detektor auftreten.
Da ein Ereignis mit einem zusätzlichen weichen oder kollinearen Gluon
sich nicht von einem q q̄-Ereignis unterscheiden läßt, muß (wie bei der Behandlung der Bremsstrahlung auf S. 224) ein Auflösungskriterium eingeführt
werden. Dieses Argument gilt auch für die Hadronen des Detektors. Die Analyse von Ereignissen mit mehr als zwei Jets macht also die Entwicklung
allgemeiner Algorithmen zur Rekonstruktion der Jets aus den Impulsen der
Reaktionsprodukte nötig.
Weit verbreitet ist ein Verfahren [Bar86b], welches zunächst die invarianten
Massen aller Paare von Teilchen (oder Partonen) eines Ereignisses nach der
Vorschrift
Mkl2 = 2E k El (1 − cos Θkl )
(5.23)
berechnet, in der Θkl den Winkel zwischen den beiden Teilchen mit den
Energien E k und El kennzeichnet. Die Teilchen i und j mit der kleinsten
µ
µ
Paarmasse werden durch ein Pseudoteilchen mit dem Viererimpuls ( pi + p j )
ersetzt, falls das skalierte Massenquadrat
yij =
3 Als
,,Monte-Carlo“-Methode wird das Nachbilden zufälliger Prozesse auf einem Computer
bezeichnet. Der Name erinnert daran, daß die
Zahlenfolge im Roulette ebenfalls zufällig ist.
Mij2
(5.24)
s
unterhalb eines Schnittwertes ycut liegt, der das Auflösungskriterium darstellt. Der Algorithmus wird nun solange wiederholt, bis alle möglichen
Paare eine invariante Masse ≥ ycut s haben. Diese Kombinationen von Teilchen
und Pseudoteilchen sind die gesuchten Jets. Mit Hilfe solcher Methoden ist
die Erzeugung von drei und mehr Jets in der Elektron-Positron-Annihilation
ausführlich untersucht worden.
Der Übergang von den Quarks und Gluonen zu den Hadronen (die sog.
Fragmentierung) findet bei Abständen der Partonen von 1–3 fm, also bei einer
Zeitskala von 10−23 s statt. Bei diesen Abständen kann die Störungstheorie
nicht mehr angewendet werden. Ein quantitatives Verständnis dieser Prozesse ist jedoch unabdingbar, da alle Untersuchungen eines bestimmten
Endzustandes beim Vergleich mit der Theorie versuchen müssen, von den
hadronisch ermittelten Observablen auf die partonischen Observablen zu
schließen. Zum Abschluß der Diskussion des hadronischen Endzustandes
in der Elektron-Positron-Paarvernichtung soll daher jetzt noch die numerische Behandlung der Fragmentierung mit Hilfe von QCD-Modellen diskutiert
werden.
In Abschn. 4.2.1 haben wir den Einschluß der Quarks im Saitenmodell
behandelt. Die Fragmentierung entspricht dem Zerreißen des Bündels der
Farbfeldlinien zwischen den Quarks. Die in der Gluonfeld-Saite gespeicherte Energie ist im betrachteten Fall so groß, daß sie die Bildung vieler
q q̄-Paare erlaubt. Diesen Vorgang kann man mittels einer ,,Monte-Carlo“Rechnung rekonstruieren.3 Das string-Modell der Hadronisierung wurde v.a.
an der Universität Lund entwickelt und steht heute in Form des ProgrammPakets JETSET [Sjo82] an allen Forschungszentren zur Verfügung. Für
einen q q̄-Zustand liefert es sehr ähnliche Resultate wie das zuvor von Field
5
5.2 Die elastische Elektron-Nukleon-Streuung
und Feynman [Fie78] entwickelte Modell der unabhängigen Fragmentierung
(independent fragmentation). Letzteres hat für uns den Vorteil, daß seine
Grundzüge sich leichter beschreiben lassen.
Dazu nehmen wir an (siehe Abb. 4.8), daß in dem von den auseinanderlaufenden Quarks produzierten Farbfeld zunächst ein Paar q1 q̄1 produziert wird.
Das nach rechts laufende ursprüngliche Quark q mit dem Impuls | pq | formt
mit dem Quark q̄1 ein Meson (q q̄1 ). Der Longitudinalimpuls dieses Mesons,
also die Impulskomponente in Richtung pq , sei z 1 | pq |, das übrigbleibende
Quark q1 hat dann den Longitudinalimpuls p1,L = (1 − z 1 )| pq |. Nun wird ein
Paar q2 q̄2 erzeugt, q̄2 bildet mit q1 ein Meson mit dem Longitudinalimpuls
z 2 | p1 |, und so geht es immer weiter, bis der gesamte Impuls aufgebraucht
ist. Für die Monte-Carlo-Rechnung muß man also nur eine universale Verteilungsfunktion f(z i ) bestimmen, die die Aufteilung der Longitudinalimpulse
in den oben besprochenen Prozessen festlegt. Die Verteilung der Zufallszahlen z 1 , z 2 , ... wird entsprechend dieser Funktion erzeugt. Es ist klar, daß ein
solches Verfahren eine Verteilungsfunktion Dh der Longitudinalimpulse der
Hadronen erzeugt, die nur von der in Formel (5.19) definierten Variablen z
abhängt und damit die weiter oben geforderte Qualität erfüllt. Die Hadronen
bilden also Jets. Zusätzlich simuliert man im Rechenprogramm auch noch den
Transversalimpuls der Mesonen (bezüglich der Richtung pq ) mit einem Mittelwert von etwa 300 MeV, die flavor-Quantenzahlen der Quarks, die Spins
der Mesonen usw.
Es läßt sich denken, daß moderne Hadronisierungsprogramme technisch
sehr kompliziert sind, obwohl sie auf relativ einfachen Prinzipien beruhen. Die
Entwicklung dieser Verfahren ging Hand in Hand mit der Entstehung eines
neuen Zweiges der Physik, der sog. computational physics, bei der nur noch
die Grundannahmen analytisch formuliert werden, während die quantitative
Lösung einer bestimmten Fragestellung ausschließlich numerisch bestimmt
wird.
Übungen
5.1
5.2
5.3
Berechnen Sie den Farbfaktor, der für Quarks einer bestimmten Farbe
im Prozeß q → q + g anzuwenden ist.
Zeigen Sie, daß für einen Endzustand q q̄g aus drei masselosen
Partonen der thrust durch T = max (x1 , x2 , x3 ) gegeben ist.
Berechnen Sie den Mittelwert von T für eine isotrope Verteilung der
auslaufenden Teilchen.
5.2 Die elastische Elektron-Nukleon-Streuung
Bei der Behandlung der QED haben wir die enge Verwandtschaft der ElektronPositron-Paarvernichtung in Myonen und der Elektron-Myon-Streuung
studiert. Ein Übergang von der e− e+ -Annihilation in Quark-Antiquark-Paare
zur Elektron-Quark-Streuung ist aber zunächst nur auf dem Papier möglich,
309
310
5
Elektronen und Quarks
da es offensichtlich keine freien Quarks gibt. Um besser zu verstehen, welche
Revolution des physikalischen Denkens die Interpretation der inelastischen
Elektron-Proton-Streuung im Sinne des Quarkmodells bedeutete, betrachten
wir erst einmal die elastische Streuung
e+ p → e+ p ,
(5.25)
auf die sich auch über viele Jahre hinweg die Anstrengungen der
Experimentalphysiker konzentrierten.
5.2.1 Der Wirkungsquerschnitt
Für die nun folgende Diskussion der elastischen Elektron-Nukleon-Streuung
ist es nützlich, die Formeln in einem System anzugeben, in dem das Zielteilchen (target) ruht. Alle Experimente wurden in einer solchen Anordnung
durchgeführt.
Wir gehen zurück zur elastischen eµ-Streuung, d.h. zur Streuung an einem
punktförmigen Teilchen der Masse M. In einem System mit ruhendem target bekommt die in Abschn. 3.2.2 eingeführte Variable y eine anschauliche
Bedeutung. Mit
E − E
(5.26)
E
wird sie zum relativen Energieverlust des gestreuten Elektrons, wie schon
bei der Behandlung der Ionisation und Anregung auf S. 204f. ausgeführt
wurde. Die Variable t = q 2 hat in diesem System bei Vernachlässigung der
Elektronenmasse m eine ähnlich einfache Form wie im Schwerpunktsystem
y=
t = −2E E (1 − cos Θ) = −4E E sin2 (Θ/2) ,
(5.27)
man muß aber beachten, daß die Energie E des auslaufenden Elektrons
eine Funktion des Streuwinkels Θ im Laborsystem ist. Die Formel (2.188)
vereinfacht sich hier zu
E
E =
.
(5.28)
1 + (2E/M) sin2 (Θ/2)
Mit m = 0 nimmt (3.189) die Gestalt
4πα2
s
y2
dσ
=
1
−
y
+
dq 2
q4
s0
2
(5.29)
an. Hierin ist s = 2E M + M 2 und s0 = 2E M. Wie schon bei der Herleitung der
QED-Formel in Abschn. 3.2.2 betont wurde, ist y in der elastischen Streuung
keine unabhängige Variable. Die Darstellung (5.29) eignet sich aber besonders
gut zur Vorbereitung der Behandlung der inelastischen Streuung. Zunächst
bringen wir jedoch unter Beachtung von
dt
E2
=
dΩ
π
(5.30)
(5.29) in eine Form, die von der Invarianten q 2 und den Variablen des Laborsystems abhängt. Dazu klammern wir – der Tradition folgend – einen Faktor
5
5.2 Die elastische Elektron-Nukleon-Streuung
(1 − y) aus und gewinnen nach einigen weiteren Umformungen
dσ e p
4α2 E 2
1
q2
2
2
=
cos (Θ/2) −
sin (Θ/2) .
dΩ
q 4 1 + (2E/M) sin2 (Θ/2)
2M 2
(5.31)
Hierin haben wir M mit der Masse des Protons gleichgesetzt und somit eine
Formel für die Streuung relativistischer Elektronen an einem ,,Dirac-Proton“,
d.h. einem Spin 1/2-Teilchen mit der Masse eines Protons und dem magnetischen Moment von genau einem Kernmagneton, abgeleitet. Die Darstellung
ist sicherlich nicht ganz konsequent, da auf der rechten Seite neben den
unabhängigen Variablen E und Θ auch die noch von E abhängende Invariante q 2 auftaucht. Es kommt uns aber auch darauf an, dem Leser zu helfen,
vielbenutzte Gleichungen der Lehrbücher (z.B. Formel (7.46) des Buches von
Bjorken und Drell [Bjo66]) wiederzuerkennen.
In der Literatur kann man noch manch andere Darstellung des Wirkungsquerschnitts der elastischen Elektronenstreuung finden. Es sind Variationen
des gleichen Themas. Eine sinnvolle Umformung von (5.31) besteht z.B.
darin, den Faktor cos2 (Θ/2) auszuklammern,
4α2 E 2 cos2 (Θ/2)
1
q2
dσ e p
2
tan (Θ/2) ,
=
1−
dΩ
q4
1+(2E/M) sin2 (Θ/2)
2M 2
(5.32)
weil dann der erste Faktor dem Wirkungsquerschnitt für die Streuung eines
relativistischen Elektrons im Coulomb-Potential entspricht, wie man durch
den Grenzübergang M → ∞ sieht. Die sog. Mottsche Streuformel
dσ
α2
= 2 2 4
[1 − β 2 sin2 (Θ/2)]
dΩ
4 p β sin (Θ/2)
(5.33)
behandelt dieses Problem für beliebige Elektronengeschwindigkeiten β, also
ohne Vernachlässigung der Elektronenmasse.4 Für β → 1 entspricht sie dem
ersten Faktor in (5.32), wenn berücksichtigt wird, daß bei der Potentialstreuung E = E gilt. Der Term cos2 (Θ/2) bringt wieder die Drehimpulserhaltung
zum Ausdruck. Bei einem Streuwinkel von 180◦ führt die Helizitätserhaltung
am Vertex (Abb. 5.7) zu |∆Jz | = 1, daher muß der Wirkungsquerschnitt für
diesen Streuwinkel verschwinden. Es ist auch anschaulich klar, daß dieser
Spinterm nur bei hohen Geschwindigkeiten relevant wird. Im Ruhesystem
des Elektrons erscheint das Streuzentrum nämlich als sich bewegende Ladung. Neben dem elektrischen Feld tritt daher auch ein Magnetfeldanteil
proportional zu β auf. Dieses Magnetfeld koppelt an den Spin des Elektrons.
Im Umkehrschluß wird damit auch einsichtig, daß Spineffekte für β → 0
verschwinden. Die Mottsche Streuformel geht in
dσ
α2 m 2
= 4 4
,
dΩ
4 p sin (Θ/2)
(5.34)
über, dem Rutherfordschen Wirkungsquerschnitt für die Streuung eines spinlosen nichtrelativistischen Teilchens der Masse m im Coulomb-Potential.
Abb. 5.7
Erläuterung der Helizitätserhaltung bei
der Rückwärtsstreuung von Elektronen im
Coulomb-Potential
4 Diese Streuformel wird in dem Buch von Mott
und Massey [Mot65] ausführlich diskutiert.
311
312
5
Elektronen und Quarks
Die berühmte Winkelabhängigkeit wurde von Rutherford durch Betrachtung der Bahnen geladener Teilchen im Coulomb-Feld ohne Verwendung
der Quantenmechanik gefunden.5 In unserer Interpretation kommt sie durch
den Photonpropagator 1/q 2 zustande, der als Faktor (1/q 2 )2 im Wirkungsquerschnitt aller elektromagnetischen Streuprozesse von den niedrigsten bis
zu den höchsten Energien auftritt.
5.2.2 Experimente zur elastischen Elektronenstreuung
Zunächst werfen wir einen Blick auf die Streuung im Coulomb-Potential.
Sie läßt sich experimentell durch Streuung niederenergetischer (E ≈ 2 MeV)
Elektronen an schweren Kernen studieren. Hierzu gibt es ausgedehnte
Untersuchungen der Elektronenstreuung an dünnen Metallfolien. Die genauesten Messungen zeigten, daß alle Abweichungen von der Mott-Formel
auf Beiträge höherer Ordnung, wie die in Abschn. 3.3.2 diskutierten
Strahlungskorrekturen, zurückgeführt werden können [Ber70].
Bei der Diskussion der Experimente zur Elektron-Positron-Annihilation
im letzten Abschnitt haben wir gesehen, daß Elektronen und Myonen sich
wie punktförmige Teilchen verhalten. Eine Überprüfung der QED-Resultate
im raumartigen Bereich, also durch Elektron-Myon-Streuung, ist leider nicht
möglich, da sich Myonen noch nicht in genügender Anzahl herstellen lassen.
Das einzige geladene Spin 1/2-Teilchen, das man als Target für Streuversuche benutzen kann, ist das Proton. Da es aber ein anomales magnetisches
Moment von 2,79 Kernmagnetonen hat, erwarten wir von vornherein, daß
(5.32) modifiziert werden muß. Man könnte nun versuchen, eine zu (5.32)
analoge Formel für die Streuung an einem punktförmigen Teilchen mit
anomalem magnetischen Moment abzuleiten. Weil das Proton aber einen
Radius von etwa 1 fm hat, erwarten wir zusätzliche Abweichungen von
(5.32) schon bei |q 2 | ≈ 0,04 GeV2 , typisch also bei Streuwinkeln von 10◦
für Elektronenstrahlen der Energie 1 GeV.
Den Einfluß der endlichen Ausdehnung des Protons parametrisiert man
durch Einführung zweier Formfaktoren, G E und G M , dem elektrischen
und magnetischen Formfaktor des Protons. Beide hängen von |q 2 | ab.
Solange man den Energieübertrag auf das Proton vernachlässigen kann,
gilt aber auch |q 2 | = q 2 , und der elektrische Formfaktor G E läßt sich als
Fourier-Transformierte der Ladungsverteilung ρ(r)
2
G E (q ) = ρ(r)ei qr d3 r
(5.35)
5 E. Rutherford (1871–1937) entdeckte auf
diese Weise den Atomkern.
6 Die
Radien der Kerne wurden durch die
Messung des elektrischen Formfaktors bestimmt. Das Verfahren wird daher ausführlich
in den Lehrbüchern der Kernphysik behandelt [Bet01, May94].
interpretieren. Ebenso beschreibt G M die Verteilung des magnetischen Momentes. Eine genauere Diskussion dieser Zusammenhänge führt uns zu weit
von unserem eigentlichen Thema, der Wechselwirkung von Leptonen und
Quarks, weg.6 Im Buch von Bjorken und Drell [Bjo66] findet man eine
ausführliche Herleitung der Rosenbluth-Formel
2
dσ
4α2 E 2 cos2 (Θ/2)
G E + τG 2M
2
2
= 4
+
2τG
tan
(Θ/2)
,
M
dΩ
q [1 + (2E/M) sin2 (Θ/2)]
1+τ
(5.36)
5
5.2 Die elastische Elektron-Nukleon-Streuung
die für die Elektronenstreuung an ruhenden Protonen und Neutronen gültig ist.
Das Symbol τ ist eine Abkürzung für |q 2 |/4M 2 , wobei M die Nukleonenmasse
bedeutet.
Für Protonen lauten die Randbedingungen
p
G E (0) = 1
p
G M (0) = 2,79
(5.37)
G nM (0) = −1,91 ,
(5.38)
und für Neutronen
G nE (0) = 0
p,n
d.h. G M (0) sind die magnetischen Momente der Nukleonen in Einheiten
eines Kernmagnetons. Mit G E = G M = 1 für alle Werte von |q 2 | erhält man
(5.32) zurück, wie es auch sein muß.
Die Rosenbluth-Formel enthält die Aussage, daß man bei festem |q 2 |
durch Variation des Streuwinkels die beiden Formfaktoren G E und G M
gemeinsam bestimmen kann. Eine Änderung des Winkels bei festem |q 2 | bedeutet natürlich, daß die Einfallsenergie E der Elektronen an die geänderten
kinematischen Bedingungen angepaßt werden muß. Die so gemessenen Wirkungsquerschnitte teilt man durch den ersten Faktor von (5.36) und trägt
dann das Ergebnis gegen tan2 (Θ/2) auf. Die damit erhaltenen Werte sollten auf der ,,Rosenbluth-Geraden“ liegen, deren Achsenabschnitt durch
(G 2E + τG 2M )/(1 + τ) und deren Steigung durch 2τG 2M gegeben ist. Messungen der Formfaktoren der Nukleonen wurden über einen großen Wertebereich
von |q 2 | durchgeführt. Aus der Normierung der Formfaktoren und aus den in
der Rosenbluth-Formel auftretenden Vorfaktoren ist zu entnehmen, daß schon
für relativ kleine |q 2 |-Werte von etwa 2 GeV2 der Wirkungsquerschnitt durch
G M dominiert ist. Die Meßwerte des elektrischen Formfaktors sind daher i.a.
mit einem größeren Fehler behaftet.
Das experimentelle Resultat kann sehr einfach zusammengefaßt werden.
p
p
Sowohl der Verlauf von G E als auch von G M /µ p läßt sich durch die sog.
Dipolformel
p
p
GE =
GM
1
=
µp
(1 + |q 2 |/a)2
(5.39)
beschreiben, worin der Parameter a empirisch zu a = 0,71 GeV2 bestimmt
wurde. Das Merkwürdige dabei ist, daß dieses Resultat schon von Hofstadter [Hof56] bei der Untersuchung der Ladungsverteilung des Protons bei
sehr kleinen Impulsüberträgen gefunden wurde. Auch der magnetische Formfaktor des Neutrons folgt diesem universellen Verlauf, während G nE (|q 2 |) auch
für große |q 2 | nur wenig von 0 abweicht.
Für hohe Impulsüberträge bedeutet (5.39) auf jeden Fall einen starken Abfall des Wirkungsquerschnitts, σ ∼ 1/q 12 verglichen mit 1/q 4 für
ein punktförmiges Teilchen. Dies ist ein wirklich dramatischer Effekt, und
mit diesem Hintergrund muß man die in Abschn. 5.3 zu besprechenden
Ergebnisse der inelastischen Elektron-Nukleon-Streuung sehen. Das Potenzgesetz 1/q 4 des Formfaktors läßt sich wenigstens qualitativ im Rahmen
der QCD deuten (Abb. 5.8). Wenn die Streuung des Elektrons an einem
p
e−
e−
p
Abb. 5.8
Die elastische Elektron-Nukleon-Streuung
(e p) in der QCD. Hier müssen sich die
Quarks nach der Streuung wieder zu einem
Nukleon arrangieren
313
314
5
Elektronen und Quarks
dσ dσ
1,1 dΩ dΩ
Dipol
1,0
Bonn
Desy
SLAC
0,9
10
20
30
40
50
|q2 |/fm–2
Abb. 5.9
Das Verhältnis des Wirkungsquerschnitts
der elastischen Elektron-Proton-Streuung
zu einer Vorhersage, die aus der Dipolformel
für die Formfaktoren gewonnen wurde
einzelnen Quark stattfindet, müssen die beiden anderen Quarks wieder in
die ursprüngliche Konfiguration gedrängt werden, damit das Proton zusammenhält. Dies geschieht durch Austausch von Gluonen. Die dabei auftretenden
Gluon-Propagatoren 1/q12 und 1/q22 skalieren mit |q 2 |, und daher wird die
Streuamplitude mit einem Faktor 1/q 4 multipliziert.
Das in (5.39) beschriebene Gesetz gibt die experimentellen Resultate mit
einer Genauigkeit von etwa 10 % wieder. In sehr sorgfältigen Untersuchungen wurden Abweichungen von der Dipolformel im Verlauf des elektrischen
und magnetischen Formfaktors festgestellt (Abb. 5.9). Diese Details und der
in (5.39) auftretende Wert der Konstanten a sind bis heute unverstanden.
Gemessen an dem großen experimentellen Aufwand erscheint das Ergebnis
etwas dürftig. Der Vergleich mit den völlig neuartigen Phänomenen, die beim
Übergang zur inelastischen Elektronenstreuung gefunden wurden, zeigt uns,
wie wichtig es in der Teilchenphysik ist, zunächst einmal die groben Effekte
zu entdecken und zu verstehen.
Vertiefung
Das Resultat (5.39) kann für kleine q 2 -Werte anschaulich interpretiert
werden. Dazu wird zunächst (5.35) weiter ausgewertet. Die z-Achse
des Koordinatensystems der Integration legen wir in die Richtung des
q-Vektors. Die Integration über θ und φ ergibt
sin |q|r 2
G E (q 2 ) = 4π ρ(r)
r dr .
(5.40)
|q|r
Für kleine Werte von q 2 wird nun die Sinusfunktion in eine Reihe entwickelt. Unter Beachtung der Normierung der Ladungsverteilung und der
Definition des Mittelwertes r 2 erhalten wir
|q 2 |r 2 .
(5.41)
6
Bei den kleinen Impulsüberträgen, wie sie in den Experimenten von
Hofstadter vorlagen, gilt |q 2 | = q 2 und das Ergebnis (5.39) wird durch
G E (q 2 ) ≈ 1 − 2|q 2 |/0,71 angenähert. In einem Modell des Protons als einer
homogen geladenen Kugel mit dem Radius R berechnet man r 2 = 3R2 /5,
woraus R = 1,05 fm folgt.
G E (q 2 ) ≈ 1 −
5.2.3 Das eπ-System
Die Feynman-Regeln des Abschn. 3.1.3 behandeln nur die Kopplung von
Fermionen an Photonen. Dies ist u.a. dadurch gerechtfertigt, daß die elementaren Bausteine der Materie eben Fermionen sind. Es ist trotzdem reizvoll,
die elektromagnetische Wechselwirkung von skalaren Teilchen zu untersuchen. Als Beispiel diskutieren wir das Elektron-Pion-System, obwohl es sich
bei den Pionen natürlich nicht um elementare punktförmige Konstituenten der
Materie handelt.
5
5.2 Die elastische Elektron-Nukleon-Streuung
Ein- und auslaufende Spin 0-Teilchen werden in den Feynman-Graphen
einfach durch einen Faktor 1 beschrieben, während jedem Vertex ein Faktor
−ieQ( pµ + pµ )
(5.42)
zugeordnet wird (Abb. 5.10). Die Amplitude für die Paarerzeugung
e− + e+ → π − + π +
(5.43)
lautet demnach (mit den in Abb. 5.11a angegebenen Bezeichnungen der
Impulse)
T fi = −e2 v̄(k)γ µ u( p)
1 ( p − kµ ) .
q2 µ
p'
_ i eQ ( pµ + p' µ )
p
Abb. 5.10
Die elektromagnetische Kopplung an skalare Teilchen
(5.44)
Die Auswertung im Schwerpunktsystem der Reaktion ergibt z.B. für linkshändige Elektronen und rechtshändige Positronen unter Benutzung der Resultate
des Abschn. 3.1.3
T fi = −e2 sin Θ ,
(5.45)
wobei Θ der Winkel zwischen dem einlaufenden Elektron und dem auslau1
fenden π + ist. Die Winkelverteilung ist also proportional zu d1,0
, wie es durch
die Bilanz der Spins und Helizitäten gefordert wird. Ausgedrückt durch die
Mandelstam-Variablen lautet die Streuamplitude
2 tu
.
(5.46)
T fi = −2e
s2
Das (im Betrag) gleiche Ergebnis wird für die Annihilation rechtshändiger
Elektronen und linkshändiger Positronen erhalten, und es ist eine sehr einfache
Aufgabe, aus diesen Amplituden nach den üblichen Verfahren
dσ − +
α2 2
(e e → π − π + ) =
sin Θ
dΩ
8s
p'
(5.47)
k'
π+
π−
e−
e
−
e
p
π
+
k
a)
b)
Abb. 5.11a,b
(a) Die e− e+ -Annihilation in Pionen, (b) die
Elektron-Pion-Streuung in niedrigster Ordnung der QED
315
316
5
Elektronen und Quarks
als den spingemittelten Wirkungsquerschnitt im Schwerpunktsystem abzuleiten.
Der Wirkungsquerschnitt der Streureaktion eπ → eπ kann wieder durch
die Substitution s ↔ t im Quadrat der Amplitude (5.46) berechnet werden
und lautet in invarianter Form
dσ
4πα2
(eπ
→
eπ)
=
(1 − y) .
(5.48)
dq 2
q4
Experimentell sind die Abweichungen von diesen Vorhersagen aufgrund
der hadronischen Natur der Pionen am interessantesten. Auch diese werden
durch Formfaktoren beschrieben, mit denen die Streuamplitude multipliziert
wird. Da die π-Mesonen Spin 0-Teilchen sind, gibt es nur einen Formfaktor,
der für den zeitartigen Prozeß mit Fπ (s) und für den raumartigen Prozeß mit
Fπ (q 2 ) bezeichnet wird.
Qualitativ ist klar, daß im Bereich von s ≈ m 2ρ die Größe |Fπ (s)|2 die
Gestalt einer Breit-Wigner-Resonanzkurve annimmt. Wenn andererseits die
Elektron-Pion-Streuung durch ein QCD-Bild analog zur Abb. 5.8 beschrieben
wird, erwartet man
1
Fπ (q 2 ) ∼ 2 ,
(5.49)
|q |
da nur eine Quarklinie umgebogen werden muß. Beide Überlegungen werden
im Experiment bestätigt; für die vielen wichtigen Details muß ich jedoch den
Leser auf die Literatur [Wij79] verweisen.
Übungen
5.4
5.5
Stellen Sie sich vor, Sie erhalten die Aufgabe, die Formfaktoren des
Protons für |q 2 | = 1 GeV2 durch Messen der Winkelverteilung der
Elektronen zwischen 5◦ und 90◦ zu bestimmen. Welche Energien
haben dann die ein- und auslaufenden Elektronen beim größten und
kleinsten Streuwinkel?
Welcher Ladungsverteilung entspricht das Dipolgesetz des elektrischen Formfaktors?
5.3 Inelastische Elektron-Nukleon-Streuung
5.3.1 Der Wirkungsquerschnitt im Quarkmodell
Die Streuung von Elektronen an Quarks ist einer direkten experimentellen
Überprüfung anscheinend nicht zugänglich, da es keine freien Quarks gibt,
wie wir mehrfach betont haben. Von Feynman stammt aber eine scharfsinnige
Überlegung, in der er zeigte, daß ein Proton (oder Neutron) mit sehr hoher
Energie als ein Strahl kollinearer freier Quarks angesehen werden kann. Der
Energieunterschied zwischen einem Proton und einer Anzahl von Quarks,
deren Impulssumme durch den Impuls des Protons gegeben ist, beträgt
2
2
kL,i
+ kT,i
+ m i2 .
(5.50)
∆E = P 2 + M 2 −
i
5
5.3 Inelastische Elektron-Nukleon-Streuung
Der erste Term auf der rechten Seite ist die Energie eines Protons mit dem
Impuls P. Im zweiten Term wird über die beitragenden Quarks summiert, und
die Impulse der Quarks werden in Komponenten kL parallel und kT senkrecht
zum Impuls des Protons aufgespalten. Im Grenzfall sehr hoher Werte von |P|
werden auch die einzelnen kL,i sehr groß. Dann kann die Wurzel in eine Reihe
entwickelt werden, und es folgt
2
+ m i2
M 2 kT,i
∆E =
−
.
2|P|
2kL,i
i
(5.51)
(5.52)
die zugrunde liegende Elektron-Quark-Streuung sichtbar wird.
Wir führen die quantitative Berechnung – wie bereits erwähnt – im infinite
momentum frame durch. Bei hohen Werten von s ist das z.B. das Schwerpunktsystem. Bei einem Elektron-Proton-collider wie HERA, in dem Protonen von
920 GeV auf Elektronen von 28 GeV treffen, kann sogar das Laborsystem ganz
anschaulich als ein solches Bezugssystem gelten. Da das einlaufende Nukleon
als Strahl kollinearer Quarks aufgefaßt wird, bekommt jedes Quark mit dem
Viererimpuls kµ einen bestimmten Bruchteil x des Nukleon-Impulses P µ
kµ = x P µ
k'
q
p
Dies bedeutet aber, daß ∆E in einem Bezugsystem sehr hoher Impulse des
Protons, dem sog. infinite momentum frame, unmeßbar klein wird. Eine verschwindende Verletzung des Energieerhaltungssatzes bedingt aber nach der
Heisenbergschen Unschärferelation eine große Lebensdauer des Zwischenzustandes kollinearer Quarks. Es ist also sehr wahrscheinlich, daß das Proton
in einen solchen Zustand übergeht. Die Elektron-Proton-Streuung wird daher
durch das Diagramm der Abb. 5.12 beschrieben. Das in der Abbildung rechts
unten einlaufende Proton geht im infinite momentum frame in einen Zustand
kollinearer Quarks über (im Bild werden nur die drei Linien der Konstituentenquarks gezeigt). Das Elektron streut an einem dieser Quarks. Es handelt
sich hier um eine typische Weizsäcker-Williams-Näherung, wie wir sie bei der
Behandlung der Bremsstrahlung ausführlich diskutiert haben (Abschn. 3.3.1).
Nach der Streuung hat eines der Quarks einen großen Transversalimpuls
bekommen, die Quarks laufen auseinander, der Fragmentierungsprozeß beginnt. Genau wie bei der Annihilation erfolgen also ein Streuprozeß zwischen
punktförmigen Teilchen bei einem Abstand d 1 fm und die Hadronisierung
bei einem Abstand d 1 fm nacheinander. Auch jetzt wird nicht versucht, die
Übergangswahrscheinlichkeiten in einzelne Endzustände zu berechnen, sondern es werden alle Endzustände X zugelassen. Zusammengefaßt sehen wir
also, daß gerade in der inklusiven Streureaktion
e+ p → e+ X
p'
(5.53)
mit 0 ≤ x ≤ 1. Da wir weiter in der Hochenergienäherung verschwindender
Quarkmassen bleiben, folgt aus k2 = x 2 P 2 , daß im Ansatz (5.53) auch die
Masse des Nukleons im Viererimpuls P µ vernachlässigt wird.
Es soll nun q f (x) die Verteilungsfunktion der Impulse eines Quarks der
Sorte f im Nukleon sein, d.h. q f (x) dx ist die Anzahl von Quarks der Sorte f
k
P
Abb. 5.12
Die inelastische Elektron-Nukleon-Streuung
e + p → e + X im Quarkmodell. Der Graph
enthält die im Text benötigte Definition
der Viererimpulse der beteiligten Teilchen.
Die Blase im oberen Teil der Abbildung
symbolisiert die störungstheoretisch nicht
erfaßbare Verwandlung der Quarks in die
Hadronen des Endzustandes
317
318
5
Elektronen und Quarks
mit relativen Impulsen zwischen x und x + dx, ( f = u, d, ...). Entsprechend
beschreibt q̄ f die Verteilung der Antiquarks. Der Wirkungsquerschnitt der
Elektronenstreuung an den Quarks und Antiquarks im Nukleon folgt nun
unmittelbar mit Hilfe von (3.172)
4πα2
dσ eq
y2 2
=
Q f [q f (x) + q̄ f (x)] dx .
(5.54)
1
−
y
+
dq 2
q4
2
f
Wenn wir jetzt, wie gerade besprochen, über alle Übergangswahrscheinlichkeiten in bestimmte Endzustände summieren, gibt (5.54) den zweifach differentiellen Wirkungsquerschnitt für die Elektron-Nukleon-Streuung
d2 σ eN
y2 F2 (x)
4πα2
1
−
y
+
=
(5.55)
dq 2 dx
q4
2
x
wieder. Hierin wurde gleichzeitig die sog. Strukturfunktion F2 als Abkürzung
für
F2 (x) = x
Q 2f [q f (x) + q̄ f (x)]
(5.56)
f
eingeführt. Zunächst erscheint diese Formel aber noch wenig hilfreich, da die
Variable y gemäß (3.168) im Elektron-Quark-System definiert ist. Außerdem
wird der Wirkungsquerschnitt als Funktion des Quarkimpulses in einem bestimmten Bezugssystem angegeben, während man experimentell gewohnt ist,
ihn in Abhängigkeit von q 2 und W, der invarianten Masse der erzeugten
Hadronen zu messen.
Die beiden dimensionslosen Variablen x und y lassen sich aber problemlos durch Invarianten des Elektron-Nukleon-Streuprozesses ausdrücken.
Aufgrund der Relation kµ = x P µ folgt aus (3.168) unmittelbar
y=
q·P
,
p· P
(5.57)
und damit bleibt insbesondere die Beziehung (5.26) für ein ruhendes target
weiterhin richtig. Aus der Viererimpulserhaltung q + k = k am Photon-QuarkVertex berechnet man sofort
q 2 + 2q · k = 0
(5.58)
und daher
x=
|q 2 |
.
2q · P
(5.59)
Da die invariante Masse der erzeugten Hadronen aber durch
W 2 = (q + P)2
(5.60)
definiert ist, wird die Variable x sehr einfach aus q 2 und W 2 ,
x=
|q 2 |
,
W 2 + |q 2 | − M 2
(5.61)
5
5.3 Inelastische Elektron-Nukleon-Streuung
berechnet. Hieraus ergibt sich, daß der Wertebereich von x auf
0≤x≤1
F2
0,5
(5.62)
eingeschränkt ist, wie es sein muß, da x ja anschaulich dem Impulsbruchteil
der Quarks im infinite momentum frame entspricht. Der Grenzfall x → 1 wird
für die elastische Streuung, W = M, erreicht.
Aus (5.57) und (5.59) können wir noch einen nützlichen Zusammenhang
zwischen x und y ableiten,
|q 2 | = 2xy p · P = xys0 ,
(5.63)
wobei s0 = s − M 2 in s übergeht, wenn M 2 vernachlässigt wird. Insbesondere
gilt s0 = 2E M für Experimente mit ruhendem Target und s0 = 4E E p an einem
Elektron-Proton-Speicherring wie HERA.
Die Beziehung (5.55) enthält einige sehr wichtige physikalische Aussagen:
18°
10°
6°
26°
0,4
0,3
0,2
x = 0,25
0,1
0
0
2
4
6
8
|q2 |/GeV2
Abb. 5.13
Das Skalenverhalten der Strukturfunktion
F2 bei x = 0,25 und 1 ≤ |q 2 | < 8 GeV2 , wie
es in den Experimenten am SLAC gefunden
wurde
– Da 1 − y + y2 /2 auf Werte zwischen 0,5 und 1 beschränkt ist, fällt der
inelastische Wirkungsquerschnitt bei festem x nur wie etwa 1/q 4 ab. Vergleichen Sie dies mit dem 1/q 12 Gesetz der elastischen Streuung!
– Die durch den ,,punktförmigen“ Querschnitt (3.172) geteilten Meßwerte hängen nur noch von x also dem Verhältnis von |q 2 | zu (|q 2 | + W 2 )
und nicht separat von q 2 und W 2 ab. Man nennt dies ,,Skalenverhalten“. Ein besonders schönes Beispiel aus der Frühzeit der Experimente
zur Elektron-Proton-Streuung zeigt das Skalenverhalten der Strukturfunktion F2 in eindrucksvoller Weise (Abb. 5.13).
– Durch Messungen der inelastischen Elektron-Nukleon-Streuung kann man
experimentell die Impulsverteilung der Quarks im Nukleon bestimmen. Die
Bewegung der Quarks im Nukleon läßt sich fast wie in einem Mikroskop
beobachten.
Das Skalenverhalten der Strukturfunktion F2 wurde 1968 am SLAC durch
Messungen der Elektronenstreuung an Wasserstoff entdeckt.7 Die Größe des
Wirkungsquerschnitts und der schwache Abfall mit dem Impulsübertrag waren ungeheuer überraschend. Sehr allgemeine theoretische Überlegungen von
Bjorken ließen skalierende Strukturfunktionen für große |q 2 | und W 2 erwarten [Bjo79]. Die Variable x ist deshalb auch als Bjorkensche Skalenvariable
bekannt. Die Elektronenstreuung bei großen |q 2 | und großen W 2 , aber nicht
zu kleinen x-Werten, wird häufig als ,,tief inelastisch“ bezeichnet.8 Ähnlich
wie bei der Elektron-Positron-Annihilation zeigen sich aber die wesentlichen
Züge der durch die Quarks bestimmten Physik schon bei relativ geringen
Werten von |q 2 | und W 2 .
5.3.2 Allgemeine Form des Wirkungsquerschnitts
Bevor wir die Messungen von F2 diskutieren, müssen wir uns noch weiter mit
der wichtigen Kinematik der Elektron-Nukleon-Streuung beschäftigen.
Bei der Diskussion der elastischen Streuung haben wir gesehen, daß es
zwei Formfaktoren gibt. Ebenso ist i.allg. die inelastische Elektron-NukleonStreuung durch zwei Strukturfunktionen F1 und F2 bestimmt. Ihre Definition
erfolgte historisch durch Berechnung der allgemeinsten Form des Produkts
7 Die
Amerikaner Jerome F. Friedmann (geb.
1930) und Henry W. Kendall (1926–1999)
sowie der Kanadier Richard E. Taylor (geb.
1929) erhielten für diese Entdeckung 1990 den
Nobelpreis für Physik.
8 Wahrscheinlich eine unpassende Übersetzung
des englischen deeply inelastic scattering.
319
320
5
Elektronen und Quarks
von zwei elektromagnetischen Hadronströmen [Bar97]. In der hier verwendeten modellmäßigen Ableitung bekommt man eine zweite Strukturfunktion,
wenn man neben den Quarks als weitere elementare Konstituenten (Partonen)
des Protons noch geladene Spin 0-Teilchen zuläßt. Denn es ist a priori nicht
sicher, daß es im Nukleon nur Fermionen als Konstituenten gibt. Mit Hilfe
der Beziehung (5.48) berechnet man – entsprechend dem Vorgehen bei der
Ableitung von (5.55) – den Beitrag der skalaren Partonen zu
d2 σ eN
4πα2
= 4 (1 − y)
Q 2g pg (x) dx ,
2
dq
q
g
(5.64)
wobei pg (x) die Verteilungsfunktion der skalaren Partonen im Nukleon ist.
Die Flavorsorte g dieser hypothetischen Partonen hat natürlich nichts mit den
schon bekannten Quarks zu tun, und die Summe erstreckt sich über Teilchen
und Antiteilchen. Mit den Definitionen
F2 =
Q 2f x[q f (x) + q̄ f (x)] +
Q 2g x pg (x)
(5.65)
g
f
und
F1 =
1
f
2
Q 2f [q f (x) + q̄ f (x)]
(5.66)
folgt bei gleichzeitigem Übergang zu den Differentialen dq 2 und dx die
Basisformel der inelastischen Elektron-Nukleon-Streuung
4πα2 d2 σ eN
2
2
2
(x,
q
)
+
xy
F
(x,
q
)
.
(5.67)
=
(1
−
y)F
2
1
dq 2 dx
q4 x
Hierin haben wir noch eine Abhängigkeit der Strukturfunktionen von q 2 zugelassen, die im Quarkmodell nicht auftritt. Dieses entspricht offenbar dem
Spezialfall
2xF1
F2
1,5<|q2 |<4 GeV2
5<|q2 |<11 GeV2
2
2
12<|q |<16 GeV
1,5
1
Spin 2
1,0
0,5
Spin 0
0
0,5
x 1,0
Abb. 5.14
Experimenteller Test der Callan-Gross-Relation
pg (x) = 0
(5.68)
für alle g, also
F2 (x) = 2xF1 (x) .
(5.69)
Die letzte Beziehung ist als Callan-Gross-Relation bekannt. Die Abb. 5.14
demonstriert in wohl überzeugender Weise, daß die geladenen Partonen im
Nukleon den Spin 1/2 tragen! Genauere Messungen zeigen geringfügige, aber
systematische Abweichungen von der Callan-Gross-Relation auf. Im Rahmen
der QCD ist es jedoch nicht mehr nötig, auf Spin 0-Partonen zurückzugreifen.
Die Abstrahlung von Gluonen, also eine typische QCD-Korrektur, wie sie
schon bei der Elektron-Positron-Vernichtung besprochen wurde, führt zu einer kleinen, berechenbaren Modifikation der Beziehung (5.69). Eine weitere
Möglichkeit, die Callan-Gross-Relation zu ändern, besteht darin, die strikte
Kollinearität der einlaufenden Quarks aufzugeben. Diese bekommen also den
typischen mittleren Transversalimpuls von 300 MeV, der dem Einschluß der
Quarks in einem Nukleon mit dem Radius 1 fm entspricht.
5
5.3 Inelastische Elektron-Nukleon-Streuung
Die inelastische Elektron-Nukleon-Streuung läßt sich auch als Absorption
virtueller Photonen interpretieren. In dieser Interpretation nimmt z.B. der
Querschnitt für die Streuung von Elektronen an einem Proton oder Neutron
die intuitiv ansprechende Form
d2 σ eN
= Γt σt (q 2 , W 2 ) + Γ σ (q 2 , W 2 )
dq 2 dy
(5.70)
an. Hierin ist Γt dq 2 dy die Anzahl transversal polarisierter Photonen, die
von einem Elektron abgestrahlt werden, das im Intervall dq 2 dy beobachtet
wird. Entsprechend ist der Flußfaktor Γ für die longitudinalen Photonen
definiert. σt und σ sind die zugehörigen totalen Photoabsorptionsquerschnitte
der Reaktion γ ∗ + N → X, worin γ ∗ ein virtuelles Photon bedeutet.
Unter Ausnutzung der Definitionen
2xF1 =
|q|2
σt
4π 2 α
(5.71)
und
|q|2
(σt + σ )
(5.72)
4π 2 α
finden wir durch Vergleich von (5.67) mit (5.70) unter Zuhilfenahme von
Γ = Γt
α
[1 + (1 − y)2 ]
Γt =
(5.73)
2π|q 2 |y
F2 =
bzw.
=
2(1 − y)
.
1 + (1 − y)2
(5.74)
Diese Gleichungen sind in der Form identisch zum Flußfaktor (3.248) und
zum Polarisationsparameter (3.250) der QED, in denen z der Impulsbruchteil
des von einem schnellen Elektron abgestrahlten Photons war. Mit q µ = z pµ
folgt aus (5.57) in der Tat y = z.
Viele Anwender bevorzugen die Darstellung des Querschnitts (5.70) in
Abhängigkeit von den Differentialen dΩ und dE . Die Umrechnung ist mit
Hilfe der Beziehung
dq 2 dx
Ex
=
dΩ dE
πy
(5.75)
leicht möglich. Diese ist sowohl im Ruhesystem des Protons als auch in einem
Bezugssystem hoher Nukleon-Impulse (also z.B. im HERA-System oder im
Schwerpunktsystem) gültig.
Vertiefung
Der in (5.71) und (5.72) definierte Zusammenhang zwischen Strukturfunktionen und Wirkungsquerschnitten ist nicht zwingend. Die von L. Hand
ursprünglich für die Elektronenstreuung an ruhenden Protonen abgeleiteten
Flußfaktoren [Han63] lauten
321
322
5
Elektronen und Quarks
Γt =
1
αK E 2π 2 |q 2 |E 1 − 1
|q 2 | + ν2
tan2 (Θ/2) .
=
1
+
2
|q 2 |
(5.76)
Sie beschreiben das Spektrum der Photonen, die von einem im Phasenraumelement dΩ dE nachgewiesenen Elektron stammen. In diesen Formeln
sind die Größen ν und K durch
ν = E − E ,
(5.77)
bzw.
|q 2 |
(5.78)
2M
definiert. Ersichtlich ist K die Energie eines virtuellen Photons, die für
ruhende Nukleonen zum selben Wert von W führt wie die Absorption eines
reellen Photons der Energie ν. Sie wird daher äquivalente Photonenergie
genannt. Die Handschen Formeln führen zum Zusammenhang
K =ν−
2xF1 =
|q|2
σt (1 − x)
4π 2 α
(5.79)
und
|q|2
(σt + σ )(1 − x)
(5.80)
4π 2 α
zwischen
√ Wirkungsquerschnitten und Strukturfunktionen, falls Terme mit
M s vernachlässigt werden.
F2 =
Die totalen Querschnitte σt und σ (und damit auch F1 und F2 ) hängen neben derSchwerpunktsenergie W natürlich im allgemeinen Fall noch von der
Masse q 2 der virtuellen Photonen ab. Wir haben hingegen schon weiter oben
abgeleitet, daß im Quarkmodell die Wirkungsquerschnitte nur noch Funktionen der Skalenvariablen x sind. Beim Übergang vom einfachen Quarkmodell
zur QCD wird jedoch das Skalenverhalten durch die Abstrahlung von Gluonen
in einer wohldefinierten Weise gebrochen. Eine ausführlichere Behandlung der
QCD-Korrekturen muß jedoch noch bis zum übernächsten Abschnitt warten.
In (5.70) ist auch der Übergang zur sog. Photoproduktion enthalten, d.h.
zur Erzeugung von Hadronen durch Reaktionen der Art
γ +N → X ,
(5.81)
wie sie an Beschleunigern, die Strahlen hochenergetischer Photonen erzeugen,
gemessen werden. Im Grenzfall |q 2 | → 0 verschwindet σ , da reelle Photonen keine longitudinale Feldkomponente haben. Der transversale Querschnitt
σt (W 2 , q 2 ) geht in den Wirkungsquerschnitt σγN (W 2 ) der Photoproduktion
über. In dieser Näherung gilt W 2 = ys bei Vernachlässigung der Nukleonenmasse, und es kann über |q 2 | in (5.70) integriert werden. So wird die für
5
5.3 Inelastische Elektron-Nukleon-Streuung
Experimente mit Elektronenstrahlen wichtige Beziehung
dσ
= f γ/e σγN (y)
dy
(5.82)
gewonnen. Der hier auftauchende Flußfaktor f γ/e , also die Verteilungsfunktion der Photonen im Elektron, ist identisch zur QED-Formel (3.243) mit den
Ersetzungen z → y und k2 → q 2 .9 Der Maximalwert von |q 2 | in der Integration muß den jeweils aktuellen experimentellen Bedingungen entnommen
werden, die festlegen, bis zu welchen Winkeln die gestreuten Elektronen
berücksichtigt werden.
5.3.3 Modelle und Ergebnisse für F2eN
Da das Proton die Wellenfunktion |uud hat, könnte man ganz naiv erwarten,
daß jedes der drei Quarks ein Drittel des Impulses trägt. Dieser Vorstellung entspricht die δ-funktionsartige Strukturfunktion der Abb. 5.15a. Ganz ähnlich
wie in der Kernphysik bewirkt die Bindung im Potential jedoch eine Verep
schmierung dieser Linie durch die Fermi-Bewegung, so daß F2 vielleicht
eher wie in Abb. 5.15b aussehen wird. Die Verteilung ist stark asymmetrisch,
was zum Teil darauf zurückzuführen ist, daß F2 proportional zum Produkt
xq f (x) ist.
Die Bindung wird durch Gluonaustausch zwischen den Quarks bewirkt.
Neben den Prozessen der Abb. 5.16a werden im Nukleon dann aber auch Reaktionen der Art der Abb. 5.16b ablaufen. Dies bedeutet, daß die Wellenfunktion
|uud zu einfach ist und durch
| p = |uud + ūu + d̄d + s̄s + ...
F2
a)
1/3
F2
1 x
b)
(5.83)
ersetzt werden muß. Die ursprünglichen u- und d-Quarks (die Konstituentenquarks) nennen wir in Anlehnung an den chemischen Sprachgebrauch
Valenzquarks, die durch Gluonabstrahlung erzeugten hingegen ,,Seequarks“.
Natürlich erwarten wir, daß diese ein relativ weiches Impulsspektrum haben
werden, da sie durch Strahlungsprozesse erzeugt werden. Eine Verteilungsfunktion qs (x) ∼ 1/x der Seequarks, wie sie dem Spektrum (3.259) der
Bremsstrahlung entspricht, führt zu einem konstanten Beitrag zu F2 und
daher zu einer Gestalt der Strukturfunktion (Abb. 5.15c), die ungefähr den
Messungen bei kleinen |q 2 | und x-Werten ≥ 10−2 entspricht.
Der Zusammenhang (5.56) zwischen F2 und den Verteilungsfunktionen
der Quarks erlaubt uns, aus den Messungen wichtige Schlüsse über diese
Funktionen zu ziehen. Unter Vernachlässigung der Beiträge schwerer Quarks
können wir für die Protonstrukturfunktion zunächst
ep
F2 = x 4/9[u(x) + ū(x)] + 1/9[d(x) + d̄(x)] + 1/9[s(x) + s̄(x)] (5.84)
ansetzen. Die Normierungsbedingung der Quarkverteilungsfunktionen wird
durch die Wellenfunktion des Protons zu
1 x
F2
c)
1 x
Abb. 5.15a–c
Der qualitative Verlauf der Strukturfunktion F2 als Funktion von x. Die einzelnen
Figuren werden im Text erläutert
9 Natürlich
gilt wegen der Universalität der
Photon-Lepton-Wechselwirkung auch f γ/e =
f γ/µ .
323
324
5
Elektronen und Quarks
Abb. 5.16a,b
(a) Gluonaustausch und (b) Gluonabstrahlung im Nukleon
a)
b)
(u − ū) dx = 2
(d − d̄) dx = 1
(s − s̄) dx = 0
(5.85)
festgelegt. Damit wird garantiert, daß im Proton im Mittel zwei u- und ein
d-Quark vorhanden sind.
Wir bezeichnen nun mit u| p die Amplitude, ein u-Quark im Proton
zu finden. Die Verteilungsfunktion u(x) ist proportional zum Quadrat dieser
Amplitude. Entsprechende Relationen gelten auch für die anderen Funktionen
d(x), s(x) usw. Die SU2-Transformation U = U2 (π) verwandelt ein Proton in
ein Neutron und ein u-Quark in ein d-Quark. Mit
u| p = u|U −1 U| p
= d|n
(5.86)
gilt also u p = d n , oder, da die nichtindizierten Verteilungsfunktionen für das
Proton gelten sollen,
d n (x) = u(x) .
(5.87)
Die Strukturfunktion des Neutrons wird aufgrund dieser Rotationen in die
Form
F2en = x 1/9[u(x) + ū(x)] + 4/9[d(x) + d̄(x)] + 1/9[s(x) + s̄(x)] (5.88)
gebracht.
Aus den Parametrisierungen (5.84) und (5.88) wird klar, daß durch Messung der Elektron-Nukleon-Streuung allein die einzelnen Anteile u, ū, ...
nicht ohne weitere Annahmen voneinander getrennt werden können. Aus der
ep
Differenz F2 − F2en läßt sich aber mit Hilfe solcher Annahmen der Beitrag
5
5.3 Inelastische Elektron-Nukleon-Streuung
der Valenzquarks bestimmen. Dazu teilen wir die u- und d-Funktionen in
einen Valenz- und einen Seeanteil auf,
u = uv + us
d = dv + ds .
(5.89)
Die strange-Quarks und alle Antiquarks finden wir nur im See. Mit der
zusätzlichen Annahme, daß die Verteilung der Seequarks für alle Quarksorten
gleich ist, folgt jetzt sofort
x
ep
F2 − F2en = (u v − dv ) ,
(5.90)
3
und wenn wir weiter vereinfachend ansetzen, daß der Unterschied zwischen
u v und dv nur in der Normierung liegt, ist die rechte Seite dieser Gleichung
durch xu v /6 gegeben. Die experimentellen Ergebnisse der Abb. 5.17 folgen
sehr schön den qualitativen Überlegungen, die wir schon weiter oben angestellt
haben (Abb. 5.15).
Besonders interessant ist das Integral der Strukturfunktionen. Da die
Summe der Partonen-Impulse gleich dem Nukleon-Impuls sein muß, gilt
1
x(u + ū + d + d̄ + s + s̄) dx = 1 − ε ,
(5.91)
0
wobei ε der Bruchteil des Impulses ist, der von neutralen Partonen, also
z.B. den Gluonen, getragen wird. Weil die strange-Quarks nur im See vorkommen, sollten sie sehr wenig zur Impulssumme beitragen. Messungen der
p
n
F2 – F2
0,10
0,08
0,06
0,04
0,02
0
–0,02
0
0,2
0,4
0,6
0,8
x
Abb. 5.17
Der aus den Proton- und Neutrondaten
gewonnene Beitrag der Valenzquarks zu F2
325
326
5
Elektronen und Quarks
inelastischen Neutrino-Nukleon-Streuung (Abschn. 6.2.6) zeigen, daß der Anteil der strange-Quarks zur Impulssumme (5.91) nur etwa 6 % beträgt. Aus
der Summe von (5.84) und (5.88) erhalten wir daher bei Vernachlässigung der
strange
Quarks
9
ep
(F2 + F2en ) dx = 1 − ε .
(5.92)
5
Die experimentellen Untersuchungen dieser Summenregel geben einen Wert
von etwa 0,54 ± 0,04 für die linke Seite der Gleichung. Fast die Hälfte des
Nukleon-Impulses steckt also in den Gluonen. Dieses überraschende Ergebnis zeigt beispielhaft, wie sich aus den Experimenten der inelastischen
Lepton-Nukleon-Streuung fundamentale Aussagen über Quarks und Gluonen
im Inneren der Nukleonen gewinnen lassen.
ep
Auch aus der Differenz von F2 und F2en kann eine interessante Summenregel gewonnen werden, die auf Gottfried zurückgeht. Dazu wird das
Integral
1
dx
ep
IG = (F2 − F2en )
(5.93)
x
0
betrachtet. Nach Einsetzen von (5.84) und (5.88) wird daraus mit Hilfe von
(5.85) die Beziehung
1
1 2
(ū − d̄) dx
(5.94)
IG = +
3 3
0
abgeleitet. Falls wieder ū(x) = d̄(x) angenommen wird, gilt demnach IG =
1/3. Da der gemessene Wert des Integrals auf der rechten Seite von (5.93)
aber deutlich unter 1/3 liegt, wird in neueren Analysen nicht mehr von einer
Gleichheit der ū- und d̄-Verteilungen ausgegangen.
Messungen der Strukturfunktionen können auch mit Neutrinostrahlen
gemacht werden. Der Beitrag einzelner Quarksorten läßt sich mit dieser
Methode sogar besser isolieren. Darauf werden wir in Abschn. 6.2.6 noch
zurückkommen. Die meisten Experimente wurden bei |q 2 | < 10 GeV2 und
x-Werten > 0,05 durchgeführt. In diesem kinematischen Bereich ist das Skalenverhalten der Strukturfunktionen experimentell gut erfüllt, und es macht
Sinn, aus solchen Messungen die Dichteverteilungen q(x) zu bestimmen.
Eine beliebte Parametrisierung [Eic86] benutzt den in (5.89) und den darauf
folgenden Zeilen beschriebenen Ansatz. Das Ergebnis ist in Abb. 5.18 zusammen mit der Gluondichte, auf deren Bestimmung wir im nächsten Abschnitt
eingehen, wiedergegeben. In Formeln lautet es:
xu v = 1,78 x 0,5 (1 − x 1,51 )3,5
1,0
xg
xuv
0,5
xdv
xu xs
0
0
xdv = 0,67 x 0,4 (1 − x 1,51 )4,5
0,4
0,8
x
Abb. 5.18
Die Dichteverteilungen von Quarks und
Gluonen nach Eichten et al. [Eic86]. Aufgetragen wurde xq(x) bzw. xg(x) als Funktion
von x
xu s = 0,182 (1 − x)8,54
xds = xu s
xss = 0,081 (1 − x)8,54
xg = (2,62 + 9,17x)(1 − x)5,9 .
(5.95)
5
5.3 Inelastische Elektron-Nukleon-Streuung
Diese empirischen Darstellungen dienen u.a. zur Abschätzung der Zählraten
von Reaktionen, an denen Quarks und Gluonen beteiligt sind.
5.3.4 QCD-Korrekturen
Die Korrekturen niedrigster Ordnung der QCD zur Elektronenstreuung im
Quarkmodell berücksichtigen die Abstrahlung von Gluonen von dem am harten Streuprozeß teilnehmenden Quark. Die zugehörigen Diagramme sind in
Abb. 5.19 zu sehen. Der harte Subprozeß ist jetzt die inelastische Streuung
e
p
e
p
b)
a)
Abb. 5.19a,b
QCD-Korrekturen zur inelastischen Elektronenstreuung im Quarkmodell. Die Diagramme beschreiben die Abstrahlung eines
Gluons vom (a) ein- bzw. (b) auslaufenden
Quark
e + q → e + q + g (Gluonbremsstrahlung) eines Elektrons an einem Quark
der Sorte f mit dem Impulsbruchteil ξ. Der Beitrag dieser Diagramme zum
Gesamtwirkungsquerschnitt kann analog zu (5.70) formuliert werden,
d2 σ eN
= Γt
dq 2 dy
1
tˆ ξ=x
dσt
q f (ξ)
dtˆ dξ + Γ
dtˆ
1
q f (ξ)
tˆ
x
dσ
dtˆ dξ .
dtˆ
(5.96)
Hierin sind dσt / dtˆ bzw. dσ / dtˆ die differentiellen Wirkungsquerschnitte für
den virtuellen QCD-Compton-Effekt
γ∗ +q → g+q
(5.97)
∗
im γ q Subsystem. Im entsprechenden Ausdruck für die Antiquarks werden
die Dichten q f (ξ) durch die Antiquarkdichten q̄ f (ξ) ersetzt. Um die Formeln aber einigermaßen übersichtlich zu halten, beschränken wir uns in der
Herleitung der QCD-Formeln auf die Quarks.
Zunächst beschäftigen wir uns noch etwas mit der Kinematik dieser Reaktion und betrachten dazu das allgemeine Diagramm der Abb. 5.20. Aus der
Erhaltung des Viererimpulses folgt sofort
(q + k)2 = ŝ ,
(5.98)
wobei wie immer mit masselosen Quarks gerechnet wurde.10 Wir definieren
nun die dimensionslose Variable
|q 2 |
xp =
(5.99)
2q · k
und erhalten mit (5.98)
xp =
|q 2 |
.
ŝ + |q 2 |
(5.100)
k'
q
k
Abb. 5.20
Die QCD-Compton-Streuung γ ∗ q → gq
10 Das Symbol q bezeichnet hier wie immer
den Viererimpuls des ausgetauschten Photons, in der Reaktionsgleichung (5.97) steht
es als Abkürzung für ,,Quark“. Das zeigt
nochmal den Konflikt der Wahl zwischen
gängigen Bezeichnungen und Eindeutigkeit
der verwendeten Symbole.
327
328
5
Elektronen und Quarks
Aus dem Vergleich mit (5.61) für M = 0 ergibt sich der Wertebereich von x p ,
x ≤ xp ≤ 1 ,
(5.101)
da ŝ Werte zwischen 0 und W 2 annehmen kann.
Wir haben mit ξ den Bruchteil des Nukleonen-Impulses bezeichnet, den das
einlaufende Quark übernimmt. Einsetzen in (5.59) und Vergleich mit (5.99)
ergibt
x
ξ=
(5.102)
xp
mit x ≤ ξ ≤ 1. Bitte beachten Sie, daß die Bjorken-Variable x nur im Fall
der elastischen Elektron-Quark-Streuung als Impulsbruchteil des einlaufenden Quarks identifiziert werden kann, dieser Grenzfall ist in (5.102) für ŝ = 0
enthalten. Die abgeleiteten kinematischen Relationen werden besonders anschaulich im Falle der Strahlung im Anfangszustand (initial state radiation),
wie sie in Abb. 5.19a zu sehen ist. Das Quark mit dem Impulsbruchteil ξ > x
strahlt ein Gluon ab. Danach hat das mit dem Elektron wechselwirkende
Quark einen Impulsbruchteil x p vom einlaufenden Quark oder x vom Proton
übernommen.
Der Wirkungsquerschnitt dσt / dtˆ kann nicht unmittelbar aus (3.234) entnommen werden, da in dieser Summe auch die Anteile von longitudinal
polarisierten Photonen enthalten sind. Dieser Anteil beträgt
T2 =
4|q 2 |tˆ
(ŝ + |q 2 |)2
(5.103)
und muß daher abgezogen werden. Mit q 2 = −|q 2 | lautet das Resultat
8πQ 2f ααS
dσt
1
û ŝ 2q 2 tˆ
4q 2 tˆ
=
+ +
+
.
(5.104)
3
(ŝ + |q 2 |)2 ŝ û
ŝ û
ŝ + |q 2 |
dtˆ
Beim Nachrechnen beachten Sie bitte, daß die Summe der Amplitudenquadrate zur Mittelung über die Polarisation der transversalen Photonen durch
vier geteilt wurde und außerdem e4 wieder durch e2 Q 2f g2 cF zu ersetzen ist. Im
Gegensatz zur Annihilation müssen wir jetzt über die Farben der einlaufenden
Quarks mitteln. Der Farbfaktor cF beträgt daher 4/3 und nicht 4.
Die folgende Diskussion der Integrale in (5.96) wird durchsichtiger, wenn
ŝ durch x p und tˆ durch
z=
k · k
tˆ
=
q ·k
ŝ + |q 2 |
(5.105)
ersetzt wird. Man überzeugt sich leicht davon, daß z gemäß
1 − cos Θ ∗
(5.106)
2
durch den Streuwinkel zwischen dem Gluon und dem Photon im γqSchwerpunktsystem ausgedrückt werden kann. Damit sind auch die Grenzen
0 ≤ z ≤ 1 unmittelbar einsichtig.
z=
5
5.3 Inelastische Elektron-Nukleon-Streuung
Mit Hilfe dieser Variablen nimmt (5.104) die Gestalt
8πQ 2f ααS x p
1 + x 2p z 2
dσt
=
+ (1 − x p )(1 − z)
dz
3
|q 2 | (1 − x p )(1 − z)
(5.107)
an. Die zur Berechnung von (5.96) nötigen Integrale lassen sich nun nicht
ohne weiteres ermitteln, da in (5.107) wiederum die uns inzwischen vertrauten
Divergenzen auftauchen. Die Divergenz für z → 1 entspricht dem u-Pol der
Compton-Streuung mit reellen Photonen, das bedeutet hier Θ ∗ = π oder im
eq-System die Abstrahlung eines Gluons kollinear mit dem einlaufenden
Quark. Der Pol bei x p → 1 entspricht ŝ → 0 und bedeutet, daß das Gluon
entweder sehr niederenergetisch (Infrarot-Divergenz) oder (im eq-System)
kollinear mit dem auslaufenden Quark wird.
In der leading log Näherung (LL) werden nur die Terme berücksichtigt,
die für x p → 1 und z → 1 groß werden, (5.107) wird also durch
8πQ 2f ααS x p
1 + x 2p
dσt
=
(5.108)
dz
3
|q 2 | (1 − x p )(1 − z)
ersetzt. Die Divergenz bei z → 1 ist nicht vorhanden, wenn die Masse µ
der Quarks berücksichtigt wird, da dann die obere Grenze von z durch 1 −
2µ2 x p /|q 2 | definiert ist. Die Masse eingeschlossener Quarks ist insbesondere
für die u- und d-Quarks keine wohldefinierte Größe, und wir fassen daher µ
als eine relativ frei wählbare Energieskala auf, die zur Regularisierung des
divergenten Integrals über z dient. Die Durchführung der Integration hat nun
2 x p qq
|q |
2
σt = 2πQ f ααS 2 P ln
(5.109)
|q |
µ2
mit
4 1 + x 2p
P qq =
(5.110)
3 1− xp
zum Ergebnis. Die Splitting-Funktion P qq der Quarks ist auch schon altbekannt. Sie wird hier als Funktion des Impulsbruchteils x p angegeben und ist
– bis auf den Farbfaktor 4/3 – mit der Splitting-Funktion P ee der QED aus
(3.286) identisch. Genau genommen sollte das Argument des Logarithmus
noch einen Faktor 2x p enthalten, der aber ebenfalls vernachlässigt wird, da
P qq nur für x p → 1 große Beiträge liefert und µ frei wählbar ist.
Der longitudinale Querschnitt σ enthält keine Divergenzen und kann in der
LL-Näherung vernachlässigt werden. Den Zusammenhang (5.72) zwischen
Wirkungsquerschnitt und Strukturfunktion bedenkend, liefert (5.109) für jede
Quarksorte den Beitrag
αS 2 |q 2 |
∆F2 =
Q ln 2
2π f
µ
1
x p P qq (x p )q f (ξ) dξ
(5.111)
x
der Diagramme in Abb. 5.19 zu F2 . Die verbleibende kollineare und infrarote
Divergenz bei x p = 1 wird wieder durch Hinzunahme der virtuellen Korrekturen behoben. Die Diskussion ist ziemlich kompliziert, aber wie in der QED
329
330
5
Elektronen und Quarks
läuft die Berücksichtigung dieser Korrekturen auf die Substitution von P qq
qq
durch die regularisierte Splitting-Funktion P+ hinaus. Diese ist im Kasten auf
S. 225f. erläutert. Unter dem Integral von (5.111) ersetzen wir noch ξ durch
x p und wechseln von der Strukturfunktion direkt zu den Quarkdichten, die
demnach jetzt durch
1 dx p
αS |q 2 |
x
qq
2
ln 2
qf
(5.112)
q f (x, q ) = q f (x) +
P+ (x p )
2π
µ
xp
xp
x
gegeben sind.
Intuitiv scheint es nun vielversprechend zu sein, die Dichten q f (x) auf
der rechten Seite mit den bei kleinen |q 2 | gemessenen Verteilungen zu identifizieren, da diese ja empirisch gut das Skalenverhalten erfüllen und sich
relativ einfach parametrisieren lassen (5.95). Dies ist aber nicht konsequent,
da wir nicht wissen, bei welcher Skala die Gluonabstrahlung beginnt. Es ist
im Gegenteil sogar so, daß q f (x) in (5.112) eine prinzipiell nichtmeßbare
,,nackte“ Partondichte ist, ganz ähnlich wie die nackte Ladung der QED aus
Abschn. 3.1.4. Wir identifizieren daher jetzt die Ausgangsverteilungen mit
den renormierten Quarkdichten q f (x, µ2F ), die mit den nackten Verteilungen
gemäß (5.112)
1 dx p
αS µ2F
x
qq
2
q f (x, µF ) = q f (x) +
ln
qf
P+ (x p )
(5.113)
2π µ2
xp
xp
x
verknüpft sind. Diese Renormierung wird so interpretiert, daß die Divergenzen der Integrale bei der sog. Faktorisierungsskala µF in die Definition der
Partondichten absorbiert werden. Der Vergleich mit (5.112) zeigt nun, daß bis
auf Terme der Ordnung αS2 die Partondichte q f (x, q 2 ) aus der Dichte q f (x, µ2F )
mit Hilfe von
1 dx p
αS |q 2 |
x
qq
2
2
qf
, µ2F P+ (x p )
q f (x, q ) = q f (x, µF ) +
ln 2
2π
xp
xp
µF
x
(5.114)
berechnet werden kann.
Die letzte Gleichung stellt eine fundamentale Vorhersage der QCD dar.
Ausgehend von gemessenen Verteilungen bei einem beliebigen Wert |q 2 | = µ2F
sind die Quarkdichten bei jedem anderen |q 2 | berechenbar! Man sagt, die
Evolution der Quarkdichten ist durch die QCD festgelegt. Formal entspricht
(5.114) vollständig der Formel (3.131) für die renormierten Ladungen. Diese
Analogie läßt sich noch weiter treiben. Die laufenden Kopplungen genügen
einer Differentialgleichung (Übung auf S. 192). Für q f (x, q 2 ) kann ebenfalls
eine Differentialgleichung gewonnen werden, wenn zunächst die führenden
Logarithmen der Beiträge höherer Ordnung zu (5.114) berechnet werden. Die
gesuchte Integro-Differentialgleichung lautet dann
1 dx p
q 2 dq f (x, q 2 ) αS (q 2 )
x 2
qq
=
qf
, q P+ (x p )
.
(5.115)
2
dq
2π
xp
xp
x
5
5.3 Inelastische Elektron-Nukleon-Streuung
Sie ist in der Struktur identisch zu der Gleichung, die durch Differenzieren
von (5.114) erhalten werden kann, aber auf der rechten Seite finden wir jetzt die
laufende Kopplungskonstante αS (q 2 ) und die Partondichte q f bei der Skala q 2 .
Die Gleichung enthält daher die bemerkenswerte Feststellung, daß die starke
Kopplungskonstante durch Messung der Steigung der Partondichten, also auch
der Steigung von F2 (x, q 2 ), bestimmt werden kann.
Für eine quantitative Analyse der Verletzung des Skalenverhaltens reicht
(5.115) noch nicht aus. Es muß nämlich bedacht werden, daß die Gluonen
im Nukleon und das virtuelle Photon über die Paarerzeugung γ ∗ g → q q̄
zusätzliche Quarks und Antiquarks produzieren, an denen die Elektronen
streuen können. Die Berücksichtigung dieser Photon-Gluon-Fusion ergibt
einen weiteren Term in (5.114), dessen Struktur aber sehr ähnlich zum quarkinduzierten Term ist. Die Quarkdichte wird durch die Gluondichte g ersetzt,
qq
gq
und an die Stelle der Splittingfunktion P+ tritt die Splittingfunktion P+ , die
die Aufspaltung eines Gluons in ein Quark-Antiquark-Paar beschreibt. Der
zusätzliche Term läßt sich vermeiden, wenn Differenzen von Quarkdichten,
wie z.B. u − d, betrachtet werden. Diese sog. non singlet-Verteilungen q NS
bekommen keine Beiträge von der Photon-Gluon-Fusion, da P gq unabhängig
von der Quarksorte ist.11
Experimentell kann die Entwicklung einer Quarkdichte q NS durch die
Betrachtung der non singlet-Strukturfunktion
p
F2NS = F2 − F2n
(5.116)
studiert werden, da die zugehörige Partondichte gemäß (5.90) mit
q NS = u v − dv
(5.117)
angesetzt werden kann.
Die Evolution von q NS ist durch (5.115) bestimmt. Dies ist eine der
berühmten Altarelli-Parisi-Gleichungen [Bar97, Qui83], die häufig auch als
DGLAP-Gleichungen (für Dokshitzer, Gribov, Lipatov, Altarelli und Parisi)
bezeichnet werden.12 Sie stehen ganz im Zentrum quantitativer Analysen
der Nukleonstruktur. Wenn die Beschränkung auf q NS aufgegeben wird,
erhält man ein System gekoppelter Integro-Differentialgleichungen für die
Quarkdichten q, q̄ und die Gluondichte g oder für die Linearkombinationen q NS , q S und g, wobei q S als Singulett-Dichte bezeichnet wird. Dieses
Gleichungssystem wird in vielen Lehrbüchern, z.B. [Bar97] ausführlich
diskutiert.
Infolge der Vernachlässigung aller kleinen Terme ist in der LL-Näherung
automatisch die Callan-Gross-Relation (5.69) erfüllt. In dieser Näherung gilt
also F = 0 und
F2 = x
Q 2f [q f (x, q 2 ) + q̄ f (x, q 2 )] .
(5.118)
f
Es ist aber auch klar, daß ohne diese Vernachlässigung der kleinen Terme eine
QCD-Vorhersage für die longitudinale Strukturfunktion
F = F2 − 2xF1
(5.119)
11 Der
Name non singlet bezieht sich auf
das Verhalten einer solchen Kombination
von Quarkdichten unter Transformationen der
flavor-Symmetriegruppe.
12 Die
bahnbrechende Arbeit [Alt77] von
G. Altarelli und G. Parisi gehört mit über
2000 Zitaten zu den am häufigsten genannten
wissenschaftlichen Veröffentlichungen. Durch
den Namen ,,DGLAP-Gleichung“ werden
auch die Beiträge der russischen Theoretiker
Y.N. Dokshitzer, V.N. Gribov und L.N. Lipatov
gewürdigt.
331
332
5
Elektronen und Quarks
F2NS
0,5
1
x
Abb. 5.21
Qualitative Änderung der Strukturfunktion F2NS mit |q 2 |. Die durchgezogene
Kurve zeigt den Verlauf bei kleinen Impulsüberträgen, während die gestrichelte
Kurve für hohe Werte von |q 2 | gilt
erhalten werden kann. Der longitudinale Anteil der QCD-Compton-Streuung
kann z.B. mit Hilfe von (5.103) berechnet werden. Hinzu kommt noch der
Anteil der Photon-Gluon-Fusionsprozesse. Mit einer quantitativen Behandlung wollen wir aber jetzt ein ohnehin mit Theorie überladenes Kapitel nicht
weiter befrachten, sondern uns noch der anschaulichen Interpretation der
Strukturfunktion und den Meßergebnissen zuwenden.
Die |q 2 |-Abhängigkeit der Strukturfunktion ist intuitiv einsichtig, da mit
wachsenden Werten von |q 2 | ein immer größerer Phasenraum für Strahlungsprozesse zur Verfügung steht. Die Abstrahlung bewirkt, daß es weniger Quarks
mit hohen Impulsen gibt und die Quarks bei kleinen x angereichert werden.
Das Integral der Quarkdichten bleibt dabei konstant, da die Normierungsbedingungen (5.85) auch für die laufenden Quarkdichten
1 qq gültig bleiben. Formal
kann dies in unserer Näherung mit Hilfe von 0 P+ (x p ) dx p = 0 bewiesen
werden. Man erwartet also qualitativ ein Verhalten, wie es in Abb. 5.21 skizziert ist. Dies wird durch die Messungen glänzend bestätigt. Die Abb. 5.22
zeigt die Zusammenfassung der früheren Messungen an Beschleunigern mit
einem externen Elektronen- oder Myonenstrahl und der am ep-collider HERA
gewonnenen Resultate, diesmal aufgetragen als Funktion von |q 2 | mit x als
Parameter zur Unterscheidung der Kurven. Die Präzision der Daten und der
riesige überdeckte Bereich in der |q 2 |, x-Ebene ist beeindruckend. Die eingezeichneten Kurven sind das Resultat einer QCD-Evolutionsanalyse in next
to leading order (NLO), die nicht nur die Beiträge der führenden Logarithmen berücksichtigt. Bei den höchsten x-Werten sieht man eine schwache
Verletzung des Skalenverhaltens, also ein langsames Abfallen der Strukturfunktion F2 für |q 2 |-Werte zwischen 5 und 20 000 GeV2 . Bei x = 0,25, das
ist in der Nähe der Überkreuzung der beiden Kurven in Abb. 5.21, ist F2
praktisch konstant. Interessanterweise wurde das Skalenverhalten der Strukturfunktion gerade bei diesen x-Werten entdeckt (Abb. 5.13). Schließlich wird
für x ≤ 5 · 10−3 eine deutliche Zunahme der Strukturfunktion bei wachsendem |q 2 | gefunden. Auch diese relativ starke Verletzung des Skalenverhaltens
wird hervorragend von der perturbativen QCD beschrieben.
Weil die Brechung des Skalenverhaltens der Strukturfunktionen eine unmittelbare Folge der Gluonstrahlung und der γg-Reaktionen ist, lassen sich
die Gluondichten g(x, q 2 ) durch Analyse der q 2 -Evolution von F2 berechnen.
Eine direktere und vielleicht anschaulichere Methode besteht in der Messung
der inklusiven Photoproduktion von ψ-Mesonen,
γ +p→ψ+X
(5.120)
in Strahlen reeller Photonen. Die experimentelle Signatur der Reaktion ist
ziemlich klar, da man die ψ-Resonanzen durch ihren µ− µ+ -Zerfall rekonstruieren kann. Die Gluonen im Nukleon erzeugen cc̄-Quarks in der Reaktion
der Paarerzeugung (Abb. 5.23a)
13 Außerdem wird auf diese Weise ein Konflikt
mit Yangs Theorem, Abschn. 2.4.7, vermieden,
das den Übergang von zwei Photonen in ein
Vektormeson verbietet.
γ + g → c + c̄ ,
(5.121)
die man häufig auch ,,Gamma-Gluon-Fusion“ nennt. Da das ψ ein Farbsingulett ist, muß zusätzlich ein (weiches) Gluon abgestrahlt werden (Abb. 5.23b).13
5
5.3 Inelastische Elektron-Nukleon-Streuung
Abb. 5.22
Resultate des H1-Experiments am epcollider HERA für die Strukturfunktion F2
zusammen mit Ergebnissen früherer Experimente am ruhenden Proton. Man beachte,
daß die Skala der Abszisse sich ändert
F2 +ci (x)
16
NMC
x = 0,0002 (i = 24)
BCDMS
x = 0,000032
H1 94
x = 0,00005
14
SLAC
H1 95 SVX
x = 0,00008
H1 95 – 96 Preliminary
x = 0,0013 (i = 20)
x = 0,0002
H1 94 – 97 Preliminary (high Q2)
x = 0,00032
12
x = 0,0005
NLO QCD Fit
H1 Preliminary
x = 0,0008
ci(x) = 0,6 ·(i(x) – 0,4)
x = 0,0013
10
x = 0,002
x = 0,0032
x = 0,005
8
x = 0,008
x = 0,013 (i =10)
6
x = 0,02
x = 0,032
x = 0,05
4
x = 0,08
x = 0,13
x = 0,18
2
x = 0,25
x = 0,40
x=0,65(i =1)
0
1
10
10 2
10 3
10 4
10 5
|q2|/GeV 2
333
334
5
Elektronen und Quarks
Abb. 5.23a,b
Die Erzeugung von (a) charm-Quarks und
(b) J/ψ-Mesonen in der Gamma-GluonFusion
J /ψ
c
g
c
g
g
a)
b)
In der Diskussion des letzten Abschnitts haben wir uns vom engen Zusammenhang der Photoproduktion und der Elektronenstreuung bei kleinen
Impulsüberträgen überzeugt. Die Photoerzeugung von cc̄ oder bb̄ in der
Gamma-Gluon-Fusion studiert man daher praktischerweise in der inelastischen Elektronenstreuung bei sehr kleinen Werten von |q 2 |. Solche
Untersuchungen werden z.B. am Elektron-Proton-Speicherring HERA in
Hamburg durchgeführt.
5.3.5 Der Endzustand
Wie in der Elektron-Positron-Vernichtung formieren sich auch im Endzustand
der tief inelastischen Lepton-Nukleon-Streuung die Hadronen zu Jets. Entsprechend der Abb. 5.12 besteht der Endzustand in der niedrigsten Ordnung
aus einem Quark-Jet mit dem Transversalimpuls des gestreuten Elektrons und
einem aus dem Protonrest gebildeten Jet, der im e p-Schwerpunktsystem entlang der Richtung des einfallenden Protons läuft. Um zwischen dem Jet vom
Protonrest und dem Jet aus der harten Streuung zu unterscheiden, werden solche Topologien als (1 + 1)-Ereignisse bezeichnet. Ein bestimmter Bruchteil
der Strahlungsprozesse der Abb. 5.19 und der γ ∗ g → q q̄ Prozesse führt dann
zu (2 + 1)-Jet Ereignissen. Die genaue Zahl dieser Ereignisse hängt natürlich
wieder vom Auflösungskriterium des Klassifizierungsalgorithmus ab.
Die in der Lepton-Nukleon-Streuung erzeugten Jets aus der harten Streureaktion sollten sich nach dem zugrundeliegenden Modell nicht von den Jets
der e− e+ -Annihilation unterscheiden. Ein wichtiger Test darauf besteht in der
Untersuchung der in Abschn. 5.1.3 eingeführten Fragmentierungsfunktionen
Dh (z). Der Bruchteil z des Longitudinalimpulses, den ein Hadron (h) vom
fragmentierenden Quark (q) übernimmt, kann durch
z=
Eh
Eq
(5.122)
angenähert werden. Damit gilt im e− e+ -Schwerpunktsystem
z = E h /E
(5.123)
5
5.3 Inelastische Elektron-Nukleon-Streuung
für die Paarvernichtung e− e+ → q q̄. Im Fall der Lepton-Nukleon-Streuung
gewinnen wir aus dem Ansatz pµh = zkµ die invariante Definition
ph · P
z=
,
(5.124)
k· P
die im Ruhesystem des Nukleons bei Vernachlässigung der Nukleon-Masse
den Wert
z = E h /yE
(5.125)
annimmt.
Insbesondere bei kleinen z-Werten kann es sein, daß ein Hadron aus dem
Proton-Rest mit einem Hadron aus den Quark- (oder Gluon-) Jets verwechselt
wird. In neueren Analysen wird daher die Elektronenstreuung im sog. BreitSystem analysiert. In diesem Bezugsystem erleidet das Elektron keinen Energieverlust, sondern nur eine Richtungsänderung. Es gilt also q 2 = −qB2 bzw.
qBµ = 0, 0, 0, |q 2 | .
(5.126)
e
q
Abb. 5.24
Die Elektron-Quark-Streuung im BreitSystem
Aus der Energie-Impuls-Erhaltung folgt, daß das einlaufende Quark in sich
selbst reflektiert wird (Abb. 5.24), k = −k und
kµ=
|q 2 |/2, 0, 0, |q 2 |/2 .
(5.127)
Hierdurch wird eine maximale Trennung des Protonrests vom gestreuten
Quark bewirkt. Dieses befindet sich in der sog. Strom-Hemisphäre des Koordinatensystems, während die Bruchstücke des Protons in die Rest-Hemisphäre
fliegen. Aus (5.127) folgt unmittelbar
2E h
z= ,
(5.128)
|q 2 |
wobei E h jetzt die Energie des Hadrons im Breit-System ist.
a)
b)
f(z) = 1 z dσ
σ π dz
Elektroproduktion
0,16
D(z)
–
π
D d (vp)
Annihilation
+
0,12
π
D u (µp)
1,0
e–8z (e+e–)
0,08
0,1
0,12
0
0
0,2
0,6
1,0
z
0,2
0,4
0,6
0,8
z 1,0
Abb. 5.25a,b
(a) Verteilung der Longitudinalimpulse von
Pionen in der Elektron-Proton-Streuung
und der e− e+ -Annihilation. (b) Verteilung
der Longitudinalimpulse in der LeptonNukleon-Streuung bei höheren Werten von
|q 2 |. Die durchgezogene Linie repräsentiert
die Daten der Annihilation
335
336
5
Elektronen und Quarks
Schon die Daten eines frühen Experiments [Ber77] (Abb. 5.25a) zeigten
eine überraschend gute Übereinstimmung der Verteilungsfunktionen Dh (z)
bei noch sehr geringen Werten von |q 2 |. Wir bemerken also auch hier wieder,
wie schnell hadronische Korrekturen bei inklusiven Prozessen mit |q 2 | abklingen. Genaue Untersuchungen der Jeteigenschaften aus ganz unterschiedlichen
Streuprozessen wurden in großer Zahl durchgeführt. Sie beweisen, daß die
Hadronisierung der Quarks und Gluonen in der Tat universell ist (Abb. 5.25b).
Übungen
5.6
5.7
Drücken Sie x und y in Abhängigkeit von Energie und Winkel des gestreuten Elektrons in einem Elektron-Proton-Speicherringexperiment
aus.
Leiten Sie (5.75) ab.
5.4 Zwei-Photonen-Physik
Die Elektron-Positron-Paarvernichtung und die Elektron-Myon-Streuung sind
Prozesse mit zwei einlaufenden und zwei auslaufenden Teilchen. In der
Störungstheorie niedrigster Ordnung werden die Querschnitte proportional
zu α2 . Mit der Bremsstrahlung haben wir einen Prozeß proportional zu α3
kennengelernt, und nun diskutieren wir die Reaktion
e− + e+ → e− + e+ + X ,
(5.129)
deren Wirkungsquerschnitt für Baumgraphen proportional zu α4 ist. In dieser Gleichung steht X für einen beliebigen Endzustand, z.B. ein Meson oder
ein Myon-Paar (Abb. 5.26a bzw. 5.26b). Die Abbildungen zeigen, daß der
Endzustand X im Gegensatz zur e− e+ -Annihilation aus zwei virtuellen Photonen erzeugt wird, daher hat dieser Teil der Elektron-Positron-Reaktionen den
Namen Zwei-Photonen-Physik erhalten. Naiverweise würde man vielleicht
vermuten, daß die Wirkungsquerschnitte der Zwei-Photonen-Reaktionen um
einen Faktor α2 (d.h. etwa 20 000) gegenüber der e− e+ -Annihilation unterdrückt sind und daher völlig vernachlässigt werden können. Eine so
pauschale Argumentation ist aber nicht ohne weiteres zulässig, da man zeigen
kann, daß der Wirkungsquerschnitt in bestimmten kinematischen Situationen
e
R
e
Abb. 5.26a,b
Beispiele für Prozesse der Zwei-PhotonenPhysik: (a) Produktion einer Mesonresonanz, (b) Produktion von µ− µ+ -Paaren
a)
e
e
e
e
µ
+
µ
−
e
e
b)
5
5.4 Zwei-Photonen-Physik
große Logarithmen enthält, die bei hohen Elektron- und Positron-Energien E
den Faktor α2 teilweise kompensieren.
5.4.1 Resonanzerzeugung
Als erstes Beispiel betrachten wir die Erzeugung von Mesonen oder
Mesonresonanzen (R) in Zwei-Photonen-Reaktionen, also den Prozeß
e− + e+ → e− + e+ + R .
(5.130)
Dieser wird experimentell an Elektron-Positron-Speicherringen untersucht,
und explizite Angaben von Energien und Winkeln in den folgenden Formeln
beziehen sich daher immer auf das Schwerpunktsystem der einlaufenden Elektronen und Positronen. Die Amplitude der Reaktion (5.130) ist wegen des
Beitrages der beiden Photonpropagatoren proportional zu 1/(q12 q22 ). Sie wird
also groß, wenn die beiden Photonen fast reell sind, daher berechnen wir den
Querschnitt in der Weizsäcker-Williams-Näherung.
Der Wirkungsquerschnitt für die Resonanzproduktion in Zwei-PhotonenReaktionen läßt sich demnach in der Form
R
d2 σ(e− e+ → e− e+ R) = σγγ
(ŝ) f γ/e (z 1 , |q12 |max ) dz 1 f γ/e (z 2 , |q22 |max ) dz 2
(5.131)
R
anschreiben, wobei σγγ
der totale Querschnitt für die Erzeugung einer Reso√
nanz in Abhängigkeit von der Schwerpunktsenergie ŝ im System der beiden
quasireellen Photonen ist. Im Sinne der Weizsäcker-Williams-Näherung sind
in diesem Querschnitt keine Korrekturen enthalten, die die Virtualität der
Photonen berücksichtigen.
Die Verteilungsfunktionen f γ/e der Photonen entnehmen wir (3.244)
α eγ
f γ/e =
P L ,
(5.132)
2π
worin der Logarithmus
L = ln
|qi2 |max (1 − z i )
m 2 z i2
(5.133)
sich in der sogenannten antitag-Konfiguration besonders einfach darstellen
läßt. In dieser Anordnung wird sichergestellt, daß nur solche Ereignisse
berücksichtigt werden, bei denen die auslaufenden Elektronen und Positronen in der Strahlröhre verbleiben. Die zugehörigen maximalen Streuwinkel
2
sind klein (z.B. ≤ 3◦ ), so daß mit |qi2 |max ≈ E 2 (1 − z i )Θi,max
der Logarithmus
durch
E(1 − z i )Θi,max
L = 2 ln
(5.134)
mz i
gegeben ist. Für grobe Abschätzungen wird häufig die schon in Abschn. 3.3.2
diskutierte Näherung
L = 2 ln
benutzt.
E
m
(5.135)
337
338
5
Elektronen und Quarks
Um den totalen Wirkungsquerschnitt der Reaktion (5.130) zu erhalten,
muß man (5.131) integrieren. Dazu nimmt man zweckmäßigerweise eine
Variablentransformation vor. Mit der Definition z = ŝ/s und den Beziehungen
z = z1 z2
z1
r=
,
z2
wird (5.131) zu
(5.136)
dσ − +
R
(e e → e− e+ R) = σγγ
(zs)
dz
1/z
√
1
f γ/e ( zr) f γ/e ( z/r) dr
2r
(5.137)
z
umgeformt. Die Argumente |qi2 | der Photondichten f γ/e wurden hier der
Einfachheit halber nicht explizit angegeben. Das Integral
1/z
L γγ (z) =
√
1
f γ/e ( zr) f γ/e ( z/r) dr
2r
(5.138)
z
wird als Luminositätsfunktion bezeichnet. Sie wurde zuerst von Low [Low60]
in der Näherung (5.135) für den Logarithmus berechnet. Das Standardresultat
lautet
α E 2
L γγ =
g(z) ,
(5.139)
ln
π m
worin die Funktion g(z) durch
1
g(z) = (2 + z)2 ln(1/z) − 2(1 − z)(3 + z)
(5.140)
z
definiert ist. Für kleine z-Werte wird g(z) sehr groß. In dieser Region können
wir die Luminositätsfunktion durch
α E 24 1
L γγ =
ln
ln
(5.141)
π m
z z
Luminositätsfunktion
1,8
1,6
1,4
1,2
1
0,8
0,6
0,4
0,2
0
0,01
0,1
z
Abb. 5.27
Die γγ -Luminosität eines e− e+ -Speicherringes als Funktion von z = ŝ/s bei einer
Strahlenergie von E = 20 GeV
approximieren. Wichtig ist die Kompensation des Faktors (α/π)2 für große E
und kleine z in diesem Ausdruck. Auch hier begegnet man wieder der schon
in Abschn. 3.3.2 behandelten effektiven Kopplung αL, die nur schwach von
der Strahlenergie E abhängt. Die Luminositätsfunktion ist in Abb. 5.27 für
eine Strahlenergie von 20 GeV
√ als Funktion von z aufgetragen. Man erkennt
L γγ = 1 bei z ≈ 0,008, d.h. ŝ = 3,6 GeV. Bei dieser Schwerpunktsenergie
wird also die Photon-Photon-Luminosität gleich groß wie die Luminosität des
Speicherrings.
Mit diesen Kenntnissen wollen wir jetzt die Formel für den totalen Wirkungsquerschnitt weiter auswerten. Die verbleibende Integration über z wird
für relativ schmale Resonanzen vereinfacht, da dann L γγ praktisch nur an der
Stelle z R = M 2R /s beiträgt,
− +
− +
R
σ(e e → e e R) = L γγ (z R ) σγγ
(zs) dz .
(5.142)
5
5.4 Zwei-Photonen-Physik
Abb. 5.28
Produktion von f 2 (1270)-Mesonen in der
Photon-Photon-Streuung
σ/nb
γγ
300
π+π –
Mark II
200
100
0
0,3
0,6
0,9
1,2
s/GeV
1,5
Mit Hilfe von (2.261) und (2.263) und der Tatsache, daß das statistische
Gewicht für zwei einlaufende Photonen 1/2 beträgt,14 lautet das über alle
Endzustände summierte Ergebnis für die Produktion eines Mesons mit dem
Spin J und der Zwei-Photonen-Partialbreite Γγγ
8π 2 (2J + 1)Γγγ
.
(5.143)
4E 2 M R
Unter Benutzung der Näherung (5.141) erreichen wir schließlich
(2J + 1)Γγγ 2 E
2E
σ(e− e+ → e− e+ R) = 64α2
ln
,
(5.144)
ln
3
m
M
MR
R
eine v.a. für Zählratenabschätzungen gut brauchbare Formel.
Die γγ -Zerfallsbreite von Mesonen ist selbst wieder proportional zu α2 ,
und damit wird der totale Wirkungsquerschnitt proportional zu α4 . In
Abschn. 4.5.3 hatten wir gesehen, daß diese Zerfallsbreite für viele Mesonen Werte von einigen eV bis zu einigen keV hat. Eine experimentelle
Bestimmung durch Analyse der Zwei-Photonen-Reaktionen an ElektronPositron-Speicherringen ist wegen des Faktors 1/M 3R in (5.144) daher nur
für nicht zu große Massen der Resonanzen sinnvoll. In den letzten Jahren
wurde hier eine Reihe von schönen Ergebnissen erzielt und ein neuer Zweig
der Meson-Spektroskopie begründet. Natürlich darf die Berechnung des Photonenflusses nicht die vielen Näherungen der Beziehung (5.144) benutzen.
Eine Integration von (5.131) ist aber mit numerischen Methoden gut möglich.
Die Abb. 5.28 zeigt die Rekonstruktion von in Zwei-Photonen-Reaktionen
erzeugten f 2 -Mesonen in ihrem dominanten Zwei-Pionen-Zerfallskanal
über einem nicht resonanten Untergrund. Die Experimente ergeben einen
Wert von Γγγ = 2,45 ± 0,31 keV, der gut mit Quarkmodell-Rechnungen
übereinstimmt [Ber87a].
σ(e− e+ → e− e+ R) = L γγ (z R )
14
Der Gewichtungsfaktor 1/4 der Spins muß
mit 2 multipliziert werden, da Γγγ für zwei
auslaufende Photonen berechnet wird und daher einen Faktor 1/2 als Gewicht für zwei
identische Teilchen im Endzustand enthält.
339
340
5
Elektronen und Quarks
5.4.2 Die Strukturfunktion des Photons
Die Berechnung des Wirkungsquerschnitts für die Paarerzeugung von Myonen
(Abb. 5.26b) in der Reaktion
e− + e+ → e− + e+ + µ− + µ+
e
e
q
q
e
e
Abb. 5.29
Feynman-Diagramm der Hadron-Produktion in der Elektron-Photon-Streuung
(5.145)
birgt in der Näherung, daß beide Photonen beinahe auf der Massenschale sind,
(q12 , q22 ≈ 0) keine große Schwierigkeiten. Man muß offenbar entsprechend
zum Vorgehen im letzten Abschnitt zwei Flußfaktoren f 1 und f 2 mit dem in
Abschn. 3.2.5 angegebenen Querschnitt für die Myon-Paarerzeugung durch
reelle Photonen falten. Dies wollen wir hier nicht weiter verfolgen, sondern
uns einer interessanteren kinematischen Situation zuwenden.
Wir betrachten eine Versuchsanordnung, in der nur eines der beiden Photonen, sagen wir das vom Positron abgestrahlte, quasireell ist, während das
andere beliebige virtuelle Massen annehmen kann. Experimentell wird dies erreicht, indem die Streuwinkel für das Positron möglichst klein gehalten werden
(typisch < 3◦ ), das gestreute Elektron jedoch im gesamten Raumwinkelbereich untersucht wird. Der zugehörige Wirkungsquerschnitt läßt sich offenbar
aus einer Multiplikation des Photonenspektrums f e/γ mit dem inelastischen
Elektron-Photon-Streuquerschnitt bestimmen,
dσ(e− e+ → e− e+ X) = dσ(e− γ → e− X) f e/γ (z 2 , Θ2 ) dz 2 .
(5.146)
Das Symbol X steht zunächst für ein Myonpaar. Wir ersetzen aber die Myonen
sofort durch Quarks und nehmen wie früher an, daß die Quarks in einen beliebigen Endzustand X fragmentieren. Die Formel (5.146) beschreibt dann die
Hadronproduktion in Zwei-Photonen-Reaktionen, wobei eines der Photonen
eine große virtuelle Masse besitzt (Abb. 5.29).
Den Wirkungsquerschnitt für die inelastische Elektronen-Streuung, eγ →
eX, können wir direkt aus (5.67) übernehmen, wenn wir in Gedanken das
einlaufende Proton durch ein einlaufendes Photon ersetzen. Das Resultat lautet
d2 σ eγ
4πα2 γ
2 γ
+
xy
F
.
(5.147)
=
(1
−
y)F
2
1
dq 2 dx
q4 x
Die Variablen x und y lassen sich aus den Definitionen (5.59) und (5.57)
unmittelbar für den Fall der Elektron-Photon-Streuung auswerten (wobei P
jetzt den Viererimpuls des kollinear mit dem Positron abgestrahlten reellen
Photons bezeichnet),
x=
−q 2
W 2 − q2
(5.148)
und
E 1
cos2 (Θ1 /2) .
(5.149)
E
In der letzten Gleichung sind E 1 und Θ1 Energie und Winkel des auslaufenden
Elektrons. Die Strukturfunktion ist wiederum durch die Zahl der Quarks mit
dem Bruchteil x des Photon-Impulses definiert. Im Gegensatz zur NukleonStrukturfunktion werden bei der Summation die Antiquarks aber nicht als
y = 1−
5
5.4 Zwei-Photonen-Physik
eine eigene Sorte gezählt, und somit gilt für den Zusammenhang mit der
Verteilungsfunktion f q/γ
γ
F2 (x, q 2 ) = 2x
3Q 2f f q/γ (x, q 2 ) .
(5.150)
f
Der Faktor 3 in der Summe kommt von den drei Farbfreiheitsgraden, damit
wird f q/γ (x, q 2 ) dx die Zahl der Quarks einer bestimmten Farbe und einer
bestimmten Sorte mit Impulsbruchteilen zwischen x und x + dx.
Der Leser, der der Diskussion bis hierhin gefolgt ist, wird sich vielleicht
fragen, wieso das Photon als elementares Feldteilchen jetzt eine Strukturfunktion bekommt, die bisher nur für zusammengesetzte Teilchen definiert war.
Der Name ist nur durch die formale Ähnlichkeit der Streuformeln begründet.
Die Funktion f q/γ beschreibt nicht einen wirklichen Quarkinhalt, sondern die
Wechselwirkung des Photons mit den elektrisch geladenen Quarks und ist
ähnlich wie die mit ihr eng verwandte Funktion f γ/e in der QED berechenbar.
Vertiefung
Eine Analyse der Berechnung von f γ/e in der QED zeigt, daß die in
Abschn. 3.3.1a eingeführte Splitting-Funktion P eγ proportional zu |T fi2 |
für den Übergang e → eγ wird, wobei |T fi2 | einen Faktor
E 2 + E 2
(5.151)
ω
enthält. E, E und ω sind die Energien des ein- und auslaufenden Elektrons
bzw. des Photons in einem Bezugsystem hoher Impulse für das einlaufende
Elektron. Mit z = ω/E wird die angegebene Abhängigkeit der SplittingFunktion P eγ vom Impulsbruchteil z verständlich. Die Splitting-Funktion
P γe ist mit P eγ über eine crossing-Relation verwandt, da der Prozeß γ →
e− e+ mit dem Prozeß e → eγ durch Vertauschen des Photons mit dem
Elektron verknüpft ist. Dies bedeutet die Ersetzung E ↔ ω in (5.151) und
daher erhält man
P γe = z 2 + (1 − z)2 .
(5.152)
Diese Splitting-Funktion ist ersichtlich symmetrisch in den Impulsbruchteilen der auslaufenden Elektronen und Positronen. Es fällt außerdem auf,
daß sie keine Divergenz aufweist. Genau wie bei der Berechnung von f γ/e
in Abschn. 3.3.1a müssen wir noch den Logarithmus des Verhältnisses des
maximalen und minimalen Impulsübertrages bestimmen. Diese Analyse
führt dann zum Resultat
α γe |k2 |max (1 − z)
P ln
(5.153)
2π
m2z
für die spektrale Verteilung der Elektronen und Positronen in einem Photon.
f e/γ =
341
342
5
Elektronen und Quarks
Das Ergebnis, dessen Herleitung im Kasten erläutert ist, lautet
q 2 (x − 1)
α 2
f q/γ (x, q 2 ) = Q 2f
x + (1 − x)2 ln
,
2π
m q2 x
(5.154)
wobei die Bezeichnung der Variablen des Impulsbruchteils der betrachteten
Situation angepaßt wurde. Außerdem wurde ein Faktor Q 2f für die Ladung der
Quarks eingefügt. Der maximale Impulsübertrag bei der Aufspaltung des reellen Photons in ein Quark-Antiquark-Paar ist durch |k2 |max = |q 2 | festgelegt.
In dieser Näherung gilt demnach für die Photonstrukturfunktion
q 2 (x − 1)
α γ
F2 (x, q 2 ) = 3
Q 4f x x 2 + (1 − x)2 ln
.
(5.155)
π
m q2 x
f
Wie in der Elektron-Proton-Streuung wird die eγ -Streuung durch zwei Strukγ
γ
γ
turfunktionen F1 und F2 bestimmt. Auch F1 läßt sich in der QED berechnen.
Da die meisten Experimente jedoch bei kleinem y durchgeführt werden,
γ
kann man den Term mit F1 in (5.147) i.allg. vernachlässigen. Das Resultat (5.155) hat einige sehr bemerkenswerte Eigenschaften. Zunächst einmal
hängt die Strukturfunktion explizit von q 2 ab, zeigt also auch ohne QCDKorrekturen kein Skalenverhalten. Weiterhin steigt sie zu großen Werten
von x an (Abb. 5.30), im Gegensatz zu hadronischen Strukturfunktionen.
Beide Eigenschaften sind eine unmittelbare Folge der Tatsache, daß schon
in niedrigster Ordnung der Störungstheorie die Strukturfunktion proportional
zu f q/γ wird, während f g/q in den hadronischen Strukturfunktionen nur als
Korrekturterm auftritt.
Das Quarkmodell-Resultat (5.155) hat den entscheidenden Nachteil, daß es
explizit von den Quarkmassen abhängt, die aber für eingeschlossene Quarks
nicht wohldefiniert sind. Von der Natur der Herleitung ausgehend, ist es
naheliegend, die Konstituentenmassen, also etwa 300 MeV für die leichtesten Quarks, einzusetzen. In einer grundlegenden Analyse hat E. Witten
gezeigt [Wit77], daß die QCD-Korrekturen (5.155) bei sehr großen Werten
von |q 2 | in
γ
F2 (x, q 2 ) = h(x) ln
|q 2 |
Λ2
(5.156)
abändern, wobei h(x) eine berechenbare Funktion ist, die – wie im Quarkmodell – mit x ansteigt. Der wesentliche Inhalt der Beziehung (5.155), nämlich
die logarithmische Abhängigkeit von q 2 und der Anstieg von F2 mit großen x,
bleibt also auch in der QCD-Rechnung, d.h. unter Berücksichtigung einer
zusätzlichen Gluonabstrahlung von den Quarks, erhalten. Die Quarkmassen
werden durch den QCD-Parameter Λ ersetzt. Eine detaillierte Betrachtung
dieser interessanten Fragen kann der Leser in der Literatur [Ber87a] finden.
In Abschn. 4.5.1 wurde ein hadronisches Modell der Photon-Hadron-Wechselwirkung, die Vektor-Meson-Dominanz, diskutiert. Da ein hochenergetisches reelles Photon z.B. in ein ρ-Meson fluktuieren kann, erwarten wir in
den Meßergebnissen eine harte punktförmige Komponente gemäß (5.155) und
eine weiche hadronische Komponente, die zu großen x hin abfällt und typisch
5
F2 /α
5.4 Zwei-Photonen-Physik
PLUTO
Strukturfunktionen des Photons
bei 3 Werten von |q 2|
1,0
Abb. 5.30
γ
Eine Messung von F2 als Funktion von x
2
und |q | [Ber87b]
Punkte: Meßwerte nach Abzug
des charm-Beitrags
Kurve: QCD fit
(Λ = 183 MeV)
0,9
0,8
0,7
0,6
|q 2| = 45,0 GeV 2
0,5
0,4
0,3
0,5
0,4
|q 2| = 9,2 GeV 2
0,3
0,2
0,4
0,3
|q 2| = 4,3 GeV 2
0,2
0,1
0
0,25
0,50
0,75
x
1,00
für das Verhalten hadronischer Strukturfunktionen ist. Experimentell konnten in der Tat beide Komponenten isoliert werden. Für große Werte von |q 2 |
wird der punktförmige Anteil dominant. Die Abb. 5.30 zeigt das Ergebnis eines mit dem PLUTO-Detektor im DESY durchgeführten Experiments.15 Die
γ
Kurven entsprechen den theoretischen Vorhersagen der QCD für F2 .
Übung
5.8
15 Die
Schätzen sie die Erzeugungsraten von π -, η- und η -Mesonen in
Zwei-Photonen-Reaktionen am Speicherring PETRA (Strahlenergie
15 GeV) ab.
0
großen experimentellen Arbeitsgruppen
der Teilchenphysik sind meist nur noch durch
den Namen des Detektors bekannt. Der Name
PLUTO stammt aus einer Zeit, als bei DESY
noch alle großen Magnete nach Gestalten der
antiken Mythologie benannt wurden.
343
http://www.springer.com/978-3-540-41515-2

Zugehörige Unterlagen

Arbeitsblatt: Im Inneren des Kerns

Feynman-Diagramme

Vorwort - Springer

Zugehörige Unterlagen

Produkte

Unterstützung

Vorwort - Springer

Zugehörige Unterlagen

Dieses Dokument Sammlung (en)

Dieses Dokument gespeichert

Schlagen Sie uns vor, wie wir StudyLib verbessern können