Vorlesung 1 - PH Heidelberg

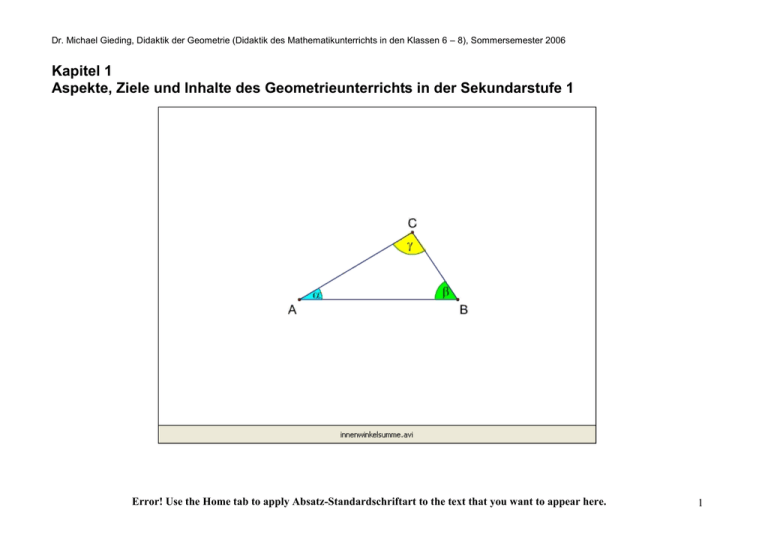
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
Kapitel 1
Aspekte, Ziele und Inhalte des Geometrieunterrichts in der Sekundarstufe 1
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
1
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
Aspekte der Vermittlung von Elementen der Geometrie im Mathematikunterricht der SI
Geometrie?
Wortherkunft
Das Wort Geometrie kommt aus dem Griechischen:
εωμετρία
Geometria
ge
metrein
Erde
messen
Erdmessung, Erdvermessung
Aufgabe 0: Welche Bedeutung hat die obige Inschrift?
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
2
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
Arten von Geometrien1
a) Synthetische vs. analytische Geometrie
Synthetische Geometrie
Analytische Geometrie
6
C
AB: y = 1,50x-4,00
4
B
2
A
xB = 4,00
yB = 2,00
A
5
xA = 2,00
-2
yA = -1,00
-4
B
-6
Beschreibung von Geraden
undefinierter Grundbegriff
Geradengleichung: ax + by + c =0,
rechter Winkel, Relation „senkrecht“
Ein Winkel, der zu einem seiner Nebenwinkel kongruent ist, heißt ein
rechter Winkel.
Zwei sich schneidende Geraden stehen senkrecht aufeinander (bilden
rechte Winkel), wenn das Skalarprodukt zwischen den
Richtungsvektoren der beiden Geraden verschwindet.
Verwendung in der Schule
„Die“ Geometrie in der SI
Randerscheinung in der SI. In SII in starkem Maße unter dem Aspekt der
linearen Agebra.
Aufgabe 1: Beispiel für Elemente der analytischen Geometrie in der SI. Aufgabe 2: Möglichkeit der Definition des Begriffs Parabel.
1
Es ist an dieser Stelle nicht möglich, auf alle existierenden Geometrien einzugehen. Wir beschränken uns auf Aspekte der Geometrie, die einen mehr oder weniger deutlichen
Bezug zur Schulgeometrie haben.
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
3
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
b) Euklidische vs. nichteuklidische Geometrie
Euklidische Geometrie
Nichteuklidische Geometrien
Satz über die Innenwinkelsumme im Dreieck:
Beispiel: Sphärische Geometrie
C
A



B
Beschriften Sie das obige Dreieck (Seiten Winkel) entsprechend
der im Schulunterricht gültigen Konventionen!
Zeichnen Sie die Außenwinkel ein und beschriften Sie diese!
Formulieren Sie den Innenwinkel- und einen Außenwinkelsatz
für Dreiecke!



Auf der obigen Kugel wurden 8 zueinander kongruente
(sphärische) Dreiecke konstruiert. Kennzeichnen Sie für eines
dieser Dreiecke die Innenwinkel ein.
Wie groß ist die Innenwinkelsumme für jedes dieser Dreiecke?
Gilt der aus der Schule bekannte Außenwinkelsatz?
Diese Aufgabenstellung für Classroompresenter laden
Unter Geometrie versteht man auf der SI euklidische Geometrie.
Ehemals klassischer Schulstoff an Gymnasien
Eine genauere Erläuterung des Begriffs Euklidische Geometrie erfolgt an späterer Stelle.
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
4
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
c) Darstellende Geometrie
 Große Tradition in Österreich (kann als eigenständiges Fachstudiert werden).
 An den Haupt- und Realschulen Baden-Württembergs eher unterrepräsentiert.
 Lediglich „Schrägbilder“
 Der Begriff „Schrägbild“ wird synonym zur Darstellung eines dreidimensionalen Objekts in Kavalierperspektive verwendet.
Die folgende Abbildung soll einen Würfel darstellen. Warum handelt es dabei um kein echtes „Schrägbild“ eines Würfels?
H
G
F
E
C
D
A
B
Diese Aufgabestellung für Classroompresenter laden
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
5
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
d) Kegelschnitte
Generierung der Grafik: Prof. Dr. Filler mit Pov-Ray
ehemals klassischer Stoff an Gymnasien (SII)
weiterführende Lieteratur: Schupp, Hans: Kegelschnitte, Franzbecker, 2000
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
6
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
e) Elemente der Geometrie die durch die Entwicklung moderner digitaler Medien für die Schulgeometrie an Bedeutung gewinnen könnten:
 Dynamische Geometriesoftware: Unterstützung der Leitidee „funktionaler Zusammenhang“ im Geometrieunterricht:
G

H

E
F
Animate Point

Bildschirme und Drucker setzten ihre Darstellungen aus einzelnen Punkten zusammen: diskrete Geometrie

2- und 3D-Computergrafik
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
7
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
Problem Geometrieunterricht
„Haben wir heute Geometrie oder Mathematik?“
Schülerfrage
Ein Beispiel: Satz über die Innenwinkelsumme im Dreieck
a) Beliebtes Vorgehen:
C



A

C
 

B
„Abreißen der Winkel“
A


B
„An C anlegen“
Offenbar gilt: =180°
Kommentieren Sie stichpunktartig Sinn und Zweck dieser enaktiven Übung!
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
8
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
b) Andere Möglichkeit: Jeder Schüler konstruiert ein beliebiges Dreieck und mißt die Innenwinkel
<CAB = 56
<ABC = 43
C
<BCA = 82
Animate Points
<CAB +<ABC +<BCA  = 180,00
A
B
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
9
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
c) Ein Beweis:
C



A
B
Aufgabe für Classroompresenter laden.
Behauptung: 
Beweisschritt
Begründung
C
p



A
B
Konstruieren p, die Parallele durch C zu AB
C
'

'

p

A
B
Es entstehen die Winkel ’ und ’.
’, ’

d) Problem des Beweises
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
10
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006


Der Beweis des Satze beruht auf dem Satz über Wechselwinkel an geschnittenen Parallelen.
Dieser läßt sich nur beweisen, wenn von folgender Aussage ausgegangen werden darf:
Euklidisches Parallelenaxiom:
Es seien g eine Gerade und P ein nicht auf g liegender Punkt. Dann existiert genau eine Gerade, die p, die durch P geht und zu g
parallel ist.
 Das Euklidische Parallelenaxiom läßt sich nicht beweisen.
 Es wird als unbeweisbare Tatsache vorausgesetzt.
 Eine Geometrie, die auf dem Euklidischen Parallelenaxiom aufbaut, heißt Euklidische Geometrie.
 Es gibt Geometrien, die etwa auf dem folgenden Parallelenaxiom aufbauen:
Parallelenaxiom von Lobatschewski:
Es existiert mindestens eine Gerade g und ein nicht auf g liegender Punkt P, durch den mindestens zwei Geraden verlaufen, die g
nicht schneiden.
 In der Lobatschewski-Geometrie lautet der Innenwinkelsatz für Dreiecke wie folgt:
Die Innenwinkelsumme eines jeden Dreiecks ist kleiner als zwei Rechte.
e) Das eigentliche Problem für die Schulgeometrie:
 Geometrie auf der SI ist Euklidische Geometrie, Der Satz über die Innenwinkelsumme von Dreiecken diente hier zur Verdeutlichung
des Problems, worauf man sich bei Beweisen berufen darf.
 In der Schulgeometrie bleibt dem Schüler (und häufig auch dem Lehrer) verborgen, worauf er sich berufen darf.
 Der Mathematiker lößt das Problem durch die Angabe eines Axiomensystems.
 Würde axiomatische Geometrie das schulische Problem lösen?
Literatur:
Filler, Andreas: Euklidische und Nichteuklidische Geometrie
Schupp, Hans: Figuren und Abbildungen
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
11
Dr. Michael Gieding, Didaktik der Geometrie (Didaktik des Mathematikunterrichts in den Klassen 6 – 8), Sommersemester 2006
Axiomatik für die Schulgeometrie?
Error! Use the Home tab to apply Absatz-Standardschriftart to the text that you want to appear here.
12