Analysis T1, Analysis 1b WS 2015/2016 5. Übungsblatt 18. Lösen

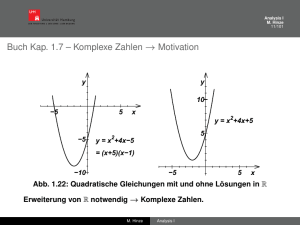
Analysis T1, Analysis 1b
WS 2015/2016
5. Übungsblatt
18. Lösen Sie folgende Gleichungen über den komplexen Zahlen. Geben Sie jeweils Realund Imaginärteil der Lösung an.
(a)
(1 + 2i)z + 9
= 8 − 5i,
(3 + 4i)z − (9 + 4i)
(b) z 2 = 3 − 4i,
(c) z 2 − 7z + (13 − i) = 0,
19. Zeigen Sie: Sind die Realteile von z, w ∈ C beide positiv oder beide negativ, so gilt die
Ungleichung
|z − w|
< 1.
|z + w̄|
20. (a) Es sei c ∈ C mit Im c ≥ 0 (< 0) gegeben. Zeigen Sie, dass
r
r
1
1
+
z :=
(|c| + Re c)
(|c| − Re c)
i
(−)
2
2
eine Quadratwurzel von c ist, d. h. z 2 = c.
(b) Jedes c ∈ C, c 6= 0, besitzt genau zwei Quadratwurzeln z1 , z2 ∈ C mit z2 = −z1 .
21. Überprüfen Sie die folgenden Reihen auf Konvergenz
(a)
(b)
(c)
∞ n
X
i
n=1
∞
X
n=1
∞
X
n
(1 + i)n
n3
(3 − 5i)n
.
n!
n=0