ω ω ω ω ε ω ε

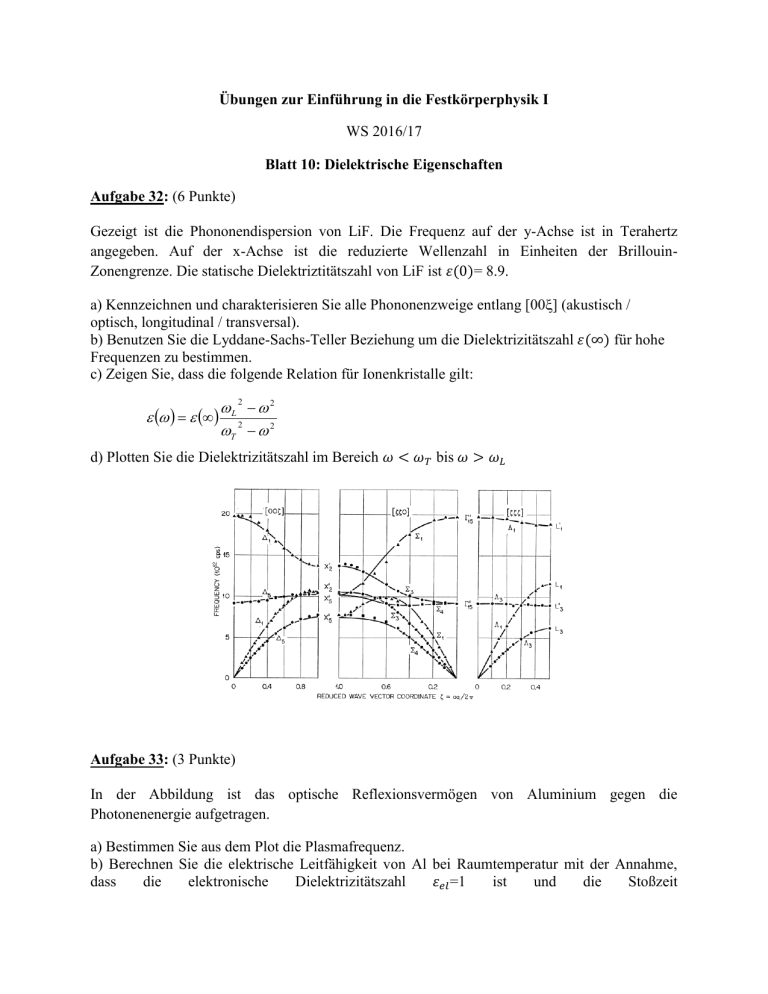
Übungen zur Einführung in die Festkörperphysik I
WS 2016/17
Blatt 10: Dielektrische Eigenschaften
Aufgabe 32: (6 Punkte)
Gezeigt ist die Phononendispersion von LiF. Die Frequenz auf der y-Achse ist in Terahertz
angegeben. Auf der x-Achse ist die reduzierte Wellenzahl in Einheiten der BrillouinZonengrenze. Die statische Dielektriztitätszahl von LiF ist 𝜀(0)= 8.9.
a) Kennzeichnen und charakterisieren Sie alle Phononenzweige entlang [00] (akustisch /
optisch, longitudinal / transversal).
b) Benutzen Sie die Lyddane-Sachs-Teller Beziehung um die Dielektrizitätszahl 𝜀(∞) für hohe
Frequenzen zu bestimmen.
c) Zeigen Sie, dass die folgende Relation für Ionenkristalle gilt:
L 2   2
       2
T   2
d) Plotten Sie die Dielektrizitätszahl im Bereich 𝜔 < 𝜔 𝑇 bis 𝜔 > 𝜔𝐿
Aufgabe 33: (3 Punkte)
In der Abbildung ist das optische Reflexionsvermögen von Aluminium gegen die
Photonenenergie aufgetragen.
a) Bestimmen Sie aus dem Plot die Plasmafrequenz.
b) Berechnen Sie die elektrische Leitfähigkeit von Al bei Raumtemperatur mit der Annahme,
dass
die
elektronische
Dielektrizitätszahl
𝜀𝑒𝑙 =1
ist
und
die
Stoßzeit
7x10-13 s beträgt. Vergleichen Sie die aus der Plasmafrequenz ermittelte Leitfähigkeit mit der
tatsächlich bei Raumtemperatur gemessen Leitfähigkeit von 𝜎𝑒𝑥𝑝 = 6,5 x 107 (m)-1
c) Zeichnen Sie qualitativ den Reflexionskoeffizient von elektromagnetischen Wellen als
Funktion der Frequenz, wenn Sie kein Metall (wie in (a) & (b)), sondern ein Ionenkristall haben.
Aufgabe 34: (6 Punkte)
Wird ein ellipsoidförmiger dielektrischer Festkörper in ein homogenes elektrisches Feld 𝐸⃗𝑒𝑥𝑡
gebracht, so wird dieser homogen polarisiert. Wir erhalten dann im Innern des Festkörpers ein
−𝑁𝑃⃗
makroskopisches elektrisches Feld der Stärke 𝐸⃗𝑚𝑎𝑘 = 𝐸⃗𝑒𝑥𝑡 + 𝐸⃗𝑁 , wobei 𝐸⃗𝑁 =
das
𝜀0
Entelektrisierungsfeld ist. Die Größe N ist dabei der Entelektrisierungsfaktor der Probe, der im
allgemeinsten Fall einen Tensor 2. Stufe darstellt, und 𝑃⃗ die in der Probe vorliegende homogene
Polarisation.
a) Zwischen den Hauptkomponenten des Entelektrisierungstensors besteht die Beziehung
𝑁𝑥𝑥 + 𝑁𝑦𝑦 + 𝑁𝑧𝑧 = 1. Welche Werte müssen die Hauptkomponenten für eine Kugel, einen
unendlich langen Stab, und eine unendlich ausgedehnte dünne Scheibe annehmen?
b) Leiten Sie einen Ausdruck für das in der Probe herrschende makroskopische elektrische Feld
𝐸⃗𝑚𝑎𝑘 her.
c) Welcher Zusammenhang besteht in diesem Fall zwischen
⃗ und dem extern angelegten elektrischen Feld 𝐸⃗𝑒𝑥𝑡 ?
Verschiebungsdichte 𝐷
der
dielektrischen
d) Berechnen Sie das Verhältnis 𝐸𝑚𝑎𝑘 ⁄𝐸𝑒𝑥𝑡 für einen Festkörper mit einer
Dielektrizitätskonstante von 𝜀= 2.5, wenn dieser die Form eines langen Stabes, einer Kugel oder
einer dünnen Scheibe besitzt. Das externe elektrische Feld soll dabei parallel zum Stab bzw.
senkrecht zur Scheibe angelegt sein.