Lösungen zu Übung (2)

Lösungen zu Übung (2)
1. (a) Anders als bei Aufgabe 3 vom ersten Blatt ist hier nach ’a’ als oberster Karte kein weiterer Buchstabe a
zu ziehen, usw. (Es ist derselbe Unterschied wie ’Ziehen mit Zurücklegen’ - so Aufg. 3 vom ersten Blatt und hier ’Ziehen ohne Zurücklegen’. Wir haben hier:
Ω = {(x1 , x2 , x3 , x4 ) |für alle i mit 1 ≤ i ≤ 4: xi ∈ {a, b, c, d, h} und xi = xj für i = j, 1 ≤ i, j ≤ 4. }
Entsprechend hat man
|Ω| = 5 · 4 · 3 · 2 = 5! = 120.
Dass es sich um einen Laplaceraum handelt, steht im Text mit ’Karten gemischt und oben gezogen’, es
entsteht also eine Zufallspermutation. Daher kommt das Wort ’dach’ mit Wahrscheinlichkeit 1/120.(Der
fehlende Buchstabe b muss unten liegen!)
(b) Antwort mit der ersten Strategie: Es könnte d1 ad2 a heißen oder auch d2 ad1 a, ebenso könnten die beiden
a− Karten vertauscht werden, also hat man unter den 120 Fällen (aus Aufgabenteil a) vier ’günstige’, und
so ist die Wahrscheinlichkeit für das Wort ’dada’:
P ({(d, a, d, a)}) =
4
1
= .
120
30
2
. Wenn die
5
oberste Karte eine d− Karte war, so ist die (dadurch bedingte) Wahrscheinlichkeit dafür, eine a− Karte zu
2
1
ziehen, = . So machen wir weiter und erhalten mit der ’Pfadregel’:
4
2
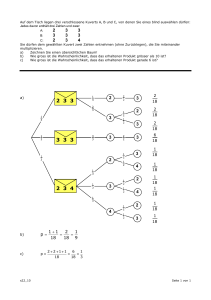
Antwort mit der zweiten Strategie: Zuerst wird eine d− Karte gezogen mit Wahrscheinlichkeit
P ({(d, a, d, a)}) =
2 1 1 1
1
· · · = .
5 2 3 2
30
(Wir stellen fest, dass der erste Weg eleganter war, aber der zweite hat den Vorteil, das ’Ziehen ohne
Zurücklegen genau zu illustrieren.)
2. Man hat A = {2, 4, 6} , B = {2, 3, 5} , Wir zählen die geraden Zahlen im verkleinerten Topf B, bekommen
einen von drei gleichwahrscheinlichen Fällen, also P (A|B) = 1/3. Da dies = P (A) = 1/2 ist, sind A, B abhängig
(gemäß der Charakterisierung der Unabhängigkeit des Paars A, B mit P (B) = 0 durch die Bedingung P (A|B) =
P (A)). Zweiter Weg zu diesem Ziel: P (A) P (B) = 1/4, aber P (A ∩ B) = P ({2}) = 1/3.
3. Es bestehe eine Bevölkerung Ω von Menschen im Erwerbstätigenalter aus zwei disjunkten Teilpopulationen B, C.
(Also B ∪ C = Ω und B ∩ C = ∅.) B mache 30% von Ω aus. In B seien 3% arbeitslos, in C seien es 10%.
(a) Die Angaben sind: P (B) = 3/10, woraus folgt: P (C) = 7/10. Weiter P (A|B) = 3/100, P (A|C) = 1/10.
(b) Nach der Formel für die totale Wahrscheinlichkeit (für den einfachen Fall von nur zwei Klassen) hat man
P (A) = P (A|B) P (B) + P (A|C) P (C) =
3
3
1 7
79
·
+
·
=
= 0.079 (exakte Dezimalzahl!).
100 10 10 10
1000
Nun wird man als Resultat in Prozent mitteilen: Es sind etwa 8% Arbeitslose in der Gesamtbevölkerung.
(c) Man sollte sofort intuitiv sehen, dass die Arbeitslosen in C überrepräsentiert sind und daher A, C ein
abhängiges Paar bildet. Aber man kann natürlich auch sagen: P (A) = 0.079 = 0.1 = P (A|C) , mit
derselben Konsequenz.
4. (a) Laut Text hat man:
P (KT |K) = 0.98 = P KT |K ,
P KT |K = 0.02 = P KT |K .
1
(b) Gefragt ist nach P (K|KT ) . Es geht also um das Herumdrehen der Bedingungsrichtung. Dafür ist die
Bayessche Formel zuständig, auf diesen Fall angewandt:
P (K|KT ) =
P (KT |K) P (K)
P (KT |K) P (K)
.
=
P (KT )
P (KT |K) P (K) + P KT |K P K
Das heißt für
i. (wenn 1/3 der Gesamtbevölkerung die Krankheit hat) - Kürzen(!):
0.98 · 1/3
0.98 · 1/3 + 0.02 · 2/3
0.98
=
≈ 0.96.
0.98 + 0.04
ii. (wenn 1/100 der Gesamtbevölkerung die Krankheit hat):
P (K|KT ) =
P (K|KT ) =
=
0.98 · 1/100
0.98 · 1/100 + 0.02 · 99/100
0.98
≈ 0.33.
0.98 + 1.98
5. Es sei (Ω, S, P ) ein beliebiger Wahrscheinlichkeitsraum.
(a) Dann hat man für alle A, B ∈ S: Wenn P (A) P (B) = P (A ∩ B) (∗), dann
P (A) P B = P (A) (1 − P (B)) = P (A) − P (A) P (B)
=
=
mit (∗)
∗∗
P (A) − P (A ∩ B)
P A∩B .
Das letzte Gleichheitszeichen (∗∗) hat man mit:
P (A) = P (A ∩ B) + P A ∩ B ,
was wir schon kennen.
(b) In die Aussageform ’A, B unabhängig =⇒ A, B unabhängig’ dürfen wir gemäß der in a gezeigten Allaussage
einsetzen: B für A und A für B, es entsteht:
B, A unabhängig =⇒ B, A unabhängig.
Da Unabhängigkeit eine symmetrische Relation ist, folgt die erste Behauptung. Die zweite folgt mit der
Einsetzung: A für A, in dieselbe Aussageform. Das ergibt: A, B unabhängig =⇒ A, B unabhängig. Nun
haben wir
A, B unabhängig
A, B unabhängig
=⇒
=⇒
A, B unabhängig, und
A, B unabhängig.
Das ergibt zusammen
A, B unabhängig =⇒ A, B unabhängig.
Bemerkungen: Es liegen folgende Erweiterungen für die Übung nahe, für den Fall, dass dies alles recht glatt ging:
1.) Variation der Zahl der Karten (Buchstaben) in 1.a., ebenso wie der Buchstabenwiederholungen auf den Karten
in 1.b,
2.) Anlässlich des Beispiels der Abhängigkeit in Aufgabe 2: (i) Betonung der Tatsache, dass P (A|B) keinerlei
zeitlicher Nacheinander des Eintretens von B,A bedeutet, anders als in Beispielen wie ’1. Wurf 1’ und ’Augensumme
von 1. und 2. Wurf ist höchstens 4’. (An diesem könnte man die direkte Bestimmung der bedingten Wahrscheinlichkeit
noch einmal üben - und die Reihenfolge der Bedingtheit auch sogar umdrehen!) (ii) Betonung der Tatsache, dass
wahrscheinlichkeitstheoretische Abhängigkeit nichts mit ’Ursachen’ zu tun hat.
3.) Verallgemeinerung von Aufgabe 3 für typische Anwendungsfälle wie: Es liegen prozentuale Häufigkeiten eines
Merkmals für die einzelnen Bundesländer vor - wie maacht man daraus die für die ganze Republik?
4.) Diskussion der Frage, ob man die verschiedenen Ergebnisse in Aufgabe 4b (i) ,(ii) noch extremer gestalten
könnte - und eben gerade durch den Anteil der ’Kranken’ an der gesamten Bevölkerung.
2