KLAUSUR SPIELTHEORIE

Prof. Ana B. Ania
Wintersemester 2008/09
KLAUSUR SPIELTHEORIE
Aufgabe 1. [15 Punkte] Berechnen Sie alle Nash Gleichgewichte im folgenden Spiel.
T
Spieler 1 M
B
L
2, 0
3, 4
1, 3
Spieler 2
C
R
1, 1
4, 2
1, 2
2, 3
0, 2
3, 0
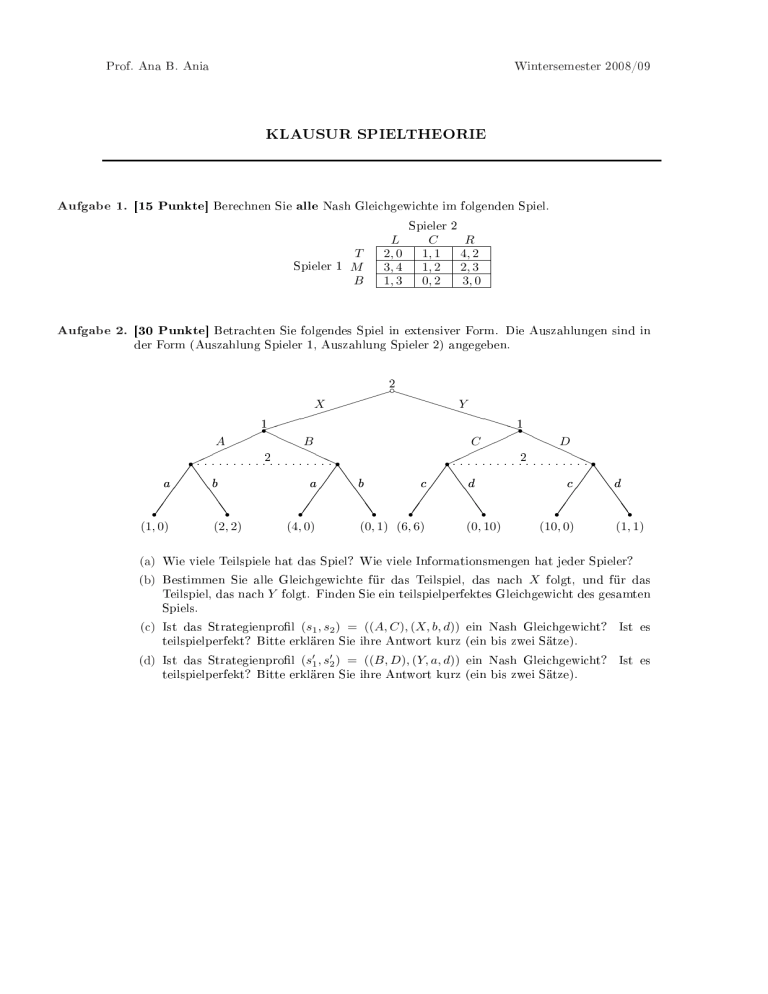
Aufgabe 2. [30 Punkte] Betrachten Sie folgendes Spiel in extensiver Form. Die Auszahlungen sind in
der Form (Auszahlung Spieler 1, Auszahlung Spieler 2) angegeben.
2
³ bPP
³
³³
X
³³
³³
PP Y
PP
PP
PP1r
1r³³
©H
©H
©
H
©
HH D
A©
B
C©
H
©
H
©
H
r p©
©
pr p©
p p p p p p p p p2 p p p p p p pHp H
p pr
p©
p p p p p p p p p2 p p p p p p pHp H
p pr
­J
­J
­J
­J
c­ Jd
c­ Jd
a­ Jb
a­ Jb
J
­
J
­
J
­
J
­
JJr
­
J
­
J
­
J
­
r­
r­
Jr
r
Jr
­
r
Jr
­
(10, 0)
(1, 1)
(0, 10)
(4, 0)
(0, 1) (6, 6)
(1, 0)
(2, 2)
(a) Wie viele Teilspiele hat das Spiel? Wie viele Informationsmengen hat jeder Spieler?
(b) Bestimmen Sie alle Gleichgewichte für das Teilspiel, das nach X folgt, und für das
Teilspiel, das nach Y folgt. Finden Sie ein teilspielperfektes Gleichgewicht des gesamten
Spiels.
(c) Ist das Strategienprol (s1 , s2 ) = ((A, C), (X, b, d)) ein Nash Gleichgewicht? Ist es
teilspielperfekt? Bitte erklären Sie ihre Antwort kurz (ein bis zwei Sätze).
(d) Ist das Strategienprol (s01 , s02 ) = ((B, D), (Y, a, d)) ein Nash Gleichgewicht? Ist es
teilspielperfekt? Bitte erklären Sie ihre Antwort kurz (ein bis zwei Sätze).
Prof. Ana B. Ania
Wintersemester 2008/09
Aufgabe 3. [30 Punkte] Betrachten Sie das Spiel
Spieler 1 A
B
Spieler 2
A
B
2, 2
0, 2
0, 6
5, 5
(a) Nehmen Sie an, Spieler 1 wählt A mit Wahrscheinlichkeit p und B mit Wahrscheinlichkeit 1 − p (entsprechend Spieler 2 mit q und 1 − q ). Stellen Sie die Reaktionsfunktionen grasch dar. Beschriften Sie die Achsen mit p und q und die Reaktionsfunktionen
der Spieler.
(b) Bestimmen Sie alle Nash Gleichgewichte dieses Spiels. Sie können dazu das Diagramm
aus (3a) nutzen.
(c) Nehmen Sie an, das Spiel wird zweimal wiederholt. Gibt es teilpielferkte Gleichgewichte
des zweimal wiederholtes Spiel, die mit (B, B) in der ersten Periode anfangen? Begründen Sie kurz Ihre Antwort (ein bis zwei Sätze).
(d) Nehmen Sie jetzt an, das Spiel wird unendlich oft wiederholt und die Spieler diskontieren
ihre Auszahlungen mit 0 < δ < 1. Betrachten Sie die Strategie: Fange mit B an. Spiele
danach B , wenn der Gegner in der Vorperiode B gespielt hat; spiele A, wenn er A gespielt
hat. Kann diese Strategie Auszahlungen (5, 5) in einem Nash Gleichgewicht stützen?
Ermitteln Sie dafür die Bedingung an δ . Wäre es gegebenenfalls ein teilspielperfektes
Gleichgewicht? Begründen Sie bitte Ihre Antwort (ein bis zwei Sätze).
(e) Finden Sie ein teilpielperfektes Gleichgewicht des unendlich oft wiederholten Spiels.
Aufgabe 4. [25 Punkte] Es soll ein einmaliges und unteilbares Gut in Form einer Auktion mit zwei
Bietern verkauft werden. Mit vi wird der wahre Wert des Gutes für Bieter i = 1, 2 bezeichnet;
das ist der Preis, bei dem Bieter i zwischen Kauf und Nichtkauf indierent wäre. Nehmen wir
an, dass nur die beiden Werte vi ∈ {1, 2} jeweils mit Wahrscheinlichkeit 1/2 möglich sind,
und dass die Werte der beiden Bieter unabhängig voneinander verteilt sind. Jeder Bieter
kennt seinen eigenen Wert, nicht aber den des anderen Bieters; die Verteilung der Werte ist
common knowledge. Die Bieter müssen gleichzeitig ihre Gebote bi machen. Nehmen wir an,
dass nur die drei Gebote bi ∈ {0, 1, 2} möglich sind. Das Gut erhält der Bieter mit dem
höchsten Gebot, er zahlt aber nur das zweithöchste Gebot; d. h. für i 6= j bekommt Bieter i
das Gut immer wenn bi > bj , seine Auszahlung ist dann vi − bj , der andere Bieter j bekommt
und zahlt nichts. Beim unentschiedenen Ausgang geht das Gut an jeden Bieter mit derselben
Wahrscheinlichkeit und die erwartete Auszahlung ist dann (vi − bi )/2.
(a) Was sind die Typen, die Aktionen, die reinen Strategien und die Beliefs in diesem Spiel?
Geben Sie auch die Auszahlungsfunktion eines Spielers in Abhängigkeit der Gebote und
Werte an. Denieren Sie (nicht berechnen!) was in diesem Spiel ein Bayesianisches Nash
Gleichgewicht ist.
(b) Überprüfen Sie, ob das symmetrische Strategienprol in dem ein Bieter mit vi = 1
Gebot bi (1) = 0 und ein Bieter mit vi = 2 Gebot bi (2) = 1 macht ein Bayesianisches
Nash Gleichgewicht ist.
(c) Überprüfen Sie, ob das symmetrische Strategienprol in dem ein Bieter mit vi = 1
Gebot bi (1) = 1 und ein Bieter mit vi = 2 Gebot bi (2) = 2 macht ein Bayesianisches
Nash Gleichgewicht ist.
Prof. Ana B. Ania
Wintersemester 2008/09
ZUSATZKLAUSUR SPIELTHEORIE
Aufgabe 1. [25 Punkte] Betrachten Sie das Problem von zwei Tageszeitungen, die in derselben Stadt
im Wettbewerb stehen. Die tägliche Nachfrage nach Zeitung i als Funktion von den Preisen
beider Zeitungen ist
Di (pi , pj ) = ai − pi + bpj ,
i, j = 1, 2, i 6= j.
Nehmen Sie an, a1 > a2 , 0 < b < 2 und die Produktionskosten beider Zeitungen sind Null.
Die Tageszeitungen wählen den Preis, um ihren Gewinn zu maximieren.
(a) Geben Sie eine Interpretation des Parameters b in den Nachfragefunktionen.
(b) Leiten Sie die beste Antwort jeder Zeitung auf den Preis des Konkurrenten her. Wie
ändert sich der optimale Preis einer Zeitung mit dem des Konkurrenten?
(c) Bestimmen Sie das Nash Gleichgewicht dieses Spiels. Ist das Gleichgewicht symmetrisch?
Diskutieren Sie bitte kurz (ein bis zwei Sätze).
Aufgabe 2. [25 Punkte]
Betrachten Sie folgendes
Signalisierungsspiel, wobei die Auszahlungen in der
³
´
Auszahlung Sender
Form Auszahlung Empfänger angegeben sind. Finden Sie alle perfekt Bayesianischen
Gleichgewichte in reinen Strategien.
¡1¢
2
¡2¢
1
¡4¢
2
¡4¢
3
........ o
o ....
tA
........ [µ ]
[µ ] .......
.
L
R
.
........w.................................................w.................................................w......
........
...
.....
.
.
........
.
.
.
.
..
...
...
....... u
u ...
... 1
... 2
...
...w Natur
Empfänger
Empfänger
...
...
... 1
... 2
........ o
o ....
........
...
....
.
........w..................................................w................................................w..........
........
......
.
.
........
.
.
.
L
R
. [1 − µ ]
[1 − µ ]
...
....... u
u ...
tB
L
¡1¢
0
R
L
R
³
0
−1
´
¡6¢
2
³
3
−1
´