Schnellübung Lösungen, Physik 2 Füllen Sie als erstes

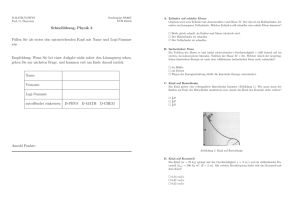
Studienjahr SS2007
ETH Zürich
D-MATH/D-PHYS
Prof. G. Dissertori
Schnellübung Lösungen, Physik 2
Füllen Sie als erstes den untenstehenden Kopf mit Name und Legi-Nummer
aus.
Wenn Sie bei einer Aufgabe nicht sofort den Lösungsweg sehen, gehen Sie
bitte zur nächsten Frage, und kommen erst am Ende darauf zurück.
A. Zylinder auf schiefer Ebene
Gegeben seien zwei Zylinder mit Aussenradius r und Masse M . Der eine sei ein Hohlzylinder, der
andere ein homogener Vollzylinder. Welcher Zylinder rollt schneller eine schiefe Ebene hinunter?
Beide gleich schnell, da Radius und Masse identisch sind.
Der Hohlzylinder ist schneller.
⊠ Der Vollzylinder ist schneller.
Erläuterung:
Die Rotation erfolgt um die Mantellinie des Zylinders. Nach dem Satz von Steiner gilt: Θ =
ΘS + M r 2 . Das Drehmoment der Schwerkraft lautet M gr sin α, wobei α der Neigungswinkel
der schiefen Ebene bezeichnet. Die Bewegungsgleichung lautet also:
M gr sin α = (ΘS + M r 2 )ω̇
Name
Die Translationsbeschleunigung lautet:
M gr 2 sin α
a = r = ω̇ = (Θ
2
S +M r )
Vorname
Der Massivzylinder besitzt ein Trägheitsmoment ΘS = 21 M r 2 , der dünnwandige Hohlzylinder
ΘS = M r 2 .
Legi-Nummer
D-PHYS D-MATH D-CHEM
B. Inelastischer Stoss
Ein Teilchen der Masse m und (nicht relativistischer) Geschwindigkeit v trifft frontal auf ein
zweites, im Laborsystem ruhendes, Teilchen der Masse M = 2m. Welcher Anteil der ursprünglichen kinetischen Energie ist nach dem vollkommen inelastischen Stoss noch vorhanden?
die Hälfte
⊠ ein Drittel
Wegen der Energieerhaltung bleibt die kinetische Energie unverändert.
Erläuterung:
Aus der Impulserhaltung folgt
Anzahl Punkte:
vf
vi
=
m
m+M
=
1
3
C. Kind auf Rutschbahn
Ein Kind gleitet eine reibungsfreie Rutschbahn hinunter (Abbildung 1). Wie gross muss der
Radius am Ende der Rutschbahn mindestens sein, damit das Kind den Kontakt nicht verliert?
52 H
51 H
⊠ 32 H
Erläuterung:
2
Es muss g > vR sein, und v folgt aus mg(H − R) = 21 mv 2 . Setzt man v 2 = 2g(H − R) in die
Ungleichung ein, erhält man R > 2H/3.
Himmelskörper, auch auf nicht geschlossenen Bahnen. Physikalisch gesehen ist das 2. Kepler’sche Gesetz ein Beispiel für den Drehimpulserhaltungssatz.
d) Alle Planeten bewegen sich auf elliptischen Bahnen um die Sonne, wobei die Sonne in einem
der Brennpunkte der Ellipse steht.
Dies ist das 1. Kepler’sche Gesetz. Dieses Gesetz ergibt sich aus dem Newton’schen Gravitationsgesetz, sofern die Masse des Zentralkörpers (Sonne) wesentlich grösser als die der Trabanten (Planeten) ist (M⊙ ≫ mTrabant ) und die Wechselwirkung der Trabanten untereinander
vernachlässigt werden kann.
Abbildung 1: Kind auf Rutschbahn
D. Kind auf Karussell
Ein Kind (m = 25 kg) springt mit der Geschwindigkeit v = 3 m/s auf ein stillstehendes Karussell (Ikar = 500 kg m2 , R = 2 m). Mit welcher Kreisfrequenz dreht sich das Karussell mit
dem Kind?
0.54 rad/s
0.67 rad/s
⊠ 0.25 rad/s
Erläuterung:
Die Kreisfrequenz folgt aus der der Drehimpulserhaltung: Li = mRv = (mR2 + Ikar )ωf = Lf
150
rad/s = 0.25 rad/s
gelten. Dann ist ωf = mRmRv
= 100+500
2 +I
kar
E. Keplersche Gesetze
Welche der folgenden Aussagen entsprechen Keplerschen Gesetzen?
⊠ Die Verbindungslinie zwischen der Sonne und irgendeinem Planeten überstreicht in gleichen
Zeitabständen die gleiche Fläche.
Alle Planeten bewegen sich auf kreisförmigen Bahnen um die Sonne, wobei die Sonne in
einem der Brennpunkte des Kreises steht.
Die Verbindungslinie zwischen der Sonne und irgendeinem Planeten überstreicht in gleichen
Zeitabständen die gleiche Fläche, auch wenn der Drehimpuls nicht erhalten ist (L(t) 6= const.).
⊠ Alle Planeten bewegen sich auf elliptischen Bahnen um die Sonne, wobei die Sonne in einem
der Brennpunkte der Ellipse steht.
Die Verbindungslinie zwischen der Sonne und irgendeinem Planeten überstreicht in gleichen
Zeitabständen nicht die gleiche Fläche.
⊠ Die Quadrate der Umlaufzeiten der Planeten sind proportional zu den Kuben der mittleren
Abstände der Planeten von der Sonne.
Erläuterung:
a) Die Verbindungslinie zwischen der Sonne und irgendeinem Planeten überstreicht in gleichen
Zeitabständen die gleiche Fläche.
1
Dies ist das 2. Kepler’sche Gesetz: Ḟ = dA
dt = 2m L, wobei Ḟ die sogenannte Flächengeschwindigkeit bezeichnet, dA ein infinitesimales Flächenelement und L den Drehimpuls des
Planeten. Kepler formulierte das Gesetz nur für Planeten und die Sonne, es gilt aber für alle
f) Die Quadrate der Umlaufzeiten der Planeten sind proportional zu den Kuben der mittleren
Abstände der Planeten von der Sonne.
2
4π 2 3
Dies ist das 3. Kepler’sche Gesetz: T 2 = G(M4π⊙ +m) r 3 ≈ GM
r , falls M⊙ ≫ m, wobei T die
⊙
Umlaufzeit, G die Gravitationskonstante, M⊙ die Sonnenmasse, m die Planetenmasse und r
die grosse Halbachse der Keplerellipse bezeichnet.
F. Zweiplanetensystem
Zwei Planeten gleicher Masse bewegen sich um einen Stern mit wesentlich grösserer Masse, d.h.
m1 , m2 ≪ M (Abbildung 2). Planet 1 habe die Masse m1 , und bewege sich auf einer Kreisbahn.
Planet 2 habe die Masse m2 und bewege sich auf einer elliptischen Bahn, wobei der kleinste
Abstand r1 zum Stern gleich dem Radius der Bahn von Planet 1 sei.
Welche der folgenden Aussagen sind richtig?
Die Gesamtenergie von Planet 1 ist positiv, während die von Planet 2 negativ ist.
Die Geschwindigkeit von Planet 1 im Punkt A’ ist kleiner als diejenige, welche er im Punkt
P besitzt.
⊠ Aus der Kenntnis von r1 , T1 (Umlaufdauer) und G (Gravitationskonstante) kann die Masse
M des Sterns abgeschätzt werden.
Die Gesamtenergie von Planet 1 ist grösser als die von Planet 2.
⊠ Die Geschwindigkeit von Planet 2 im Punkt A ist kleiner als diejenige, welche er im Punkt
P besitzt.
⊠ Die Gesamtenergie von Planet 2 ist grösser als die von Planet 1.
⊠ Die Gesamtenergien beider Planeten sind negativ.
Die Geschwindigkeit von Planet 1 im Punkt A’ ist grösser als diejenige, welche er im Punkt
P besitzt.
Erläuterung:
3. Dies folgt aus dem 3. Kepler’schen Gesetz.
1 ”
< v2,P .
5. Die Erhaltung des Drehimpulses führt zu v2,A = v2,P “ r1r+r
2
2
6. Im Punkt P haben beide Planeten dieselbe potentielle Energie. Da Planet 2 hier die höhere
Geschwindigkeit hat, besitzt er die höhere kinetische Energie und daher die höhere Gesamtenergie. Es ist zu beachten, dass jeder Planet eine negative Gesamtenergie hat.
7. EGesamt < 0, da es sich um gebundene Systeme handelt. Ist die Gesamtenergie gleich Null,
dann haben die Bahnen die Form einer Parabel, und wiederum können die Planeten die Bindung an den Stern überwinden. Wenn also die Gesamtenergie grösser oder gleich Null ist, dann
ist ein Planet nicht and das Gravitationsfeld des Sterns gebunden.
G. Massen an Schnur
Zwei Körper mit gleicher Masse m1 seien an den Enden einer sehr leichten Schnur (Masse ver-
r2
r1
H. Trägheitsmoment
Welche der folgenden Aussagen sind richtig?
m1
A
A’
M
Stern
Das Trägheitsmoment eines Körpers
⊠ ist dichteabhängig.
kann nur für symmetrische Körper bestimmt werden.
ist, einmal berechnet, für alle Achsen dasselbe.
⊠ Um den Steiner’schen Satz anzuwenden, muss der Schwerpunkt bekannt sein.
⊠ Trägheitsmomente sind additiv.
P
m2
Abbildung 2: Zweiplanetensystem
nachlässigbar) befestigt, die über zwei reibungsfreie, masselose Rollen laufe (Abbildung 3). Ein
dritter Körper der Masse m2 sei in der Mitte zwischen den Rollen an der Schnur befestigt. Der
Abstand der Rollen voneinander sei 2d.
Welche der folgenden Aussagen sind richtig?
~V , die von der Gewichtskraft der Masse m2 kompensiert
Die vertikale Kraftkomponente F
wird, entspricht der zweifachen Gewichtskraft von m1 .
Für die Massen m1 und m2 gilt 2m1 √h2h+d2 = m2 .
~V , die von der Gewichtskraft der Masse m2 kompensiert
⊠ Die vertikale Kraftkomponente F
wird, ist kleiner als die zweifache Gewichtskraft von m1 .
Die Länge der Schnur bestimmt die Gleichgewichtshöhe h.
Im Gleichgewicht gilt 2m1 √h2h+d2 = m2 , wobei m2 6= 2m1 .
⊠ Falls d > 0 muss m2 < 2m1 erfüllt sein, damit es eine Gleichgewichtshöhe gibt.
Erläuterungen:
!
3. Richtig, im Gleichgewicht muss gelten m2 g = 2m1 g sin θ = 2m1 g √h2h+d2 .
6. Richtig, im Gleichgewicht muss gelten: m2 − 2m1 √h2h+d2 = 0, was nur dann erfüllt ist, wenn
m2 = 2m1 √h2h+d2 < 2m1 gilt. Dies folgt auch aus der Betrachtung der potentiellen Energie
m2
√
EPot. = 2m1 g( d2 + h2 − d) − m2 gh, welche ein Minimum besitzt bei h = d s 2m1 2 .
1−
2d
θ
m1
⊠
1N
5N
25 N
100 N
500 N
Erläuterungen:
F2 = ll21 F1
J. Frictionless blocks
A 1.2-kilogram block and a 1.8-kilogram block are initially at rest on a frictionless, horizontal
surface. When a compressed spring between the blocks is released, the 1.8-kilogram block moves
to the right at 2.0 meters per second. What is the speed of the 1.2-kilogram block after the
spring is released?
⊠
1
2
3
4
m/s
m/s
m/s
m/s
θ
FZ
FZ
m
2
4m2
1
I. Zweiarmiger Hebel
An einem zweiarmigen Hebel wirkt an einem Arm mit der Länge l1 = 20 cm eine Kraft F1 = 5 N.
Welche parallel zu F1 gerichtete Kraft F2 muss an dem anderen Hebelarm mit der Länge
L2 = 100 cm angreifen, damit das gesamte Drehmoment Null ist?
Hinweis: Alle Kräfte wirken senkrecht zum Hebelarm.
FV
h
m2
g
FZ
FZ
Erläuterungen:
The total momentum of the system before releasing the spring is the same as the total momentum of the system after the release, i.e. m1 v1 = m2 v2 .
m1
FG
Abbildung 3: Massen an Schnur
K. Satellites
Two artificial satellites I and II have circular orbits of radii R and 2R about the same planet.
The orbital velocity of satellite I is v. What is the orbital velocity of satellite II?
v/2√
⊠ v/ 2
v
2v
Erläuterungen:
The velocity of the second satellite can be obtained from Keplers third law.
L. Zweites Keplersches Gesetz
Wenn die Gravitation zwischen der Sonne und den Planeten irgendwie abgeschaltet werden
könnte, und die Planeten deswegen nicht mehr auf elliptischen Bahnen die Sonne umkreisen
würden, würde dann das 2. Keplersche Gesetz immer noch zutreffen?
⊠ Ja
Nein
Erläuterungen:
Das zweite Keplersche Gesetzt beruht auf der Drehimpulserhaltung und wäre also immer noch
gültig.
M. Satellit um die Erde
Betrachte einen Satelliten, der die Erde umkreist. Welche der folgenden Aussagen ist richtig?
⊠ Je grösser sein Bahnradius, desto grösser seine Umlaufdauer.
Je grösser sein Bahnradius, desto grösser seine Geschwindigkeit.
Je grösser seine Masse, desto grösser seine Umlaufdauer.
Wenn sich der Satellit von Osten nach Westen dreht (bezüglich der Fixsterne), dann ist seine
Umlaufdauer grösser als wenn er sich von Westen nach Osten dreht.
Erläuterungen:
Fz = FG → T 2 =
Erläuterungen:
1. Falsch. Reisezeit A: x1 /v1 = 3.7y, Reisezeit B: |x2 |/v2 = 3y.
2. Richtig: totale Strecke xtot = x1 + |x2 | = 4.76Ly. t1 = xtot /(v1 + v2 ) = 3.4y.
3. Richtig: Raumschiff A und die Raumstation bewegen sich relativ zueinander mit Geschwidigkeit v1 . D.h. im Ruhesystem von Raumschiff A SA bewegt sich die Raumstation mit
Geschwidigkeit v1 .
4. Falsch. Falls v4 > v1 , dann wäre die Geschwindigkeit von Raumschiff A von B aus gesehen
grösser als c.
O. Elastische und inelastische Stösse
Welche der folgenden Aussagen sind richtig?
Der totale Impuls ist nur bei elastischen Stössen erhalten.
⊠ Die totale Energie ist sowohl bei elastischen, als auch bei inelastischen and superelastischen
Stössen erhalten.
⊠ Die totale kinetische Energie ist nur bei elastischen Stössen erhalten.
Inelastische Stösse können nur dann auftreten, wenn alle Stosspartner eine innere Struktur
besitzen.
Erläuterungen:
1. Falsch: Totale Impulserhaltung gilt auch für inelastische und superelastische Stösse.
2. Richtig: Totale Energieerhaltung gilt für alle Arten von Stössen. Zusammen mit 1. ergibt
sich 4-er Impuls-Erhaltung.
3. Richtig. Beispiel total inelastischer Stoss: Zwei einfliegende Teilchen mit Massen m1 und m2
und Geschwidigkeiten v1 und v2 kollidieren inelastisch: Teilchen 1 bleibt in Teilchen 2 stecken.
2 v2
(ImDas resultierende Teilchen hat Masse m3 = m1 + m2 und Geschwindigkeit v3 = m1 v1m+m
3
1
1
1
kin
2
2
pulserhaltung). Die kinetische Energie ist nicht erhalten: Einit = 2 m1 v1 + 2 m2 v2 6= 2 m3 v32 =
kin .
Efin
4. Falsch: Nur ein Stosspartner braucht eine innere Struktur.
4π 2 3
GM r
N. Raumstation
Ein Astronaut sitzt in einer Raumstation, welche bei x = 0 ruhend stationiert ist. Zur Zeit
t0 = 0 befindet sich bei x1 = 2.96 Ly ein Raumschiff A, welches sich mit konstanter Geschwindigkeit v1 = 0.8 c auf die Raumstation zubewegt. Ein zweites Raumschiff B befindet sich zur
selben Zeit bei x2 = −1.8 Ly, und nähert sich mit konstanter Geschwindigkeit v2 = 0.6 c der
Raumstation. Alle obigen Koordianten sind auf das Ruhesystem der Raumstation (S0 ) bezogen. Welche der folgenden Aussagen sind richtig?
P. Rolle im Trapez
Betrachte die Situation in Abbildung 4. Eine Rolle der Masse m habe die Anfangsgeschwindigkeit 0. Sie bewegt sich nun die Strecke a hinunter, welche im Winkel α < π/2 zur Waagrechten
geneigt ist. Nach passieren der Strecke b gelangt sie auf Strecke c, welche um den Winkel
β < π/2 geneigt ist. Die Höhen der beiden Plattformen sind h1 und h2 . Die Strecken a, b und
c können jeweils so beschaffen sein, dass die Rolle entweder rollt ohne zu gleiten (Material A)
oder aber gleitet ohne zu rollen (Material B). Auf die Rolle wirkt einzig die Gravitationsbeschleunigung g. Energieverluste durch Reibung sind zu vernachlässigen. Welche der folgenden
Aussagen sind richtig?
Der Astronaut auf der Raumstation sieht Raumschiff A zuerst an der Raumstation vorbeifliegen.
⊠ Auf der Raumstation vergehen 3.4 y zwischen t0 und dem Zeitpunkt t1 , zudem sich die beiden
Raumschiffe treffen.
⊠ Vom Raumschiff A (Ruhesystem SA ) aus gesehen: Die Raumstation fliegt mit der Geschwindigkeit v3 = v1 auf das Raumschiff A zu.
Vom Raumschiff B (Ruhesystem SB ) aus gesehen: Raumschiff A fliegt mit Geschwindigkeit
v4 > v1 auf die Raumstation zu.
⊠ Wenn a, b und c aus demselben Material sind, erreicht die Rolle die zweite Plattform, falls
h2 ≤ h1 .
Wenn a, b und c aus demselben Material sind, erreicht die Rolle die zweite Plattform nur
dann, wenn α = β.
⊠ Falls a und b aus √
Material B sind, beträgt die Translationsgeschwindigkeit der Rolle auf dem
Teilstück b vtrans = 2gh1 .
Erläuterungen:
1. Richtig: Falls alle Teilstücke aus dem gleichen Material sind, kann die ganze Translations-,
bzw. Rotationsenergie zum Aufstieg verwendet werden. Daher gilt: Die Rolle erreicht die zweite
Plattform, falls sie ein niedrigeres Potetial hat, d.h. gh1 ≥ gh2 → h2 ≤ h1 .
2. Falsch: Winkel spielen keine Rolle.
3. Richtig: keine Rollbewegung, d.h. keine Rotation. Daher wird die
√ ganze anfängliche Energie
2
in Translationsenergie umgewandelt: 12 mvtrans
= mgh1 → vtrans = 2gh1 .
Die Kugeln gehen zusammen in gleicher Richtung mit Geschwindigkeit 2v weiter.
Erläuterungen:
Elastischer Stoss : Die Energie bleibt erhalten. Der Impuls ist auf jeden Fall erhalten.
S. Komet um Sonne
Ein Komet beschreibt eine Ellipsenbahn um die Sonne. Man bezeichnet mit P den Punkt, wo
der Komet der Erde am nächsten zu ist, und mit M einen anderen Punkt auf der Bahn des
Kometen.
Welche der folgenden Aussagen sind richtig?
Der Betrag des Drehimpulses des Kometen ist
⊠ gleich bei P und M.
grösser bei P als bei M.
kleiner bei P als bei M.
Abbildung 4: Rollen in Trapez
Erläuterungen:
Der Drehimpuls ist erhalten, weil wir es mit einem Zentralkraftproblem zu tun haben.
Q. Störung der Kreisbahn
Man betrachtet einen sich auf einer Kreisbahn befindenden Satelliten. Man stört seine Laufbahn ein wenig (Kollision, kurze Zündung eine Rakete...). Denken Sie,
T. Absorption und Emission eines Photons
Im folgenden geht es um die Frage, ob aufgrund der Relativitätstheorie die Absorption und/oder
Emission eines Photons durch ein freies, isoliertes Elektron erlaubt ist. Welche Aussage ist
richtig?
⊠ dass er in der Nähe seiner anfänglichen Bahn bleibt; die kreisförmige Umlaufbahn ist bei
einer Störung stabil?
dass er definitiv von seiner Bahn abkommt (unstabil)?
dass er eine Kreisbahn mit einem anderen Radius einschlagen wird?
Absorption und Emission sind erlaubt, falls die Energie des Photons einen gewissen kritischen Wert nicht übersteigt.
Die Relativitätstheorie stellt nur eine Einschränkunge an den Absorptions- bzw. Emissionsprozess: Die Energie des emitierten Photons kann nicht grösser sein als die relativistische
kinetische Energie des Elektrons vor der Emission.
⊠ Freie Elektronen können weder Photonen absorbieren noch emittieren.
Erläuterungen:
Siehe Serie 2, Übung 4. Wir haben gesehen, dass es eine starke Beschleunigung braucht, damit
ein Satellit aus einer Kreisbahn kommt. Eine kreisförmige Umlaufbahn bleibt also bei schwacher Störung stabil. Andere Sichtweise : Die Kreisbahn entspricht gerade dem Minimum des
effektiven Potentials. Da es sich um ein Minimum handelt, bewirken kleine Störungen keine
Änderung (die erste Ableitung ist Null, damit verschwindet der zweite Term in der Taylorentwicklung).
Erläuterungen:
Beweis, indirekt: Es gilt Viererimpulserhaltung pµe + pµγ = pµe′ . Mit m2 c2 = (p0 )2 − ~(p)2 und
E E
pe ||~
pγ | cos θ = 0, wobei θ den Streuwinkel bezeichne. Schliesslich
mγ = 0 folgt daraus γc2 e − |~
erhält man den Widerspruch: 0 = m2e c2 + (1 − cos2 θ)p~e 2 > 0.
R. Elastische Kollision
Zwei Kugeln der gleichen Masse m mit Anfangsgeschwindigkeiten v und −v (gleicher Betrag,
entgegengesetzte Richtung) stossen elastisch frontal gegeneinander. Welche der folgenden Aussagen bezüglich der Situation nach dem Stoss sind richtig?
U. Eistänzerin
Eine Eistänzerin macht eine Pirouette mit ω = 6.28 s−1 (siehe Abb. 5 links) und richtet sich
dann auf (Abb. 5 rechts). Das jeweilige Trägheitsmoment bezgl. ihrer Drehachse ist mit T
bezeichnet. Nehmen Sie Drehimpulserhaltung an. Der Schwerpunkt bewegt sich nicht und Reibungskräfte können vernachlässigt werden.
Welche der folgenden Aussagen sind richtig?
Die Kugeln haben die Geschwindigkeit 0, denn die ganze anfängliche kinetische Energie wird
in Wärme umgewnadelt.
⊠ Die Kugeln fliegen mit einer unverminderten Geschwindigkeit vin entgegengesetzter Richtung.
Die Kugeln gehen in entgegengesetzter Richtung mit einer Geschwindigkeit vf , wobei vf < v,
denn ein Teil der anfänglichen kinetischen Energie wird in Wärme aufgelöst.
⊠ Die Winkelgeschwindigkeit nach dem aufrichten ist ω ′ = 41.9 s−1 .
Die Winkelgeschwindigkeit nach dem aufrichten ist ω ′ = 2.14 s−1 .
Es gilt Drehimpuls- und Energieerhaltung. Deshalb ist die Winkelgeschwindigkeit im aufgerichteten Zustand grösser und die kinetische Energie ändert sich nicht.
Erläuterungen:
Mit Drehimpulserhaltung gilt wegen L = ωT : ωTpirouette = ω ′ Tauf recht . Wegen Tpirouette >
Tauf recht muss also ω ′ > ω sein. D.h. a) ist richtig und b) ist falsch. Die Tänzerin muss Arbeit
leisten beim Anziehen der Gliedmassen (Zentrifugalkräfte) und deswegen ist c) falsch weil die
Energie nicht erhalten ist.
Abbildung 5: Links: Tänzerin bei Pirouette, Rechts: aufgerichtete Tänzerin
V. Wo ist der Schwerpunkt?
Zwei Wagen mit den Massen m1 = 5 kg und m2 = 10 kg sind mit einer gespannten Feder verbunden, die durch einen Faden in ihrer Spannung gehalten wird (Abbildung 6). Zum Zeitpunkt
t = 0 befindet sich der Schwerpunkt der Wagen genau im Zentrum der Wippe, dann wird der
Faden durchtrennt und die Wagen setzen sich in Bewegung (sie sind nicht fest mit der Feder
verbunden). Auf die Wagen wirkt die Schwerkraft senkrecht zur x-Achse.
Welche der folgenden Aussagen sind richtig?
Die Wippe kippt auf die Seite des schwereren Wagens, weil auf den eine grössere Schwerkraft
wirkt.
Die Wippe kippt auf die Seite des leichteren Wagens, weil der eine grössere Beschleunigung
erfährt und deshalb einen grösseren Hebel hat als der schwere Wagen.
⊠ Die Wippe kippt nicht.
Erläuterungen:
Im abgeschlossenen Gesamtsystem Wippe mit Federn, Wagen und einer Massenverteilung, die
die Schwerkraft erzeugt ist der Drehimpuls (hier bzgl. dem Wippenzentrum definiert) erhalten.
Deshalb müssen die Drehmomente, die die beiden Wagen auf die Wippe ausüben zu jedem Zeitpunkt entgegengesetzt gleich gross sein, weil sich sonst der Gesamtdrehimpuls ändern würde
und damit ist c) richtig.
Abbildung 6: Wippe
W. Notwendige Bedingung für Schwingungen
Welche Aussagen sind richtig?
Um eine harmonische Schwingung zu erhalten muss die Kraft harmonisch von der Auslenkung abhängen.
⊠ Um eine harmonische Schwingung zu erhalten muss die Kraft proportional zur Auslenkung
sein.
⊠ Um eine Schwingung zu erhalten muss die Kraft der Auslenkung entgegengesetzt sein.
⊠ Um eine harmonische Schwingung zu erhalten muss die Kraft linear und entgegengesetzt der
Auslenkung sein.
Eine harmonische Schwingung kann man der Taylor-Entwicklung eines jeden Kraftgesetzes
erhalten, aber dafür müssen die Auslenkungen klein genug sein.