12. Antennen

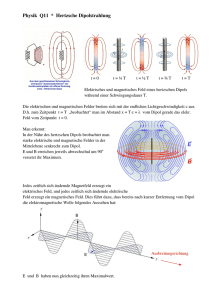
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 1
12. Antennen
Antennen übernehmen zwei Funktionen in einem Kommunikationssystem. Die Sendeantenne
wandelt die zugeführte elektromagnetische Energie aus einer Leitungswelle in eine Freiraumwelle um. Die Freiraumwelle wird in einer hinreichenden Entfernung von der Sendeantenne zu einer ebenen Welle, der die Empfangsantenne einen Teil der elektromagnetischen
Welle entnimmt und in eine Leitungswelle zurückverwandelt. Daher bezeichnet man Antennen auch als Modewandler.
Zur Beschreibung der Antennencharakteristik bedient man sich sehr häufig des Vergleiches
mit dem Modell des isotropen Kugelstrahlers. Hierzu definiert man eine punktförmige Quelle,
aus der radial und gleichmäßig die Leistung P1 austritt. Spannt man nun im Abstand r zur
Punktquelle eine Kugeloberfläche auf und deklariert das Volumen verlustfrei, so herrscht auf
der Kugeloberfläche die Strahlungsdichte:
S r  
P1
 ar
4   r 2
(12.1.1)
In der Realität besitzen Antennen die Eigenschaft, die Strahlungsdichte ungleichmäßig im
Raum zu verteilen. Die Überhöhung der Strahlungsdichte in eine bestimmte Richtung gegenüber der eines Kugelstrahlers wird mit der dimensionslosen Funktion G(), dem Gewinn einer Antenne, beschrieben. Für die in eine Richtung  des Raumes abgestrahlte Leistungsdichte einer Sendeantenne gilt somit:
S r   G1( , ) 
P1
 ar
4   r 2
(12.1.2)
Das Produkt G( , )  P gibt die adäquate Sendeleistung eines Kugelstrahlers in die entsprechende Richtung an und wird Effective Isotropic Radiated Power (EIRP) genannt.
Am Empfangsort liegt die ebene Welle mit der Strahlungsleistungsdichte S2 vor. Die empfangene Leistung hängt nun von der Wirkfläche Aw2 der Empfangsantenne ab:
P2  Aw 2  S 2 
Aw 2  G1
 P1
4   r 2
(12.1.3)
Beispiel 12.1:
Der Satellit DFS-Kopernikus sendet aus einer Höhe von 39.000 km bei ca. 12 GHz und einer
EIRP von 56 dBW nach Mitteleuropa. Wie groß ist die Empfangsleistung, wenn die Antenne
einen Durchmesser von 85 cm hat?
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 2
Kehrt man das System Sende-Empfangsantenne um und fordert, daß das die Sendeleistungen
gleich sind, so müssen auch die Empfangsleistungen gleich sein, daraus folgt:
Aw1  G2 Aw 2  G1

4   r 2 4   r 2
(12.1.4)
Aw1 Aw 2

 const
G1
G2
(12.1.5)
oder verkürzt:
Das bedeutet aber, daß das Verhältnis zwischen Wirkfläche und Gewinn in der Hauptstrahlrichtung jeder Antenne gleich groß ist. Es gilt:
Aw 0

G 4 
2
(12.1.6)
12.1 Dipolantenne
Eine Dipolantenne kann man als aufgeklappte Doppelleitung beschreiben.
Abb. 12.1.1: Von der Doppelleitung zur Dipolantenne
Der Strom im Dipol verursacht das H-Feld und die Spannung über dem Dipol das E-Feld.
Durch die endliche Ausbreitungsgeschwindigkeit der elektromagnetischen Welle kann das
Feld einer zeitlichen Veränderung der Spannung auf der Antenne nicht verzögerungsfrei folgen. Die durch die Umpolung nun entgegengesetzt wirkenden Felder drängen die zuvor entstandenen Felder von der Antenne ab. Die vollständige Loslösung der Welle erfolgt bei einem
Abstand von ca. /2.
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 3
Abb. 12.1.2: Ablösen der Welle
Ist die Dipolantenne elektrisch kurz (    ), so spricht man von einem Hertzschen Dipol. In
diesem Falle sind Strom und Spannung auf der Antenne nicht mehr ortsabhängig, sondern
konstant.
12.2 Hertzscher Dipol
Den Hertzschen Dipol kann man durch zwei Punktladungen im Abstand  beschreiben. Für
die Feldkomponenten in einem Kugelkoordinatensystem gilt dann:
H
I    1

 j  r
e  H  r ,   e
 2  j   sin   e
r
4   r
(12.2.1)
bzw.
I    1

2
 3  2  j
  sin   e  j r
E  r ,  
r 
4       0  jr
r
(12.2.2)
und
E r r ,  
I    2 2 


4       0  jr 3 r 2

  cos  e  j r

(12.2.3)
Der Hertzsche Dipol strahlt somit einen E-Mode eine TM-Welle ab.
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 4
Man erkennt, daß alle Feldkomponenten eine starke Abhängigkeit vom Radius r aufweisen,
was besonders für den E r r ,  - Feldanteil gilt. Betrachtet man die mittlere Leistung eines
Hertzschen Dipoles, so ist die Feldstruktur bei großen Radien r von Interesse. Diese Bedingung ist aber erfüllt, wenn:

1

2
r
r

r 
0
2 
(12.2.4)
gilt. Man spricht dann vom Fernfeld. Das sogenannte Nahfeld ist der Bereich
r
0
2 
(12.2.5)
Im Fernfeld haben somit nur noch Terme eine Bedeutung, die eine Abhängigkeit von 1/r aufweisen, d.h.:
H  r ,   j
I  
 sin   e  j r
2  0  r
E  r ,   jZ 0
I  
 sin   e  j r
2  0  r
E r r ,   0
(12.2.6)
(12.2.7)
(12.2.8)
Der Hertzsche Dipol strahlt im Fernfeld somit eine ebene Welle aus - ein TEM-Mode -. Daraus resultiert für den Leistungsdichte allein eine radiale Komponente:

 I  
S r r ,   Z 0 
 sin  

 2  0  r
2
(12.2.9)
Bestimmt man nun die entsprechende Leistung, die der Dipol abstrahlt, durch Integration über
eine unendlich ferne Hüllfläche, so gilt:

PD  2     S r r ,   r 2  sin   d 
0
2
2
   I
2 

 Z 0    
3
 0  2
(12.2.10)
Nimmt man nun an, daß die abgestrahlte Leistung gleich der Leistung des Dipolstromes in einem ohmschen Widerstand ist, so berechnet sich der Strahlungswiderstand RS des Hertzschen
Dipoles zu:
  
2 
RS 
 Z 0   
3
 0 
2
(12.2.11)
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 5
Die Ausbreitung der Felder kann mit den folgenden zwei Strahlungscharakteristiken beschrieben werden.
Abb. 12.2.1: Vertikale Strahlungscharakteristik
Abb. 12.2.2: Horizontale Strahlungscharakteristik
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 6
12.3 Polarisation
Die Polarisation einer elektromagnetischen Welle wird über die Schwingungsrichtung des
elektrischen Feldvektors definiert.
Von einer linearen Polarisation spricht man, wenn der Endpunkt des Vektors auf einer Geraden schwingt. Sie ist horizontal bzw. vertikal in ihrer Orientierung bezogen auf die Erdoberfläche.
Zwei linear polarisierte Wellen, deren elektrische Vektoren gleicher Amplitude räumlich und
zeitlich um 90° gegeneinander verdreht sind, d.h., die elektrischen Vektoren stehen senkrecht
aufeinander und sind um 90° in der Phase gegeneinander verschoben, setzen sich zu einer zirkular polarisierten Welle zusammen. Der Endpunkt des elektrischen Vektors bewegt sich auf
einem Kreis. Je nach Drehrichtung unterscheidet man noch zwischen einer rechts- bzw. linksdrehenden zirkularen Polarisation. Rechtsdrehend dann, wenn Drehsinn und Ausbreitungsrichtung der Welle ein Rechtssystem bilden bzw. umgekehrt. Sind die Amplituden der beiden
Vektoren ungleich groß und ist die Phasenverschiebung zwischen den Vektoren nicht gleich
90°, so spricht man von einer elliptischen Polarisation mit beliebiger Lage der Hauptachse.
Jede elliptische Polarisation läßt sich aus zwei entgegengesetzt drehenden zirkular polarisierten Wellen unterschiedlicher Amplitude zusammensetzen.
Beispiele für Polarisationen:

Lang- und Mittelwelle: vertikal

Kurzwelle, UKW und Fernsehen: horizontal und vertikal

kommerzieller UKW-Funk: vertikal

Satellitenfunk: zirkular
12.4 Babinetsche Prinzip
Das Babinetsche Prinzip findet Anwendung bei der Berechnung von Schlitzantennen. Sind
komplementäre Probleme bereits gelöst, so lassen sich die Lösungen häufig unmittelbar hinschreiben. Was steckt dahinter?
Der französische Physiker, Jacques Babinet (1794 – 1872), entwickelte das Theorem in der
Optik. Es besagt, dass das Beugungsbild zweier geometrisch komplementärer Blenden abgesehen von der geometrischen optischen Achse (nullte Beugungsordnung) auf dem Schirm
identisch ist. Beispielsweise unterscheidet sich das Beugungsbild eines Einzelspalts kaum von
dem eines Drahtes, ein Kreis nicht von einem Loch in Größe des Kreises (s. Wikipedia).
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 7
Überlagert man beide Bilder, so ist das Ergebnis gleich dem ohne jegliche Blende. Da Licht
ebenfalls elektromagnetische Wellen sind, kann man das Prinzip auch auf Antennen anwenden.
Der Sender T1 auf der linken Seite einer Blende erzeugt auf deren rechter Seite ein Strahlungsfeld S1. S1 sei dabei das Verhältnis dieses Feldes zu dem, das ohne Blende vorhanden
wäre. Der konjugierte Sender T2 links von der komplementären Blende - Schirm - erzeugt
rechts das Strahlungsfeld S2 wiederum als Verhältnis zu dem ohne Schirm. Nach Babinet gilt
nun:
S1  S 2  1
(12.4.1)
Als komplementäre Blenden oder Schirme sind Gebilde mit unendlicher Ausdehnung in der
Ebene zu verstehen. Die konjugierten Sender entstehen durch das Vertauschen von elektrischen größen mit magnetischen. Also für den Fall einer einfallenden ebenen Welle entspricht
dies dem Austausch des E-Vektors gegen den H-Vektor bzw. die Drehung der Polarisationsebene um 90 °.
Für die Herleitung des Diagramms und Widerstandes einer Schltzantenne in der Ebene bietet
es sich somit an, einen komplementären λ/2-Dipol zu berechnen. Für den Strom im Dipol findet man:
I  V / Za 
E0 
  Za
(12.4.2)
Mit Za =73 Ω und V bzw. I als Klemmenspannung und -strom des komplementären Dipols.
Das Feld E0 liegt dabei parallel zum Dipol und das konjugierte Feld somit quer zum Schlitz
polarisiert. Es gilt dann für den Dipol:
E  j

60    E 0 cos( 2 cos )  j0 r

e
73    r
sin 
1
 E
Z0
(12.4.3)
E   Z 0  H 
(12.4.4)
H 
Für die äquivalente Schlitzantenne erhält man somit:
H   j

60    H 0 cos( 2 cos )  j0 r

e
73    r
sin 
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik
QUIRDER
HOCHFREQUENZTECHNIK
ANTENNEN
12 - 8
12.5 Fractale Antennen
Mit der Vorgabe Multifrequenzanwendungen zu ermöglichen und dabei gleichzeitig die Baugröße der Antenne immer kleiner und kompakter zu gestalten, hat man die nach Mandelbrot
definierten Fraktale, also geometrische Objekte mit selbstähnlichen Formen, auf das Layout
von Antennen angewandt. Das Entscheidende ist dabei, dass fraktale Kurven die mathematische Eigenschaft haben, den vorgegebenen Raum besser auszunutzen als jede klassische euklidische Oberfläche. Daraus resultiert die kleinstmögliche Größe einer Antenne für die gestellte Anforderung.
Eine besonderes Exemplar ist die sogenannte Sierpinski Monopolantenne. In der Abbildung
12.5.1 skizzierten Antenne wurde der Sierpinski fractal-Algorithmus vier Mal wiederholt.
Abb. 12.5.1 Sierpinski Monopolantenne 1)
Über die Bandbreite weist die Struktur ein nahezu logarithmisches Verhalten auf, das sich wie
folgt beschreiben lässt:
f m  0,26  c / h   n
(12.5.1)
mit c der Lichtgeschwindigkeit, h der Höhe bis zur Oberkante und δ der logarithmischen Basis, die in diesem Falle gleich 2 ist, da nach der 4. Näherung 24 schwarze Dreiecke vorhanden
sind.
1
) Fusco, Vincent F.: Foundations of Antenna Theory and Techniques, Pearson Education Ltd, England, 2005,
S. 198
Fachhochschule Frankfurt am Main - University of Applied Sciences
Elektrotechnik / Informationstechnik