Einführung in die Astronomie unf Astrophysik I - Teil 12
Werbung

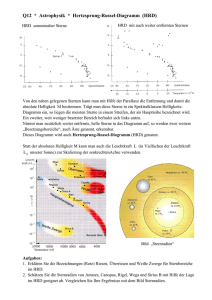
Astro-Semester-Abschlussveranstaltung Wer? Alle an der UHH, die irgendwie mit Astro zu tun haben Wo? Hamburger Sternwarte Gojenbergsweg 112 21029 Hamburg Wann? Freitag, 15. Juli 2016, 14:00 Was? Führung durch die Stermwarte, Kaltgetränke, Erhitzung von Essbarem durch die Bestrahlung mit Schwarzkörperstrahlung Astronomische Nachricht der Woche Astronomische Nachricht der Woche Astronomische Nachricht der Woche Am 5. Juli kam Juno am Jupiter an Erfolgreiche “orbit insertion” Stark elliptische Umlaufbahn mit zunächst P = 53.5 d Später: P = 14 d Einführung in die Astronomie und Astrophysik I Teil 12 Jochen Liske Hamburger Sternwarte [email protected] Themen Einstieg: Was ist Astrophysik? Koordinatensysteme Astronomische Zeitrechnung Sonnensystem Die Keplerschen Gesetze Himmelsmechanik Gezeiten und Finsternisse Strahlung Helligkeiten Teleskope Extrasolare Planeten Charakterisierung von Sternen Sterne: Äußere Schichten Sterne: Innerer Aufbau Sterne: Hertzsprung-Russell-Diagramm HRD setzt zwei fundamentale Größen von Sternen miteinander in Beziehung: Gesamtstrahlungsleistung und Strahlungsfluss durch Oberfläche In diesem Parameterraum besetzen Sterne nur bestimmte Regionen Diese entsprechen verschiedenen Entwicklungsstadien von Sternen Zentrales Element für unser Veständnis von Sternen und deren Entwicklung Sterne: HRD Verschiedene Regionen im HRD entsprechen verschiedenen Entwicklungsstadien: Hauptreihe: “Normalzustand” von Sternen, H-Brennen, hier verbringen Sterne die meiste Zeit ihres Lebens Riesen: spätere Entwicklungsphasen Weiße Zwerge: Endzustand von Sternen bestimmter Masse (die anderen möglichen Endzustände sind nicht im HRD vertreten: Neutronensterne, Schwarze Löcher) Sterne: HRD Verschiedene Regionen im HRD entsprechen verschiedenen Entwicklungsstadien: Hauptreihe: “Normalzustand” von Sternen, H-Brennen, hier verbringen Sterne die meiste Zeit ihres Lebens Riesen: spätere Entwicklungsphasen Weiße Zwerge: Endzustand von Sternen bestimmter Masse (die anderen möglichen Endzustände sind nicht im HRD vertreten: Neutronensterne, Schwarze Löcher) Die „Bevölkerungsdichte“ der verschiedenen Regionen lässt auf die Dauer der Entwicklungsphasen schliessen 30,000 Sterne mit Parallaxen von HIPPARCOS Sterne: HRD Verschiedene Regionen im HRD entsprechen verschiedenen Entwicklungsstadien: Hauptreihe: “Normalzustand” von Sternen, H-Brennen, hier verbringen Sterne die meiste Zeit ihres Lebens Riesen: spätere Entwicklungsphasen Weiße Zwerge: Endzustand von Sternen bestimmter Masse (die anderen möglichen Endzustände sind nicht im HRD vertreten: Neutronensterne, Schwarze Löcher) Die „Bevölkerungsdichte“ der verschiedenen Regionen lässt auf die Dauer der Entwicklungsphasen schliessen Allgemein: HRD extrem wichtig, um unser Verständnis der Entwicklung von Sternen zu überprüfen Sterne: HRD Verschiedene Regionen im HRD entsprechen verschiedenen Entwicklungsstadien: Hauptreihe: “Normalzustand” von Sternen, H-Brennen, hier verbringen Sterne die meiste Zeit ihres Lebens Riesen: spätere Entwicklungsphasen Weiße Zwerge: Endzustand von Sternen bestimmter Masse (die anderen möglichen Endzustände sind nicht im HRD vertreten: Neutronensterne, Schwarze Löcher) Die „Bevölkerungsdichte“ der verschiedenen Regionen lässt auf die Dauer der Entwicklungsphasen schliessen Allgemein: HRD extrem wichtig, um unser Verständnis der Entwicklung von Sternen zu überprüfen Umgekehrt: Verständnis vorausgesetzt, können Merkmale des HRD z.B. zur Altersbestimmung von Sternpopulationen benutzt werden Sterne: Hauptreihe Wasserstoffbrennen im Kern “Normalzustand” Längste Phase eines Sternenlebens Ist mehr oder weniger 1-dimensional Hinweis auf einfachen Zusammenhang zwischen M, R, L, Teff Nur 1 Parameter für Beschreibung nötig? Sterne: Hauptreihe Empirisch findet man für Hauptreihensterne Beziehungen zwischen M und L, R: L M3.5 R M0.8 Exponenten leicht massenabhängig Beziehungen können mit vereinfachenden Annahmen auch theoretisch hergeleitet werden Aus L = 4 R2 σTeff4 log Teff = 0.5 log M + const Hauptreihe ist eine 1-Parameter Sequenz Masse ist das zentrale Charakteristikum für Hauptreihensterne Veränderliche Sterne Die meisten Sterne haben eine gleichbleibende Helligkeit Beispiel Sonne: Variabilität < 1% Physische (oder intrinsische) Veränderliche Beschreibung mit Lichtkurve: s(t) Großes Spektrum von beobachteten Helligkeitsschwankungen: von gerade noch messbar bis Schwankungen um viele Größenordnungen Verschiedene Periodizitäten • Regellose Lichtkurven • Einmalige Veränderliche • Periodische Veränderliche • Zeitskalen: Sekunden – viele Jahre Extrinsische Veränderliche Bedeckung Rotation Veränderliche Sterne Viele Veränderliche zeigen ähnliches Verhalten und finden sich im HRD in derselben Region Einordnung in Typen möglich Viele verschiedene Typen Benennung nach Prototypen, z.B. Mira = o Ceti (Beobachtung bereits 1594) • langperiodische Veränderliche später Typen + Roter Riesen δ Cephei Cepheiden • Überriesen mit fester Periode RR Lyrae (auch: Haufenveränderliche) • kurz-periodische A-Sterne T-Tauri Sterne • Junge Sterne, Vor-Hauptreihensterne Veränderliche Sterne Veränderliche Sterne Physikalische Unterscheidung: Pulsationsveränderliche Helligkeitsschwankung durch Leuchtkraftänderung Meist radiale Pulsation des Sterns Eruptive Veränderliche Massenverluste (Riesen) Akkretionsphänomene (junge Sterne) Kataklysmische Veränderliche Thermonukleare Reaktionen Veränderliche Sterne: Cepheiden Streng periodische Pulsationsveränderliche Riesensterne Mehrere Subtypen Amplituden: < 2 mag Perioden: 1 – 130 d Empirische Leuchtkraft-PeriodeBeziehung: L ~ Pn M = -2.8 log (P/1d) – 1.4 Standardkerzen für Entfernungsbestimmung! Sterne: äußere Schichten Photosphäre Chromosphäre Korona Aktivität Modellierung Sterne: äußere Schichten Sterne sind Gaskugeln im Gleichgewicht zwischen Eigengravitation und innerem Druck Energiequelle: Kernfusion, nicht direkt sichtbar Nur die äußeren Schichten sind sichtbar Hier: Diskussion am Beispiel der Sonne Einteilung des sichtbaren Bereichs / Außenzonen Photosphäre: sichtbare (optisch) Oberfläche Chromosphäre: dünne, heiße Schicht Korona: sehr heiße ausgedehnte Region Sterne: äußere Schichten Photosphäre Die meiste optische EM-Strahlung wird an der Übergangsregion optisch dicht optisch dünn emittiert Photosphäre (“Lichtkugel”) Ausdehnung ca. 300 km (0.04% R⨀) scharf begrenzter Rand (nur bei der Sonne ohne weiteres beobachtbar) Bestimmt Spektrum der Strahlung: Kontinuum + Absorptionslinien Dichte: 10−4 10−5 kg/m3 T: 6400 4400 K Photosphäre Helligkeit nimmt zum Rand hin ab Randverdunkelung Effekt stärker bei kleineren Wellenlängen Photosphäre Granulation: Hell-Dunkel-Struktur bedingt durch tiefer liegende Konvektionszone ΔT = 200 – 300 K ⌀: bis zu 1000 km Lebensdauer: einige Minuten Chromosphäre Schicht überhalb der Photosphäre: Δh ~ 2000 km Dichte fällt schnell ab: 10−8 kg/m3 ≈ 10−3 ρPhoto Temperatur steigt an: bis 25.000 K, Grund nicht klar Aber: SChrom ~ 10−4 SPhoto Emissionslinien: z.B. Hα Chromosphäre erscheint rot Sterne: äußere Schichten Chromosphäre Protuberanzen Plasmabögen Entstehen und kollabieren schnell (1d), Lebensdauer bis zu Monaten ~105 km Spikulen Plasmaeruptionen Lebensdauer: Minuten ~103 km Chromosphäre Korona Stark verdünnte, sehr heiße Hülle ρ ~ 10−15 kg/m3 T > 106 K SKorona ~ 10−6 SPhoto Nur bei totaler Sonnenfinsternis sichtbar Kontinuierliches Spektrum im Optischen Photosphärenlicht wird an sehr “heißen” Elektronen gestreut Absorptionslinien verschwinden Korona Korona Hoch ionisierte Emissionslinien sichtbar, z.B. Fe13+, Ca14+ Korona ist sehr heiß Eigenstrahlung im Röntgenbereich Korona Aufheizung der Korona? Wärmetransport von “kalter” Photosphäre nicht möglich Magnetisch-akustische oder Alfvén Wellen? Umwandlung der Magnetfeldenergie in Wärme? Indikator Plasmabögen: Gas strömt entlang Magnetfeldlinien Korona Koronale Massenauswürfe 106 km und mehr 1012 kg Bis zu 3000 km/s Frequenz: 1/Woche – mehrere/Tag Sterne: äußere Schichten Sonnenwind Entweichen von Koronamaterie kontinuierlicher Teilchenstrom aus p, e-, α Schnelle Komponente: 750 km/s, langsame: ~400 km/s Verlustrate: 1035 – 1036 Teilchen/s 10−15 – 10−14 M⨀/yr ~106 t/s! Schwankung durch Sonnenaktivität Magnetfeld der Erde lenkt Strom um Polarlichter Stoßfront mit interstellarem Gas Heliopause (50 − 100 AU)? Sonnenaktivität Viele dynamische Phänomene: Granulation und Supergranulation Protuberanzen und Spikulen Koronale Massenauswürfe Sonnenwind Sonnenflecken Gemeinsame Ursache: Wechselwirkung zwischen differentieller Rotation und Magnetfeldern, Freisetzung von in Magnetfeldern gespeicherter Energie Credit: SDO Sonnenflecken Orte, an denen Magnetfellinien die Sonnenoberfläche durchstoßen Kern (Umbra) + Rand (Penumbra) ⌀: bis zu 50.000 km Lebensdauer: Tage bis zu 4 Monate Treten in Paaren, oft in Gruppen auf Starke Magnetfelder: 4000 G behindern Konvektion Temperaturerniedrigung um ΔT ≈ 2000 K dunkler Sonnenflecken Häufigkeit der Sonnenflecken variiert 11 Jahres Zyklus = 1/2 Zyklus des Dipol-Magnetfelds Maunder-Minimum kleine Eiszeit Sonnenflecken Physik der Sternatmosphären Atmosphäre = äußere, dünne, durchlässige, d.h. sichtbare Schichten Prägt das Spektrum der Sternstrahlung Spektralanalyse Charakterisierung durch Teff, log g, chemische Zusammensetzung Muss große Energiemengen von innen nach außen transportieren Physik der Sternatmosphären Beschreibung durch: Hydrostatisches Gleichgewicht • „Druck = Gravitation“ Strahlungstransport • Energietransport hauptsächlich durch Strahlung (Konvektion spielt nur bedingt eine Rolle) Energieerhaltung • F(r) = σ Teff4 = const Randbedingungen Resultat: Druck P(r) Temperatur T(r) Dichte (r) spektrale Intensität I Physik der Sternatmosphären Annahmen: Dünne Atmosphäre: datmo << R • Konstante Gravitationsbeschleunigung • Planparallele Schichten im hydrostatischen Gleichgewicht Strahlungstransport im lokalen thermodynamischen Gleichgewicht • Als Ganzes ist die Atmosphäre nicht im globalen thermodynamischen Gleichgewicht (GTE): Energietransport nach außen Temperatur nimmt i.d.R. nach außen ab • Aber in dünner Schichtung kann TE angenommen werden Strahlungstransport Energieaustausch zwischen zwei Schichten der Atmosphäre wird durch Strahlung vermittelt Das Gas in jedem Volumenelement absorbiert (und streut) die eintreffende Strahlung I und re-emittiert sie wieder Strahlung muss sich von den dichten inneren Schichten zu den dünneren äußeren Schichten „vorarbeiten“, bevor sie schließlich entkommen kann „random walk“ der Photonen vom Sterninneren an die „Oberfläche“ Temperaturgradient ist unerlässlich Re-Emission i.d.R. isotrop benachbarte Schichten bestrahlen sich gegenseitig Eine Nettoenergiefluss kann nur dann zustande kommen, wenn eine Schicht heißer ist als die andere Strahlungstransport Strahlungstransport Strahlungstransport Strahlungstransport Strahlungstransport Photosphäre Helligkeit nimmt zum Rand hin ab Randverdunkelung Effekt stärker bei kleineren Wellenlängen Photosphäre Verlauf der Strahlungsintensität: T steigt nach innen an B(,T) nimmt zu Aber optische Tiefe nimmt auch zu exp(−) nimmt schnell ab Größter Beitrag bei ≈ 1 Zum Rand hin wird ≈ 1 schon in größeren geometrischen Höhen erreicht und somit bei niedrigeren Temperaturen und Strahlungsintensitäten Randverdunkelung (limb darkening) Bestimmung des vertikalen Temperaturverlaufs der Photosphäre Photosphäre Verlauf der Strahlungsintensität: T steigt nach innen an B(,T) nimmt zu Aber optische Tiefe nimmt auch zu exp(−) nimmt schnell ab Größter Beitrag bei ≈ 1 Zum Rand hin wird ≈ 1 schon in größeren geometrischen Höhen erreicht und somit bei niedrigeren Temperaturen und Strahlungsintensitäten Randverdunkelung (limb darkening) Bestimmung des vertikalen Temperaturverlaufs der Photosphäre Chromosphäre / Korona Physik der Sternatmosphären Beschreibung durch: Hydrostatisches Gleichgewicht • „Druck = Gravitation“ Strahlungstransport • Energietransport hauptsächlich durch Strahlung (Konvektion spielt nur bedingt eine Rolle) Energieerhaltung • F(r) = σ Teff4 = const Randbedingungen Resultat: Druck P(r) Temperatur T(r) Dichte (r) spektrale Intensität I Physik der Sternatmosphären Annahmen: Dünne Atmosphäre: datmo << R • Konstante Gravitationsbeschleunigung • Planparallele Schichten im hydrostatischen Gleichgewicht Strahlungstransport im lokalen thermodynamischen Gleichgewicht • Als Ganzes ist die Atmosphäre nicht im globalen thermodynamischen Gleichgewicht (GTE): Energietransport nach außen Temperatur nimmt i.d.R. nach außen ab • Aber in dünner Schichtung kann TE angenommen werden Modellierung von Sternatmosphären Input: Effektivtemperatur Teff Leuchtkraft L Oberflächenbeschleunigung g Chemische Zusammensetzung Aber: abhängig von P, ρ, T Ziel / Output: Bestimmung von P(r), ρ(r), T(r) Strahlungsfeld I Spektrum (Aussehen des Stern) Modellierung von Sternatmosphären Gleichungen: Hydrostatisches Gleichgewicht: Zustandsgleichung: ideales Gas Strahlungstransport Energieerhaltung Materialfunktion (schwer zugänglich) = (T, P, , chem. Zusammensetzung) numerische Integration liefert P(r), ρ(r), T(r) d.h. Modellatmosphären Hydrostatisches Gleichgewicht Modellatmosphären Photosphäre Chromosphäre Analyse von Sternspektren Ziel: aus dem beobachteten Spektrum eines Sterns auf die Struktur und chemische Zusammensetzung seiner Atmosphäre zu schließen Iterativer Prozess: 1. Start mit T, g, chemischer Zusammensetzung 2. Berechnung der Modellatmosphäre • Aus ρ(r), P(r), T(r) und chemischer Zusammensetzung kann die spektrale Verteilung F eindeutig bestimmt werden 3. Berechnung des synthetischen Spektrums 4. Detaillierter Vergleich mit beobachteten Spektrum • Kontinuum • Relative und absolute Stärke möglichst vieler Absorptionslinien • Linienprofile Falls signifikante Unterschiede: 5. Modifikation der Input-Parameter 6. Zurück zu 1. Spektralanalyse Wie kommen die Absorptionslinien in das Spektrum? Erinnerung: Atome und Moleküle können Photonen bestimmter Wellenlängen absorbieren, z.B. elektronische Übergänge (g-g, g-f, …) Berechnungen und Messungen aus der Atomphysik liefern: Absorptionsquerschnitt für jedes Atom/Ion X: a,X Gesamt-Linien-Absorptionskoeffizient: Spektralanalyse Entstehung von Absorptionslinien ähnlich wie Randverdunkelung: Bei λ = λc,Linie ist größer als außerhalb einer Linie = 1 in größerer geometrischer Höhe, wo Atmosphäre kühler und weniger hell ist weniger Strahlung im Linienzentrum als außerhalb „Absorptions“linie Spektrallinien Linienverbreiterung durch Natürliche Linienbreite (wg. endlicher Lebensdauer, Lorentz-Profil) Doppler-Verbreiterung (Gauss-Profil) Druckverbreiterung (Lorentz-Profil) Turbulenz (Gauss-Profil) Linienprofil-Analyse gibt Information über Druck, Schwerebeschleunigung, Temperatur und Gasströmungen Spektrallinien Doppler-Verbreiterung Durch thermische Bewegung des Gases Maxwell-Boltzmann-Verteilung der Geschwindigkeiten bestimmt Linienverbreiterung: Für T ~ 5000 K relative Linienbreite: ~10−5 (abhängig vom betrachteten Atom/Ion) Spektrallinien Druck-/Stoßverbreiterung Durch Stöße mit benachbarten Atomen (Strahlungsdämpfung) Lorentzprofil = Dämpfungskonstante Doppler + Druckverbreiterung Voigt-Profil: Spektrallinien Beispiel: CaII H+K Linien Stark temperaturabhängig Wenig druckabhängig Spektralanalyse Wie kommen die Absorptionslinien in das Spektrum? Erinnerung: Atome und Moleküle können Photonen bestimmter Wellenlängen absorbieren, z.B. elektronische Übergänge (g-g, g-f, …) Berechnungen und Messungen aus der Atomphysik liefern: Absorptionsquerschnitt für jedes Atom/Ion X: a,X Gesamt-Linien-Absorptionskoeffizient: Spektralanalyse Wie kommen die Absorptionslinien in das Spektrum? Erinnerung: Atome und Moleküle können Photonen bestimmter Wellenlängen absorbieren, z.B. elektronische Übergänge (g-g, g-f, …) Berechnungen und Messungen aus der Atomphysik liefern: Absorptionsquerschnitt für jedes Atom/Ion X: a,X Gesamt-Linien-Absorptionskoeffizient: Spektralanalyse Stärke einer Absorptionslinie hängt von Dichte des entsprechenden Ions im entsprechenden Anregunszustand ab Also von: Häufigkeit des Elements, Ionisationsgrad, Anregungsgrad Müssen mit Hilfe mehrerer Linien selbst-konsistent bestimmt werden Für LTE: Anregungszustand bei Temperatur T durch BoltzmannGleichung beschrieben Ionisationsgrad durch Saha-Gleichung Spektralanalyse Boltzmann-Gleichung: bei Temperatur T ist die Teilchendichte im angeregten Zustand s im Verhältnis zur Teilchendichte im Grundzustand gegeben durch: ns: Teilchendichte im Zustand s gs: Statistisches Gewicht des Zustands s s: Energie des Zustands s Spektralanalyse Saha-Gleichung: bei Temperatur T ist die Dichte der Teilchen, die (r+1)-fach ionisiert sind, im Verhältnis zur Dichte der Teilchen, die r-fach ionisiert sind, gegeben durch: nr: Dichte der Teilchen, die r-fach ionisiert sind ne: Elektronendichte ur = Σi gi exp(−i / kBT): Zustandssumme über alle Anregungszustände im r-fachen Ionisationszustand r: Ionisationsenergie, die für den Übergang Grundzustand r-fach ionisiert Grundzustand (r+1)-fach ionisiert benötigt wird Spektralanalyse Zusammenspiel von Boltzmann- und Saha-Gleichung Erklärung der Spektraltypen als Funktion von Teff Variation der Linienstärken hat nichts mit unterschiedlichen Elementhäufigkeiten als Funktion des Spektraltyps zu tun! Elementhäufigkeiten Bestimmung der Elementhäufigkeit trotzdem möglich Angabe normalerweise logarithmisch, relativ zu H und dem gleichen Verhältnis in der Sonne: Elementhäufigkeiten H am häufigsten: ~70% der Masse, ~90% der Teilchen He: ~27% der Masse, ~10% Teilchen Rest: „Metalle“ Im Allgemeinen bergen die relativen Elementhäufigkeiten Information über die Entstehungsgeschichte(n) der Elemente (Nukleosynthese kurz nach Urknall, in Sternen, Supernovae) Im Besonderen bergen die relativen Elementhäufigkeiten eines Sterns Information über die Entstehungsgeschichte des Sterns, z.B. Korrelation zwischen Metallizität und Alter