Text 1
Werbung

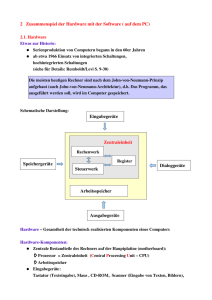
Тексты по немецкому языку для индивидуального чтения для студентов специальности 1-400201 (ВС), 1-400101 (ИТ) Text 1 Mathematik - Zahlenbereiche Vorübungen 1. Welche der folgenden Begriffe sind Internationalismen, die Sie bereits kennen? Übersetzen Sie sie. -e Addition • -e Dezimalzahl • irrational • -e mathematische Operation • -e Menge • -e Multiplikation • negativ • periodisch • positiv • -r Radikand • rational • reell • subtrahieren • -s Symbol • unendlich Zahlenbereiche Man kann ohne Übertreibung behaupten, dass der Begriff der Menge das Fundament der modernen Mathematik bildet. Alle Theorien sind mengentheoretisch aufgebaut. Eine Zahlenmenge ist eine genau definierte Menge von Zahlen. In der Regel werden unter diesem Begriff nicht nur die Elemente einer Menge verstanden, sondern auch die verschiedenen mathematischen Operationen, die man in diesen Mengen uneingeschränkt durchführen kann. Natürliche Zahlen (Symbol: N) sind aus dem Grundbedürfnis der Menschen erwachsen, Dinge zu zählen, d.h. die Anzahl von Elementen zu bestimmen. Unter ihnen versteht man die Menge aller positiven ganzen Zahlen. Zuweilen wird ihnen auch noch die neutrale Zahl 0 zugerechnet. Die Zahl Null ist weder negativ noch positiv. Manche Lehrbücher notieren diesen Zahlbereich dann als N0. Addition und Multiplikation sind uneingeschränkt möglich. Zum Beispiel: 3 + 4 = 7, aber 3 - 4 gibt kein Ergebnis in N. Die Menge umfasst die Zahlen 1, 2, 3, 4, 5, 6 usw. Zusammen mit der Null und negativen ganzen Zahlen, z. B. -1, -2, -3, …, bilden sie die Menge der ganzen Zahlen. (Symbol: Z „ganze Zahlen"). Die ganzen Zahlen erweitern die natürlichen Zahlen um negative ganze Zahlen. Mit ihnen ist es möglich, uneingeschränkt zu subtrahieren. Beispiel: 3-4 = -1. Die Menge umfasst die Zahlen ..., -3, -2, -1, 0, 1, 2, 3,... Im Rahmen dieser Menge unterscheiden wir gerade Zahlen, z. B. 2, 4, 6, -2, -4,..., die durch zwei teilbar sind, und ungerade Zahlen, z.B. -5, -3, 3, 5,..., die nicht durch zwei teilbar sind. Die Menge der ganzen Zahlen zusammen mit der Menge aller Brüche bildet die rationalen Zahlen (Symbol: Q). Diese lassen sich als Verhältnis zweier ganzer Zahlen darstellen, z.B. 1/3, 2/5. Jeder Dezimalbruch lässt sich auch als Dezimalzahl schreiben, z. B. 1/4 oder 0,25. Die Menge der rationalen Zahlen und die der irrationalen Zahlen bilden zusammen die Menge der reellen Zahlen (Symbol: R). Die reellen Zahlen bilden eine Synthese aus den rationalen Zahlen und den irrationalen Zahlen – unendliche, nicht periodische und demzufolge nicht als Bruch darstellbare Zahlen. Das Ziehen der Wurzel bei positivem Radikand kann nun eindeutig durchgeführt werden. Beispiele: √2, 3√7, π. Leseverstehen 2. Lesen Sie den Text ein erstes Mal und achten Sie auf die fett gedruckten Ausdrücke. Ordnen Sie dann die folgenden Begriffe den Symbolen in der Tabelle zu. natürliche Zahlen • ganze Zahlen • rationale Zahlen • reelle Zahlen 1 ) Q – _____________________ 3) Z– _________________________ 2 ) N – _____________________ 4 ) R – ________________________ 3. Ordnen Sie die Symbole aus Aufgabe 2 in das Schema ein. _ [0];1; 2; 3; … _ ...-3; -2; -1 _ -7,25; -½; 2¾ _ π; e; √2; -1; 0; 7,25 4. Lesen Sie den Text beim zweiten Mal genauer und ordnen Sie die Satzteile einander zu. Beispiel:1c 1) Zu der Menge der natürlichen Zahlen gehören ... 2) Die positiven ganzen Zahlen, die Null und die negativen ganzen Zahlen ... 3) Im Rahmen der ganzen Zahlen unterscheiden wir ... 4) Die Zahl Null ist ... 5) Die rationalen Zahlen kann man als Verhältnis ... 6) Die reellen Zahlen lassen sich nicht... a) b) c) d) e) weder negativ noch positiv gerade und ungerade Zahlen. alle positiven ganzen Zahlen. zweier ganzer Zahlen darstellen. bilden zusammen die Menge der ganzen Zahlen. f) als Bruch zweier ganzer Zahlen schreiben. 5. Welche der folgenden Aussagen sind richtig, welche falsch? Kreuzen Sie an und korrigieren Sie die falschen Aussagen. 1) Zu der Menge der natürlichen Zahlen gehören negative ganze Zahlen. 2) Die Null gehört nicht zu der Menge der natürlichen Zahlen. 3) Gerade Zahlen lassen sich durch zwei teilen. 4) Die Zahl Null ist positiv. 5) Rationale Zahlen kann man nicht als Verhältnis zweier ganzer Zahlen darstellen. 6) Jeder Dezimalbruch ist auch als Dezimalzahl schreibbar. 7) Reelle Zahlen kann man als Bruch zweier ganzer Zahlen schreiben. 8) Die Menge der reellen Zahlen bilden rationale und irrationale Zahlen. 6a. Brüche bestehen aus dem Zähler über dem Bruchstrich und dem Nenner unter dem Bruchstrich. Unterstreichen Sie bei den folgenden Begriffen die Endungen der Nenner und ordnen Sie sie den geschriebenen Brüchen zu. drei Achtel • fünf Drittel • sieben Einunddreißigstel • ein Halb • fünf Halbe • drei Viertel • ein Zwanzigstel 1) ¾ drei Viertel 5) 1⁄20 ____________ _________________ 6) ⅜ ____________ 7) 5⁄3 ____________ 2) 5⁄2 ____________ 3) ½ ____________ 4) 7⁄31 ____________ 6b. Ergänzen Sie nun die Regel für die Aussprache von Brüchen mit den folgenden Begriffen. 3 • -stel • 2 • -tel Bei 4-19 (104-119, 204-219...) hängt man an die Zahl das Suffix________ Bei 20-100 (120-200...) hängt man an die Zahl das Suffix _______ Ausnahme:________ spricht man „Halb(e)" und _________spricht man „Drittel". 6c. Schreiben Sie die folgenden Brüche mit Hilfe der Regel auf. Text 2 Mathematik —Rechnen mit natürlichen Zahlen Vorübungen 1. Ordnen Sie die Synonyme den Begriffen zu. -r Bereich • einfach • -s Ergebnis • eventuell • -e Regel • -e Verknüpfung • vertauschen • -e Umkehrung 1) elementar einfach ___________ 2) -s Gebiet __________________ 3) -r Grundsatz _______________ 4) möglicherweise, vielleicht ____ 5) -s Resultat ___________________ 6) -e Umdrehung ________________ 7) -e Verbindung _________________ 8) verwechseln __________________ Rechnen mit natürlichen Zahlen Die einfachste Rechenoperation mit natürlichen Zahlen ist die Addition. Die Subtraktion ist die Umkehrung davon. Sie sind die Rechenoperationen erster Stufe. Das Addieren nennt man auch Zusammenzählen oder Zuzählen. Die beiden Zahlen, die addiert werden, bezeichnet man als Summanden, das Ergebnis heißt Summe. Als Operationszeichen dient „+“. Zum Beispiel: 2 + 3 = 5 wird gelesen als „zwei plus drei (ist) gleich fünf bzw. „zwei und drei ergibt fünf”. Es gelten folgende elementare Rechengesetze für beliebige Zahlen x, y und z: 1) Assoziativgesetz (der Addition): (x + y) + z = x + (y + z) = x + y + z; 2) Kommutativgesetz (der Addition): x + y = y + x; 3) Das neutrale Element ist 0: x + 0 = x; 4) Das inverse Element zu x ist -x. Die Addition kann ohne Ausnahme innerhalb der Mengen der natürlichen Zahlen, der ganzen Zahlen, der rationalen Zahlen und der reellen Zahlen ausgeführt werden. Auch andere Mengen, wie die der komplexen Zahlen besitzen eine Verknüpfung, die als Addition bezeichnet wird, weil sie denselben formalen Rechenregeln genügt. Das Subtrahieren nennt man auch Wegnehmen oder Abziehen. Die Zahl, von der subtrahiert wird, heißt Minuend, die Zahl, die subtrahiert wird, heißt Subtrahend. Das Ergebnis einer Subtraktion ist der Wert der Differenz (auch Differenzwert oder auch kurz nur Differenz). Ihr Symbol ist das Groß-Delta-Zeichen ∆, das auch als Operator für die Differenzbildung benutzt wird. Als Operationszeichen dient „–“. Zum Beispiel: 4 weniger 1 ist 3 oder anders geschrieben: 4–1=3. Exakt formuliert heißt das auch: 4 minus 1 ist gleich 3. Dabei ist 4 der Minuend, 1 stellt den Subtrahenden dar, der Rechenausdruck (Term) 4–1 ist die Differenz und das Ergebnis 3 bildet den Wert der Differenz bzw. den Differenzwert. Die Menge der natürlichen Zahlen ist bezüglich der Subtraktion nicht abgeschlossen, das heißt mit der Subtraktion erzielt man eventuell (wenn der Subtrahend größer dem Minuenden ist) ein Ergebnis, das den Bereich der natürlichen Zahlen überschreitet. Zum Beispiel: 1 – 4 = -3. Die Multiplikation und die Division sind die Rechenoperationen zweiter Stufe. Als Operationszeichen dient beim Multiplizieren ein Punkt (man liest: „mal“), früher auch ein liegendes Kreuz. Die Faktoren lassen sich vertauschen, das Ergebnis heißt Produkt. Das Dividieren ist mathematisch die Umkehrung der Multiplikation. Operationszeichen der Division ist der Doppelpunkt (man liest: „(geteilt) durch“). Das Ergebnis nennt man Quotient. Das Potenzieren und das Wurzelziehen sind die Rechenoperationen dritter Stufe. Bei der Potenz unterscheiden wir die Basis oder Grundzahl der Potenz und den Exponent oder die Hochzahl der Potenz. Zum Beispiel: 53 wird gelesen als „fünf hoch drei“. Das Radizieren oder Wurzelziehen ist die Umkehrung des Potenzierens. Die Zahl, aus der man die Wurzel zieht, heißt Radikand, der Exponent heißt hier Wurzelexponent. Zum Beispiel: √35 wird gelesen als „die Wurzel aus fünfunddreißig“ und ³√35 als „die dritte Wurzel aus 35”. Leseverstehen 2. Achten Sie beim ersten Lesen des Textes auf fett gedruckte Begriffe und Formel-zeichen und ergänzen Sie danach die Tabelle mit den passenden Begriffen aus dem Text. Operationszeichen + „plus" Rechenoperation -e Subtraktion Prozess multiplizieren Ergebnis -r Quotient 3. Lesen Sie den Text beim zweiten Mal genauer und ergänzen Sie die Sätze mit Begriffen aus dem Text. 1) Das Multiplizieren und das Dividieren sind die Rechenoperationen zweiter Stufe. 2) Das nennt man auch Wegnehmen oder Abziehen. 3) Das Dividieren ist mathematisch die der Multiplikation. 4) Das ist die einfachste Rechenoperation mit natürlichen Zahlen. Das Subtrahieren ist seine Umkehrung. 5) Das Potenzieren und das Wurzelziehen sind die Rechenoperationen Stufe. 6) Das Addieren nennt man auch oder Zuzählen. 4. Ordnen Sie die folgenden Satzteile einander zu. Beispiel: 1b 1) Das Potenzieren und Wurzelziehen a) 2) Die Zahl, von der subtrahiert wird, b) 3) Die Zahlen, die addiert werden, c) 4) Das Multiplizieren und das Dividieren d) 5) Die Zahl, aus der man die Wurzel zieht, e) 6) Das Addieren und Subtrahieren f) 7) Das Dividieren ist mathematisch g) 5. Welche der folgenden Aussagen sind richtig, welche Sie die falschen Aussagen. 1) 2) 3) 4) sind die Rechenoperationen zweiter Stufe. sind die Rechenoperationen dritter Stufe. bezeichnet man als Minuend, nennt man Radikand. die Umkehrung der Multiplikation. sind die Rechenoperationen erster Stufe. nennt man Summanden, falsch? Kreuzen Sie an und korrigieren Das Multiplizieren bezeichnet man auch als Zusammenzählen oder Zuzählen. Wenn man zwei Zahlen addiert, erhält man als Resultat eine Summe. –x ist das inverse Element zu x. Wenn der Subtrahend größer als der Minuend ist, liegt das Ergebnis nicht im Bereich der 5) 6) 7) 8) natürlichen Zahlen. Subtrahend minus Minuend ist gleich Differenzwert. Das Operationszeichen der Multiplikation ist ein Doppelpunkt. Bei 53 ist 5 die Grundzahl und 3 die Hochzahl bzw. der Exponent. Bei √35 ist 35 der Wurzelexponent. Text 3 Mathematik — Differenzialrechnung Vorübungen 1. Ordnen Sie die Synonyme den Begriffen zu. approximieren • e Bezeichnung « -s Gebiet • verwandt • -r Vorgang 1) -e Benennung -e Bezeichnung __ 4) -r Prozess ____________________ 2) verbunden _________________ 5) sich nähern ___________________ 3) -r Bereich __________________ 2. Besprechen Sie mit Ihrem Nachbarn, welche der folgenden Begriffe Sie auch ohne Wörterbuch verstehen. Ordnen Sie dann mit Hilfe des Wörterbuchs die Begriffe den Definitionen zu. -e Analysis • -r Differenzialquotient • -e Linearisierung • -r Proportionalitätsfaktor • -e Tangente ein Teilgebiet der Mathematik -e Analysis Dabei wird eine nichtlineare Funktion oder Differenzialgleichung durch eine lineare Funktion oder Differenzialgleichungen angenähert. eine Gerade, die eine Kurve in einem Punkt berührt besteht zwischen zwei Größen, wenn sie sich immer im gleichen Verhältnis ändern Grundgröße der Differenzialrechnung Differenzialrechnung a. Die Differenzialrechnung ist ein Gebiet der Mathematik und ein wesentlicher Bestandteil der Analysis. Sie ist eng verwandt mit der Integralrechnung, mit der sie unter der Bezeichnung Infinitesimalrechnung zusammengefasst wird. b. Zentrales Thema der Differenzialrechnung ist die Berechnung lokaler Veränderungen von Funktionen. c. Hierzu dient die Ableitung (auch Differenzialquotient), deren geometrische Entsprechung die Tangentensteigung ist. Die Ableitung ist der Proportionalitätsfaktor zwischen verschwindend kleinen (infinitesimalen) Änderungen des Eingabewertes und den daraus resultierenden, ebenfalls infinitesimalen Änderungen des Funktionswertes. d. Existiert ein solcher Proportionalitätsfaktor, so nennt man die Funktion differenzierbar. Äquivalent wird die Ableitung in einem Punkt als diejenige lineare Abbildung definiert, die unter allen linearen Abbildungen die Änderung der Funktion lokal am besten approximiert. Entsprechend wird die Ableitung auch die Linearisierung der Funktion genannt. e. Eine der wichtigsten Anwendungen der Differenzialrechnung ist die Bestimmung von Extremwerten, meist zur Optimierung von Prozessen. Diese befinden sich unter anderem bei monotonen Funktionen am Rand des Definitionsbereichs, im Allgemeinen jedoch an den Stellen, wo die Ableitung Null ist. Eine Funktion kann einen Maximal- oder Minimalwert haben, ohne dass die Ableitung an dieser Stelle existiert. f. Eine weitere wichtige Anwendung der Differenzialrechnung besteht in der mathematischen Modellierung physikalischer Vorgänge. Wachstum, Bewegung oder Kräfte haben alle mit Ableitungen zu tun, ihre formelhafte Beschreibung muss also Differenziale enthalten. Typischerweise führt dies auf Gleichungen, in denen Ableitungen einer unbekannten Funktion auftauchen, eben genau Differenzialgleichungen. Leseverstehen 3.Ordnen Sie beim ersten Lesen die Themen den Textteilen zu. Zwei Themen passen nicht. 1) Die Bedeutung der Differenzialrechnung 2) Der Ableitungsbegriff 3) Die Differenzialrechnung unter den anderen Wissenschaften 4) Mittel zur Berechnung lokaler Veränderungen von Funktionen 5) Ableitungsregeln 6) Die Hauptaufgabe der Differenzialrechnung 7) Typen von Differenzialgleichungen 8) Wesentliches Werkzeug zur Beschreibung von Naturgesetzen 4. Ergänzen Sie das Schema mit Begriffen aus dem Text. Analysis 5. Ergänzen Sie die Tabelle mit Informationen aus dem Text. Hauptaufgabe der Differenzialrechnung Berechnung lokaler Veränderungen von Funktionen Grundbegriffe der Differenzialrechnung Anwendungsbereich der Differenzialrechnung 6. Beantworten Sie die Fragen mit Hilfe des Textes. 1) Was geschieht, wenn der Eingabewert sich ändert? 2) Wann ist eine Funktion differenzierbar? 3) Wann ist eine lineare Abbildung äquivalent? 4) An welchen Stellen ist die Ableitung Null? 7. Ergänzen Sie die Sätze mit den gegebenen Begriffen und mit Hilfe des Textes. o Ableitung • Änderungen • -e Anwendung • -e Bildung • -e Differenzialrechnung • -r Extremwert • -e Infinitesimalrechnung • -e Steigung 1) Der Grundbegriff der Differenzialrechnung ist die Ableitung einer Funktion. 2) Teilgebiet der Analysis ist . 3) Differenzial- und Integralrechnung werden auch als bezeichnet. 4) Das mathematische Kalkül zur Behandlung infinitesimal kleiner ist die Differenzialrechnung. 5) In vielen Fällen ist die Differenzialrechnung zur von mathematischen Modellen, die die Wirklichkeit abbilden, ein unverzichtbares Hilfsmittel. 6) In geometrischer Sprache ist die Ableitung eine verallgemeinerte . 7) Meistens liegt ein an Stellen vor, wo die Funktion die Richtung (Monotonie) ändert, also an den Nullstellen der Ableitung. 8) Eine weitere wichtige der Differenzialrechnung ist das Lösen von Extremwertaufgaben. Text 4 Informatik – Was ist Informatik? Vorübungen la. Kennen Sie die folgenden Geräte? -r Computer • -e Digitalkamera • -s Handy • -r Laptop • -s Notebook • -r Palm • -r PDA • -e Spielkonsole • -s schnurlose Telefon 1b. Nennen Sie die Funktionen dieser Geräte. Wählen Sie passende Beispiele für die Verarbeitung der Information aus und bilden Sie Sätze. Texte verarbeiten • Tabellenkalkulationen machen • Statistiken sammeln • sich unterhalten • Datenbanken zusammenstellen • Sprachen erlernen • Lernprogramme erarbeiten • spielen • Grafiken gestalten • Maschinen steuern • Roboter lenken • Informationen austauschen Beispiel: Mit dem Computer kann man Datenbanken zusammenstellen. 2a. Welche Begriffe assoziieren Sie mit dem Begriff „Informatik"? Finden Sie in Ihrer Gruppe mindestens fünf Assoziationen. Dabei können Sie ein Wörterbuch benutzen. Informatik 2b. Sehen Sie sich die Abbildung an. Aus welchen Wörtern wird der Begriff „Informatik" gebildet? Klären Sie die Bedeutung dieser zwei Wörter. Information Automatik 2c Wie würden Sie den Begriff „Informatik" definieren? Schreiben Sie zusammen Nachbarn eine Definition und benutzen Sie Ihre Ergebnisse aus Aufgabe 2a und 2b. mit Ihrem Was ist Informatik? Der Begriff Informatik leitet sich vom Begriff „Information" ab. Bei Informatik geht es grundsätzlich um die Erfassung, Verbreitung, Be- und Verarbeitung von Information. Dabei werden hauptsächlich technische Lösungen betrachtet, die Teilaufgaben des Gesamtprozesses übernehmen oder unterstützen können. Informatik ist die Wissenschaft, Technik und Anwendung der maschinellen Verarbeitung, Speicherung und Übertragung von Information. Die Beschäftigung mit der Technik zur Verarbeitung von Informationen (Rechnertechnik, Technik des Programmierens) ist ein wichtiger Teil der Informatik. Zusätzlich spielt aber auch die Beschäftigung mit Informationen an sich eine Rolle (wo kommen sie her, wie kann man sie darstellen, wie können Menschen motiviert werden sie zu liefern, wie können Menschen damit umgehen). Hier gibt es enge Verbindungen zur Betriebswirtschaftslehre, Psychologie und Soziologie. Das Gebiet der Informatik ist sehr breit und wird deshalb in mehrere Teilgebiete untergliedert: Technische Informatik. Rechnerarchitektur. Dieser Bereich befasst sich mit der technischen Konstruktion von Computern, also mit physikalischen Komponenten wie Prozessoren, Speicherchips, mit der Konstruktion von Peripheriegeräten und Geräten zur Realisierung von Netzkomponenten, z. B. Router und Modems. Systemsoftware. Hier geht es um die Konzeption und Implementierung von Systemsoftware, d. h. Hardware-naher und anwendungsunspezifischer Software; also Software zur Steuerung der technischen Hardware. Beispiele für Systemsoftware sind Betriebssysteme, Netzsoftware, Software zur Steuerung von Verteilten Systemen (Client/Server), Shells, Windowsmanager. Praktische Informatik. Dieser Bereich befasst sich mit der Programmierung ganz allgemein. Beispiele für Themen sind Programmiersprachen, Übersetzerbau, das Vorgehen bei der Softwareentwicklung (Software Engineering). Außerdem beschäftigt sich die Praktische Informatik noch mit StandardAnwendungsprogrammen oder Middleware wie Datenbank- und Wissensbanksystemen. Theoretische Informatik. Sie befasst sich mit den theoretischen Grundlagen des Gebietes. Dazu zählen formale Sprachen, Automatentheorie, Semantik und Logik, Komplexitätsabschätzungen von Algorithmen. Angewandte Informatik. Hier geht es um den Einsatz von Rechnern in verschiedenen Anwendungsbereichen; die Lösungen können universell einsetzbar sein (z.B. Textverarbeitungssysteme oder Tabellenkalkulation) oder gezielt für einen Anwendungsbereich entwickelt werden (z. B. Flugbuchungssystem). Für manche Anwendungsbereiche haben sich spezielle Ausprägungen der Informatik herausgebildet, so genannte Informatik-Ableger, z.B. Wirtschaftsinformatik, Medizinische Informatik, Bioinformatik, Geoinformatik. Angewandte Informatik ist häufig interdisziplinär. Neben der Disziplin des Anwendungsbereichs sind meist beteiligt: Betriebswirtschaftslehre, Psychologie, Soziologie. Beispiele für anwendungsbereichsunabhängige Teilbereiche der Angewandten Informatik sind Rechnergestützte Gruppenarbeit (CSCW: Computer Supported Cooperative Work, Groupware) und Community-Support. Leseverstehen 3. Lesen Sie die ersten drei Abschnitte des Textes (bis „Soziologie"). Markieren Sie die Schlüsselwörter, die den Begriff „Informatik" definieren und vergleichen Sie diese Definition mit Ihrer Definition aus Aufgabe 2c. 4. Auf dem Gebiet der Informatik werden häufig Internationalismen gebraucht, die Sie wahrscheinlich aus ihrer Muttersprache kennen. Lesen Sie den gesamten Text und unterstreichen Sie alle Nomen aus der Fachsprache Informatik, die Sie kennen bzw. entschlüsseln können. 5. Lesen Sie den Text ein zweites Mal und füllen Sie die Tabelle mit Stichwörtern aus dem Text aus. Begriff Kurzdefinition Beispiel Informatik Rechnerarchitektur Technische Informatik Systemsoftware Praktische Informatik Theoretische Informatik Angewandte Informatik Text 5 Das Rechenwerk Vorübungen 1. Der Computer arbeitet nach dem EVA-Prinzip (Eingabe — Verarbeitung — Ausgabe). Den einzelnen Schritten dieses Arbeitsganges entsprechen verschiedene Teile des Computers. Ordnen Sie die folgenden Begriffe zu. -s CD-ROM-Laufwerk • -e Diskette • -s Diskettenlaufwerk • -r Drucker • -r Lautsprecher • -r Lightpen • e Maus • -s Mikrofon • -r Mikroprozessor • -r Monitor • -s Rechenwerk • -r Scanner • -r Speicherbereich • -e Tastatur Eingabe Verarbeitung Ausgabe Eingabe und Ausgabe Das Rechenwerk Die eigentliche Verarbeitung der Daten geschieht im Rechenwerk, auch Zentraleinheit (ZE) oder Central Processing Unit (CPU) genannt. Diese setzt sich aus verschiedenen Bauteilen zusammen: a) dem Mikroprozessor b) einem Speicherbereich c) Anschlüssen für externe Geräte, wie Tastatur, Monitor, Drucker und Diskettenlaufwerk d) einer Verbindungsschiene für die einzelnen Bauteile. Diese Verbindung wird auch als Bus bezeichnet. Die Weiterleitung der Daten von der Eingabe (Tastatur) an den Mikroprozessor, die Verarbeitung der Daten und die Weitergabe des Ergebnisses an Monitor, Drucker oder Speicher geschieht durch elektrische Signale. Diese Signale können dabei, ähnlich wie ein Lichtschalter, zwei Zustände haben: entweder es fließt ein Strom, oder es fließt kein Strom. Ordnet man diesen Zuständen die Zahlen 1 und 0 zu und baut auf dieser Grundlage ein neues Zahlensystem auf, so kann der Computer damit rechnen. Die kleinste Informationseinheit im Rechner besteht also aus einer 1 oder einer 0. Diese Einheit nennt man ein Bit (binary digit = binäre Ziffer). Bei der Darstellung von größeren Zahlen oder von Buchstaben brauchen wir natürlich mehrere Bit. Jeweils acht aufeinander folgende Bit bilden ein Datenwort, das man als Byte bezeichnet. Ein Byte kann dabei eine Zahl, ein Buchstabe oder ein Befehl für den Mikroprozessor sein. a) Der Mikroprozessor. Der Mikroprozessor ist das Kernstück des Rechenwerks und damit des gesamten Computers und kann mehrere Aufgaben bewältigen: Er führt nacheinander die Befehle aus, die ihm durch das Programm gegeben werden. Er übernimmt Daten aus dem Speicherbereich und von externen Geräten (Tastatur, Festplatte oder Diskette). Er verarbeitet diese Daten auf logischer und arithmetischer Grundlage. Er gibt das Ergebnis der Verarbeitung wieder aus und überträgt es zurück in den Speicherbereich oder zu externen Geräten (Monitor, Drucker,...). b) Der Speicherbereich. Die Speicherung der Daten geschieht ebenfalls in binärer Form. Die Kapazität des Speicherbereichs ist dabei auch ein Maß für die Leistungsfähigkeit eines Computers. Für 210 Byte = 1024 Byte Speicherplatz wird die Bezeichnung 1 Kilobyte (1 K oder 1 KB) benutzt. Dies entspricht etwa der Anzahl der Buchstaben auf einer halben Schreibmaschinenseite. Andererseits bedeutet das aber auch maximal 1024 Befehle für den Mikroprozessor. Die heute üblichen Kleincomputer haben eine Speicherkapazität von mindestens 128 Megabyte (MB). Dabei gilt: 1 MB = 1024 KB = 1024∙1024 Byte, das sind 1048 576 Byte. Eine noch größere Einheit ist das Gigabyte (GB). Hierfür gilt: 1 GB = 1024 MB = = 1 048 576 KB = 1 073 741 824 Byte. Der Speicherbereich enthält verschiedene Arten von Speichern: 1. Der ROM-Speicher (Read Only Memory), auch Festwertspeicher genannt, ist fest im Computer installiert und dient nur zum Einlesen von Daten und Programmen. Hier sind alle Funktionen gespeichert, die notwendig sind, den Computer zu starten und die ihn beispielsweise dazu veranlassen, nach dem Einschalten auf der Festplatte bzw. auf der Diskette das Betriebssystem zu suchen und zu laden. Der Inhalt dieses Speichers bleibt auch erhalten, wenn der Computer ausgeschaltet wird. 2. Der RAM-Speicher (Random Access Memory) ist der Arbeitsspeicher des Computers. In ihm kann man Daten und Programme speichern und natürlich danach auch wieder abrufen. Der Inhalt dieses Speicherbereichs wird beim Ausschalten des Computers gelöscht. Daten und Programme, die man dort gespeichert hat, muss man vor dem Ausschalten deshalb extern (Festplatte, Diskette) speichern, da sie sonst für immer verloren sind. Der RAM-Speicher setzt sich aus verschiedenen einzelnen Speichereinheiten zusammen, die man auch Register nennt. Das Hauptregister heißt dabei Akkumulator. Bei längeren Rechnungen wird noch ein Zwischenspeicher gebraucht, in dem Zwischenergebnisse gespeichert und dann an den Akkumulator weitergegeben oder bei Bedarf auf dem Monitor ausgegeben werden. c) Der Bus. Alle Bausteine des Computers, d.h. Mikroprozessor, Speicher und Anschlüsse für externe Geräte (Schnittstellen), sind durch den so genannten Bus verbunden. Dabei besteht der Bus aus drei voneinander unabhängigen Leitungsgruppen, denen unterschiedliche Aufgaben zufallen. 1. Der Datenbus überträgt Daten oder Befehle zwischen den einzelnen Bausteinen der Zentraleinheit. 2. Über den Adressbus laufen Informationen, an welcher Stelle im Speicher (Adresse) Daten gelesen oder abgelegt werden sollen. 3. Da alle Leitungen des Busses parallel an allen Bausteinen der Zentraleinheit anliegen, müssen noch Informationen transportiert werden, zwischen welchen Bausteinen die Daten laufen sollen. Diese Aufgabe übernimmt der Steuerbus. Leseverstehen 2. Überfliegen Sie den Text und achten Sie besonders auf die fett gedruckten Begriff Diskutieren Sie mit Ihrem Nachbarn: Was für eine Art von Text ist das? Woran habe Sie das erkannt? 1) Analyse eines Problems mit dem Rechenwerk 2) Beschreibung der Speicherung und Verarbeitung von Daten im Rechenwerk 3) Einfuhrungstext über Aufbau und Funktion des Rechenwerks 3. Welche Begriffe aus Aufgabe 1 finden Sie im Text wieder? Markieren Sie diese Begriffe und seine Funktionen. Haben Sie die Begriffe in Aufgabe l richtig zugeordnet? 4a. Tragen Sie die Schlüsselwörter aus dem Text in das Schema ein. Die Anfangsbuchstaben einiger Bestandteile helfen Ihnen bei der Lösung der Aufgabe. ____________ Verbindungsschiene⁄Bus ______________ R————— A————— R————— F————— Speicherbereich Anschlüsse für Geräte Rechenwerk _____________ Mikroprozessor T__________________ ___________________ D__________________ ___________________ 4b. Finden Sie im Text die Funktionen von den in 4a gefundenen Bauteilen. 5. Entscheiden Sie, ob die folgenden Aussagen richtig oder falsch sind und korrigieren Sie die falschen Aussagen. 1) Speicherbereich und Bus sind Teile des Mikroprozessors. 2) Durch elektrische Signale ist es möglich, Daten weiterzuleiten und zu verarbeiten. 3) Ein Byte entspricht einer 0 und einer 1. 4) Der Mikroprozessor erhält vom Programm Befehle, die er ausführt. 5) Der Mikroprozessor rechnet logische und arithmetische Aufgaben aus. 6. Beantworten Sie die folgenden Fragen mit Hilfe des Textes. 1) In welcher Form erfolgt die Speicherung der Daten? 2) Was entspricht einem Kilobyte? 3) Wie groß ist die Speicherkapazität heutiger Computer? 4) Welche Arten enthält der Speicherbereich? 5) Welche Aufgaben erfüllen der Daten-, der Adress- und der Steuerbus? Text 6 Programmiersprachen Vorübungen 1a. Übersetzen Sie zuerst die folgenden Begriffe mit dem Wortstamm „programm“ und verwenden Sie dabei ein Wörterbuch. -ablauf -folge -atisch Theater-aufbau Forschungs- programm -ierer Computer-ierung Partei-gemäß Grafik- -ierbar -ieren 1b. Erklären Sie nun auf Deutsch die Begriffe und bilden Sie mit ihnen Sätze. Beispiel: Mit einem Grafikprogramm kann man Bilder bearbeiten. ''l 1c. Welche Begriffe gehören in den Bereich der Informatik 2. Im Text dieser Einheit geht es um Programmiersprachen. Versuchen Sie, die folgenden Internationalismen aus dem Text ohne Wörterbuch zu verstehen. e Assemblersprache • -e Hybridsprache • maschinenorientiert • objektorientiert • problemorientiert • deklarativ • funktional • imperativ • logisch • parallel • prädikativ • prozedural Einteilung und Arten von Programmiersprachen Eine Programmiersprache ist eine künstliche, formale Sprache zur Formulierung von Arbeitsanweisungen an ein Rechnersystem (z. B. PC). Durch die Programmiersprache werden der Wortschatz (Anweisungen, Funktionen,...) und die Grammatik (Syntax dieser Anweisungen, Funktionen,...) eindeutig definiert, in der ein korrekter Programmtext zu schreiben ist. Je nach dem Grad der Maschinennähe teilt man die Sprachen in Maschinensprachen, niedere oder maschinenorientierte Programmiersprachen (Assemblersprachen) und (von der Hardware unabhängige) höhere oder problemorientierte Programmiersprachen ein. Höhere Sprachen werden mit Übersetzern in niedere Sprachen übertragen. Auf der Basis des einer Sprache zugrunde liegenden Konzepts oder Denkschemas werden die höheren Sprachen im Wesentlichen in vier Kategorien unterteilt: Bei imperativen (prozeduralen) Programmiersprachen besteht ein Programm (Programmrumpf) aus einer Abfolge von Operationen, die jeweils Daten bearbeiten. Wesentlich ist bei ihnen das Variablenkonzept, nach dem Eingabewerte in Variablen (Speicherzellen) abgelegt und dann weiterverarbeitet werden. Sie spiegeln deutlich die Architektur des Von-Neumann-Rechners wider. Zu ihnen gehören Programmiersprachen wie Ada, BASIC, C, COBOL, FORTRAN, Modula-2, PL/l und Pascal. Deklarative Programmiersprachen gehen davon aus, dass vorrangig nicht die Problemlösung, sondern das Problem beschrieben wird, das zu lösen ist. Für diese Problembeschreibung gibt es verschiedene Ansätze: Bei funktionalen Programmiersprachen besteht das Ziel darin, die Programmierung so nah wie möglich an die Formulierung mathematischer Funktionen anzunähern. Beispiele für funktionale Sprachen sind LISP und Logo. Logische (prädikative) Programmiersprachen basieren auf der Prädikatenlogik. Mit einem Programm wird beispielsweise versucht, die Richtigkeit einer Eingabe anhand vorhandener Fakten und Regeln zu überprüfen. Die bekannteste logische Programmiersprache ist Prolog. Verteilte und parallele Programmiersprachen. Diese Sprachen werden bei der Programmierung von Aufgaben für verteilte Rechner (z. B. vernetzte Arbeitsrechnersysteme) und Parallelrechner eingesetzt. In der Regel ergeben sich hierbei spezielle Probleme hinsichtlich der Kommunikation und Synchronisation, wofür in den Sprachen besondere Sprachkonstrukte vorhanden sind. Einerseits werden eigene Programmiersprachen wie Occam, Parallaxis u. a. entwickelt. Andererseits wurden konventionelle Programmiersprachen um entsprechende Konstrukte erweitert (z. B. FORTRAN, Pascal). Objektorientierte Programmiersprachen. Hier werden alle zum Problemlösen erforderlichen Informationen (Daten und Operationen) als Objekte aufgefasst (Objektorientierung!). Objekte sind gleichberechtigte, aktiv handelnde Einheiten, die miteinander kommunizieren, indem sie Botschaften senden und empfangen. Unter einer Botschaft versteht man dabei die Aufforderung an ein Objekt, eine bestimmte Aufgabe auszuführen. Jedes Objekt wird durch Attribute (Eigenschaften) charakterisiert. Diese beschreiben den Zustand des Objekts. Ein Objekt verfügt über Methoden (Operationen), mit denen es auf Botschaften reagiert. Die Methoden stellen die Schnittstelle des Objekts nach außen dar. Im Bereich der objektorientierten Programmiersprachen sind zwei Richtungen vorhanden: Rein objektorientierte Programmiersprachen wurden von vornherein mit diesem Konzept entwickelt (z. B. Smalltalk, Eiffel, Java). Hybridsprachen sind Sprachen, die um die Möglichkeiten der objektorientierten Programmiersprachen erweitert wurden, wie z. B. C++, Object Pascal, Oberon. Die Gesamtzahl der Programmiersprachen wird auf weit über 1000 geschätzt, von denen die meisten auf spezielle Problemstellungen zugeschnitten sind; weit verbreitet sind 20. Leseverstehen 3. Lesen Sie den ersten Absatz zur Definition und Einteilung von Programmiersprachen. Welche Aussagen sind richtig, welche falsch? Kreuzen Sie an und korrigieren Sie die falschen Aussagen. 1) Eine Programmiersprache ist keine natürliche Sprache. 2) Mit Hilfe der Programmiersprache gibt das Rechnersystem Arbeitsanweisungen. 3) Jede Programmiersprache besitzt einen bestimmten Wortschatz und eine bestimmte Grammatik. 4) Programmiersprachen lassen sich nach ihrer Nähe zur Maschine einteilen. 5) Problemorientierte Programmiersprachen sind in Bezug zur Hardware am unselbstständigsten. 6) Höhere Programmiersprachen übersetzen die niederen Programmiersprachen. 4. Lesen Sie den gesamten Text und unterstreichen Sie alle Programmiersprachen. Ordnen Sie diese danach den folgenden Aussagen zu. Einige Programmiersprachen müssen mehrmals in die Tabelle eingetragen werden. Programmiersprachen Beschreibung 1) Alle Informationen, die für die Lösung des Problems notwendig sind, werden als Objekte aufgefasst. 2) Objekte werden durch Attribute beschrieben und besitzen Methoden. 3) Das Programm schreitet von Operation (und der entsprechenden Bearbeitung der Daten) zu Operation voran. 4) Sie wurden nachträglich mit Merkmalen der objektorientierten Programmierung ergänzt. 5) Statt der Problemlösung wird das zu lösende Problem beschrieben. 6) Eingabewerte werden mit Variablen beschrieben und weiterverarbeitet. 7) Geeignet, um Probleme bei der Kommunikation und Synchronisation in verteilten Rechnern und Parallelrechnern zu lösen. 8) Basis ist die Prädikatenlogik. 9) Sie wurden von Anfang an nach dem Prinzip der Objektorientierung entwickelt. 10) Es wird versucht, mathematische Funktionen zu formulieren. 5. Beantworten Sie die folgenden Fragen mit Hilfe des Textes. 1. Wie funktioniert das Variablenkonzept? 2. Was bedeuten die Begriffe Objekt, Botschaft, Attribut und Methode? 3. Worin unterscheiden sich rein objektorientierte Programmiersprachen von Hybridsprachen? Text 7 Rechnernetze Vorübungen 1. Welche Form haben die Zeichnungen? Beschreiben Sie sie mit Hilfe der folgenden Begriffe. -r Knoten • -e Linie • -r Ring • -r Stern • verbunden sein mit • sich verzweigen in Das Rechnernetz Ein Rechnernetz ist ein räumlich verteiltes System Datenübertragungseinrichtungen miteinander verbunden sind. von Rechnern, die durch Die Kommunikation erfolgt über verschiedene Protokolle, die mittels des ISO/OSI-Modells strukturiert werden können. Hier werden aus kleinen grundlegenden Strukturen durch Verknüpfung größere und komplexere Strukturen gebildet. Dabei greifen höhere (komplexere) Protokollschichten auf die Funktionalitäten von einfacheren darunter liegenden Protokollschichten zu. Ein wichtiges Prinzip dabei ist, dass man den meisten Protokollschichten (Nutz-)Daten (Payload) zum Transport übergeben kann. Die Protokollschicht fügt zu diesen Nutzdaten (deren Inhalt sie weitgehend ignoriert) vorne und teilweise hinten weitere Daten an, die für den Transport durch die Protokollschicht wichtig sind. Jedoch gibt es auch hiervon Ausnahmen, da einige Protokolle nicht dazu gedacht sind, fremde Nutzdaten zu transportieren, sondern ausschließlich als eigenständige Informationssysteme für bestimmte Aufgaben fungieren. Unter der Topologie versteht man die Art, wie die verschiedenen beteiligten Komponenten (also zumeist Rechner) im Netz durch physische oder logische Leitungswege verbunden sind. Man bildet Rechnernetze, in denen es Verbindungen und Knoten gibt, über die man gegebenenfalls über mehrere Zwischenpunkte von jedem Bereich des Netzes zu jedem anderen Bereich des Netzes kommen kann. Bei der Stern-Topologie sind an einen zentralen Verteilpunkt alle anderen Teilnehmer mit einer Zweipunktverbindung angeschlossen. Ein Ausfall des zentralen Verteilpunktes bewirkt den Ausfall aller Verbindungsmöglichkeiten zur gleichen Zeit. Diese Topologie wird eigentlich nur in Kleinstnetzen (häufig bei LAN-Partys) verwendet. Bei der Baum-Topologie verbindet man mehrere Netze der Sterntypologie hierarchisch miteinander. Von der obersten „Wurzel" (der erste bzw. oberste Rechner) gehen Kanten (Links) aus, die zu einem Endknoten oder der Wurzel (Verteiler) weiterer Bäume führen. Der Ausfall eines Endgerätes hat zwar keine Folgen, aber bei Ausfall eines Verteilers ist der ganze davon ausgehende (Unter)Baum „tot". Bei der Ring-Topologie werden jeweils zwei Teilnehmer über Zweipunktverbindungen miteinander verbunden, so dass ein geschlossener Ring entsteht. Die zu übertragende Information wird von Teilnehmer zu Teilnehmer weitergeleitet, bis sie ihren Bestimmungsort erreicht. Fällt ein Teilnehmer aus, bricht das gesamte Netz zusammen, es sei denn, die Teilnehmer beherrschen Protection-Umschaltung. Eine Sonderform der Ringtopologie ist die Linien-Topologie, bei der es sich um einen „offenen Ring" handelt, d. h. der erste und der letzte Rechner sind nicht miteinander verbunden. Eine Bus-Topologie besteht aus einem Hauptkabel, dem Bus, an das alle Geräte und zwei Endwiderstände angeschlossen sind. Vorteile sind der geringe Kabelbedarf und die Unabhängigkeit von der Funktion einzelner Endgeräte: Bei einem Ausfall eines Knotens oder eines Endgerätes bleibt das gesamte System trotzdem intakt. Größte Gefahr ist jedoch ein Kabelbruch im Hauptkabel, durch den der ganze Bus ausfällt. In einem vermaschten Netz ist jedes Endgerät mit einem oder mehreren anderen Endgeräten verbunden. Wenn jeder Teilnehmer mit jedem anderen Teilnehmer verbunden ist, spricht man von einem vollständig vermaschten Netz. Bei Ausfall eines Endgerätes oder einer Leitung ist es im Regelfall möglich, durch Umleiten (Routing) der Daten weiter zu kommunizieren. Leseverstehen 2. Beantworten Sie die Fragen. 1) Wie sind die Protokolle strukturiert? 2) Wie werden die (Nutz)Daten durch die Protokollschichten transportiert? 3) Was ist eine Topologie? 3. Ordnen Sie die im Text genannten Topologien den Zeichnungen aus Aufgabe l zu. 4a. Füllen Sie die Tabelle mit dem Aufbau und den Vor- und Nachteilen der einzelnen Topologien mit Stichwörtern aus dem Text aus. Topologie Aufbau Vorteile Nachteile Stern-Topologie Baum-Topologie Ring-Topologie Linien-Topologie Bus-Topologie Vermaschtes Netz 4b. Suchen Sie im Internet nach weiteren Vor- und Nachteilen und ergänzen Sie die Tabelle.