2013 Round 2 with Key

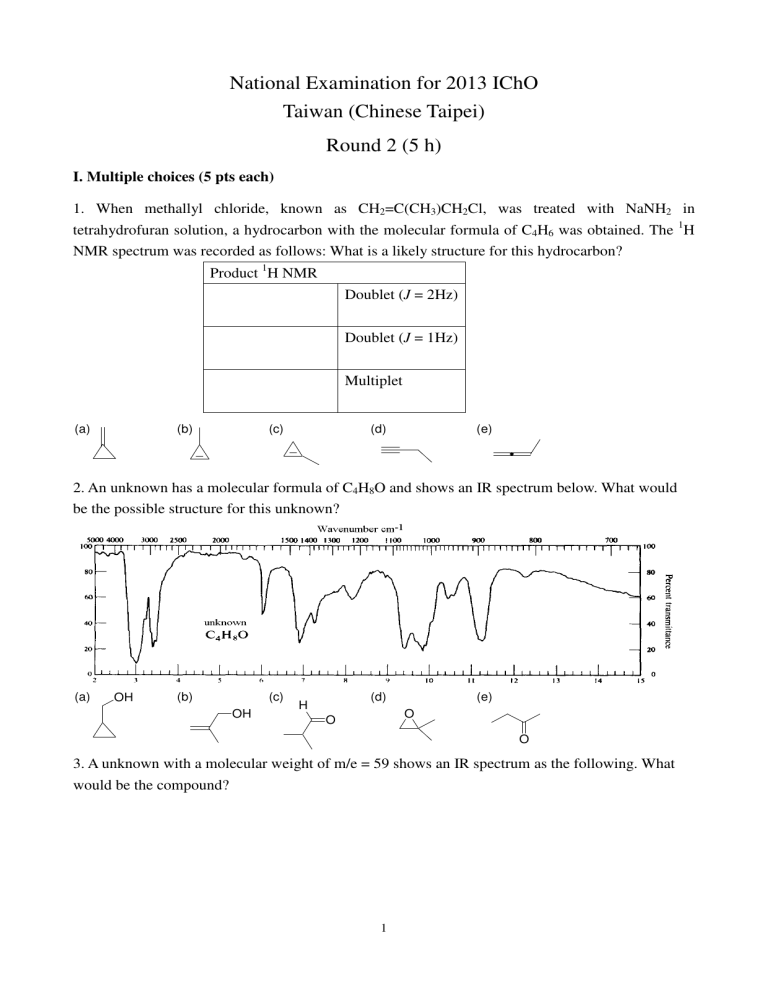
National Examination for 2013 IChO
Taiwan (Chinese Taipei)
Round 2 (5 h)
I. Multiple choices (5 pts each)
1. When methallyl chloride, known as CH2=C(CH3)CH2Cl, was treated with NaNH2 in
tetrahydrofuran solution, a hydrocarbon with the molecular formula of C4H6 was obtained. The 1H
NMR spectrum was recorded as follows: What is a likely structure for this hydrocarbon?
Product 1H NMR


Doublet (J = 2Hz)


Doublet (J = 1Hz)

Multiplet

(a)
(b)
(c)
(d)
(e)
2. An unknown has a molecular formula of C4H8O and shows an IR spectrum below. What would
be the possible structure for this unknown?
(a)
OH
(b)
(c)
OH
(d)
H
(e)
O
O
O
3. A unknown with a molecular weight of m/e = 59 shows an IR spectrum as the following. What
would be the compound?
1
(a)
NH2
(b)
OH
(c)
(d)
N
H
O
H
(e)
O
NH2
NH2
Answer questions 4-6 about the study of [14]annulene.
Following scheme shows the preparation of [14]annulene P from Q. Under basic conditions, Q was
first converted to I as an intermediate that would further cyclize to form P, a [14]annulene.
BF4H3C S
CH3
10
8
11
6
9
KOtBu
R H3C
R H3C
4
7
2
5
CH3
3
S CH3
H3C BF4
R = (CH2)10CH3
1
R = (CH2)10CH3
Q
I
P, [14]Annulene
4. What is the function of KOtBu in the first step?
(a) An oxidizing agent to oxidize the –S(CH3)2+ group
(b) A Lewis acid to promote the elimination
(c)
(d)
(e)
A reducing agent to reduce the –S(CH3)2+ group
A base to promote the elimination
A nucleophile to promote the elimination
5. Anti and syn are two possible stereoisomers for I. The 1H NMR was partially resolved. The
olefinic proton signals at  6.32 and 6.35, and benzylic methyl (ArCH3) at  1.53 were
identified. Which of the following statement about the structural assignment of I is correct?
(CH2)10CH3
(CH2)10CH3
H3C
CH3
Anti
Syn
(a)
(b)
(c)
I is anti because the benzylic methyl shows a shielded singlet in the NMR
I is anti because there are two sets of non-equivalent olefinic proton in the NMR
I is syn because the benzylic methyl shows a shielded singlet in the NMR
(d)
(e)
I is syn because there are two sets of non-equivalent olefinic proton in the NMR
The stereochemistry of I cannot be identified according to the above information
2
6. Assign the proton chemical shifts for H(1), H(3), H(7) and H(10) in P. The  values are -4.02,
-0.41, 0.97, 1.20.
(a) The assignments are  1.20, 0.97, -0.41, -4.02 for H(1), H(3), H(7) and H(10)
respectively
(b) The assignments are  1.20, -0.41, 0.97, -4.02 for H(1), H(3), H(7) and H(10)
respectively
(c) The assignments are -4.02, -0.41, 1.20, 0.97 for H(1), H(3), H(7) and H(10)
respectively
(d) The assignments are -0.41, -4.02, 0.97, 1.20 for H(1), H(3), H(7) and H(10)
respectively
(e) The assignments are -4.02, -0.41, 0.97, 1.20 for H(1), H(3), H(7) and H(10)
respectively
3
II. Problems
1. Draw the structural formula of each of the following isomers with a formula of C20H18O. (20
pts)
Isomer A (5 pts)


Isomer B (5 pts)


singlet


doublet (J = 7 Hz)


singlet

doublet (J = 7 Hz)

broad peak

2.



singlet


singlet
(a) Provide the structure of the product (3 pts, no need to show stereochemistry). (b) Label the
absolute stereochemistry of the carbon center in the starting material (shown by arrow) (3 pts)
OH OH
O
H+
R
R'
CH3
3.
?
HO CH 3
benzene
Dear-Stark trap
Provide suitable reagents for each reaction step. (4 pts each, total 12 pts)
OH
O
?
N
O
H
S
NH
?
?
S
4.
singlet
S
S
Provide suitable reagents or product structure for each reaction step. (4 pts each, total 12 pts)
O
H
?
O
?
OH
O
OH
5.
OH
OH
Oder the following acids with increasing acidity. (4 points)
4
H+
benzene
Dear-Stark trap
?
OH
Cl
O
OH
OH
O
6.
O
O
O
(a) Which of the following compounds exist as hydrates in water? (3 pts) (b) Show the
structure of the hydrates. (3 points)
O
H
7.
OH
OH
H
O
N
OH
Cl3C
CCl3
H
N
N
H
H
N
H
O
H
Cl3C
O
O
H
H 3CO
OCH 3
Cl3 CO
O
OCCl3
H
H
Lily aldehydes, used in perfumes, can be made starting with a mixed aldol condensation
between two different aldehydes.
Provide their structures. (4 points)
O
H
lily aldehyde
8.
.
Vitamin B6 (an aldehydes) reacts with an enzyme (partial structure shown below) to form a
coenzyme that catalyzes the conversion of -amino acids to -keto acids.
O
-
O P O
O
H
CHO
+ H 2N enzyme
N
coenzyme
OH
CH 3
(1) Provide the structure of the coenzyme. (2 points)
(2) -Amino acids have the general structure shown below. Provide the structure of an a-keto
acid. (2 points)
CO 2H
H 2N
R
α-amino acid
9. Considering bromobutane reaction: (4 pts each, total 28)
(a) Write equations for the substitution reactions of 1-bromobutane and (S)-2-bromobutane with
the following reagents:
5
(1) CH3COONa
(2) NaCN
(b) Write the rate law for the substitution reactions of 1-bromobutane with NaN3
(c) Draw the reaction energy diagram for the substitution reaction of (S)-2-bromobutane with
KOH
(d) Draw the transition state structure for the substitution reaction of (S)-2-bromobutane with
KOH
10. Phenanthrene can undergo the following reaction: (4 pts each, total 20)
OsO4 (cat.)
oxidant
OH
OH
(a) Write equations for the reactions of phenanthrene with the following reagents:
(1) Br2
(2) mCPBA
(b) Write the equation for the bromination of benzene
(c) Draw the reaction energy diagram for the bromination of benzene
(d) Draw the possible product(s) for the bromination of naphtalene
11. Determine whether each of the following compounds is optically active (Chiral) or optically
inactive (achiral). (1 pt each)
6
7
12. What is the % of the R enantiomer in a sample of carvone that has a specific rotation of 30,
given that the specific rotation of R-carvone is -61? (3 points)
13. Draw the element symbols for A, B, C, and D. (4 points)
14. Assign the following stereocenter as R or S. (14 pts)
(a)
(b)
(c)
15. Calculate the specific rotation of the following sample taken at 25 oC using the sodium D line.
1.00 g of sample is dissolved in 20.0 mL of ethanol. 5.0 mL of this solution is placed in a
20.0-cm polarimeter tube. The observed rotation is 1.25o counterclockwise. (3 points)
8
16. For each of the following pairs of compounds, determine the relationships between the two
compounds: (18 points)
A. Enantiomers
B. Diastereomers
C. Structural Isomers
D. Identical
9
17. A tetracoordinated complex Mabcd is known to have stereoisomers. Please draw the 3-D
structures for all the possible stereoisomers. (M stands for the central metal ion and a, b, c, and d
each stand for a monodentate ligand) (10%)
18. Please explain the d orbital energy splitting diagrams for the tetrahedral and octahedral
complexes. (10%)
19. Draw and mark the symbols (∆ and Λ) for the enatiomers of Cr(acac)3. (10%)
20. The magnetic moment of [Mn(en)2Br(NO)]+ is 6.06  B (B.M.)
Answer the following questions (20%):
(a) How many lone pair electrons does the central Mn ion have?
(b) Draw the d-orbital energy splitting diagram for the Mn ion.
(c) What is the oxidation state of the Mn ion?
(d) Draw all stereoisomers for [Mn(en)2Br(NO)]+.
21. Ionization energies should depend on the effective nuclear charge that holds the electrons in the
atom. Calculate the effective nuclear charge Z* (Slater’s rules) for N, P, and As. Do their
ionization energies seem to match these effective nuclear charges? If not, what other factors
influence the ionization energies? (15 pts)
22. The electron configuration of a chromium atom is [Ar]4s13d5 rather than [Ar]4s23d4. Five d
electrons could have five unpaired electrons or one unpaired electron as shown below. Which
arrangement is likely to have lower energy? (10 pts)
23. Two isomers having the formula N2CO are known: ONCN and ONNC. Draw the most
important three resonance structures of these isomers, and determine the formal charges. Which
isomers do you predict to be the most stable (lowest energy) form?
(15 pts)
24. Use the following data to determine the half-life (t½) of and the rate constant (k) for the decay
of
.
(10 pts)
Time/s
0
Moles
0.250
200
400
600
800
1000
0.110
0.057
0.025
0.012
0.005
10
25. A 40.0 mL solution of 0.040M Hg2(NO3)2 was titrated 0.10 M KI to precipitate Hg2I2 (Ksp =
1.1× 10-28).
(a) What volume of KI is needed to reach the equivalence point? (6 pts)
(b) Calculate the ionic strength of the solution when 60.0 mL of KI have been added. (6 pts)
(c) Using activities, calculate pHg22+ (= -log(activity)) for (b) (8 pts)
(ion size α: Hg22+ =400 nm, I-=300 nm)
26. A solution contains 0.10 M Ce3+, 1.0×10-4M Ce4+, 1.0×10-4M Mn2+, 0.1 M MnO4- and 1.00M
HClO4. (standard reduction potential (E0)for Ce4+ Ce3+ = 1.70V , MnO4- Mn2+ = 1.507V)
(a) Write a balanced net reaction that can occur between the species in the solution. (6 pts)
(b) Calculate E for the conditions given. (6 pts)
(c) At what pH would the given concentrations of Ce3+, Ce4+, Mn2+, MnO4- be in equilibrium at
298 K. (6 pts)
27. Please describe the working principle and structure detail of pH measurement glass electrode.
(12 pts)
28. Differentiate between the equivalence point & the end point of a titration. (12 pts)
29. Describe how you determine the pKa of specific weak acid through titration. (For example,
how to determine the pKa of acetic acid.) (10 pts)
30. Sulfuric acid is usually in that one of its protons behaves as a strong acid and the other as a
weak acid (Ka2 = 1.02 × 10-2). As an example, consider how the hydronium ion concentration
of sulfuric acid solutions is computed using a 0.00500 M solution. (16 pts)
31. Describe how to prepare approximately 500 mL of pH 5.0 buffer solution from a 2.0 M acetic
acid (HOAc) and sodium acetate (NaOAc). (12 pts)
32. The decomposition of N2O5(g) to form NO2(g) and O2(g) is a first-order reaction. A certain
amount of N2O5(g) is placed in a 5.00-L closed vessel and allowed to decompose at 330 K. The
rate of appearance of the red-brown NO2(g) is 9.60 × 10-5 mol⋅L-1⋅s-1 at t = 0 and 2.40 × 10-5
mol⋅L-1⋅s-1 at t = 1386 s, respectively. The standard enthalpy of reaction (∆H°) is 195 kJ per
mole of N2O5(g). Answer the following questions. (R = 0.0821 L⋅atm⋅K-1 = 8.314 J⋅K-1)
(A) Write a balanced chemical equation (with the smallest integer of coefficients) for the reactions.
(B) Draw the Lewis structure of N2O5 molecule (show any one of the resonance structures)
(C) Find the half-life and the rate constant for the decomposition of N2O5.
11
(D) Find the initial pressure of N2O5(g).
(E) Find the enthalpy of reaction after 1386 s.
(F) Give an expression for the total pressure in the closed vessel as a function of time.
(G) Estimate the bond energy of N−O, given that the bond energy of O=O is 498 kJ/mol.
(H) If the decomposition of N2O5(g) is carried out at 340 K, the initial rate for the appearance of
NO2(g) is 9.60 × 10-4 mol⋅L-1⋅s-1. Find the activation energy of the reaction.
33. For the hydrogen atom, the solutions of the Schrodinger equation, are typically labeled by three
quantum numbers: n,l,ml. These wavefunctions,
Consider the following wavefunction:
ψ n ,l , m
l
1/ 2
 1 

ψ n ,l ,ml (r ,θ , φ ) = 
3 
 32πa0 
(2 −
, are also called the atomic orbitals.
r −r / 2 a0
)e
a0
(a) Which atomic orbital is this? (2pts)
(b) What is the value for the quantum numbers n, l, ml for this orbital? (3pts)
(c) How many nodes are there in this atomic orbital? Indicate the position of the node(s) in terms of
a0. (3pts)
(d) Draw the shape of this orbital, label the phase and the node(s) clearly. (2pts)
34. The particle in a 1D box provides a crude model for π electrons in linear conjugated
hydrocarbons. The general formula for the energy and wavefunctions of one dimensional
particle in a box are:
1/ 2
n2h2
2

 nπx 
En =
n = 1, 2, ...
ψ n ( x) =   sin 
 n = 1, 2, ...
2
8mL
L
 L 
In the following, we will consider the electronic structure of the π electrons in butadiene,
CH2=CH-CH=CH2.
(a) Consider two conditions for the π electrons in butadiene (a) the two pairs of π electrons are
localized on their respective C=C double bonds, and (b) all four π electrons can move freely on
the four carbon atoms. According to the 1D particle in a box model, what is the total energy
difference between the two situations? Which one is more stabilized? (Estimate the length of the
box with the following C-C bond lengths: C-C ~ 154pm, C=C ~ 134pm.)
12
(b) Experimentally, butadiene has an absorption band that peaks at λ = 217 nm. According to your
choice in (1) (the more stabilized situation), what is the longest absorption wavelength for
butadiene ?
(c) Write a general formula for the energy gap between the highest occupied state and the lowest
unoccupied state of N-polyenes (e.g. N=2 for butadiene, and N=3 for hexatriene).
(d) Molecules with a long conjugated hydrocarbon chain show a strong color and are called
pigments, e.g. , beta-carotene shows a strong orange color.
Why?
Beta-carotene
35. An ideal gas consists of 1mol of diatomic molecules that rotate but do not oscillate. The
molecular diameter is 250 pm. The gas is expanded reversibly at a constant pressure of 2.0x105
Pa, with a transfer of 70 J as heat. What is the change in the mean free path of the molecules?
36. In an industrial process the volume of 1.0 mol of a diatomic ideal gas is reduced at a uniform
rate from 0.616 m3 to 0.308 m3 in 2.00 h while its temperature is increased at a uniform rate
from 27.0°C to 450°C. Throughout the process, the gas passes through thermodynamic
equilibrium states.
What are (a) the cumulative work done on the gas, (b) the cumulative energy absorbed by the
gas as heat.
(R=8.314 J/(mol K))
13
National Examination for 2013 IChO
Taiwan (Chinese Taipei)
Round 2 (5 h)
I. Multiple choices (5 pts each)
1
2
3
4
5
6
(c)
(b)
(e)
(d)
(a)
(e)
II. Problems
(b) (10pts)
1. (a) (10 pts)
H
OH
H
OH
H
H
A
B
(b) (3 pts)
2. (a) (3 pts)
(S)
3. (a) (4 pts)
(c) (4 pts)
(b) (4 pts)
NH2NH2
MgBr ,
THF
N
ClCrO 3-
H
,
PCC
14
(b) (4 pts)
4. (a) (4 pts)
LiAlH4
(c) (4 pts)
1) O3
2) (CH3)2S
O
O
H
5. (4 pts)
OH
OH
OH <
<
O
OH
OH
O
2.50
4 pts
Cl
O
O
O
O
2.83
OH <
<
OH
OH <
O
3.08
4.87
pKa:
O
Cl
OH
<
OH
O
O
partial credit, 2 pts
wrong
6. (a) (3 pts)
(b) (3 pts)
O
Cl3C
HO OH
H
Cl3 C
H
O
H
HO OH
H
H
7. (4 pts)
CHO
+
O
H
15
1
H
(b) (3 pts)
8. (a) (3 pts)
HO
CO 2H
N
H
N
enzyme
O
R
OH
CH 3
9. (a) (4 pts each，total 28 pts)
(i)
(ii)
(b)
(c)
(d)
R = k[1-bromobutane][MaN3]
16
10. (a) (每格 4 pts，共 20 pts)
(ii)
(i)
No or wrong Stereochemistry
- 2 pts
(b)
(d)
(c)
11. (Code only) (10 pts)
(b), (g), (j)
12. (3 pts)
If R-carvone fraction is R,
-61(R) + 61(1-R) = 30
R = 0.254
R-carvone is 25.4%
13. (1 pts)
A= H
(1 pts)
B=H
(1 pts)
C = Br
(1 pts)
D = Br
OR (A = Br)
(B = Br)
(C = H)
(D = H)
14. (a) (1 pt each，total 4 pts)
(b) (1 pt each，total 5 pts)
(c) (1 pt each，total 5 pts)
1
2
3
4
1
2
3
4
5
1
2
3
4
5
R
R
R
R
R
S
S
R
R
S
R
S
R
R
17
15. (3 pts)
 = -1.25/(1/20)x(2) = -12.5
16. CODE: A. Enantiomers
(1 pt each，total18 pts)
B. Diastereomers
C. Structural Isomers
D. Identical
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
B
B
A
D
A
A
A
B
A
(j)
(k)
(l)
(m)
(n)
(o)
(p)
(q)
(r)
D
A
B
D
C
B
B
D
A
17. (10 pts)
18. (10 pts) Tetrahedral
Octahydral
18
19. (10 pts)
20. (20 pts)
(a)
N = 5, Mn has 5 unpaired electrons.
(b) [Mn(en)2Br(NO)]+ is 6-coordinat, therefore, is an octahedral complex.
(c)
Since Mn is d5，it oxidation number is +2.
(d) three isomers:
19
21. (15 pts)
N: Z* = 7 – (2 × 0.85 + 4 × 0.35) = 3.90
IE = 1.402 MJ/mol r = 0.75 Å
P: Z* = 15 – (2 × 1 + 8 × 0.85 + 4 × 0.35) = 4.80
IE = 1.012 MJ/mol r = 1.06 Å
As: Z* = 33 – (2 × 1 + 8 × 1 + 18 × 0.85 + 4 × 0.35) = 6.30 IE = 0.947 MJ/mol r = 1.06 Å
The effect of shielding alone is not sufficient to explain the changes in ionization energy. The
other major factor is distance between the electron and the nucleus. The term Z*/r2 correlates
better, but As is still out of order.
radius (Å)
Z*/r2
N 0.75
6.93
P 1.06
As 1.20
4.27
4.38
22. (10 pts)
This configuration has 10 exchange possibilities, energy
contribution 10 Πe..
This configuration has two pairs, Coulombic energy contribution
2Πc. In addition, this configuration has 4 exchange possibilities,
energy contribution 4 Πe. Overall, 2Πc + 4 Πe.
Because Πc is positive and Πe is negative, the energy of the half-filled arrangement is accordingly
lower than that with two pairs of electrons.
23. (15 pts)
ONCN
ONNC
Structure ONCN-II is the best by the formal charge criterion, with no formal charge, and is
expected to be the most stable.
24.
-1
(10 pts)
Plot ln[P0] vs t. Get slope of 0.0039 s-1 which is -k.
we get t½ = 178 s.
-2
ln[Po]
-3
-4
-5
-6
0
200
400
600
800
1000
time/s
20
t½ = ln2/k
25. (a) (6 pts)
moles of I- = 2 (moles of Hg22+)
(Ve)(0.1M) = 2 (40 mL) (0.04M),
Ve= 32 mL
(b) (6 pts)
Virtually all Hg22+ precipitated, 3.2 mmol I- precipitated
[NO3-] = 0.032 M, [I-]=0.028 M, [K+]=0.06 M
µ= 1/2 (ΣCi Zi2)= 0.06M
(c) (8 pts)
I- , log γ= ( -0.1249/1.241)= -0.1007, γ=0.793
activity (Hg22+)= Ksp / activity(I-)2 = 1.1×10-28/(0.028)2(0.795)2 = 2.2×10-25
-log(activity Hg22+)=24.65
26. (a) (6 pts)
5Ce4++ Mn2+ + 4H2O 5Ce3+ + MnO4- + 8 H+
, E0= 0.193V
(b) (6 pts)


0.05916
[Ce3+ ]5  
0.05916
[ Mn2 + ]

 = −0.02V

E = 1.70 −
log
−
1
.
507
−
log
4+ 5 
−
+ 8 

5
[Ce ]  
5
[ MnO4 ][ H ] 

(c) (6 pts)
at equilibrium, E=0,
E0 =
0.0591 [Ce3+ ]5[ MnO4− ][ H + ]8
log
5
[Ce4 + ]5[ Mn2 + ]
[H+] = 0.62 , pH=0.21
pts)
27. (12
28. (12 pts)
Titration equivalent point in a theoretical point, that the amount of standard titration reagent
solution is exactly equal to the amount to be detected.
Titration end point occurs when the state of the physical change point, usually the indicator
changes color according to the moment of termination of the titration point, called the end.
21
29. (10 pts)
+
[H + ][CH3COO− ]
Ka =
[CH3COOH]
−
CH3COOH ⇔ H + CH3COO
At half-equivalent point, [CH3COOH] = [CH3COO¯ ], so Ka = [H+], pKa = pH
30. (16 pts)
[H3O+] ≈ [HSO4－] ≈ 0.00500
2-
0.00500 [SO 4 ]
=1.02 × 10-2
0.00500
+
[H3O ] = 0.00500 + [SO42-]
1
[SO42-] = [H3O+]–0.00500……○
According to mass conservation law:
－
2
CH2SO4 = 0.00500 = [SO42-] + [HSO4 ]…….○
1 and ○
2 :
Combine ○
－] = 0.01000–[H O+]
[HSO4
3
[H 3 O + ]([H 3 O + ] - 0.00500)
=1.02 × 10-2
0.01000 - [H 3 O + ]
[H3O+]2 + 0.0052[H3O+]–1.02 × 10-4 = 0
[H3O+] = 7.83 × 10-3M
31. (12 pts)
Ka = 1 .75 * 10 −5
HOAc → H + + OAc −
[H ][OAc ] = 1.75 * 10
+
Ka =
−
−5
[HOAc ]
[HOAc ] = 2 M
[
⇒ OAc
−
=
10
−5
[
* OAc
[HOAc ]
[H ] = 10
[OAc ] = 1.75
pH = 5
−
]⇒
+
−
[HOAc ]
] = 3 .5 M
3 .5 * 0 .5( L ) * 82 .034 = 143 .69 g
32. (a) (3 pts)
2 N2O5 → 4 NO2 + O2
(b) (3 pts)
22
−5
M
(c) (4 pts)
d [ NO 2 ]
d [ N 2 O5 ] R
; −
R=
= = k[ N 2O5 ] ;
dt
dt
2
[ N 2O 5 ]t Rt / 2 1.20 ×10 −5 1
=
=
=
[ N 2O 5 ]o Ro / 2 4.80 ×10 −5 4
after 2 half-lives
2 × t1/2 = 1386 s; t1/2 = 693 s; k =
0.693
= 1.00 ×10 −3 s −1
t1/ 2
(d) (4 pts)
Ro / 2 4.80 × 10 −5
=
= 0.0480 mol ⋅ L−1 ;
−3
k
1.00 × 10
Po = [N2O5]oRT = 0.0480 × 0.0821 × 330 = 1.30 atm
[ N 2 O 5 ]o =
(e) (4 pts)
 1
∆H = 195 × 0.0480 × 5.00 × 1 −  = 70.1 kJ
 4
(f) (4 pts)
[
]
(
)
P = Po e − kt + 2(1 − e − kt ) + 0.5(1 − e − kt ) = Po 2.5 − 1.5e − kt ; Po = 1.30 atm
& k = 1.00 × 10-3 s-1
(g) (4 pts)
4 moles of N−O bonds are broken and 1 mole of O=O bond is formed in the reaction, thus
4 BE(N−O) – BE(O=O) = 195 × 2; BE(N−O) = 222 kJ/mol
(h) (4 pts)
R  E 1 1 
 9.6 ×10 −4  Ea  1
1 
-1
=
ln 2  = a  −  ; ln
−

 ; Ea = 215 kJ⋅mol
−5 
 9.6 × 10  R  330 340 
 R1  R  T1 T2 
(b) (3 pts)
33. (a) (2 pts)
This wavefunction have no
n=2, l=0, ml=0
angular part, therefore, it is a
spherical symmetrical orbital.
There is one nodal plane on the
(c) (3 pts)
One spherical nodal plane
reside on r=2a0.
radial part makes it 2s orbital.
23
(d) (2 pts)
34. (a) (8 pts)
For (i)
for (ii)
L = 134 ×10
−12
m, Etotal
12 h 2
=4
= 1.34 ×10-17 J
2
8mL
L = (2 × 134 + 154) × 10 −12 m, Etotal = 2
(12 + 2 2 ) h 2
= 3.38 ×10 -18 J
8mL2
System (ii)is about 10-18 J lower than system (i).
(b) (5 pts)
(32 − 2 2 )h 2
c
c8mL2
= h ,λ =
= 1.17 × 10 −7 m = 117 nm
2
8mL
5h
λ
(c) (7 pts)
Box length for N straight double-bond unit is L=(2N-1)l
highest occupied state, HOS, is
E HOS
lowest unoccupied state, LUS, is
difference:
(d) (5 pts)
N 2h 2
=
8mL2
ELUS =
∆E = E LUS − EHOS =
( N + 1) 2 h 2
8mL2
(2 N + 1)h 2
h2 2N + 1
=
8m(2 N − 1) 2 l 2 8ml 2 (2 N − 1) 2
h 2 2 × 11 + 1
c
∆E =
=h
2
2
λ
8ml ( 2 ×11 − 1)
c8ml 2 212
λ=
~ 1312nm
h 23
24
35. (15 pts)
Molar heat capacity for diatomic molecule:
5
7
C p = Cv + R = Cvtrans + Cvrot + R = R + R = R
2
2
The enthalpy change for constant pressure expansion:
∆H = C p ∆T =
7
R∆T
2
Internal energy change:
∆E = ∆H − ∆(PV ) = ∆H − R∆T =
7
5
R∆T − R∆T = R∆T
2
2
Ideal gas law:
P∆V = R∆T
5
We get: ∆E = P∆V
2
（1）
By the first law of thermodynamics:
V2
∆E = q − ∫ Pext dV
V1
= q − Pext ∆V
70J − P∆V
= 90
（2）
From eq (1)and (2), we get:
2
20J
P∆V = ⋅ 70J = 20J , ∆V =
= 1.0 × 10 −4 m3
7
2.0 × 10 5 Pa
mean free path： λ =
1
1
=
V
2
2πd N /V
2 πd 2 N
the change of mean free path is:
1
1
λ2 − λ1 =
∆V =
1.0 × 10 −4 = 5.98 × 10 −10 m
2
2
−10
23
2πd N
2π (2.5 × 10 ) ⋅ 6.02 × 10
25
36. (a) (10 pts)
The system is in equilibrium at all times, therefore, Pext = P
w = − ∫V Pext dV = − ∫V PdV
V2
V2
1
1
For ideal gas: P =
w = −nR ∫V
V2
1
nRT
V
T
dV
V
for further calculation, we need derive the relationship between T and V.
When 0 < t < 2 , we have
V (t ) = 0.616 +
0.308 − 0.616
t
2
T (t ) = 273 + 27 +
= 300 +
450 − 27
t
2
450 − 27
t
2
we get:
450 − 27 V − 0.616
×
2
−0.154
3
= 300 −1.373 × 10 (V − 0.616)
T (t ) = 300 +
= 1146 −1.373 × 10 3 V
3
0.3081146 −1.373 × 10 V
w = −R ∫ 0.616
dV
V
0.308 1
0.308
= −8.314 × 1146 ∫ 0.616 dV + 8.314 ×1.373 × 10 3 ∫ 0.616 dV
V
0.308
= −8.314 × 1146ln
+ 8.314 × 1.373 × 10 3 (0.308 − 0.616)
0.616
= 6604 − 3516 = 3088J
(b) (10 pts)
∆E = E 2 − E1
5
= R(T2 − T1 )
2
5
= 8.314 × (450 − 27)
2
= 8792J
First law of thermodynamics: ， ∆E = q + w ;
q = ∆E − w
= 8792J − 3088J
= 5704J
26