Die Trigonometrischen Funktionen

Kantonsschule Solothurn
Trigonometrische Funktionen
RYS
Die Trigonometrischen Funktionen
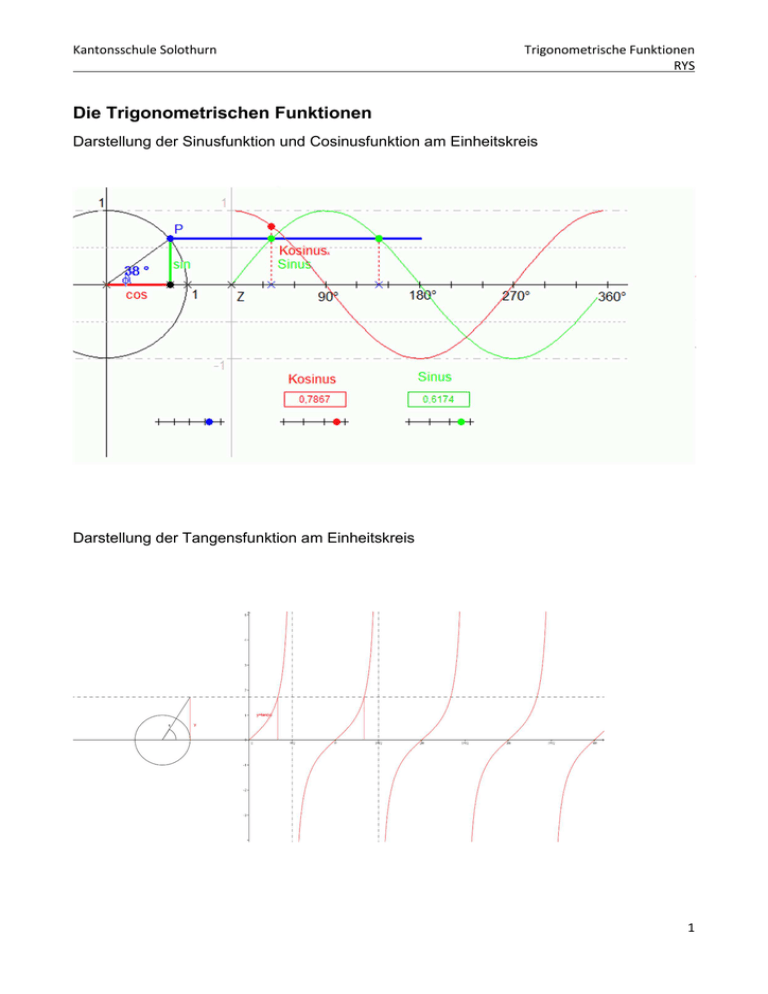
Darstellung der Sinusfunktion und Cosinusfunktion am Einheitskreis
Darstellung der Tangensfunktion am Einheitskreis
1
Eigenschaften der Sinus- und Kosinus- und Tangensfunktion (k ∈ Z)
y = sinx
y = cosx
y = tanx
Definitionsbereich
D=R
D=R
D = R \ { + k∙π }
Wertebereich
W = [-1 , 1]
W = [-1 , 1]
W=R
Periode
2π
2π
π
Symmetrie
ungerade
gerade
ungerade
Nullstellen
k∙π
Relative Maxima
Relative Minima
Polstellen
+ k∙2π
+ k∙2π
-
+ k∙π
k∙π
k∙2π
-
π + k∙2π
-
-
+ k∙π
Kantonsschule Solothurn
Trigonometrische Funktionen
RYS
Einfache Gleichungen und Anzahl Lösungen
Ermittle jeweils die Grösse des Winkels x für das Intervall [0 , 360°]
1. sin(x) = 0.8
2. sin(x) = -0.8
3. sin(x) =
√
4. sin(x) = 0
5. sin(x) = 1
6. sin(x) = -1
Lösungen
1. 0.93 / 2.21
2. 4.07 / 5.36
3. π/3 / 2/3 π
4. 0 / π / 2 π
5. π/2
6. 3/2 π
3
Ermittle jeweils die Grösse des Winkels x für das Intervall [0 , 360°]
1. cos(x) = 0.8
2. cos(x) = -0.8
3. cos(x) =
√
4. cos(x) = 0
5. cos(x) = 1
6. cos(x) = -1
Lösungen
1. 0.65 / 5.64
2. 2.5 / 3.79
3. π/6 / 11/6 π
4. π/2 / 3/2 π
5. 0 / 2 π
6. π
Kantonsschule Solothurn
Trigonometrische Funktionen
RYS WS 14/15
Ermittle jeweils die Grösse des Winkels x im Intervall [0 , 2π]
1. tan(x) = 0.8
2. tan(x) = -0.8
3. tan(x) =
√
4. tan(x) = 0
5. tan(x) = 1
6. tan(x) = -1
Lösungen
1. 0.65 / 3.82
2. 2.47 / 5.61
3. 0.71 / 3.86
4. 0 / π / 2π
5. π/4 / 5/4π
6. 3/4π / 7/8π
5
Die allgemeine Sinus- und Cosinusfunktion
y = a∙sin(bx + c) + d
bzw.
y = a∙cos(bx + c) + d
Bedeutung der Parameter :
a : Die Kurve wird in y-Richtung gedehnt oder gestaucht (Amplitude)
b : die Periode wird verändert zu : Periode p = 2π/b
c : Verschiebung der Kurve längs der x-Achse
d : Verschiebung der Kurve längs der y-Achse
1. Stelle grafisch dar im Bereich [0,2π):
a. y = 2sin(x)
b. y = 0.5sin(x)
c. y = -2sin(x)
d. y = sin(2x)
e. y = sin( x)
f. y = cos(x + π)
g. y = cos(2x) + 1
h. y = 2sin(x - π/2)
i. y = 0.5cos(x) – 2
j. y = 2cos(2x) + 1
k. y = -[sin(x + π) + 1]
2. Berechne jeweils die Nullstellen.
3. Bestimme jeweils den Wertebereich.
Lösungen
a 0, π, 2π
b 0, π, 2π
c 0, π, 2π
d 0, π/2, π, 3/2π, 2π
e0
f π/2, 3/2π
g π/2, 3/2π
h π/2, 3/2π
i keine
j π/3, 2/3π, 4/3π, 5/3π
k 3/2π
W = [-2,2]
W = [-0.5,0.5]
W = [-2,2]
W = [-1,1]
W = [-1,1]
W = [-1,1]
W = [0,2]
W = [-2,2]
W = [-2.5,-0.5]
W = [-1,3]
W = [-2,0]
Kantonsschule Solothurn
Trigonometrische Funktionen
RYS WS 14/15
Lösen von Gleichungen im Intervall [0°,360°] bzw. [0,2π]
1. sin(x) = 0.5
2. 2⋅sin(x) = -0.5
3. 0.5⋅sin(x) = 0.5
4. -2⋅sin(x) = 0.5
5. sin(4x) = 0
6. sin(2x) = 0.5
7. cos(x) = -0.3
8. 2⋅cos(x) = 0.3
9. 0.5⋅cos(x) = -0.3
10. -2⋅cos(x) = 0.3
11. cos(3x) = -0.5
12. cos(2x) = 0.5
13. cos(0.5x) = 0.4
14. tan(x) = 0.5
15. tan(x) = -0.5
16. tan(2x) = -4
17. tan(x + 2) = -3
18. 2⋅tan(3x) = 1
Lösungen
1. π/6 / 5/6π
2. 3.39 / 6.03
3. π/2
4. 3.39 / 6.03
5. 0, π /4, π/2, 3/4π, π, 5/4π, 3/2π, 7/4π, 2π
6. π/12
7. 1.88 / 4.41
8. 1.42 / 4.86
9. 2.21 / 4.07
10.
11.
12.
13.
14.
15.
16.
17.
18.
1.72 / 4.56
0.7 / 1.4 / 2.8 / 3.5 / 4.9 / 5.6
π/6, 5/6π, 7/6π, 11/6π
2.31
0.46 / 3.61
2.68 / 5.82
0.91 / 2.48 / 4.05 / 5.62
3.02 / 6.18
0.15 / 1.20/ 2.25 / 3.3 / 4.34 / 5.39
7
Schwierigere Gleichungen
Bekannte Formeln :
•
tan(x) =
•
•
•
sin2(x)
( )
( )
+ cos2(x) = 1
sin(2x) = 2sin(x)cos(x)
cos(2x) = 1 – 2sin2(x) = 2cos2(x) – 1 = cos2(x) – sin2(x)
Bekannte Lösungsverfahren :
•
•
•
Quadratische Gleichungen
Faktorisieren
Substitution
1. sin(x) = - cos(x)
2. 0 = sin(x) – cos(x)
3. 0 = 2⋅sin(x) – cos(x)
4. 0 = sin(2x) + sin(x)
5. 0 = 0.5⋅sin(x) + 3⋅cos(x)
6. 2⋅cos2(x) – 7⋅cos(x) + 3 = 0
7. sin2(x) – 3⋅cos2(x) = 1
8. sin(x) + cos(x) =
( )
9. cos(2x) = 3⋅cos(x) – 2
10. cos(x) + cos(2x) = 0
11. 2(1 – cos(2x)) = 3⋅sin(2x)
12. sin2(x) – 6⋅cos2(x) + sin(x)cos(x) = 0
Lösungen
1. 3/4π / 7/4π
2. π/4 / 5/4π
3. 0.46 / 3.61
4. 0 / 2/3π / π / 5/3π / 2π
5. 1.74 / 4.88
6. π/3/ 5/6π
7.
8.
9.
10.
11.
12.
π/2 / 3/2π
0 / π/4 / π / 5/4π / 2π
0 / 5/6π / 2π
π/3 / π
0 / 0.98 / π / 4.12 / 2π
1.11 / 1.89 / 4.25 / 5.03