Algorithmik II 6. ¨Ubung Aufgabe 10 Binäre Bäume a) Fügen Sie in
Werbung
Algorithmik II
Aufgabe 10
6. Übung
Binäre Bäume
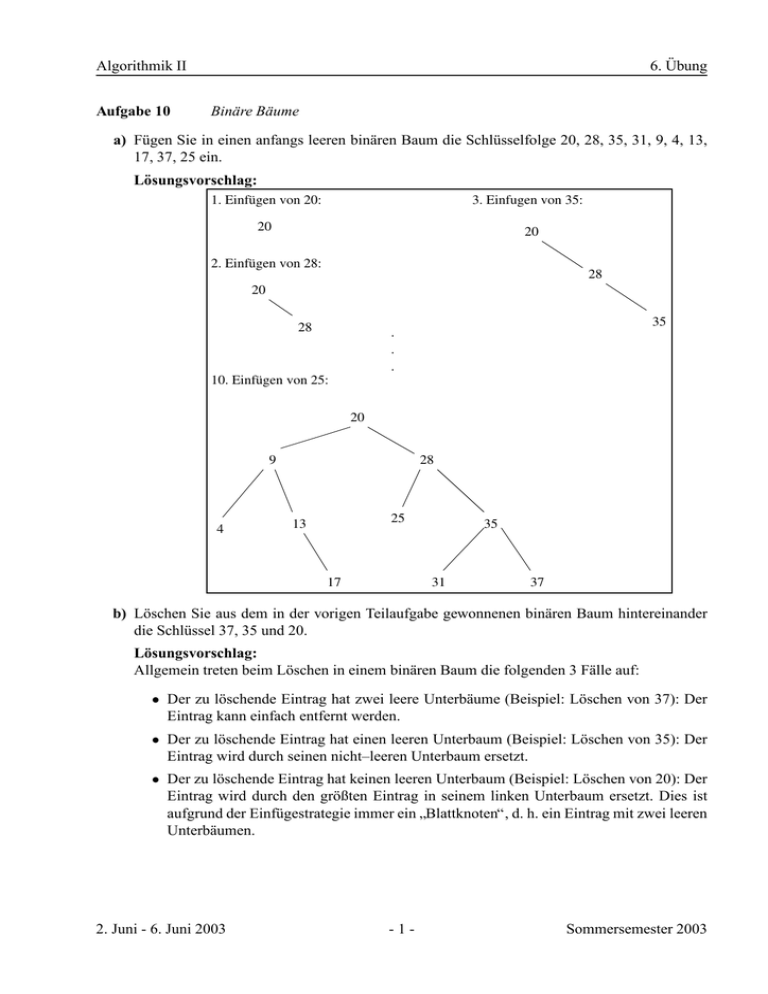
a) Fügen Sie in einen anfangs leeren binären Baum die Schlüsselfolge 20, 28, 35, 31, 9, 4, 13,
17, 37, 25 ein.
Lösungsvorschlag:
1. Einfügen von 20:
3. Einfugen von 35:
20
20
2. Einfügen von 28:
28
20
28
35
.
.
.
10. Einfügen von 25:
20
9
4
28
25
13
17
35
31
37
b) Löschen Sie aus dem in der vorigen Teilaufgabe gewonnenen binären Baum hintereinander
die Schlüssel 37, 35 und 20.
Lösungsvorschlag:
Allgemein treten beim Löschen in einem binären Baum die folgenden 3 Fälle auf:
• Der zu löschende Eintrag hat zwei leere Unterbäume (Beispiel: Löschen von 37): Der
Eintrag kann einfach entfernt werden.
• Der zu löschende Eintrag hat einen leeren Unterbaum (Beispiel: Löschen von 35): Der
Eintrag wird durch seinen nicht–leeren Unterbaum ersetzt.
• Der zu löschende Eintrag hat keinen leeren Unterbaum (Beispiel: Löschen von 20): Der
Eintrag wird durch den größten Eintrag in seinem linken Unterbaum ersetzt. Dies ist
aufgrund der Einfügestrategie immer ein Blattknoten“, d. h. ein Eintrag mit zwei leeren
”
Unterbäumen.
2. Juni - 6. Juni 2003
-1-
Sommersemester 2003
Algorithmik II
6. Übung
1. Löschen von 37:
20
9
28
25
13
4
17
35
31
2. Löschen von 35:
20
9
28
25
13
4
31
17
3. Löschen von 20:
17
9
4
2. Juni - 6. Juni 2003
28
25
13
-2-
31
Sommersemester 2003
Algorithmik II
Aufgabe 11
6. Übung
AVL-Bäume
a) Fügen Sie in einen zu Beginn leeren AVL(1)–Baum die Schlüsselfolge 10, 20, 30, 40, 50, 60,
70, 80 ein.
Lösungsvorschlag:
2. Juni - 6. Juni 2003
-3-
Sommersemester 2003
Algorithmik II
6. Übung
10|2
10|0
20|0
10|1
2
3
R
20|1
10|0
20|0
30|0
30|0
20|1
20|2
4
5
10|0
30|1
10|0
30|2
40|0
40|1
50|0
20|2
20|1
R
6
10|0
10|0
40|0
30|0
40|1
30|0
50|0
50|1
60|0
40|0
40|1
R
7
20|0
10|0
50|1
30|0
20|0
60|0
10|0
50|2
30|0
60|1
70|0
40|0
40|1
R
8
20|0
10|0
60|0
30|0
50|0
20|0
70|0
10|0
60|1
30|0
50|0
70|1
80|0
Das Beispiel zeigt sehr deutlich, daß das Einfügen einer bereits sortierten Folge in einen
AVL–Baum einen gewaltigen Reorganisationsaufwand benötigt. Nachdem die Folge in aufsteigender Reihenfolge sortiert ist, werden nur linke“ Einfachrotationen ausgeführt.
”
2. Juni - 6. Juni 2003
-4-
Sommersemester 2003
Algorithmik II
6. Übung
b) Geben Sie eine Reihenfolge für die Zahlen 10,. . . , 80 an, so daß ihre aufeinanderfolgende
Einfügung in einen zunächst leeren AVL(1)–Baum keine Rotationsoperation benötigt.
Lösungsvorschlag:
Aus dem unter a) gewonnen AVL–Baum kann man eine solche Reihenfolge direkt ablesen,
z. B.
40, 20, 60, 10, 30, 50, 70, 80
Weitere Möglichkeiten sind
• 40, 60, 20, 50, 70, 10, 30, 80
• 40, 60, 20, 50, 10, 70, 30, 80
• 40, 60, 20, 30, 50, 70, 10, 80
• ...
2. Juni - 6. Juni 2003
-5-
Sommersemester 2003
Algorithmik II
6. Übung
c) Fügen Sie in den in Teilaufgabe a) entstandenen AVL-Baum nun den Schlüssel 75 ein.
Lösungsvorschlag:
Hier ist eine Doppelrotation notwendig.
40|2
40|1
20|0
10|0
20|0
60|1
30|0
50|0
60|2
75
10|0
70|1
30|0
50|0
70|2
80|-1
80|0
75|0
40|1
20|0
60|1
R
10|0
30|0
50|0
75|0
70|0
Aufgabe 20
80|0
B-Bäume
a) Fügen Sie die Schlüsselfolge 6, 21, 29, 3, 13, 19, 8, 11, 5, 7, 15 in einen anfangs leeren
B–Baum der Ordnung 2 ein.
Lösungsvorschlag:
2. Juni - 6. Juni 2003
-6-
Sommersemester 2003
Algorithmik II
6. Übung
Einfügen von 6, 21, 29 und 3:
6
6, 21
6, 21, 29
3, 6, 21, 29
Einfügen von 13:
13
3, 6
21, 29
Einfügen von 19, 8 und 11:
13
3, 6, 8, 11
19, 21, 29
Einfügen von 5:
6, 13
3, 5
8, 11
19, 21, 29
Einfügen von 7 und 15:
6, 13
3, 5
7, 8, 11
15, 19, 21, 29
Das Einfügen der ersten vier Schlüssel bereitet keinerlei Schwierigkeiten. Die Wurzel eines
B–Baums der Ordnung 2 kann zwischen einem und vier Elementen enthalten. Man muß somit
beim Eintragen der ersten vier Schlüssel nur auf die richtige Reihenfolge im Wurzelknoten
2. Juni - 6. Juni 2003
-7-
Sommersemester 2003
Algorithmik II
6. Übung
achten.
Das Einfügen der 13 erfordert ein neues Niveau. Nachdem der einzufügende Schlüssel in
der Mitte der bereits vorhandenen Schlüssel liegt, wird 13 zum einzigen Element der neuen
Wurzel. Die bereits vorhandenen Schlüssel werden gleichmäßig - unter Beachtung der Reihenfolge - auf zwei Knoten aufgeteilt.
Das Einfügen der nun folgenden Schlüssel 19, 8 und 11 ist problemlos möglich, da die Knoten des Niveaus 1 noch ausreichend Platz bieten. Zum Eintragen des Schlüssels 5 ist die
Einführung eines neuen Knotens notwendig. Da der Schlüssel 5 in die linke Hälfte des vollen
Knotens gehört, wird der links von der Mitte stehende Schlüssel (6) nach oben gezogen“.
”
Das Einfügen der Schlüssel 7 und 15 ist ohne Schwierigkeiten möglich.
b) Löschen Sie aus dem in der vorigen Teilaufgabe gewonnen B–Baum nacheinander die
Schlüssel 13 und 6.
Lösungsvorschlag:
Löschen von 13:
6, 11
3, 5
7, 8
15, 19, 21, 29
Löschen von 6:
1. Phase:
5, 11
3
7, 8
15, 19, 21, 29
2. Phase:
11
3, 5, 7, 8
15, 19, 21, 29
Das Löschen eines Schlüssels, der nicht Element eines Blattknotens ist, geschieht wie folgt:
2. Juni - 6. Juni 2003
-8-
Sommersemester 2003
Algorithmik II
6. Übung
Zuerst wird der Schlüssel durch den größten Schlüssel seines linken Teilbaums ersetzt. Für
den Fall, daß der resultierende Baum noch ein B–Baum ist, d. h. der Blattknoten aus dem
gelöscht wurde, noch genügend Elemente hat, ist der Löschvorgang nach diesem Schritt beendet (Beispiel: Löschen von 13). Ansonsten ist nach einem Nachbarknoten zu suchen, der
mehr Elemente als notwendig hat, oder es sind zwei Nachbarknoten zu verschmelzen. Beim
Löschvorgang für den Schlüssel 6 hat der Nachbarknoten des defizitären Knotens gerade
ausreichend viele Elemente. Somit ist eine Verschmelzung notwendig. Eine Verschmelzung
hat natürlich auch immer zur Folge, daß das Zwischenelement des Elternknotens der zu verschmelzenden Knoten aufzulösen ist (5).
Rechnerübung 10
Binäre Bäume
Sie haben in der Vorlesung Binäre Bäume kennengelernt. Schreiben Sie nun in Java eine Methode
height, die die Höhe eines Baumes berechnet.
Die Programm-Quellen für eine mögliche Implementierung von binären Bäumen in Java finden
Sie auf der Homepage zu den Übungen im WWW.
Lösungsvorschlag:
class TreeNode {
...
public int height() {
int leftHeight = 0; int rightHeight = 0;
if(left != null)
leftHeight = left.height();
if(right != null)
rightHeight = right.height();
return (1 + Math.max(leftHeight, rightHeight));
}
}
public class Tree {
...
public int height() {
if(rootNode != null)
return rootNode.height();
else
return 0;
}
}
2. Juni - 6. Juni 2003
-9-
Sommersemester 2003











