4. Übungsblatt zur Vorlesung Physik für Pharmazeuten 13

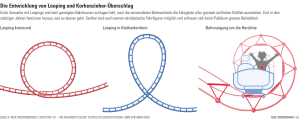
4. Übungsblatt zur Vorlesung Physik für Pharmazeuten
Vorlesungsdatum:
Besprechung:
13
Vorlesung am 14. November 2016
Übungen ab 21. November 2016
Reifenwechsel
Autoreifen werden über spezielle Muttern und Schrauben am Fahrwerk eines Autos befestigt. Beim Wechsel der
Reifen ist insbesondere wichtig, die Muttern mit einem deniertem Drehmoment anzuziehen (festzuschrauben).
Werden sie zu schwach angezogen, drohen die Reifen während der Fahrt abzufallen. Zu festes Anziehen kann die
Schrauben reissen lassen. Aus diesem Grund geben Hersteller ein optimales Drehmoment zum Befestigen der Muttern an. Dieses beträgt im Allgemeinen 120 Nm. Welches Gewicht müsste man am Griende eines 50 cm langen
Drehmomentschlüssels aufbringen, um das nötige Drehmoment zu erreichen?
14
Motorradfahrer
zur
Motorradfahrer müssen sich beim Durchfahren von Kurven in die Kurve legen (einen Winkel kleiner 90
Fahrbahn einnehmen). Der Grund hierfür ist die Fliehkraft (Zentripetalkraft), welche in Kurven auf den Masseschwerpunkt des Systems betehend aus Motorrad+Fahrer wirkt. Die Fliehkraft erzeugt über den Hebel zwischen
dem Kontaktpunkt der Reifen mit der Fahrbahn (1) und dem Masseschwerpunkt (2) ein Drehmoment, welches
zum Umkippen des Motorrads führt. Das Hineinlegen erzeugt über die Schwerkraft ein entgegengesetzt gerichtetes
Drehmoment, was dies verhindert.
Welchen Winkel zwischen Fahrbahn und Hebel müsste das Motorrad einnehmen, damit es bei einer Geschwindig-
v = 80 km=h und einem Kurvenradius von 40 m (Standardradius einer 400 m Leichtathletikbahn) nicht
umkippt? Die Masse des Fahrers beträgt mF = 75 kg , die des Motorrads mM = 200 kg . Der Hebel ist L = 90 cm,
m
die Erdbeschleunigung beträgt g = 9:81 2 .
s
keit von
15
Looping
Ein Skifahrer der Masse m = 70 kg steht auf einer Rampe der Höhe h. Am Fuÿ der Rampe bendet sich ein Looping
mit dem Radius r = 15 m. Beim Einstieg in die Rampe hat er die Geschwindigkeit
a)
v1 = 0 m=s.
Der Skifahrer wird für Testzwecke zusätzlich von einem Schienensystem im Looping gehalten, sodass er bei zu
geringer Geschwindigkeit nicht herunter fallen kann. Wie hoch muss die Rampe mindestens sein, damit er in diesem
Fall durch das Looping kommt?
b)
Der Normalbetrieb des Loopings ndet ohne sicherndes Schienensystem statt. Wie hoch müsste in diesem Fall
die Rampe sein, damit der Skifahrer ohne Herunterfallen durch das Looping gelangt?
c)
Wie groÿ ist die Geschwindigkeit des Skifahrers im höchsten Punkt des Loopings?
16
Hamster im Laufrad
Ein Hamster der Masse
m = 85 g
treibe ein Laufrad der Masse
M = 250 g
und dem Radius
r = 11 cm an.
r vom
Das Laufrad kann als dünner Zylinder behandelt werden, der Hamster als punktförmige Masse im Abstand
Zentrum des Laufrades. Der Hamster bewege sich mit einer Geschwindigkeit von
v = 35 cm
s .
! und den Drehimpuls L des Laufrades ohne Hamster!
a)
Berechnen Sie die Winkelgeschwindigkeit
b)
Durch einen unglücklichen Zufall verklemme sich der Hamster mit den Pfoten im Laufrad und dreht sich dann
mit diesem mit. Berechnen Sie mit Hilfe des Drehimpulserhaltungssatzes die Winkelgeschwindigkeit
sich das Rad mit dem nun eingeklemmten Hamster dreht!
!0 ,
mit der