Relativität elektrischer und magnetischer Felder Lie.

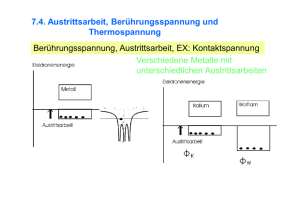
Relativität elektrischer und magnetischer Felder
Lie.
Elektrische und magnetische Felder haben wir bis jetzt als grundsätzlich
verschiedene Phänomene erfahren. Wir wollen nun zeigen, dass dieser Unterschied
teilweise vom Bezugssystem abhängt. Wir wollen auch die Zusammenhänge
zwischen den Feldern in verschiedenen Bezugssystemen untersuchen.
1. Ein B-Feld kann durch Wechsel des Bezugssystems als E-Feld erscheinen.
a) Für einen Beobachter bewege sich ein Teilchen der Ladung q mit Geschwindigkeit
r
r
r
r r
u durch ein reines B - Feld. Auf das Teilchen wirkt die Lorentzkraft F = qu ¥ B .
r
b) Ein zweiter Beobachter, der mit u neben dem Teilchen fliegt, stellt eine Beschleu† Anfangsgeschwindigkeit
nigung des Teilchens fest. Da für ihn das Teilchen keine
r
r
†
hat, folgert er, dass eine elektrische Kraft wirken muss: F =†qE .
c) Da es sich um dieselbe†Kraft handelt, muss eine Messung in beiden
r
r r
Bezugssystemen denselben Wert ergeben: qE = qu ¥ B . Aus dieser Gleichung kann
†
man q entfernen. Man erhält für den Zusammenhang
zwischen den Feldern in zwei
r
Bezugssystemen, die sich mit Geschwindigkeit u gegeneinander bewegen, die
r r r
†
Beziehung E = u ¥ B .
†
†
† Bezugssystems als B-Feld erscheinen.
2. Ein E-Feld kann durch Wechsel des
Wie†man schon durch Kontrolle der Einheiten feststellen kann, lautet die Beziehung
r r r
nicht einfach B = u ¥ E . Hier sind detailliertere Überlegungen notwendig:
Ein unendlich langer, dünner Draht sei gleichmässig mit Ladung belegt. Die
†
Ladung ruhe auf dem Draht. Die Ladungsdichte auf dem Draht sei l = dQ /dl .
Der Beobachter B1 sitze auf dem Draht, der Beobachter B2 bewege sich im Abstand
r
r mit Geschwindigkeit u parallel zum Draht (Figur 1 und 2).
†
†
†
Figur 1: Beobachter B1 folgert, dass am Ort von B2 ein elektrisches Feld
vorhanden sein muss. Die Stärke dieses Feldes ist, wie wir an früherer
Stelle berechnet haben,
1 l
E=
2pe0 r
Figur 2: Für den zweiten Beobachter bewegt sich die Ladung auf dem
Draht, d.h. er beobachtet einen Strom der Stärke
dQ dQ dl
I=
=
⋅ = lu .
dt
dl dt
mI
Mit diesem Strom ist ein B-Feld verbunden: B = 0
2p r
†
†
Wir wollen nun eine Beziehung zwischen den Erkenntnissen aus Fig. 1 und 2 finden:
m I m lu
1 l
e l
1 l
B= 0 = 0
= m0u
= m0u 0
= e0m0u
= e0m0uE
2p r 2p r
2p r
2pe0 r
2pe0 r
Wir haben nun eine Beziehung zwischen den Stärken der Felder, betrachten wir nun
r
die Richtungen. Für Beobachter B1 zeigt E in radialer Richtung vom Draht weg. Für
r
† Beobachter B2 steht B senkrecht zur Drahtrichtung, in Figur 2 am Ort von B2 aus der
r
r r
Zeichenebene heraus. Man kann sich überlegen, dass B parallel zu -u ¥ E ist. Wir
r
r r
†
erhalten somit für den Zusammenhang
der zwei Felder:
B = -e0m0u ¥ E
† e m lässt sich noch eindrücklicher schreiben:
Die Konstante
0 0
-2
2
Ê
Vs
As †
s†
mˆ
1
e0m0 = 4 p ⋅10-7
⋅ 8.854 ⋅10-12
= 1.113⋅10-17 2 = Á3.00 ⋅108
˜ = 2
Am
Vm
m Ë
s¯
c
†
r
r
r
1
†also: B = - u ¥ E
c2
† Hinweis: Die Formeln gelten nur für Geschwindigkeiten, die klein gegen die
Lichtgeschwindigkeit sind, und sie beschreiben lediglich einen Teilaspekt. Die
†
vollständigen
Transformationsgleichungen findet man in der speziellen
Relativitätstheorie Albert Einsteins (1905).
3. Folgerungen.
r r r
Die Beziehung E = u ¥ B besagt, dass aus einem Magnetfeld ein elektrisches Feld
herauswachsen kann. Dies führt zum Induktionsgesetz von Faraday.
r
r r
†
Die Beziehung
B = -e0m0u ¥ E besagt, dass aus einem elektrischen Feld ein
magnetisches Feld herauswachsen kann. Dies führt zum Gesetz von Maxwell.
† vom Bezugssystem ab, wie gross die Anteile elektrischer und magnetischer
Es hängt
Feldstärken sind. Eine umfassende Theorie elektrischer und magnetischer
Phänomene hat dies zu berücksichtigen. Die Elektrodynamik vom engl. Physiker
James Clerk Maxwell (1831-1879) tut das. Seine Theorie (1864) ist heute noch die
Grundlage fast der gesamten Elektrotechnik. Die spezielle Relativitätstheorie Albert
Einsteins ist aus ihr herausgewachsen. Die Maxwellschen Gleichungen beschreiben
aber keine Quantenphänomene (Supraleitung, Elementarladung, ...).
Die Formel c = 1/ e0m0 stammt von Weber (1846), der Wert wurde von Weber und
Kohlrausch 1856 gemessen. Die Formel legte nahe, dass Licht ein
elektromagnetisches Phänomen ist. Damit wurde die Optik ein Teil der
†
Elektrodynamik.
Licht ist eine elektromagnetische Welle. Ein sich zeitlich änderndes
elektrisches Feld erzeugt ein zeitlich änderndes Magnetfeld, dieses wieder ein
elektrisches Feld, dieses wieder ein magnetisches und so fort. Auf diese Weise
können sich elektromagnetische Felder im Raum ausbreiten.