(2,3)-Baum ein

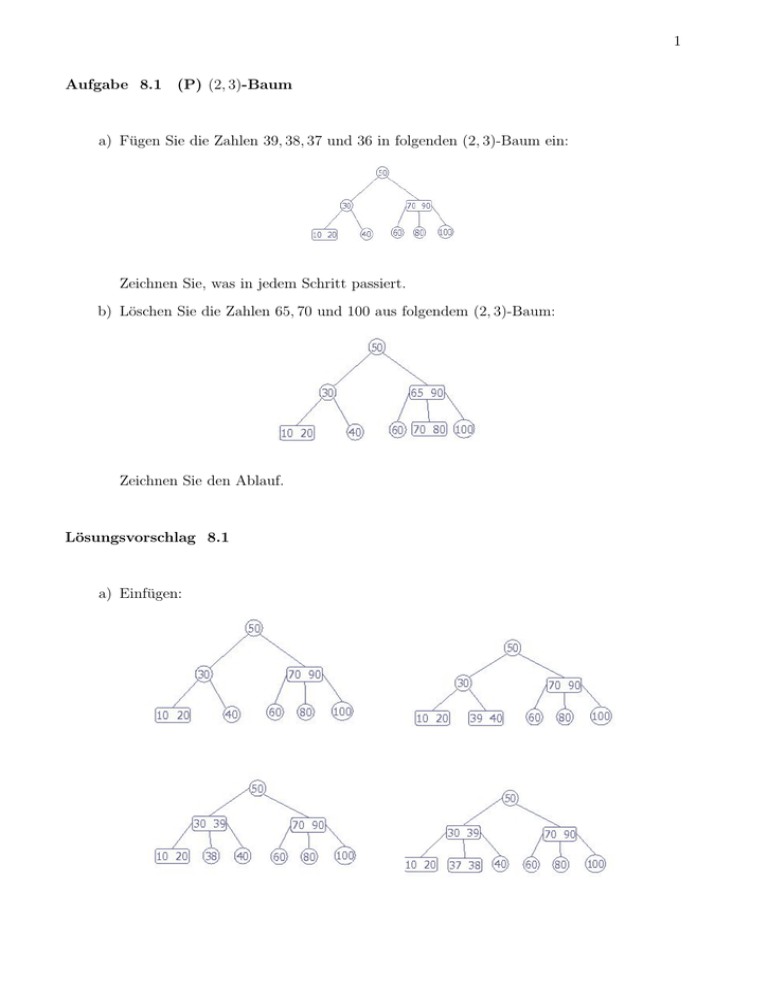
1
Aufgabe 8.1 (P) (2, 3)-Baum
a) Fügen Sie die Zahlen 39, 38, 37 und 36 in folgenden (2, 3)-Baum ein:
Zeichnen Sie, was in jedem Schritt passiert.
b) Löschen Sie die Zahlen 65, 70 und 100 aus folgendem (2, 3)-Baum:
Zeichnen Sie den Ablauf.
Lösungsvorschlag 8.1
a) Einfügen:
2
b) Löschen:
Aufgabe 8.2 (P) Rot-Schwarz-Bäume
Ein Rot-Schwarz-Baum ist ein binärer Suchbaum, dessen Knoten entweder rot oder schwarz
gefärbt sind und die folgenden 5 Regeln erfüllt:
• Der Schlüssel eines Vaterknotens ist grösser als der Schlüssel seines linken und kleiner
als der Schlüssel seines rechten Kindknotens.
• Ein Knoten ist entweder schwarz oder rot
• Die Wurzel ist schwarz
• Ein Pfad, von der Wurzel zu einem Endknoten, hat gleich viele schwarze Knoten.
• Ein roter Knoten, hat nur schwarze Kindknoten (d.h. es folgen niemals zwei rote
Knoten aufeinander).
Mehr Informationen finden Sie, zum Beispiel hier:
3
http://www.math.bas.bg/ nkirov/2009/NETB201/slides/ch09/ch09b.html
http://www.computerperception.ch/ctr/archive/project1/RBTree1/description/rbtree.html
http://de.wikipedia.org/wiki/Rot-Schwarz-Baum
a) Finden Sie eine Darstellung von Rot-Schwarz-Bäumen durch geeignete (a,b)-Bäume.
b) Überlegen Sie sich einen Algorithmus zum Einfügen in Rot-Schwarz-Bäumen und testen sie ihn Anhand des Beispiels aus der Vorlesung zum Einfügen in (a,b)-Bäumen
(p42ff).
c) Diskutieren Sie, welche Probleme beim Einfügen in Rot-Schwarz-Bäumen auftreten
und vergleichen Sie es mit dem Löschen in (a,b)-Bäumen.
Lösungsvorschlag 8.2
a) Rot-Schwarz-Bäume sind eine Darstellung von (2, 4)-Bäumen, man wandelt die Knoten
eines (2, 4)-Baumes nach folgendem Schema um (Kreise repräsentieren Teilbäume):
=⇒
a
Grad 2 Knoten
1
a
2
1
2
=⇒
a, b
b
a
Grad 3 Knoten
1
2
3
1
3
2
=⇒
a, b, c
b
a
Grad 4 Knoten
1
2
3
4
1
c
2
3
4
b) Zunächst fügt man wie bei einem normalen binären Suchbaum ein und färbt den neuen
Knoten (k) rot. Falls der Vaterknoten schwarz ist, bleiben alle Eigenschaften erfüllt
und es ist nichts weiter zu tun. Ist der Vaterknoten rot, müssen wir eine Korrektur
durchführen und unterscheiden hierzu zwei Fälle:
Schwarzer Nachbar: Dies entspricht einer ’falschen’ Anordnung der Teile eines 4-Knotens
und wird durch folgende Umsortierung behoben:
g
=⇒
k
n
1
g
v
1’
2
n
4
k
3
1
v
2
1’
3
4
4
Roter Nachbar: Dies entspricht dem ’split’-Fall im (2, 4)-Baum und hat hier ein Umfärbung der Knoten zufolge und ebenfalls einen rekursiven Aufruf dieser Prozedur,
sollte sich der Farbkonflikt für den Großvaterknoten (g) wiederholen. Wird bei
diesem Vorgehen die Wurzel des gesamt Baumes erreicht, so wird sie nicht rot
gefärbt und das Verfahren terminiert, was dem Entstehen eines neuen Wurzelknotens entspricht.
g
g
=⇒
n
1
v
2
4
k
3
n
1
v
2
3
3’
4
k
3’
Den (2, 4)-Baum aus dem Vorlesungsbeispiel kann man wie folgt darstellen:
14
5
28
3
10
19
42
Führt man auf diesem Baum Insert(8); aus erhält man:
14
5
28
3
10
19
42
8
Anschließend Insert(32); liefert:
14
5
28
3
10
8
19
42
32
Der hier entstehende Rot-Schwarz-Baum enspricht nicht der Umsetzung des Baums des
Beispiels, da nicht das Element rechts der Mitte nach oben geschoben wird, sondern das
Ältere. Dies wäre auch für den (2, 4)-Algorithmus eine Möglichkeit, denn welches der
beiden mittleren Elemente benutzt wird, ist für die Struktur und Effizienz des Baumes
nicht wichtig. Man benötigt lediglich ein deterministisches Verfahren zur Bestimmng
des Elements. Welches Verfahren man schließlich wählt liegt im eigenen Ermessen.
Der Rot-Schwarz-Baum zur Vorlesung wäre:
5
14
8
32
5
10
28
3
42
19
c) Bereits beim Löschen im (2, 4)-Baum werden mehrere Fälle unterschieden. Betrachtet man nun die direkte Übertragung der (2, 4)-Bäume auf Rot-Schwarz-Bäume und
versucht, Remove entsprechend zu übersetzen, muss man bei Rot-Schwarz-Bäumen
bei diesen Fällen zusätzlich weitere Fälle unterscheiden. Betrachten wir zum Beispiel
den Fall, dass im (2, 4)-Baum zwei Knoten vereinigt werden müssen; konkret folgender
Baum (links im Bild). Wird in diesem Baum die 1 gelöscht, entsteht ein Baum mit
Wurzel 4, linkem Blatt 2, 3 und rechtem Blatt 5 (siehe rechter Baum).
=⇒
2, 4
4
2,3
1
3
5
5
Der entsprechende Rot-Schwarz-Baum kann zwei Varianten haben (durch Einfügen
und Löschen kann die zweite Variante entstehen).
4
2
2
5
1
4
1
3
3
5
Würde man nun das Löschen aus dem (2, 4)-Baum übertragen, muss man diese beiden
Fälle unterscheiden. Entsprechend gibt es auch für die anderen Fälle des Löschens in
(2, 4)-Bäumen wieder Fallunterscheidungen auf den Rot-Schwarz-Bäumen.
Eine ausführliche Diskussion aller Fälle ist hier nicht verlangt. Für die konkrete Umsetzung des Löschens bei Rot-Schwarz-Bäumen finden Sie in der Literatur ausführliche
Erklärungen, z.B. in dem Buch Introductions to Algorithms“ von T.H. Cormen et al.
”
Aufgabe 8.3 [5 Punkte] (H) (a, b)−Baum
a) Fügen Sie in den folgenden (3, 6)-Baum die Elemente 2, 4 und 12 ein. Zeichnen Sie,
was in jedem Schritt passiert.
6
b) Löschen Sie aus dem resultierenden Baum die Elemente 2, 17, 3 und 21. Zeichnen Sie,
was in jedem Schritt passiert.
Lösungsvorschlag 8.3
a) insert 2:
insert 4:
Das linke Blatt hat zuviele Schlüssel, es wird aufgeteilt.
insert 12:
7
Das Blatt hat zuviele Schlüssel, es wird aufgeteilt.
Der innere Knoten hat zuviele Schlüssel, er wird aufgeteilt.
b) remove 2:
remove 17:
8
Das Blatt hat zuwenig Schlüssel, es klaut einen Schlüssel beim linken Nachbarn. Um
die Suchbaumeigenschaft zu erhalten, werden die Schlüssel 13 und 15 rotiert.
remove 3:
Das Blatt hat zuwenig Schlüssel, der einzige Nachbar hat genau a − 1 = 2 Schlüssel,
kann also keinen mehr abgeben. Die beiden Knoten werden gemergt. Da der Vater
dann ein Kind weniger hat, wandert ein Schlüssel (4) runter.
9
remove 21: Da der Schlüssel im inneren Knoten steht, wird er durch den größten
Schlüssel (19), der kleiner ist als er selbst, ersetzt.
Das Blatt, in dem der Schlüssel 19 stand, hat zuwenig Schlüssel, der einzige Nachbar
hat genau a − 1 = 2 Schlüssel, kann also keinen mehr abgeben. Die beiden Knoten
werden gemergt. Da der Vater dann ein Kind weniger hat, wandert ein Schlüssel (13)
runter.
Der Vater hat nun auch zuwenig Schlüssel.Es muss wieder gemergt werden. Da der
Vater dann ein Kind weniger hat, wandert ein Schlüssel (19) runter.
Der resultierende Baum hat eine Wurzel mit nur 2 Kindern. Dies ist in einem (3, 6)Baum nur der Wurzel erlaubt. Für andere innere Knoten wäre die Grad-Invariante
verletzt.
10
Aufgabe 8.4 [5 Punkte] (H) (2,3)-Baum
Beweisen Sie folgende Aussage:
Für einen (2, 3)-Baum gibt es eine Folge von n insert bzw. remove-Operationen, so dass
die Anzahl der nötigen Aufspaltungen und Vereinigungen in Ω(n log n) ist.
Lösungsvorschlag 8.4
Zunächst sorgen wir dafür, dass der (anfangs leere) (2,3)-Baum eine gewisse Anzahl von
Blättern enthält. Wir berechnen dazu die größte Zweierpotenz, die kleiner oder gleich n/2
ist. Dazu sei bemerkt, dass diese Größe n0 = 2blog2 (n/2)c höchstens um den Faktor 1/4 kleiner
als n ist, also Ω(n). Wir fügen also erstmal die Schlüssel von 1 bis n0 in den (2, 3)-Baum ein.
Die restlichen n − n0 Operationen verwenden wir, um abwechselnd immer wieder denselben
Schlüssel mit remove zu entfernen und mit insert wieder einzufügen. Die Anzahl dieser
Operationen ist natürlich auch mindestens halb so groß wie n, also natürlich auch in Ω(n).
Bei jeder remove-Operation wird ein Blatt entfernt, so dass der entsprechende Vater-Knoten
nur noch ein Kind hat. Dieser Knoten muss also mit einem anderen Knoten vereinigt werden.
Der gemeinsame Vater-Knoten hatte vorher jedoch auch nur diese zwei Kinder und muss
nun ebenfalls mit seinem einzigen Bruder verschmolzen werden usw. Dieser Prozess endet
erst an der Wurzel. Umgekehrt wird bei jeder darauffolgenden insert-Operation ein Knoten
mit drei Kindern in zwei Knoten mit je zwei Kindern aufgespalten, was sich auch wieder
bis zur Wurzel fortsetzt. Da die Höhe des Baums mit n0 ∈ Ω(n) Blättern gleich blog2 (n0 )c ∈
Ω(log2 n0 ) ist, beträgt der Gesamtaufwand Ω(n log2 n).
⇐⇒