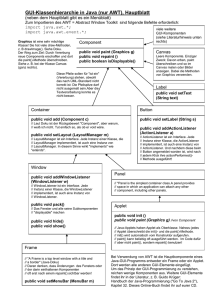
Vortragsfolien (

Modellierung und Simulation
optischer Strahlführungen
Diplomarbeit
Timon Bätz
Übersicht
●
Ziele
●
Physikalische Hintergründe
●
Architektur und Implementierung
●
Ergebnisse
●
Ausblick
●
Demo
2
Ziele
●
Entwicklung eines virtuellen optischen Baukastens für Hochleistungslaser:
- Lineares Aneinanderreihen optischer
Elemente (Linsen, Kristalle …)
- Gruppierung optischer Elemente zu
komplexeren Elementen
●
Simulation linearer Aufbauten mittels:
- Gaußstrahl-Optik
- Fourier-Optik
●
Parallelisierung der mathematischen
Berechnungen für
Echtzeitsimulationen
3
Physik: Wellenoptik
●
Licht wird durch eine skalare
Wellenfunktion beschrieben, welche die
sogenannte Wellengleichung erfüllen
muss:
Laplace-Operator:
4
Physik: Wellenoptik
●
Licht wird durch eine skalare
Wellenfunktion beschrieben, welche die
sogenannte Wellengleichung erfüllen
muss:
Laplace-Operator:
Kreisfrequenz:
●
Wellenfunktion für monochromatische
Wellen:
5
Physik: Wellenoptik
●
Licht wird durch eine skalare
Wellenfunktion beschrieben, welche die
sogenannte Wellengleichung erfüllen
muss:
Laplace-Operator:
Kreisfrequenz:
●
●
Wellenfunktion für monochromatische
Wellen:
Eulersche Relation:
Komplexe Schreibweise:
6
Physik: Wellenoptik
●
Licht wird durch eine skalare
Wellenfunktion beschrieben, welche die
sogenannte Wellengleichung erfüllen
muss:
Laplace-Operator:
Kreisfrequenz:
●
●
Wellenfunktion für monochromatische
Wellen:
Komplexe Schreibweise:
Eulersche Relation:
Komplexe Amplitude:
Amplitude:
●
Trennung der Variablen:
Phase:
Intensität:
7
Physik: Gaußstrahl-Optik
Helmholtz-Gleichung:
(aus der Wellengleichung nach Trennung der Variablen)
Lösungen:
Gaußstrahl
: Radius bei dem die Amplitude auf
Kugelwelle
fällt
●
ABCD-Gesetz:
•
: Radius im Fokus
: Elektrische Feldstärke (z = 0)
: Gouy-Phase
: Wellenzahl
Ebene Welle
•
Jedes optische Element wird
durch eine 2x2 Matrix
beschrieben:
Der Strahlparameter q
wird durch das
ABCD-Gesetz
berechnet:
: Strahlparameter
8
Physik: Gaußstrahl-Optik
Beispiel:
Propagation:
Dünne Linse:
9
Physik: Gaußstrahl-Optik
Grenzen:
●
●
●
Intensität des Strahls wird als Gaußverteilt angenommen
Abstände zwischen den optischen Elementen >> w(z)
→ paraxiale Näherung
Simuliert ausschließlich achsensymmetrische optische Elemente
Fourieroptik
10
Physik: Fourieroptik
Prinzip:
●
●
Eine beliebige Welle kann als Überlagerung mehrerer ebener Wellen beschrieben werden.
Ist die Transformation des optischen System auf eine ebene Welle bekannt, kann durch
das Superpositionsprinzip die Transformation des Systems auf eine beliebige Welle
berechnet werden.
●
Projektion der Eingangswelle auf die z = 0-Ebene:
●
Fourieranalyse:
●
Transformation durch das optische System:
11
Physik: Fourieroptik
Propagation im freien Raum:
●
Betrachtet man eine ebene Welle und Propagation im freien Raum, so gilt:
●
Übertragungsfunktion:
●
Verallgemeinerung auf komplexere Eingangswellen:
●
Berechnungsvorschrift:
Matrix E = getInpunt();
E = fft(E);
E *= H;
E = ifft(E);
12
Physik: Fourieroptik
Fresnelsche Näherung (Nahfeld):
b
Gültigkeit:
Frauenhofer Näherung (Fernfeld):
Gültigkeit:
Quelle: SALEH, B.E.A. ; TEICH, M.C.: Fundamentals of photonics.
13
Physik: Fourieroptik
Optische Elemente mit Ausdehnung d ≈ 0:
Optische Komponenten mit d ≈ 0 können durch eine Transmissionsfunktion / Transmissionsmatrix
beschrieben werden, die in jedem Punkt dem Proportionalitätsfaktor zwischen der Eingangsfunktion
f(x,y) und der Ausgangsfunktion g(x,y) entspricht, so dass:
g(x,y) = t(x,y)f(x,y)
●
Blende:
●
Linse:
14
Architektur
Simulationspipeline:
●
●
Beide Modelle besitzen die Eigenschaft, dass die Transformationen der optischen
Komponenten auf den Laserstrahl unabhängig vom gewählten Laseraufbau sind.
Die Transformationsvorschriften sind einzig und allein von den Parametern der
Komponente abhängig.
Optischen Elemente können modular implementiert und in beliebiger Reihenfolge
aneinandergereiht werden (nach dem Pipeline-Prinzip):
15
Architektur
Simulationspipeline:
●
●
Beide Modelle besitzen die Eigenschaft, dass die Transformationen der optischen
Komponenten auf den Laserstrahl unabhängig vom gewählten Laseraufbau sind.
Die Transformationsvorschriften sind einzig und allein von den Parametern der
Komponente abhängig.
Optischen Elemente können modular implementiert und in beliebiger Reihenfolge
aneinandergereiht werden (nach dem Pipeline-Prinzip):
Caching:
16
Architektur
17
Basic Linear Algebra Subprograms (BLAS)
●
●
●
●
Bezeichnet eine Softwareschnittstelle, die elementare Operationen der linearen
Algebra wie Vektor- und Matrixmultiplikationen implementiert.
Es gibt eine Vielzahl von Implementierungen in verschiedenen Sprachen und für
verschiedene Plattformen optimiert (nicht alle halten sich 100% an das Interface).
Unterstützte Datentypen: float (32 Bit), double (64 Bit), complex (2 x 32 Bit),
doublecomplex (2 x 64 Bit).
Funktionen werden in 3 Stufen unterteilt:
Level 1
Level 2
Level 3
float cblas_sdot(...);
double cblas_ddot(...);
void
void
void
void
cblas_sgemv(...);
cblas_dgemv(...);
cblas_cgemv(...);
cblas_zgemv(...);
void
void
void
void
cblas_sgemm(...);
cblas_dgemm(...);
cblas_cgemm(...);
cblas_zgemm(...);
void
void
void
void
cblas_sgbmv(...);
cblas_dgbmv(...);
cblas_cgbmv(...);
cblas_zgbmv(...);
void
void
void
void
cblas_sgbmm(...);
cblas_dgbmm(...);
cblas_cgbmm(...);
cblas_zgbmm(...);
void
void
void
void
cblas_ssymv(...);
cblas_dsymv(...);
cblas_csymv(...);
cblas_zsymv(...);
void
void
void
void
cblas_ssymm(...);
cblas_dsymm(...);
cblas_csymm(...);
cblas_zsymm(...);
Vektor-Vektor-Operationen
void cblas_sswap(...);
void cblas_scopy(...);
void cblas_saxpy(...);
void cblas_dswap(...);
void cblas_dcopy(...);
void cblas_daxpy(...);
void cblas_cswap(...);
void cblas_ccopy(...);
void cblas_caxpy(...);
Matrix-Vektor-Operationen
Matrix-Matrix-Operationen
18
Architektur: Plugins
●
●
Es wurden 6 Plugins implementiert, welche unterschiedliche Bibliotheken benutzten um
Matrizenoperationen und Fouriertransformationen auszuführen
Jedes Plugin liefert eine zu den verwendeten Bibliotheken kompatible Matrix- und VektorImplementierung
Name
Matrizenoperationen
FFT
Gerät
Genauigkeit
HipnosCBlasMathPlugin
Cblas (netlib, ATLAS,
OpenBlas)
FFTW
CPU
double
HipnosACMLMathPlugin
ACML-BLAS
ACML-FFT
CPU
double
HipnosGSLMathPlugin
GSL-BLAS
GSL-FFT
CPU
double
HipnosCudaMathPlugin
cuBLAS
cuFFT
GPU
double
HipnosCudaMathSinglePrecisionPlugin
cuBLAS
cuFFT
GPU
float
HipnosAPPMLMathPlugin
clAmdBlas
clAmdFft
GPU
double
19
Architektur: GPU-Plugins
Speicherverwaltung:
●
●
●
Moderne GPUs sind
hochperformante MulticoreSysteme, welche auf
datenparalleles Rechnen
spezialisiert sind
Besonders effektiv wenn
das Verhältnis von arithmetischen
Operationen zu
Speicheroperationen sehr hoch
ist
Nachteil: GPU-Plugins
referenzieren Speicher jeweils im
Haupt- und Grafikspeicher
→ Aufwendige Kopieroperationen
20
Ergebnisse
Gaußstrahl-Optik vs Fourieroptik:
21
Ergebnisse
Matrixaddition:
22
Ergebnisse
Matrix-Vektor Multiplikation:
23
Ergebnisse
Matrixmultiplikation:
24
Ergebnisse
Zweidimensionale Fouriertransformation:
25
Ergebnisse
Propagationskomponente (Fresnelsche Näherung):
26
Ausblick
●
Implementierung weiterer optischer Elemente
●
Implementierung weiterer Gauß-Moden
●
Implementierung weiterer optischer Berechnugsmodelle
●
Schnittstelle für Scriptbare Komponenten
●
Modellierung und Simulation von verzweigten Laseraufbauten
●
Octave Integration
●
3D-Visualisierung des gesamten Laseraufbaus
●
Unterstützung für CUDA-Zero-Copy Memory
●
Optimierung der 3D-Visualisierung
27
Demo
28