Hertzsprung-Russell- und Farb-Helligkeits

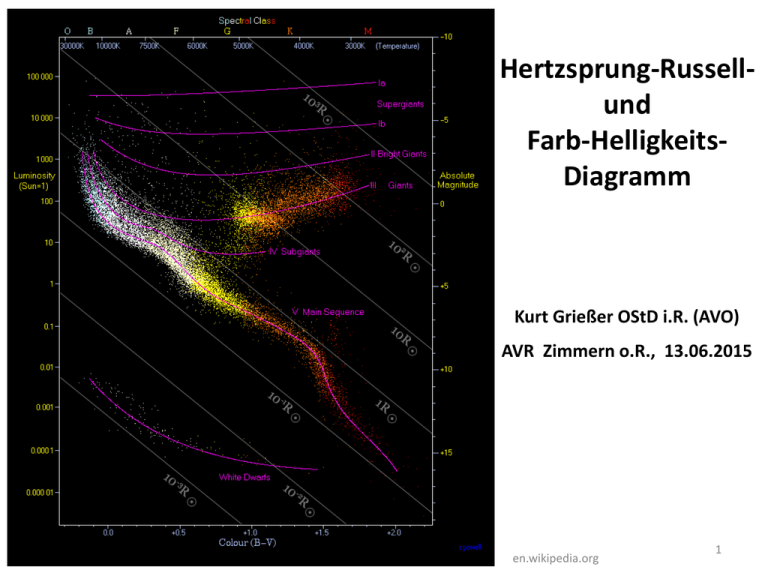
Hertzsprung-Russellund
Farb-HelligkeitsDiagramm
Kurt Grießer OStD i.R. (AVO)
AVR Zimmern o.R., 13.06.2015
en.wikipedia.org
1
Das Hertzsprung – Russel Diagramm
Was verstehen die Astronomen
unter einem Stern?
Man bedenke:
Die Astronomen haben
keinen direkten Zugang
zum Objekt ihrer Forschung.
Ausnahmen:
Allgemeinwissen
direkt:
Mond
indirekt: Mars, Venus
Kometen
Kurt Grießer OStD i.R,
2
Das Hertzsprung – Russel Diagramm
Was verstehen die Astronomen
unter einem Stern?
Wie ist es dennoch möglich aus der
Beobachtung eines Lichtpunktes am Himmel
(elektromagnetische Strahlung)
Aussagen über Eigenschaften dieses Objekts
und dessen Entfernung machen zu können?
Allgemeinwissen
Kurt Grießer OStD i.R,
3
Ziel des Vortrags
Eine graphische Anordnung von
Sternspektren vorzustellen, die gestattet
Sternzustände
(Masse, Radius, Temperatur, Leuchtkraft)
und deren gegenseitige Abhängigkeit
sowie
Sternentwicklungen
(offene Sternhaufen und Kugelsternhaufen)
(Riesenstadium; weiße Zwerge)
übersichtlich darzustellen.
Allgemeinwissen
Kurt Grießer OStD i.R,
4
Ziel des Vortrags
Eine graphische Anordnung von
Sternspektren vorzustellen, die
gestattet
Sternzustände
(Masse, Radius, Temperatur,
Leuchtkraft)
und deren gegenseitige Abhängigkeit
sowie
Sternentwicklungen
(offene Sternhaufen und
Kugelsternhaufen)
(Riesenstadium; weiße Zwerge)
übersichtlich darzustellen.
Allgemeinwissen
Kurt Grießer OStD i.R,
5
Ziel des Vortrags
Eine graphische Anordnung von
Sternspektren vorzustellen, die
gestattet
Sternzustände
(Masse, Radius, Temperatur,
Leuchtkraft)
und deren gegenseitige Abhängigkeit
sowie
Sternentwicklungen
(offene Sternhaufen und
Kugelsternhaufen)
(Riesenstadium; weiße Zwerge)
übersichtlich darzustellen.
Allgemeinwissen
Kurt Grießer OStD i.R,
6
Ziel des Vortrags
Eine graphische Anordnung von
Sternspektren vorzustellen, die
gestattet
Sternzustände
(Masse, Radius, Temperatur,
Leuchtkraft)
und deren gegenseitige Abhängigkeit
sowie
Sternentwicklungen
(offene Sternhaufen und
Kugelsternhaufen)
(Riesenstadium; weiße Zwerge)
übersichtlich darzustellen.
Novapix.net
Kurt Grießer OStD i.R,
7
Beispiele einiger „Zustands-Diagramme“,
die eine
wissenschaftliche Beschreibung
eines Objekts gestatten.
Allgemeinwissen
Kurt Grießer OStD i.R,
8
Periodensystem der Elemente
frustfrei-lernen.de
Kurt Grießer OStD i.R,
9
Beispiel: Personen
A+R 2013 Heft ¾ S.6
HRD im Unterricht
Kurt Grießer OStD i.R,
10
Beispiel: Kraftfahrzeuge
A+R 2013 Heft ¾ S.6
HRD im Unterricht
Kurt Grießer OStD i.R,
11
Welche Eigenschaften haben
die Objekte am Himmel,
die wir nur als Lichtpunkte
beobachten können ?
Allgemeinwissen
Kurt Grießer OStD i.R,
12
Stern ?
Gaskugel, die durch Eigengravitation
zusammengehalten wird.
Quelle der abgestrahlten Energie
sind Kernfusionen,
hauptsächlich im Zentrum der Kugel.
Gravitationsenergie spielt nur
anfänglich (Erwärmung) eine Rolle.
Allgemeinwissen
Kurt Grießer OStD i.R,
13
Sternzustände
Größe (Radius)
Art der Materie
Abs. Helligkeit
Masse
Dichte
Wasserstoff, Helium, „Metalle“
Leuchtkraft
Oberflächentemperatur
Spektrum (HRD und FHD) und dessen Interpretation
Entfernung
scheinbare Hellgkt
eigentlich keine Sterneigenschaft
Beeinträchtigung der Erscheinung
Verweildauer
in einzelnen Entwicklungsphasen
Alter als Entwicklungszustand
Allgemeinwissen
Kurt Grießer OStD i.R,
14
Zustandsgrößen
in Einheiten der Sonne
1
Masse
0,1 < M < 80
Leuchtkraft
0,0001 < L < 1.000.000
Temperatur
3.000 K < T0 < 50.000 K
Radius
mittlere
Dichte
0,0005 < R < 100
14-4 mg/cm³ < ρ < 108 t/cm³
10-7 < ρ < 1014
Paetec Astronomie II S. 159
Kurt Grießer OStD i.R,
15
Sternradien in
Vergleich
kleiner-kalender.de
Kurt Grießer OStD i.R,
17
Fingerzeig des Himmels
kleiner-kalender.de
Kurt Grießer OStD i.R,
20
7 Regenbogenfarben
Allgemeinwissen
Kurt Grießer OStD i.R,
21
6 Regenbogenfarben
Allgemeinwissen
Kurt Grießer OStD i.R,
22
Strahlengang im Regentropfen
Totalreflexion
Allgemeinwissen
Kurt Grießer OStD i.R,
23
Allgemeinwissen
Kurt Grießer OStD i.R,
24
Joseph Fraunhofer
1787 - 1826
leifiphysik.de
Kurt Grießer OStD i.R,
25
Fraunhofer
planet-wissen.de
Kurt Grießer OStD i.R,
26
F - Linien historisch
Internet
Kurt Grießer OStD i.R,
27
Fraunhofer - Linien
Was hat Fraunhofer tatsächlich gesehen ?
wikipedia.org
Kurt Grießer OStD i.R,
28
http://www.astro.uu.se/~ulrike
/Spektroskopie/PPT/Fraunhofe
r_Spektrum.GIF
Kurt Grießer OStD i.R,
29
A
B
A
C
B
http://www.astro.uu.se/~ulrike
/Spektroskopie/PPT/Fraunhofe
r_Spektrum.GIF
D
C
E
D
b
F
E
Kurt Grießer OStD i.R,
G
F
H
G
KH
30
200. Geburtstag
de.wikipedia.org
Kurt Grießer OStD i.R,
31
Pater Angelo Secchi 1818 - 1878
Wikipedia
Kurt Grießer OStD i.R,
32
Pater Angelo Secchi 1818 - 1878
Internet
Kurt Grießer OStD i.R,
33
Mondgebirge Secchi
Wikipedia
Kurt Grießer OStD i.R,
34
Montes Sechchi
en.wikipedia.org
Kurt Grießer OStD i.R,
35
S
F
Wikipedia
Kurt Grießer OStD i.R,
36
Mondkrater Fraunhofer
historisch.astronomie-imchiemgau.de
Kurt Grießer OStD i.R,
37
Mondkrater Fraunhofer
historisch.astronomie-imchiemgau.de
Kurt Grießer OStD i.R,
38
Fraunhofer-Linien des Sonnenspektrums G 2 V
50
40
30
20
10
0
starobserver.org
Kurt Grießer OStD i.R,
39
Arkturus - Fraunhofer-Linien K 2 III
50
40
30
20
10
0
starobserver.org
Kurt Grießer OStD i.R,
40
Procyon - Fraunhofer-Linien F 5 IV
50
40
30
20
10
0
starobserver.org
Kurt Grießer OStD i.R,
41
Diverse Sternspektren
avgoe.de
Kurt Grießer OStD i.R,
42
Sternspektren
Vega (Balmer)
holoenergetic.ch
Kurt Grießer OStD i.R,
43
Spektren
α-Oph: A5 III, β-Cyg: K3 II, α-Her: M5 II
leifiphysik.de
Kurt Grießer OStD i.R,
44
„Vision“ der Astronomen
Diese unterschiedlichen Spektren
haben ihren Grund
in unterschiedlichen Eigenschaften der Sterne.
Fingerabdrücke eines Sterns
Zum Verständnis hierzu muss man zunächst
bei
Mathematikern und Physikern
„Sprachunterricht“ nehmen.
Allgemeinwissen
Kurt Grießer OStD i.R,
45
Wie kommen diese Linien zustande ?
Die vom Stern (im Großen) ausgehende
elektromagnetische Strahlung (einzige Informationsquelle)
entsteht in den Atomen (im Kleinen).
Allgemeinwissen
Kurt Grießer OStD i.R,
46
Wie kommen diese Linien zustande ?
Die wissenschaftliche Untersuchung dieser Strahlung
beschreibt das Verhältnis von Materie und Strahlung.
gibt (begrenzt) Auskunft über die Materie,
aus der die Strahlung stammt
oder
durch die die Strahlung hindurchging.
Allgemeinwissen
Kurt Grießer OStD i.R,
47
3 unterschiedliche Spektren
D.Herrmann S.98
Kurt Grießer OStD i.R,
48
Atombau
Bohr‘sches Modell
h f = E 2 – E1
nur diskrete E – Zustände
sind möglich
vaughnyztheran.blogspot.com
Kurt Grießer OStD i.R,
49
uni-ulm.de
Kurt Grießer OStD i.R,
50
Atombau
Bohr‘sches Modell
h f = E 2 – E1
vaughnyztheran.blogspot.com
Kurt Grießer OStD i.R,
51
Bohr‘sches Atommodell - Absorption
Allgemeinwissen
Kurt Grießer OStD i.R,
52
Bohr‘sches Atommodell- Emission
Rücksprung
einen Augenblick später
Allgemeinwissen
Kurt Grießer OStD i.R,
53
Diese Linien lassen Rückschlüsse zu auf Eigenschaften des Sterns:
Ein chemisches Element in der Atmosphäre des Sterns
absorbiert auch im Laborversuch
jeweils die entsprechenden Frequenzen.
Allgemeinwissen
Kurt Grießer OStD i.R,
54
Atome der Atmosphäre absorbieren Einzellinien aus dem
kontinuierlichen Spektrum des glühenden Sternkörpers.
hmspeed.com
Kurt Grießer OStD i.R,
55
3 Spektrumsarten im Vergleich
hello-berlin.net
Kurt Grießer OStD i.R,
56
Beispiel: Wasserstoffatom
hmspeed.com
Kurt Grießer OStD i.R,
57
Termschema des Wasserstoffatoms
s.o.
Kurt Grießer OStD i.R,
58
Termschema des Wasserstoffatoms
s.o.
Kurt Grießer OStD i.R,
59
Balmerlinien im Visuellen
10 Å = 1 nm = 10 m-9
nbi.ku.dk
Kurt Grießer OStD i.R,
60
In diesem Gedankenversuch existieren die
soeben gezeigten 3 verschiedenen Spektren.
Glasbehälter mit heißem Wasserstoffgas
Absorption
Strahlungsquelle
Emission
Kontinuum
Kaler S.61
Kurt Grießer OStD i.R,
64
Absorption
Strahlungsquelle
Emission
Kontinuum
Kaler S.61
Kurt Grießer OStD i.R,
65
Beispiel: Wasserstoffatom
Berechnung der
Balmer-Linien
hmspeed.com
Kurt Grießer OStD i.R,
66
Berechnung von Hα
Geschw. = (Wellenlänge λ) x (Frequenz f)
c = λf
1 eV = 1,60 x 10-19 J
h = 6,63 x 10-34 J s
Energie ∝ Frequenz f
𝒄
E = hf= h
c = 3 x 108 m/s
E = Δn
(3,4 - 1,5) eV
𝝀
𝝀 =
𝒉𝒄
𝑬
(6,63 x 𝟏𝟎−𝟑𝟒 𝑱 s) x (3 x 𝟏𝟎𝟖 m/s)
λ =
(3,4 −1,5) x (1,60 x 𝟏𝟎−𝟏𝟗 J)
λ = 653 x 10 -9 m
Allgemeinwissen
Kurt Grießer OStD i.R,
67
Beispiel: Wasserstoffatom
Balmer - Serie
n1
-13,60
Hα
Hβ
Hγ
hmspeed.com
n2
-3,40
n3
n4
n5
-1,50 -0,89 -0,50 eV
λm
Δn
1,9 6,53E-07 2 n 3
2,51 4,94E-07 2 n 4
2,9 4,28E-07 2 n 5
h = 6,63E-34 J s
1 eV = 1,60E-19 J
c = 3,00E+08 m/s
Kurt Grießer OStD i.R,
68
428 nm
494 nm
Balmer - Serie
653 nm
Lyman – Serie: 122 nm; 103 nm ; 97 nm; 91 nm ; ……….. 91 nm
nbi.ku.dk
Kurt Grießer OStD i.R,
69
Beispiel: Wasserstoffatom
Lyman -Serie
n1
-13,60
n2
-3,40
Δ n
10,20
12,10
12,71
13,10
λm
1,22E-07
1,03E-07
9,76E-08
9,47E-08
Lα
Lβ
Lγ
Lδ
13,6 9,12E-08
hmspeed.com
n3
n4
n5
-1,50 -0,89 -0,50 eV
h = 6,63E-34 J s
1 eV = 1,60E-19 J s
c = 3,00E+08 m/s
Ionisationsgrenze
Kurt Grießer OStD i.R,
70
Vom Spektrum zur Zustandsgröße
1. Vision
2. Vision
Spektrum
Sterneigenschaft
Elemente
Spektralklassen
Spektralklassen
Radius
Masse
Alter
Allgemeinwissen
Leuchtkraft
HRD
Reihenfolge (S)
(Wasserstoff)
L über S oder T Temperatur
Kurt Grießer OStD i.R,
71
L
e
u
c
h
t
k
r
a
f
t
Allgemeinwissen
Kurt Grießer OStD i.R,
72
Weitere empirische Feststellung
hinsichtlich der Helligkeit:
Jedem Stern, dessen Entfernung d und dessen
scheinbare Helligkeit m bekannt sind, kann
rechnerisch eine „absolute Helligkeit M“ zugeordnet werden.
m - M = - 2,5 lg
Quadrat. Entfg Gesetz
𝑰𝟏
𝑰𝟐
Allgemeinwissen
=
𝟏𝟎 𝟐
𝒅
𝐼1
𝐼2
m: scheinbare Intensität I1
in d Parsec Entfernung
M: Intensität I2 in 10 pc Entfernung
M = m + 5 - 5 lg d
Kurt Grießer OStD i.R,
73
1/r2 - Lichtausbreitungsgesetz
E
E
𝐼1
=
𝐼2
𝐼2 =
Wikipedia
𝑟2
𝑟1
E
2
𝑟1 2
𝐼1
𝑟2
Kurt Grießer OStD i.R,
74
Entfernungsmodul - absolute Helligkeit
Weber-Fechner:
m - M = - 2,5 lg
𝑰𝟏
𝑰𝟐
=
m – M = -2,5lg
für ein- und denselben Stern
𝑰𝟏
𝑰𝟐
𝟏𝟎 𝟐
𝒅
𝟏𝟎 𝟐
𝒅
m: scheinbare Helligkeit in der Entfernung d Parsec
M: Helligkeit in 10 pc Entfernung
Helligkeit I eines Objekts nimmt mit
dem Quadrat der Entfernung ab.
m - M = - 5 lg
𝟏𝟎
𝒅
;
M = m + 5 - 5 lg d
m - M = - 5 + 5 lg d ;
m - M + 5 = 5 lg d ;
lg d =
Allgemeinwissen
𝒎 −𝑴+𝟓
𝟓
;
𝒎 −𝑴+𝟓
𝟓
d = 𝟏𝟎
Kurt Grießer OStD i.R,
75
Zuordnung der absoluten Helligkeit
m – M = - 2,5 lg
Entfernungsmodul:
𝟏𝟎 𝟐
𝒅
𝟏
M = m + 5 lg 10 + 5 lg
𝒅
M = m + 5 - 5 lg d
Wega: d = 8 pc
m = 0,04 mag
M = 0,5 mag
Bildung von Spektralklassen
Allgemeinwissen
Kurt Grießer OStD i.R,
76
Für die Mehrzahl der Sterne (der Hauptreihe) gilt
die empirische Feststellung:
Sterne mit gleichen Spektren haben
gleiche absolute Helligkeiten.
Das Spektrum eines Sterns der Hauptreihe und
seine absolute Helligkeit
sind 2 voneinander abhängige Eigenschaften eines Sterns.
Bildung von Spektralklassen
Allgemeinwissen
Kurt Grießer OStD i.R,
77
Spektraklasse, abs. Helligkeit, Temperatur
M
-5,7
-1,2
+1,9
+3,5
+5,1
+7,4
+12,3
noe-sternwarte.at/
Werte: Klett S 160
Kurt Grießer OStD i.R,
78
> absolute Helligkeit
Spektralklasse O
B
A
abs.Helligkeit -5,7 -1,2 1,9
abs. Heligkeit
-8
F
3,5
G
5,1
K
7,4
M
12,3
-5,7
-6
-4
-1,2
-2
0
1,9
2
3,5
5,1
4
6
7,4
8
10
12,3
12
14
16
O
B
A
F
G
K
M
Spektralklasse
Allgemeinwissen
Kurt Grießer OStD i.R,
79
Wasserstoff spielt eine
zentrale Rolle
noe-sternwarte.at/
Werte: Klett S 160
Kurt Grießer OStD i.R,
80
Beispiel: Wasserstoffatom
hmspeed.com
Kurt Grießer OStD i.R,
81
Reihenfolge O  M
H
He
Ca
www.lsw.uniheidelberg.de/users/mcamenzi
/HD_HRD.pdf
H
H
Mg
Kurt Grießer OStD i.R,
Na
82
H
He
H
H
5
4
1
2
3
6
7
8
9
10
11
13 ?
12
Ca
www.lsw.uniheidelberg.de/users/mcamenzi
/HD_HRD.pdf
Mg
Kurt Grießer OStD i.R,
Na
83
H
He
H
H
O
B
A
F
G
K
M
5
4
1
2
3
6
7
8
9
10
11
12
5
4
1
2
3
6
7
8
9
10
11
12
Ca
www.lsw.uniheidelberg.de/users/mcamenzi
/HD_HRD.pdf
Mg
Kurt Grießer OStD i.R,
Na
84
H
He
H
H
O
B
A
CDE
F
G
HIJ
K
L
M
5
4
1
2
3
6
7
8
9
10
11
12
Ca
www.lsw.uniheidelberg.de/users/mcamenzi
/HD_HRD.pdf
Mg
Kurt Grießer OStD i.R,
Na
85
https://lp.unigoettingen.de/get/bigimage/71
60
Kurt Grießer OStD i.R,
88
50 – 30
25 – 15
Reihenfolge
gegen
Temperatur
12 – 8
8–6
Tausend K
6–5
4
3,5
noe-sternwarte.at
Kurt Grießer OStD i.R,
90
Spektralklasse gegen Temperatur
Spektrakl
Temp
O
50000
B
20000
A
10000
F
7500
G
6000
K
4000
M
3500
Temp in K
60000
50000
40000
30000
20000
10000
0
O
LP Uni Goettingen astronomie
B
A
F
G
Kurt Grießer OStD i.R,
K
M
91
Zu jeder Spektralklasse gehört eine bestimmte Temperatur.
Die Spektralklasse macht keine Aussage über
die materielle Zusammensetzung
der Schicht, aus der die Strahlung kommt,
sondern über die materielle Zusammensetzung der Schicht,
die die Strahlung passiert hat.
Anordnung der Spektralklassen:
in Richtung abnehmender Temperatur
O
astrotreff.de
B
A
F
G
K
Kurt Grießer OStD i.R,
M
R
N
92
hmspeed.com
Kurt Grießer OStD i.R,
93
Henry Norris Russel
1877 - 1957
Um 1910 HRD
1922 Abkürzung der lat. Sternbildnamen
1929 Sonne besteht aus H und He
Vermutung Gamows: Kernfusion
Wikipedia
Kurt Grießer OStD i.R,
101
Mondkrater
Henry Norris Russell
wikipedia
Kurt Grießer OStD i.R,
102
Ejnar Hertzsprung
1873 - 1967
Absolute Helligkeit 1905
Temperatur-Leuchtkraft Diagramm 1909
internet
Kurt Grießer OStD i.R,
103
Der große Mondkrater
Hertzsprung liegt am Äquator
der Mondrückseite, östlich ihrer
Mitte. Er ist eine der größten
Ringstrukturen am Mond.
Selenografische Koordinaten
+11 bis -9°, Kratermitte 128°
West
Durchmesser etwa 500 km
Beckmann/Epperlein S. 126
Kurt Grießer OStD i.R,
104
Krater Hertzsprung
auf Mondrückseite
Beckmann/Epperlein S. 126
Kurt Grießer OStD i.R,
105
Russel Diagramm
1914
A+R 2013 H 6 S38
Kurt Grießer OStD i.R,
106
Russel Diagramm
1927
Beckmann/Epperlein S. 126
Kurt Grießer OStD i.R,
107
Russel Diagramm 1927
Gondolatsch-Zimmermann S.399
Kurt Grießer OStD i.R,
108
noticiasdelcosmos.com
Kurt Grießer OStD i.R,
109
Über-Riesen
Historisches
Diagramm 1950
Absolute visuelle Helligkeit
W. Gyllenberg,
Lund-Sternwarte,
Schweden
Riesen
Unter-Riesen
weiße Zwerge
Spektraltyp
Kaler S.99
Kurt Grießer OStD i.R,
110
Historisches Diagramm 1950:
Trennung zwischen Riesen und Zwergen
Hertzsprung – Lücke
Sprunghafter Übergang zum Riesenstadium
Unterrepräsentanz von kühlen K und M Sternen,
sowie weißen Zwergen
Aufnahmetechnik !
Die senkrechte Bänderung entsteht durch die
„digitale“ Einteilung in Spektralklassen
Kaler S.99
Kurt Grießer OStD i.R,
111
Hipparcos:
41.453 Sterne
der näheren
Sonnenumgebung
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Kurt Grießer OStD i.R,
112
Hipparcos:
41.453 Sterne
der näheren
Sonnenumgebung
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Kurt Grießer OStD i.R,
113
Für jeden Stern
gibt es einen Platz
im Diagramm.
Gleiche Plätze gleiche Eigenschaften
Beispiel: die Sonne
quantumredpill.wordpress.com
Kurt Grießer OStD i.R,
114
Für jeden Stern
gibt es einen Platz
im Diagramm.
Gleiche Plätze gleiche Eigenschaften
quantumredpill.wordpress.com
Kurt Grießer OStD i.R,
115
Diagramm mit Sterngrößen
univie.ac.at
Kurt Grießer OStD i.R,
116
HRD für die
100
nächsten Sterne
Cambridge Enzyklopedie S.36
Kurt Grießer OStD i.R,
117
Reihenfolge der Spektren
HRD für die
100
hellsten Sterne
Cambridge Enzyklopedie S.36
Kurt Grießer OStD i.R,
118
100 nächste Sterne
100 hellste Sterne
Reihenfolge der Spektren
Kaum helle Sterne in Sonnennähe; dafür auch die schwachen erfasst
Cambridge Enzyklopedie S.36
Kurt Grießer OStD i.R,
119
Sternkarte zu vorigen Diagrammen
Der Sternhimmel im Dezember/Januar
Astronomie + Raumfahrt
2001 Heft 6
de Boer: Lebenswege der Sterne
Kurt Grießer OStD i.R,
120
Beispiele einiger Sterne im HRD Diagramm
B 1 22.000 K
A 1 10.000 K
G 2 5.800 K
K 2 4.300 K
M 2 3.500 K
zum.de
Kurt Grießer OStD i.R,
121
Sterne
im
Effektive Temperatur
HRD
Beteigeuze
-5,3 mag
Spica
-3,6 mag
3.450 K
13.400
1.700
22.400 K
18.500 K
Arctur -0,3 mag
210
4.290 K
5.800 K
Sonne 4,8 mag
B
Karttunen - Kröger …
55.000
Sonnenleuchtkraft
Absolute Helligkeit
Wikipedia
Kurt Grießer OStD i.R,
G2
K2
M2
122
Für jeden Stern
gibt es einen Platz
im Diagramm.
Gleiche Plätze gleiche Eigenschaften
quantumredpill.wordpress.com
Kurt Grießer OStD i.R,
123
2 Fundamentale
empirische Folgerungen
Masse - Leuchtkraft - Beziehung
Masse – Radius - Beziehung
Allgemeinwissen
Kurt Grießer OStD i.R,
124
Masse - Leuchtkraft - Beziehung
B
y
𝟔
𝟏,𝟔
= 3,75
𝜟𝒚=6
A
𝜟 𝒙 = 1,6
-1,0
y = st x + b
Bergmann-Schäfer
Band 8 S.94
X
𝜟𝒚
𝒔𝒕 =
𝜟𝒙
Kurt Grießer OStD i.R,
b = 0 (oEdA)
Parallelverschiebung
125
Masse - Leuchtkraft - Beziehung
y = st x
y
=
3,8 x
lg L/L = 3,8 lg M/M
lg L/L = lg (M/M)3,8
L/L = (M/M)3,8
Literaturwert
Unsöld - Baschek
Bergmann-Schäfer
Band 8 S.94
Lg L/L = 3,8 lg M/M + 0,08
Kurt Grießer OStD i.R,
126
Beziehun
Masse -gLeuchtkraft
- Beziehung
Graphik
2
𝟏,𝟑
𝟎,𝟑
B
= 4,3
Δ y = 1,3 ___
A
Δ x = 0, 3
-1,0
y = st x + b
Bergmann-Schäfer
Band 8 S.94
𝜟𝒚
𝒔𝒕 =
𝜟𝒙
Kurt Grießer OStD i.R,
b = 0 (oEdA)
Parallelverschiebung
127
Masse - Leuchtkraft - Beziehung
Y = 4,3 x
Lg L/L = 4,3 lg M/M
Lg L/L = lg (M/M)4,3
L/L = (M/M)4,3
Literaturwert
Bergmann-Schäfer
Band 8 S.94
(M/M)4,5
Kurt Grießer OStD i.R,
128
Masse - Radius - Beziehung
Allgemeinwissen
Kurt Grießer OStD i.R,
129
Masse - Radius - Beziehung
y
Bedeckungsveränderliche
B
st =
0,5
0,9
= 0,44
Δy = 0,5
A
Δx = 0,9
X
y = st x + b
Weigert – Wendker S. 102
st =
Δ𝑦
Δ𝑥
Kurt Grießer OStD i.R,
b = 0 oEdA
Parallelverschiebung
130
Masse - Radius - Beziehung
y = 0,44
Lg R/R = 0,44 lg M/M
Lg R/R = lg (M/M)0,44
R/R = (M/M)0,44
Literaturwert
Weigerft – Wendker S.102
(M/M)0,6
Kurt Grießer OStD i.R,
131
Diese Abhängigkeiten müssen einen tieferen Grund haben.
Masse
Leuchtkraft
Leuchtkraft
Spektralklasse
Masse
Spektralklasse
Masse
Radius
Radius
Spektralklasse
Spektralklasse
Temperatursequenz
Masse
Temperatursequenz
Allgemeinwissen
Kurt Grießer OStD i.R,
132
Diese Abhängigkeiten müssen einen tieferen Grund haben.
Masse
Leuchtkraft
Leuchtkraft
Spektralklasse
Masse
Spektralklasse
Masse
Radius
Radius
Spektralklasse
Spektralklasse
Temperatursequenz
Masse
Temperatursequenz
Schwarzkörperstrahlung
Allgemeinwissen
Kurt Grießer OStD i.R,
133
Sonne bestrahlt die Erde
Erde erwärmt sich*
Erde strahlt ihrerseits
wieder Energie ab
Gleichgewichtszustand:
zugestrahlte Energie
abzüglich reflekt. Energie*
me-lrt.de
=
Kurt Grießer OStD i.R,
von der Erde
abgestrahlte Energie
134
Schwarzkörperstrahlung
didaktikonline.physik.unimuenchen.de
Kurt Grießer OStD i.R,
135
Wikipedia
Kurt Grießer OStD i.R,
136
Schwarzkörperstrahlung
Jeder Körper gibt an seine Umgebung eine
elektromagnetische Strahlung ab,
die nur von seiner Temperatur abhängig ist.
Auch bei tieferen (Raum)Temperaturen gültiges Gesetz.
didaktikonline.physik.unimuenchen.de
Kurt Grießer OStD i.R,
137
Dieses Strahlungsgleichgewicht gilt für
jeden Körper
zwischen ihm
und seiner Umgebung.
Allgemeinwissen
Kurt Grießer OStD i.R,
138
Schwarzkörperstrahlung
niedere
höhere
Temperatur
didaktikonline.physik.unimuenchen.de
Kurt Grießer OStD i.R,
139
Schwarzkörperstrahlung
schwarze Fenster
eines Hauses
didaktikonline.physik.unimuenchen.de
Blitzlicht
rote Augen - Effekt
Kurt Grießer OStD i.R,
141
Blitzlicht
rote Augen - Effekt
didaktikonline.physik.unimuenchen.de
Kurt Grießer OStD i.R,
142
Schwarzkörperstrahlung
ideale
Schwarzkörperstrahlung
Wikipedia
Kurt Grießer OStD i.R,
143
ideale
Schwarzkörperstrahlung
daten.didaktikchemie.unibayreuth.de
Kurt Grießer OStD i.R,
144
Sonne als Schwarzkörperstrahler
ideale Schwarzkörperstrahlung
Temperatur 5.800 K
extraterrestrische Sonnenstrahlung
Satellitenmessung
terrestrische Sonnenstrahlung
de.wikibooks.org
Kurt Grießer OStD i.R,
145
Die Sonne als Schwarz-Körper-Strahler
Sonne
5.000 K
3.000 K
8.000 K
www.lsw.uniheidelberg.de/users/mcamenzi
/HD_HRD.pdf
Kurt Grießer OStD i.R,
146
Die Sonne als Schwarz-Körper-Strahler
tf.uni-kiel.de
Kurt Grießer OStD i.R,
147
Schwarzkörperstrahlung: Leuchtkraft
Planck‘sche Strahlung
E(λ,T) = 2 𝝅
𝒄² 𝒉
𝝀𝟓
𝟏
𝒄𝒉
− 𝟏
𝒆𝒌𝑻𝝀
Stephan – Boltzmann
E = A σ T4
L = 4 π R² σ T4
Daraus wird eine Oberflächen - Sterntemperatur Teff
definiert:
Teff ist diejenige Temperatur eines
gleichgroßen Schwarzkörperstrahlers,
der die gleiche Strahlungsleistung wie der Stern abgibt.
Allgemeinwissen
Kurt Grießer OStD i.R,
148
Temperatur Teff der Sonne:
L = 4 π R² σ T4
Teff =
𝟒
𝑳
4 π 𝝈 R²
L = 3,82E+26 W
Teff = 5.768 K
R = 6,96E+08 m
σ = 5,67E-08 W-2K-4
R² = 4,84E+17 m²
Die Sonne strahlt die Energie eines
„Schwarzen Strahlers“ gleicher Größe (Oberfläche)
und der Temperatur 5.800 K ab.
Allgemeinwissen
Kurt Grießer OStD i.R,
149
Stephan – Boltzmann‘sches Gesetz
Planck‘sche Strahlung
E(λ,T) = 2 𝝅
𝒄² 𝒉
𝝀𝟓
𝟏
λ =
E(T)dλ = 2 π 𝑐² ℎ
𝑘 𝑇 5 𝑥5
𝑐² ℎ 𝑒 𝑥 −1
𝑘 𝑇 5 ∞ 𝑥5
0 𝑒 𝑥 −1
𝑐² ℎ
𝑑λ
E(T)dλ = 2 π 𝑐² ℎ
Gondolatsch/Groschopf S.319.
𝑘 𝑇 5 ∞ 𝑥 5 𝑐ℎ 1
0 𝑒 𝑥 −1 𝑘𝑇 𝑥²
𝑐² ℎ
𝑘 𝑇 4 ∞ 𝑥3
0 𝑒 𝑥 −1
𝑐² ℎ
𝑐ℎ
𝑘𝑇
λ =
5
𝑐ℎ
𝑘𝑇𝑥
1
𝑥5
Von der Integrationsvariablen λ
zur I-Variablen x:
𝑐ℎ
E(T)dλ = 2 π 𝑐² ℎ
= 𝑥;
5
𝒄𝒉
− 𝟏
𝒆𝒌𝑻𝝀
E(λ,T) = 2 π 𝑐² ℎ
𝑐ℎ
𝑘𝑇λ
Ersetze
dx
x = 𝑘𝑇λ;
𝑑𝑥
𝑑λ
𝑐ℎ
= - 𝑘 𝑇 λ² ; dλ = 𝑘𝑇 (𝑐ℎ)² 1
𝑘 𝑇 λ²
𝑐ℎ
dx
𝑐ℎ 1
𝑥²
dλ = - 𝑐ℎ (𝑘𝑇)² 𝑥² dx =𝑘𝑇
dx
dx
Kurt Grießer OStD i.R,
150
Stephan – Boltzmann‘sches Gesetz
E(T) = 2 π 𝑐² ℎ
𝑘 𝑇 4 ∞ 𝑥3
0 𝑒 𝑥 −1
𝑐² ℎ
E(T) = 2 π 𝑐² ℎ
𝑘 4
𝑐² ℎ
𝑇4
dx
∞ 𝑥3
0 𝑒 𝑥 −1
dx
Konstante Werte
E(T) ∝ 𝑇 4
E(T) = σ 𝑇 4
s.o.
Kurt Grießer OStD i.R,
151
Sternradien im HRD
Stefan- Boltzmann - Gesetz für einen Stern und die Sonne 
L = 4 π R² σ
𝐿
𝐿
T4
𝐿
𝐿
𝑳
𝑳
Herrmann, Astrophysik
Aufg. 120

=
Kurt Grießer OStD i.R,
=
4 π 𝑅² σ 𝑇 4
4 π 𝑅² σ 𝑇4
=
4 π 𝑅² σ 𝑇 4
4 π 𝑅² σ 𝑇4
𝑹
𝑹

𝟐
∗
𝑻
𝟒
𝑻

152
Sternradien im HRD
Stefan- Boltzmann - Gesetz für einen Stern und die Sonne 
𝑳
L = 4 π R² σ T4
𝑳
=

y
lg
L(L)
x
𝑳
𝑳

y
T(K)
Herrmann, Astrophysik
Aufg. 120
𝑹
𝑹
𝟐

= 2 lg
=
∗
𝑹
𝑹

𝑻
𝟒
𝑻

+ 4 lg
𝑻
𝑻

r + 4x
jeweils in log - Skala
Kurt Grießer OStD i.R,
153
Sternradien im HRD: Berechnung
𝐿
𝐿
1.000.000
Reihenfolge der Spektren
100.000
=
𝐿
=
4 π 𝑅² σ 𝑇4
4 π 𝑅² σ 𝑇4
𝑅
𝑅
2
𝑇
10.000 L
𝐿
1.000
Lg 𝐿
= 2 lg 𝑅 + 4 lg 𝑇




𝑇
4

𝐿

𝑅
𝑇
100
Y
=
const + st x
10
R = const
1 L
0,1
4
0,01
10.000 K
1.000 K
100.000 K
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Kurt Grießer OStD i.R,
Parallele Geraden,
da st (4) für jeweils
konstante R gleich
154
Sternradien im HRD: Größenordnung
Achsenmaßstab
1.000.000
gängige Werte
Reihenfolge der Spektren
100.000
10.000
𝟏𝟎𝟒𝑳
𝑳

L
1.000

𝟐
𝟏𝟎 𝑻 𝟒
𝑻

Wertebereiche:
100
decken vorkommende
Zustandsgrößen L, T
auf einer log – Skala ab.
10
1
=
𝑹
𝑹
L
100.000 K > T > 1.000 K
0,1
0,01 L < L < 100.000 L
0,01
100.000 K
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
10.000 K
Kurt Grießer OStD i.R,
1.000 K
155
Sternradien im HRD mit Temperaturen
1.000.0000
Reihenfolge der Spektren
100.000
𝐿
𝐿
10.000
=

𝑅
𝑅
2
𝑇
𝑇

4

1.000
𝐿
𝑅
𝑇
Lg 𝐿
= 2 lg 𝑅 + 4 lg 𝑇



100
10
R = const
1
Y = const + st x
0,1
0,01
32.000 K
4,5
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
6.300 K 2.500 K
1.000 k
3,4
3,8
Kurt Grießer OStD i.R,
Parallele Geraden,
da st für alle R gleich
156
Die Sonne
Reihenfolge der Spektren
𝐿
𝐿
=

𝑅
𝑅
2
𝑇

𝐿
𝑇
4

𝑅
𝑇
Lg 𝐿
= 2 lg 𝑅 + 4 lg 𝑇



R = const
1 L
Y = const + st x
3,5
lg T
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Parallele Geraden,
da st für alle R gleich
lg 5.800 = 3,76
Kurt Grießer OStD i.R,
157
Wo liegt in diesem Diagramm ein Stern mit
Sonnen - Radius R
und
10 facher Sonnentemperatur (58.000 K) ?
Aufgabe
Kurt Grießer OStD i.R,
158
100.000
10.000 L
𝟏𝟎𝟒𝑳
𝑳

Reihenfolge der Spektren
𝐿
𝐿

1.000
100

𝐿
=
=
𝟐
𝑹
𝑹

𝑅
𝑅
𝟏𝟎 𝑻 𝟒
𝑻

2
𝑇
𝑇

4

𝑅
𝑇
Lg 𝐿
= 2 lg 𝑅 + 4 lg 𝑇



x 104
R = const, parallele Geraden
10
Y = const + st x
x 10
1 L
Ein Stern mit 100facher
Sonnenleuchtkraft und
Sonnenradius ist
lg 4,28 ≈ 𝟏𝟗. 𝟎𝟎𝟎 𝑲 heiß.
0,1
0,01
58.000 K
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
4,28
19.000 K
3,5
5.800 K
Kurt Grießer OStD i.R,
1.000 K
159
Wo liegt ein Stern mit Sonnentemperatur
aber 10 fachem Sonnenradius ?
Aufgabe
Kurt Grießer OStD i.R,
160
100.000
𝟏𝟎𝟎𝑳
𝑳

Reihenfolge der Spektren
𝐿
𝐿
10.000 L
=

=
𝟏𝟎𝑹 𝟐
𝑹

𝑅
𝑅
𝑻
𝑻
2

𝑇
𝑇

𝟒
4

1.000
100
𝐿
10
𝑅
𝑇
Lg 𝐿
= 2 lg 𝑅 + 4 lg 𝑇



 10 R
100 L
R = const
1 L
Y = const + st x
0,1
Parallele Geraden,
da st für alle R gleich
0,01
1.000 K
100.000 K
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Kurt Grießer OStD i.R,
161
Auf welcher Geraden liegen Sterne mit
Sonnentemperatur und 50 fachem Sonnenradius ?
Aufgabe
Kurt Grießer OStD i.R,
162
Masse - Temperatur - Beziehung
und
Masse - Radius - Beziehung
Allgemeinwissen
Kurt Grießer OStD i.R,
170
Masse - Temperatur - Beziehung
Bedeckungsveränderliche
L/L =
𝐑 𝟐
𝐑
𝐓 𝟒
𝐓
L/L = (M/M)3,5
L/L = (M/M)3,5
R/R = (M/M)0,6
(M/M)3,5 = (M/M)1,2 (T/T )4
(M/M)3,5 - 1,2 = (T/T )4 ;
(M/M)2,3 = (T/T )4
T/T = (M/M)0,58
Weigerft – Wendker S.102
Kurt Grießer OStD i.R,
171
Masse - Radius - Beziehung
T/T = (M/M)0,58
L/L =
𝐑 𝟐
𝐑
𝐓 𝟒
𝐓
L/L = (M/M)3,5
L/L = (M/M)3,5
R/R = (M/M)0,6
(M/M)3,5 = (R/R)² (M/M)0,58
(M/M)3,5 – 2,3 = (R/R)²
𝟒
(M/M)1,2 = (R/R)²
(R/R) = (M/M)0,58
Weigerft – Wendker S.102
Kurt Grießer OStD i.R,
172
Verweilzeit auf der Hauptreihe
Verweilzeit auf der Hauptreihe
Allgemeinwissen
Kurt Grießer OStD i.R,
173
Verweilzeit auf der Hauptreihe Wasserstoff-Fusion im Kern
Masse des Sterns: M,
Fusion 10%
davon 70% Wasserstoff;
Fusionierte Masse: 0,07 M
Leuchtkraft L in [J/s] oder Watt
Fusionsrate: 6,13x 1014 J/kg
Verweilzeit τ in [s]
Abgestrahlte Energie in der Verweilzeit L τ = 0,07 M 6,13x 1014 J/kg
τ = 0,43 x 1014 J/kg
M
𝑳
Masse-Leuchtkraft - Beziehung
Gondolatsch-Groschopf II
S.404
Kurt Grießer OStD i.R,
𝑳
M
=
M
𝐿
3
174
𝑳
M
= M
𝑳

𝑳
M
M
M
𝑳
𝐿
M
𝐿
𝟑
Verweilzeit auf der Hauptreihe
Wasserstoff-Fusion im Kern
M
x
M
M
= M

M
= M

𝟐
τ = 0,43 x 1014 J/kg
𝑳
M
𝑳
𝟑,𝟖 𝒙 𝟏𝟎𝟐𝟔 𝑱/𝒔
𝟐 𝒙𝟏𝟎𝟑𝟎 𝒌𝒈
=
𝑳
−𝟐
τ = 0,43 x
M
M
M
= M

𝒌𝒈 𝒔
𝟓, 𝟐𝟔𝒙𝟏𝟎³ 𝑱
1014
−𝟐
M
M
−𝟐
τ = 𝟐, 𝟐𝟔 𝒙
𝒌𝒈 𝒔
J/kg 𝟓, 𝟐𝟔𝒙𝟏𝟎³ 𝑱
𝟏𝟎𝟏𝟕
M
𝒔 M

−𝟐
M
τ = 7,16 x 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆
M
Gondolatsch-Groschopf II
S.404
Kurt Grießer OStD i.R,
M
M
−𝟐
175
−𝟐
𝑳
M
= M
𝑳

𝑳
M
M
𝐿
M
𝑳
M
𝑳
M
𝑳
𝐿
M
𝟑,𝟓
M
= M

M
= M

𝟑,𝟖𝒙𝟏𝟎𝟐𝟔𝑱/𝒔
𝟐 𝒙𝟏𝟎𝟑𝟎𝒌𝒈
=
x
Verweilzeit auf der Hauptreihe
Wasserstoff-Fusion im Kern
M
M
𝟐,𝟓
−𝟐,𝟓
M
= M

𝒌𝒈 𝒔
𝟓, 𝟐𝟔𝒙𝟏𝟎³ 𝑱
τ = 0,43 x 1014 J/kg
τ = 0,43 x
−𝟐,𝟓
M
M
−𝟐,𝟓
M
𝑳
𝒌𝒈 𝒔
1014 J/kg 𝟓, 𝟐𝟔𝒙𝟏𝟎³ 𝑱
M
τ = 𝟐, 𝟐𝟔 𝒙 𝟏𝟎𝟏𝟕 𝒔 M

M
M
−𝟐,𝟓
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆
M
Gondolatsch-Groschopf II
S.404
Kurt Grießer OStD i.R,
−𝟐,𝟓
−𝟐,𝟓
176
Verweilzeit auf der Hauptreihe
7,16E+09
M/M
0,01
0,1
1
2
3
5
10
20
50
100
s.o.
(M/M)²
1,00E+04
1,00E+02
1,00E+00
2,50E-01
1,11E-01
4,00E-02
1,00E-02
2,50E-03
4,00E-04
1,00E-04
7,2E+13
7,2E+11
7,2E+09
1,8E+09
8,0E+08
2,9E+08
7,2E+07
1,8E+07
2,9E+06
7,2E+05
Kurt Grießer OStD i.R,
τ
72
720
7,2
1,8
800
290
72
18
2,9
720
Billio
Millia
Millio
Tausend
177
Verweilzeit auf der Hauptreihe
18
Millionen
Jahre
72
290
Milliarden
1,8 Jahre
7,2
4,8 mag
29
G 2 5.800 K 720
Gondolatsch-Groschopf II
S.401
M
0,1
0,5
1
2
3
5
10
20
Kurt Grießer OStD i.R,
Verweilzeit τ auf HR
7,20E+11 720
2,90E+10
29
Millia J
7,20E+09 7,2
1,80E+09 1,8
8,00E+08 800
2,90E+08 290
Millio J
7,20E+07
72
1,80E+07
18
178
Verweilzeit auf der Hauptreihe
7,16E+09
M/M
0,01
0,1
1
2
3
5
10
20
50
100
s.o.
(M/M)2,5
1,00E+05
3,16E+02
1,00E+00
1,77E-01
6,42E-02
1,79E-02
3,16E-03
5,59E-04
5,66E-05
1,00E-05
7,2E+14
2,3E+12
7,2E+09
1,3E+09
4,6E+08
1,3E+08
2,3E+07
4,0E+06
4,1E+05
7,2E+04
Kurt Grießer OStD i.R,
τ
72
720
7,2
1,8
460
130
23
4
2,9
720
Billio
Millia
Millio
Tausend
179
Verweilzeit auf der Hauptreihe
www.zum.de/Faecher/A/Sa/ST
ERNE/hrd
Kurt Grießer OStD i.R,
180
Verweilzeit auf der Hauptreihe
M
τ
0,1
0,5
1
2
3
5
10
20
7,2E+11
2,9E+10
7,2E+09
1,8E+09
8,0E+08
2,9E+08
7,2E+07
1,8E+07
720
29
7,2
1,8
800
290
72
18
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

s.o.
M
τ
Milliarden Jahre
Millionen Jahre
−𝟐
𝟑
2.300
41
7,2
13
460
130
23
4
2,3E+12
4,1E+10
7,2E+09
1,3E+09
4,6E+08
1,3E+08
2,3E+07
4,0E+06
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

Kurt Grießer OStD i.R,
0,1
0,5
1
2
3
5
10
20
−𝟐,𝟓
𝟑,𝟓
181
Verweilzeit auf der Hauptreihe
M
τ
0,1
0,5
1
2
3
5
10
20
7,2E+12
5,7E+10
7,2E+09
9,0E+08
2,7E+08
5,7E+07
7,2E+06
9,0E+05
720
57
7,2
0,9
270
57
7
0,9
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

s.o.
M
τ
Milliarden Jahre
Millionen Jahre
−𝟑
𝟒
2.300
81
7,2
0,6
150
26
2,3
0,4
2,3E+13
8,1E+10
7,2E+09
6,3E+08
1,5E+08
2,6E+07
2,3E+06
2,0E+05
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

Kurt Grießer OStD i.R,
0,1
0,5
1
2
3
5
10
20
−𝟑,𝟓
𝟒,𝟓
182
Verweilzeit auf der Hauptreihe
M
τ
0,1
0,5
1
2
3
5
10
20
50
7,2E+11
2,9E+10
7,2E+09
1,8E+09
8,0E+08
2,9E+08
7,2E+07
1,8E+07
2,9E+06
720
29
7,2
1,8
800
290
72
18
3
Milliarden Jahre
Millionen Jahre
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

s.0.
M
τ
−𝟐
𝟑
2.300
41
7,2
13
460
130
23
4
0,45
2,3E+12
4,1E+10
7,2E+09
1,3E+09
4,6E+08
1,3E+08
2,3E+07
4,0E+06
4,1E+05
M
τ = 𝟕, 𝟏𝟔 𝒙 𝟏𝟎𝟗 𝑱𝒂𝒉𝒓𝒆 M

𝑳
M
= M
𝑳

Kurt Grießer OStD i.R,
0,1
0,5
1
2
3
5
10
20
50
−𝟐,𝟓
𝟑,𝟓
183
Die Masse als Eingangsparameter
bei der Sternentstehung
Allgemeinwissen
Kurt Grießer OStD i.R,
185
Sterne
der Hauptreihe
Wasserstoff-Helium-Wolke
der Masse M
Zustandsgrößen
(Hauptreihe)
hängen nur von
der Sternmasse ab.
Leuchtkraft
absolute Helligkeit
Mio.
Mrd.
Spektrum
Oberflächentemperatur
Verweilzeit
Radius
Wikipedia
Kurt Grießer OStD i.R,
186
Verweilzeit: Sonne
Millionen
Jahre
18
M = 1 M
72
290
1,8
Milliarden
Jahre
7,2
29
M = 4,8 mag
L = 1 L
T = 5.800 K
720
G2
FI = 0,65 mag
τ = 7,2 x 109 a
Gondolatsch-Groschopf II
S.401
Kurt Grießer OStD i.R,
187
Verweilzeit: 2 M
Millionen
Jahre
18
M = 2 M
72
M = 2,5 mag
290
1,8
Milliarden
Jahre
7,2
29
L = 10 L
T = 8.000 K
720
A8
FI = 0,25 mag
τ = 1,8 x 109 a
Gondolatsch-Groschopf II
S.401
Kurt Grießer OStD i.R,
188
Stern mit 2 Sonnenmassen
M = 2 M
T = 8.000 K
lg T = 3,9
L = 10 L
lg L = 1
R ≈ 𝟏, 𝟓 𝑹

s.o.
Kurt Grießer OStD i.R,
189
Stern mit
5 Sonnenmassen
Millionen
Jahre
18
72
M = 5 M
290
1,8
Milliarden
Jahre
7,2
M = 0,0 mag
L = 100 L
29
720
T = 12.000 K
B7
FI = - 0,1 mag
Gondolatsch-Groschopf II
S.401
τ = 290 x 106 a
Kurt Grießer OStD i.R,
190
Sternradien für 2 und 5 Sonnenmassen
M = 2 M
T = 8.000 K
lg T = 3,9
L = 10 L
lg L = 1
R ≈ 𝟏, 𝟓 𝑹

M = 5 M

T = 12.000 K
lg T = 4,1
L = 100 L
lg L = 2
R ≈ 𝟐 𝑹
s.0.
Kurt Grießer OStD i.R,
191
Nachteil der Spektralklassifikation
Nur bis 10(?) mag scheinbare Helligkeit Spektralklasse bestimmbar.
Schwächere Sterne in größeren Entfernungen
werden nicht mehr erfasst.
Schwarzkörperstrahlung
der Sterne hilft weiter.
Vergleich mit dem Auge
didaktikonline.physik.unimuenchen.de
Kurt Grießer OStD i.R,
192
3 verschiedene Skalen:
Spektralklassen, Temperatur, Farbindex
Gondolatsch-Groschopf II
S.401
Kurt Grießer OStD i.R,
193
Statt Spektralklasse: Farbindex
Die Spektralklassifikation hat einen
großen Nachteil. Sternspektren
können nur bis 11 (?) mag Helligkeit
klassifiziert werden.
Schwächere Sterne und das ist der größte Teil,
sind in das HRD Diagramm nicht integrierbar.
Lösung: Änderung des Aufnahmeverfahrens
Allgemeinwissen
Kurt Grießer OStD i.R,
196
Auge
Tageslicht:
starke Intensität
Nachtsicht:
schwache Intensität
bmo.physik.uni-muenchen.de
Farbiges Sehen
möglich
Hell - dunkel - Sehen
In der Nacht sind alle
Katzen grau.
Kurt Grießer OStD i.R,
AstroAufnahme
Spektrum
Farbindex
197
350 nm < B < 550 nm
450 nm
475 nm < V < 675 nm
Farben - Helligkeits - Diagramm: Blauhelligkeit
filmscanner.info
Kurt Grießer OStD i.R,
198
475 nm < V < 675 nm
575 nm
Farben - Helligkeits - Diagramm: Visuelle Helligkeit
filmscanner.info
Kurt Grießer OStD i.R,
199
350 nm < B < 550 nm
450 nm
Farbindex
B - V = mB - mV
475 nm < V < 675 nm
575 nm
Farben - Helligkeits - Diagramm
filmscanner.info
Kurt Grießer OStD i.R,
200
350 nm < B < 550 nm
450 nm
Farbindex
475 nm < V < 675 nm
575 nm
B -- V = mB - mV
Farben - Helligkeits - Diagramm
filmscanner.info
Kurt Grießer OStD i.R,
201
Farbindex
350 nm < B < 550 nm
475 nm < V < 675 nm
B - V
Farben - Helligkeits - Diagramm: Farbindex (7000 K)
filmscanner.info
Kurt Grießer OStD i.R,
202
B - V
Ein Maß für die Steigung der
zugehörenden Planck-Kurve
d.h.
ein Maß für die Temperatur
des zugehörenden Sterns
Farben - Helligkeits - Diagramm für 3 versch. Temperaturen
filmscanner.info
Kurt Grießer OStD i.R,
203
Der Farbindex ist von der Entfernung unabhängig:
m - M = - 2,5 lg
𝟏𝟎 𝟐
𝒓
m – M = - 5 lg10 - 5 lg
𝟏
𝒓
m = M – 5 + 5lgr
Die Beziehung gilt auch für Teilhelligkeiten:
mB = MB – 5 + 5lgr
mV = MV – 5 + 5lgr
mB - mV = MB - MV
Allgemeinwissen
Kurt Grießer OStD i.R,
204
Vorteile des Farbindex gegenüber der Spektralklassifikation:
Von der Entfernung unabhängig.
Noch messbar für schwache Objekte,
die keine Spektralzuordnung mehr ermöglichen.
Systematisierbar,
d.h. er ist eindeutig, stetig einer Temperatur zuzuordnen.
Statt mit absoluten kann mit
scheinbaren Helligkeiten gearbeitet werden.
Farben - Helligkeits - Diagramm
filmscanner.info
Kurt Grießer OStD i.R,
211
Hipparcos:
41.453 Sterne
der näheren
Sonnenumgebung
Farben-Helligkeits-Diagramm
FHD
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
Kurt Grießer OStD i.R,
212
W. Gyllenberg,
Lund-Sternwarte,
Schweden
Absolute visuelle Helligkeit
Historisches
Diagramm 1950
Hertzsprung – Russel –
Diagramm
Spektraltyp
Kaler S.99
Kurt Grießer OStD i.R,
213
HRD
Spektralklasse
http://www.astro.unibonn.de/%7Edeboer/sterne/hr
dtxt.html
FHD
Farbindex
Kurt Grießer OStD i.R,
THD
Temperatur K
214
Leuchtkraftklassen
Quelle
Kurt Grießer OStD i.R,
215
abnehmende Temperatur
Alle Sterne der
Hauptreihe
dehnen sich nach
dem
Ende der
Verweilzeit aus.
hohe
Leuchtkraft
Temperatur nimmt ab.
Dennoch
hohe Leuchtkraft.
Große Radien
Wikipedia
Kurt Grießer OStD i.R,
216
Leuchtkraftklassen
Stefan – Boltzmann:
L = 4 π R² σ T4
Die Leuchtkraft hängt
vom Radius und der Temperatur
der Sternoberfläche ab
Quelle
Kurt Grießer OStD i.R,
217
Leuchtkraftklassen
Stefan – Boltzmann:
L = 4 π R² σ T4
4 π R²(D) σ T4(D) = 4 π R²(B) σ T4(B)
R²(D) T4(D) = R²(B) T4(B)
R²(D) 11.000K4 = R²(B) 3.500K4
R(D) 11.000² = R(B) 3.500²
R(B) ≈ 𝟏𝟎 𝐑(𝐃)
Die Leuchtkraft hängt
vom Radius und der Temperatur
der Sternoberfläche ab
Allgemeinwissen
Kurt Grießer OStD i.R,
218
Hertzsprung – Russel – Diagramm (HRD)
L/L⊙
Regulus ist ein Hauptreihenstern B7 mit
M ≈ – 0,6 und L* = L / L⊙ ≈ 100
und T ≈ 13000 K
mM
r
r
m  M  5  lg

 10 5
10 pc
10 pc
10000
100
 r  10 pc 10
R
R 

R
*
1
0,01
0,0001
1,36  (  0,6)
5
 25 pc
2
L T
 2 
L
T
100 58002

2
2
1 13000
Denebola ist ein Hauptreihenstern A3 mit m = 2,14.
Bestimmen Sie näherungsweise die Entfernung
dieses Sterns. (Spektroskopische Entfernungsbestimmung!)
M  1,5  m  M  5  lg
Welche Eigenschaften von Regulus zeigt das HRD?
Bestimmen Sie die Entfernung von Regulus und den
relativen Radius, wenn man m = 1,36 kennt!
r

10 pc
mM
2,14  1,5
r
5
 10
 r  10 pc 10 5  13pc
10 pc
Hertzsprung – Russel – Diagramm (HRD)
5  M1  M 2   2,5  lg
M= -5
M= 0
lg
M = 10
Auf der senkrechten Achse kann man statt M auch L auftragen.
Zeigen Sie, dass zur 100-fachen Leuchtkraft eine um 5 kleinere
absolute Helligkeit gehört.
Schätzen Sie den Sternradius von Arktur ab!

L1
L
1
  2  1  10  2 
L2
L2
100
L    A  T 4    4  R 2  T 4
also
M = 4,8
L1
L2
R
R
R 

R
*
L
T2
2
L T
 2 
L
T
100 58002

 19
1 42002
Leuchtkraftklassen
Stefan – Boltzmann:
L = 4 π R² σ T4
Die Leuchtkraft hängt
vom Radius und der Temperatur
der Sternoberfläche ab
s.0.
Kurt Grießer OStD i.R,
221
Gravitationsbeschleunigung
Reihenfolge der Spektren
Probemasse m x Beschleunigung g = Gravitationskraft
mg =
𝒎𝑴𝑮
𝑹²
𝒈
𝒈
𝒈
𝒈

g =
=
=
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
𝑴𝑮
𝑹²
𝑴 𝑮 𝑹 ²
𝑹 ² 𝑴𝑮
𝑴
𝑴

𝑹 𝟐
𝑹
𝒈 =
Kurt Grießer OStD i.R,
𝑴
𝑴

𝑹 𝟐
𝑹
g
222
Gravitationsbeschleunigung
Reihenfolge der Spektren
𝒈 =
𝑴
𝑴

𝑹 𝟐
𝑹
g
Bei konstanter Masse M in Sonnenmassen
nimmt die Gravitationsbeschleunigung g
mit
www.astro.unibonn.de/~deboer/sterne/hrdtxt
.html
𝟏
𝑹²
𝐢𝐧 𝐒𝐨𝐧𝐧𝐞𝐧𝐫𝐚𝐝𝐢𝐞𝐧 𝐚𝐛.
Kurt Grießer OStD i.R,
223
Gravitationsbeschleunigung
𝒎𝑴𝑮
𝑹²
𝑴𝑮
𝑹²
mg =
g =
Reihenfolge der Spektren
g/1.000.000
g/10.000
g/100
www.astro.unibonn.de/~Allgemeinwissen
Kurt Grießer OStD i.R,
𝑴
𝑴
𝒈 =

S
t
e
r
n
r
a
d
i
u
s
𝑹 𝟐
𝑹
g
G
a
s
d
r
u
c
k
224
EmissionsSpektrum
Kontinuum
http://www.astro.uu.se/~ulrike
/Spektroskopie/PPT/Druckverb
reiterung.GIF
Kurt Grießer OStD i.R,
225
Gasdruck
nimmt
zu
astro.uu.se
Kurt Grießer OStD i.R,
226
Leuchtkraftklassen
Stefan – Boltzmann:
L = 4 π R² σ T4
I
II
V
Wikipedia
Kurt Grießer OStD i.R,
227
Balmer - Serie
I
III
IV
V
entscheidet über die
Leuchtkraftklasse
Wikipedia
Kurt Grießer OStD i.R,
228
Damit hat jeder,
aber auch wirklich
jeder Stern seinen
eindeutigen
Platz
im Diagramm,
der seinem
Zustand entspricht.
Wikipedia
Kurt Grießer OStD i.R,
229
Damit hat jeder,
aber auch wirklich
jeder Stern seinen
eindeutigen
Platz
im Diagramm,
der seinem
Zustand entspricht.
Wikipedia
Kurt Grießer OStD i.R,
230
HRD bzw. FHD
von
Sternhaufen
Quelle
Kurt Grießer OStD i.R,
231
Eigenschaften eines Sternhaufens
Alle Mitglieder eines Haufens haben
• etwa gleiches Alter,
gemessen an der „Lebenserwartung“ eines Sterns.
• gleiche Entfernung,
gemessen an der Entfernung Sonne - Sternhaufen.
• gleiche Materie – Zusammensetzung.
Alle Sternhaufen schildern allgemein die
„Lebensgeschichte“ eines Sterns in
Abhängigkeit von seiner Masse.
Allgemeinwissen
Kurt Grießer OStD i.R,
232
𝒓
𝒅
𝜶
= tan
𝟐
α≪𝟏
𝟐𝒓
𝒅
α
d
α/2
r
r
„Sternhaufen“
= tan α
Stern-Haufen
M44
M45
Melotte 25
Krebs
Plejaden
Hyaden
h + chi
Entfernung
Lj
515
444
153
6.800
α
´
110
330
30
Der Haufendurchmesser beträgt nur
2 – 3 % der Entfernung des Haufens.
Allgemeinwissen
Kurt Grießer OStD i.R,
D = 2r
Lj
13
14
15
59
2r/d
%
2,5%
3,2%
9,6%
0,9%
Die Haufenmitglieder haben
„gleiche“ Entfernung.
233
Allgemeinwissen
Kurt Grießer OStD i.R,
234
Stier
Hyaden
Allgemeinwissen
Kurt Grießer OStD i.R.
Astronom. Entfernungsmessungen
235
Hyaden - Eigenbewegungen
Nichtmitglieder
Guide 6
Kurt Grießer OStD i.R.
Astronom. Entfernungsmessungen
236
Hyaden
Allgemeinwissen
Kurt Grießer OStD i.R,
237
Plejaden
scheinbare Helligkeit
Entfernung der
Plejaden
„Sonne“ in den Plejaden:
T = 5800 K
mV = 10,4 mag
bekannt:
M = 4,8 mag
r = 𝟏𝟎
𝒎 −𝑴+𝟓
𝟓
pc
10,4 mag
r = 102,12 pc
r = 132 pc = 430 Lj
(Wikipedia: 134 pc)
Abitur By 1999
5.800 K
Kurt Grießer OStD i.R,
238
Plejaden - Hyaden scheinbare Helligkeiten
www3.kis.uni-freiburg.de
Kurt Grießer OStD i.R,
239
Entfernung einer
Sonne in den
Plejaden - Hyaden scheinbare Helligkeiten
Plejaden:
mV = 10,5 mag
Hyaden
mV = 8,0 mag
M = 4,8 mag
r = 𝟏𝟎
𝒎 −𝑴+𝟓
𝟓
_
pc
r = 138 pc = 450 Lj
(136)
(444)
r = 44 pc = 142 Lj
(47)
(152)
Farbindex der Sonne 0,65
www3.kis.uni-freiburg.de
Kurt Grießer OStD i.R,
240
Hauptreihenvergleich
(m – M)StH = (m – M)StH – Hyaden + (m – M)Hyaden

gesucht

HR– Vergleich

Parallaxen-Messung
M
2 gleiche Sterne 
= (Spektralklasse)
=
haben die gleiche
absolute Helligkeit M

Plejaden (139)
fornoff.homepage.t-online.de
Hyaden (44)

Kurt Grießer OStD i.R,
241
Entfernung aus Hauptreihenvergleich: Rechnung
absolute Entfernung eines Sternhaufens:
Entfernungsmodul (r in parsec;)
(m – M) = 5 lgr - 5;
r = 𝟏𝟎
𝒎 −𝑴+𝟓
𝟓
pc
(m – M)StH = (m – M)StH – Hyaden + (m – M)Hyaden
mit (m – M)StH – Hyaden = 2,5m
aus dem Diagramm
mit (m - M)Hyaden = 3.33m
(z. B. aus Parallaxenmessungen des Hipparcos-Satelliten
(m – M)StH = 2,5m + 3,3m = 5,8m
r = 144 pc = 471 Lj
Cambridge Enzyklopedie S.54
Kurt Grießer OStD i.R,
242
Hauptreihe in
scheinbarer
Helligkeit
fornoff.homepage.t-online.de
absoluter
Helligkeit
Kurt Grießer OStD i.R,
Hauptreihenvergleich
Entfernungsmodul
243
Alter und junger Sternhaufen
Die Abknickstelle von der Hauptreihe (Knie) ergibt mit der Theorie
der Sternentwicklung das Alter des Haufens
Millionen Jahre Verweilzeit
Milliarden Jahre Verweilzeit
SuW 2008/Heft 7
Kurt Grießer OStD i.R,
244
Alter und junger Sternhaufen
18
72
290
Millionen
Jahre
1,8
7,2
Milliarden
Jahre
29
720
SuW 2008/Heft 7
Kurt Grießer OStD i.R,
245
Offene Sternhaufen
M3
M 67
Cambridge Enzyklopedie S.54
Kurt Grießer OStD i.R,
248
academic.ru
Kurt Grießer OStD i.R,
249
6,5 x 106
2,8 x 107
1,6 x 108
1,2 x 109
M3
7,1 x 109
2,9 x 1010
Genähertes Alter des Abknickpunktes
2,0 x 106
Abknickstelle „Knie“ einiger Sternhaufen
Cambridge Enzyklopedie S.62
Kurt Grießer OStD i.R,
251
Junger Sternhaufen
2x106 Jahre
O, B – Sterne noch vorhanden
F, G, K, - Sterne noch nicht auf der
Hauptreihe
− 𝑬𝒎𝒊𝒔𝒔𝒊𝒐𝒏𝒔𝒍𝒊𝒏𝒊𝒆𝒏
/ veränderl. Sterne
ANHR: Alter-Null-Hauptreihe
Ambridge Enzyklopedrie S.63
Kurt Grießer OStD i.R,
254
THD
HRD
internet
Kurt Grießer OStD i.R,
257
THD
HRD
Abenteuer universum . de
Kurt Grießer OStD i.R,
258
scienceblogs.de
Kurt Grießer OStD i.R,
259
HRD
THD
internet
Kurt Grießer OStD i.R,
260
balkonsternwartennetzwerk.de
Kurt Grießer OStD i.R,
261
lexikon.astronomie.info/sterne/
hrd/
Kurt Grießer OStD i.R,
262
astro-rennes.com
Kurt Grießer OStD i.R,
263
O
B
A
F
G
K
M
R
N
O Be A Fine Girl Kiss Me Right Now
Offenbar Benutzen Astronomen
Furchtbar Gerne Komische Merksätze
Ohne Besondere Anstrengung Finde
Grüne Kleine Männchen
O
B
A
F
G
K
M
Ohne Bier Ausm Fass
Gibts Koa Mass
R
N
Aber noch besser:
Quelle
Kurt Grießer OStD i.R,
266
Ein Blick
zum Himmel
lohnt immer.
Herzlichen
Dank
fürs
Zuhören.
Einstein online
267
Auf folgende Themen wurden nicht oder nur kurz eingegangen:
Bolometrische Helligkeit
Einfluss der interstellaren Materie auf die scheinbaren Helligkeiten
eines Sterns.
Entwicklung eines Sterns und dessen Wege im HRD. (evtl. Folgevortrag).
Mathematische Voraussetzungen
(Zum Grundverständnis nicht unbedingt erforderlich)
Graphische Darstellung von Funktionen
Geradengleichung; einfache Umformungen in Gleichungen;
Logarithmische Rechengesetze
Physikalisch/astronomische Gesetzte:
Gravitationsgesetz, Stefan-Boltzmann; Temperaturskala Kelvin
Quelle
Kurt Grießer OStD i.R,
268
Antares

M 1 lb
M = - 4,8 mag
Sonne:

en.wikipedia.org
Kurt Grießer OStD i.R,
269
Literatur
Weigert/ Wendker:
Herrmann, Dietmar
Cambridge Enzyklopedie
Wischnewski
Astronomie und Astrophysik
Physik-Verlag, Weinheim
Arbeitsbuch Astrophysik
Books on demand, Norderstedt
Astronomie
Orbis Verlag
Astronomie in Theorie und Praxis
Selbstverlag
Kartunen/Kröger/Oja/
Poutanen/Donner
Astronomie - Eine Einführung
Springer-Lehrbuch
Unsöld / Baschek
Der neue Kosmos
Springer Verlag
Bergmann/Schäfer
Experimentalphysik Band 8
Sterne und Weltraum
W. de Gruyter
Kaler
Sterne und ihre Spektren
Spektrum Akademischer Verlag
Hinwiese in der Fußnote links unten
Internet unter einschlägigen Begriffen
Quelle
Kurt Grießer OStD i.R,
270
Literatur
Gondolatsch/Groschopf
SuW
A+R
Quelle
Astronomie I ; II ; III
Klettverlag
Zeitschrift Sterne und Weltraum
Teitschrift Astronomie und Raumfahrt
Kurt Grießer OStD i.R,
271