Abwärtswandler - Heinz Schmidt
Werbung

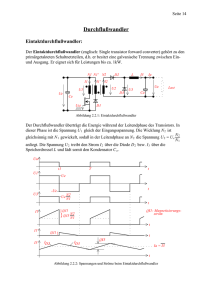
Seite 4 Abwärtswandler Der Abwärtswandler (englisch: buck-converter, step-down-converter) wandelt eine Eingangsspannung in eine niedrigere Ausgangsspannung. Er wird auch Tiefsetzsteller genannt. Ie T Ue IL Ust Ce D U1 L Ia UL Ua Last Ca Abbildung 1.1.1: Abwärtswandler Abbildung 1.1.1 zeigt das prinzipielle Schaltbild eines Abwärtswandlers. Der Transistor T arbeitet als Schalter, der mittels der pulsweiten-modulierten Steuerspannung U St mit hoher Frequenz ein- und ausgeschaltet wird. Der Quotient zwischen Einschaltzeit zu Periodendauer t1 heißt Tastverhältnis oder Tastgrad (englisch: duty cycle). T Ust t1 U1 t T Ue Ua = U1 t UL (Ue-Ua) t -Ua IL ∆ IL Ia = I L t Abbildung 1.1.2: Spannungen und Ströme beim Abwaärtswandler Für die folgende Funktionsbeschreibung der Schaltung sei vereinfachend angenommen, daß der Transistor und die Diode keinen Spannungsabfall während der jeweiligen Einschaltphasen haben. Während der Einschaltphase des Transistors ist die Spannung U 1 gleich U e . Während seiner Sperrphase zieht die Induktivität L ihren Strom durch die Diode und die Spannung U 1 wird somit zu Null. Vorraussetzung dafür ist, daß der Strom I L nie Null wird. Diesen Betriebsfall nennt man kontinuierlicher Betrieb bzw. nicht lückender Betrieb (englisch: continous mode). U 1 ist demnach eine Spannung, die zwischen U e und Null Volt entsprechend dem Tastverhältnis von U st springt, siehe Abbildung 1.1.2. Der nachfolgende Tiefpaß, gebildet aus L und C a , bildet den Mittelwert von U 1 . Damit ist U a = U 1 , bzw es gilt Seite 5 für den kontinuierlichen Betrieb: Ua = t1 Ue T Die Ausgangsspannung ist im kontinuierlichen Betrieb nur vom Tastverhältnis und der Eingangsspannung abhängig, sie ist lastunabhängig. Der Strom I L hat dreieckförmigen Verlauf. Sein Mittelwert ist durch die Last bestimmt. Seine Welligkeit ∆I L ist von L abhängig und kann mit Hilfe des Induktionsgesetzes berechnet werden: u = L di t Mit U a = → ∆i = 1 ⋅ u ⋅ ∆t L → ∆I L = 1 (U e − U a ) ⋅ t 1 = 1 U a (T − t 1 ) L L t1 U e und einer gewählten Schaltfrequenz f folgt daraus für den kontinuierlichen T Betrieb: U ∆I L = 1 (U e − U a ) ⋅ a ⋅ 1 L Ue f Die Stromwelligkeit ∆I L ist lastunabhängig. Der Mittelwert des Stromes I L ist gleich dem Ausgangsstrom I a . ∆I L ist, wird der Strom I L in jeder Periode zu 2 Null. Man nennt dies den lückenden Betrieb bzw. diskontinuierlichen Betrieb (englisch: discontinous mode). In diesem Falle gelten die oben angegebenen Berechnungen nicht mehr. Bei kleinem Laststrom I a , nämlich wenn Ia ≤ Berechnung von L und Ca : Für die Berechnung von L wird zunächst ein sinnvoller Wert für ∆I L gewählt. Wählt man ∆I L sehr klein, so führt das zu unverhältnismäßig großen Induktivitätswerten. Wählt man ∆I L sehr groß, so wird der zum Zeitpunkt t 1 vom Transistor abzuschaltende Strom sehr groß, d.h. der Transistor wird hoch belastet. Üblich ist daher die Wahl: ∆I L = 0, 1…0, 2 ⋅ I a damit folgt für L : U L = 1 (U e − U a ) ⋅ a ⋅ 1 ∆I L Ue f Der Maximalwert des Induktivitätsstromes beträgt: I L = I a + 12 ∆I L . I Leff ≈ I a Der Effektivwert beträgt näherungsweise: Den Ausgangskondensator C a wählt man so, daß die Grenzfrequenz des LC -Tiefpasses um den Faktor 100...1000 unterhalb der Taktfrequenz liegt. Eine genaue Bestimmung des Seite 6 Kondensators hängt von seiner Wechselstrombelastbarkeit und seine Serienersatzimpedanz Z max ab (beides kann dem entsprechenden Datenblatt entnommen werden). Die Welligkeit ∆I L verursacht am Ausgangskondensator eine Spannungswelligkeit ∆U a . Diese ist bei dem hier relevanten Frequenzbereich maßgeblich bestimmt durch die resultierende Impedanz des Ausgangskondensators: ∆U a ≈ ∆I L ⋅ Z max Die Wahl des Ausgangskondensators richtet sich also nach der Impedanz Z max des Kondensators. Z max kann dem Datenblatt des Ausgangskondensators entnommen werden.